정수론

07-3 유클리드 호제법

유클리드 호제법(euclidean-algorithm)은 두 수의 최대 공약수를 구하는 알고리즘이다. 일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수들의 곱으로 표현할 수 있지만 유클리드 호제법은 좀 더 간단한 방법을 제시한다.

유클리드 호제법의 핵심이론

유클리드 호제법을 수행하려면 먼저 MOD 연산을 이해하고 있어야 한다. MOD 연산이 최대 공약수를 구하는 데 사용하는 핵심 연산이기 때문이다.

연산	기능	예제
MOD	두 값을 나눈 나머지를 구하는 연산	10 MOD 4 = 2

MOD 연산으로 구현하는 유클리드 호제법

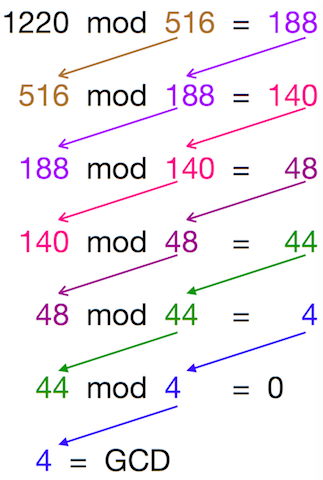
1. 큰 수를 작은 수로 나누는 MOD 연산을 수행한다.
2. 앞 단계에서의 작은 수와 MOD 연산 결괏값(나머지)으로 MOD 연산을 수행한다.
3. 단계 2를 반복하다가 나머지가 0이 되는 수간의 작은 수를 최대 공약수로 선택한다

이 과정은 재귀함수로써 표현이 가능하다.

---

문제 042 최소 공배수 구하기

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
1 초	128 MB	66942	36887	31446	56.302%

문제
두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있으며, 최소 공배수는 30이다.

두 자연수 A와 B가 주어졌을 때, A와 B의 최소공배수를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 1,000)가 주어진다. 둘째 줄부터 T개의 줄에 걸쳐서 A와 B가 주어진다. (1 ≤ A, B ≤ 45,000)

출력
첫째 줄부터 T개의 줄에 A와 B의 최소공배수를 입력받은 순서대로 한 줄에 하나씩 출력한다.

예제 입력 1
3
1 45000
6 10
13 17

예제 출력 1
45000
30
221

---

이 문제를 정석대로 풀면 시간 복잡도는 O(N2)으로 시간 초과가 나면서 풀 수 없게 된다. 따라서 유클리드 호제법으로 문제를 풀어야 하는데 최소 공배수는 A와 B가 주어졌을 때 'A * B / 최대 공약수'를 계산해 구할 수 있다. 그래서 이 문제는 유클리드 호제법을 이용해 최대 공약수를 구한 후 두 수의 곱에서 최대 공약수를 나눠 주는 것으로 해결할 수 있다.

import sys
sys.stdin = open("input.txt", 'rt')

def DFS(l, s):
    if s == 0:
        return l
    else:
        return DFS(s, l%s)

T = int(input())
for _ in range(T):
    a, b = map(int, input().split())
    l = max(a, b)
    s = min(a, b)
    ans = a * b / DFS(l, s)
    print(int(ans))

이 코드에서 주목할 점은 재귀함수 부분이다. 그 동안 봐왔던 재귀함수와는 달리 이 경우 return이 if와 else에 둘 다 달려있다. 재귀 함수의 경우 보통 스택 구조를 이용한다. else 부분에 return을 달지 않으면 재귀함수는 결국 다시 돌아가 처음에 넣었던 l 값을 return하게 된다. 그걸 막기 위해서 else 부분에도 return을 넣어주는 것이다.

07-4 확장 유클리드 호제법

유클리드 호제법의 목적이 두 수의 최대 공약수를 구하는 것이라면 확장 유클리드 호제법의 목적은 방정식의 해를 구하는 것이다. 확장 유클리드 호제법은 어느 정도 지엽적인 부분이 있다고 판단하여 일단은 내용만 간단하게 알아보고 넘어가도록 하자.

확장 유클리드 호제법의 핵심 이론

확장 유클리드 호제법에서 해를 구하고자 하는 방정식은 다음과 같다.

ax + by = c (a, b, c, x, y는 정수)

이때 위 방정식은 c % gcd(a, b) = 0인 경우에만 정수해를 가진다. 다시 말해 c와 a와 b의 최대 공약수의 배수인 경우에만 정수래를 가진다. 이는 ax + by = c가 정수해를 갖게 하는 c의 최솟값이 gcd(a, b)라는 것을 의미한다. 이 내용을 숙지한 후 확장 유클리드 호제법을 구현하자. 구현에는 재귀 함수를 사용한다.

확장 유클리드 호제법의 원리 이해하기

5x + 9y = 2일 때 이 식을 만족하는 정수 x, y 값을 구해 보자.

1. 우선 5x + 9y가 정수해를 갖게 하는 c의 최솟값이 gcd(5, 9)라는 것을 적용하여 식을 다시 놓는다. gcd(5, 9) = 1이므로 5x + 9y = 1로 식을 다시 놓고 다음 단계를 진행한다.

2. a, b로 유클리드 호제법을 반복 실행하며 몫, 나머지를 저장한다. 반복은 나머지가 0이 되면 중단한다.

유클리드 호제법 실행	나머지	몫
5 % 9 = 5	5	0
9 % 5 = 4	4	1
5 % 4 = 1	1	1
4 % 1 = 0	0	4

3. 반복으로 구한 나머지와 몫을 이용하여 거꾸로 올라가며 x = y', y = x' - y' * q를 계산한다. x'는 이전 x, y'는 이전 y를 의미하고, q는 현재 보고 있는 몫을 의미한다. 이때 처음 시작하는 x, y는 이전 x와 이전 y가 없으므로 각각 1, 0으로 지정하여 역계산을 진행한다.(밑에서 위로 진행)

x=y', y=x'-y'*q 역순 계산	나머지	몫
X =2, Y = -1-(2*0)=-1	5	0
X =-1, Y = 1-(-1*1)=2	4	1
X =1, Y = 0-(1*1)=-1	1	1
X =0, Y = 1-(0*4)=1	0	4

4. 이렇게 재귀 방식으로 알아낸 최종 x, y는 ax + by = gcd(a, b)를 만족한다. 그리고 c / gcd(a, b) = K를 가정하면 최초 방정식의 해는 Kx, Ky로 간단히 구할 수 있다. 과정 3에서 찾은 x는 2, y는 -1이고 K값을 구하면 2(c값) / 1(최대 공약수) = 2가 되므로 2의 값을 기존의 x(2), y(-1) 값에 각각 곱한다. 이에 따라 최초 방정식의 해는 4, -2가 된다.