그래프

08-2 유니온 파인드

유니온 파인드는 일반적으로 여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union 연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성되어 있는 알고리즘이다.(유니온 + 파인드)

유니온 파인드의 핵심 이론

유니온 파인드는 union, find 연산을 완벽히 이해하는것이 핵심이다.

union, find 연산

• union 연산: 각 노드가 속한 집합을 1개로 합치는 연산이다. 노드 a, b가 $a \in A$, $b \in B$일 때 union(a, b)는 $A \cup B$를 말한다.
  
  
• find 연산: 특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산이다. 노드 a가 $a \in A$일 때 find(a)는 A 집합의 대표 노드를 반환 한다.

유니온 파인드의 원리 이해하기

두 연산을 알아봤으므로 이번에는 유니온 파인드 알고리즘 구현 방법을 알아보자.

1. 유니온 파인드를 표현하는 일반적인 방법은 1차원 리스트를 이용하는 것이다. 처음에는 노드가 연결되어 있지 않으므로 각 노드가 대표 노드가 된다. 각 노드가 모두 대표 노드이므로 리스트는 자신의 인덱스값으로 초기화 된다.

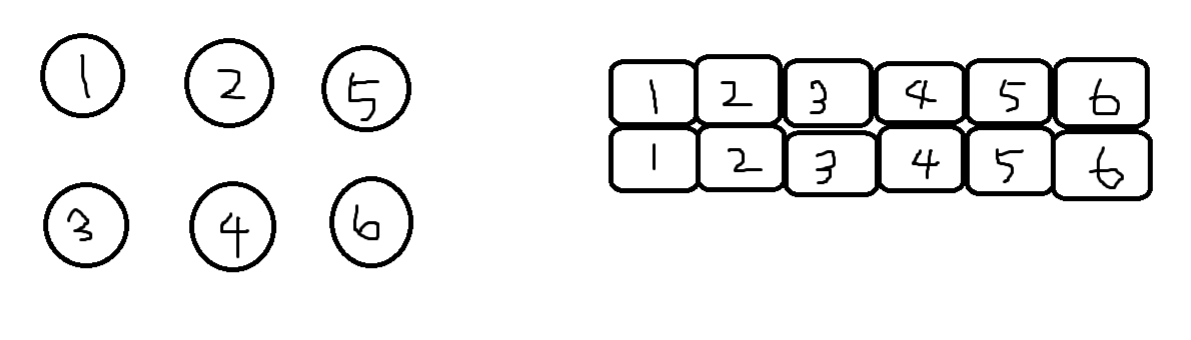
2. 2개의 노드를 선택해 각각의 대표 노드를 찾아 연결하는 union 연산을 수행한다. 리스트를 보면 1, 4와 5, 6을 union 연산으로 연결한다. 리스트[4]는 1로, 리스트[6]은 5로 업데이트 한다. 이렇게 업데이트하는 것의 의미를 이해해야 한다. 1, 4의 연결을 예를 들면 1은 대표 노드, 4는 자식 노드로 union 연산을 하므로 리스트[4]의 대표 노드를 1로 설정한 것이다. 다시 말해 자식 노드로 들어가는 노드값 4를 대표 노드값 1로 변경한 것이다. 그 결과 각각의 집합이었던 1, 4는 하나로 합쳐진다.

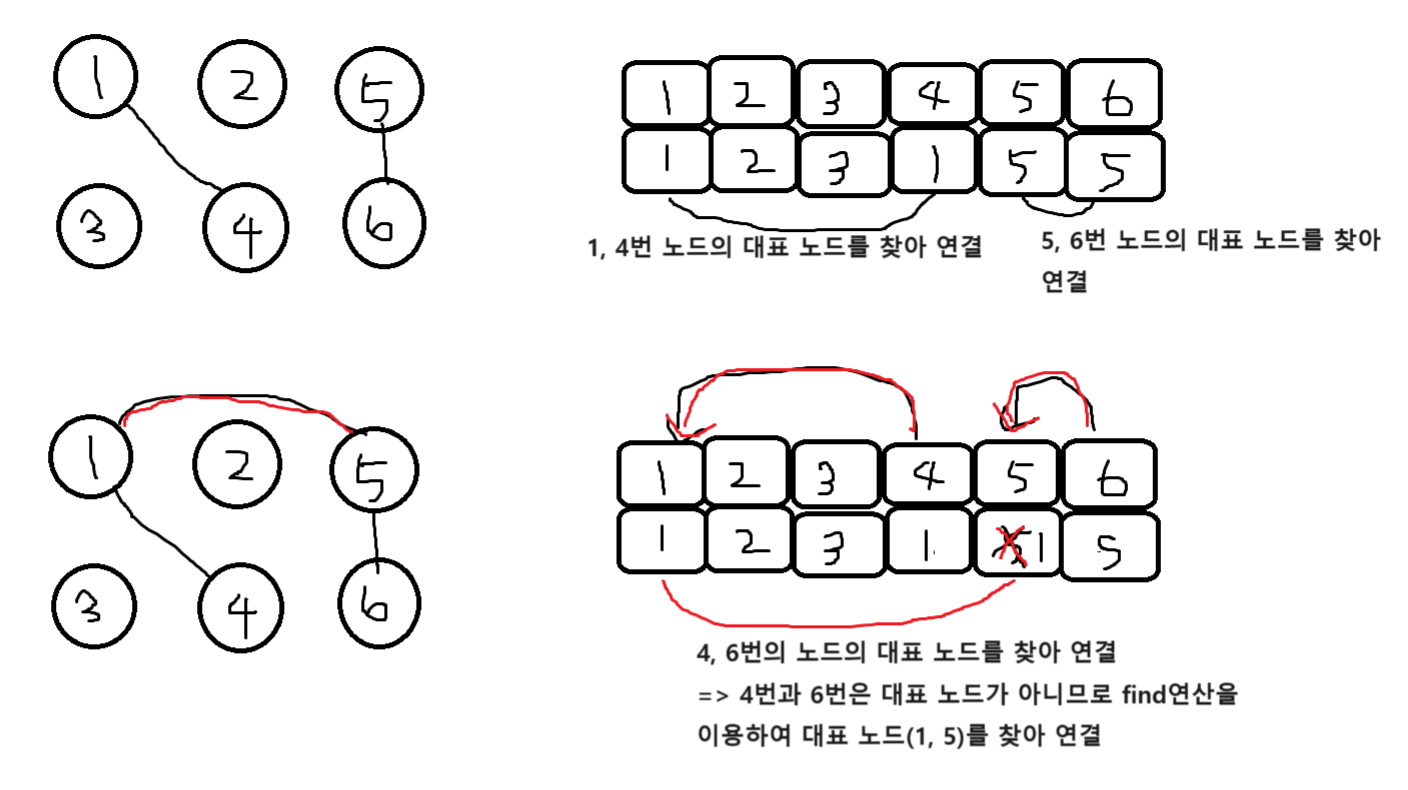
이제 union(4, 6)으로 4와 6을 연결해보자. 그런데 4, 6은 대표 노드가 아니다. 그래서 각 노드의 대표 노드를 찾아 올라간 다음 그 대표 노드를 연결한다. 지금의 경우 4의 대표 노드 1에 6의 대표 노드 5를 연결한 것이다. 리스트는 그럼 [1, 2, 3, 1, 1, 5]가 된다. 리스트 상태로 보면 그래프의 연결이 잘 안 보일 수도 있겠지만 다음 find 연산 설명을 보면 위 리스트가 그래프 연결을 잘 나타내고 있다는 것을 알 수 있다.

3. find 연산은 자신이 속한 집합의 대표 노드를 찾는 연산이다. find 연산은 단순히 대표 노드를 찾는 역할만 하는 것이 아니라 그래프를 정돈하고 시간 복잡도를 줄인다.

• find 연산의 작동원리

1. 대상 노드 리스트에 index 값과 value 값이 동일한지 확인한다.
2. 동일하지 않으면 value값이 가리키는 index 위치로 이동한다.
3. 이동 위치의 index값과 value값이 같을 때까지 1~2를 반복한다. 반복이므로 이 부분은 재귀 함수로 구현한다.
4. 대표 노드에 도달하면 재귀 함수를 빠져나오면서 거치는 모든 노드 값을 대표 노드값으로 변경한다.

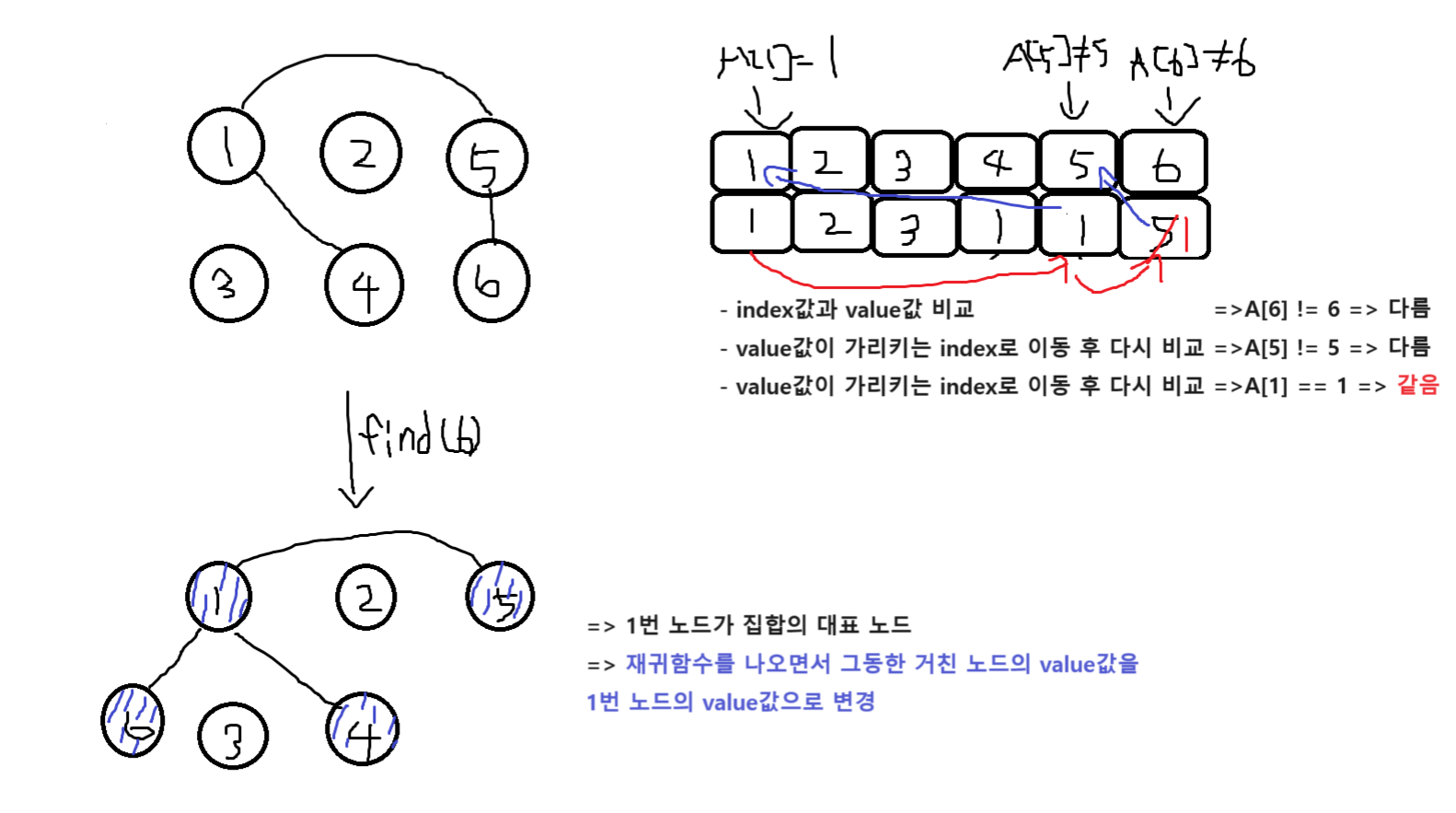
find 연산은 잘 생각하면 시간 복잡도가 줄어드는 효과를 얻게 된다. 연산을 할 때 거치는 노드들이 대표 노드와 바로 연결되는 형태로 변경되기 때문이다. 이렇게 되면 추후 노드와 관련된 find 연산 속도가 O(1)로 변경된다.

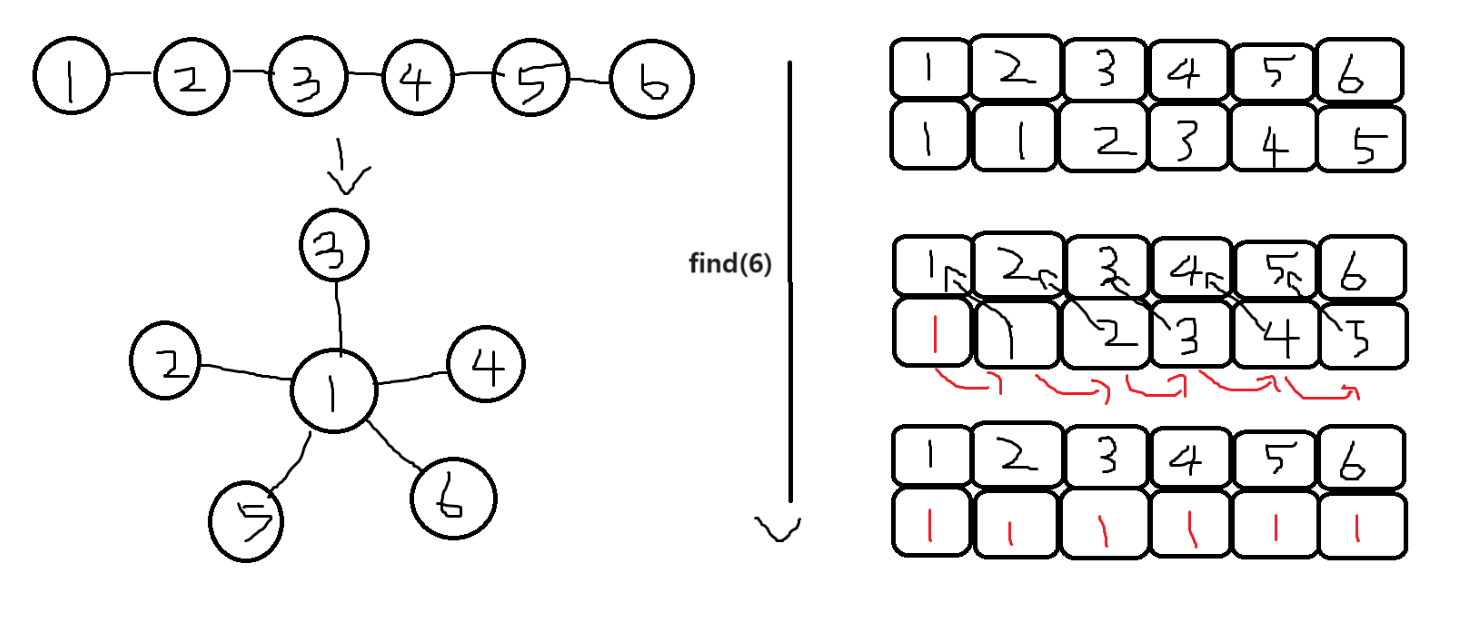
한 번의 find 연산을 이용해 모든 노드가 루트 노드에 직접 연결되는 형태로 변경되는 것을 볼 수 있다. 이러한 형태로 변경되면 이후 find 연산이 진행될 때 경로 압축의 효과가 나타난다. 예를 들어 이후 find(4) 연산을 수행하면 한 번의 이동으로 바로 대표 노드를 찾을 수 있다.

경로 압축은 실제 그래프에서 여러 노드를 거쳐야 하는 경로에서 그래프를 변형해 더 짧은 경로로 갈 수 있도록 함으로써 시간 복잡도를 효과적으로 줄이는 방법을 말한다.