*이미지를 클릭 시 출처로 이동
- 머신러닝 기법은 원레 시계열 데이터에 특화되어 개발된 것이 아니지만 시계열에서도 유용한 성능을 발휘함
- arima모델처럼 '시간을 인식'하는 방법론이 아니기 때문에 시계열의 특징을 생성하는 것이 트리기반 방법론에서 반드시 필요함.
- 클러스터링 및 거리 기반의 분류는 입력으로 원본 시계열이나 특징을 사용할 수 있음. 시계열 자체를 입력으로 사용하려면
동적시간워핑(DTW)이라는 거리 평가지표를 알아야 함. - DTW는 데이터 전체에 대한 시간 정보를 보존함.
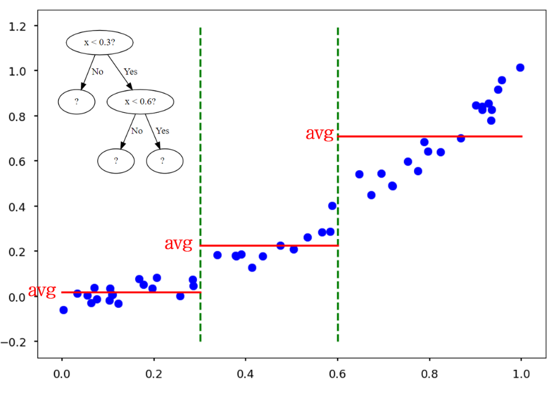
9.1.2 결정트리 기법
랜덤포레스트
- 여러 개의 결정트리 모델이 도출한 결과값의 평균
- 한 개의 최고 모델이 아닌 여러 모델을 앙상블하여 예측한다는 개념
- 원시 데이터의 시계열 특징을 압축&요약하면 유용할 수 있음
- 보통 랜덤포레스트는 배깅방법으로 학습
그래디언트 부스팅 트리
-
모델이 스스로 관련성이 적거나 노이즈가 많은 특징은 제거하고 중요한 특징에 초점을 맞춤.
-
(모델선택보다 중요한 것은 고품질 입력데이터임)
-
일반적으로 시계열 예측보다 분류에서 유용한 랜덤포레스트와 달리 예측, 분류 모두 우수한 성능을 보임
-
boosting : 이전 모델에서 잘못 적합된 데이터는 이후 모델에서 더 큰 가중치를 가짐
-
XGBoost: 모델의 복잡도에 대한 패널티항을 포함한 손실함수 최소화.
-
그래디언트 부스팅 트리는 대규모 시계열 데이터셋을 포함한 대규모 데이터셋에서 특히 유용함.
-
XGBoost 외에 LightGBM과 CatBoost 라이브러리의 사용도 고려해야 함.
-
LightGBM, CatBoost의 경우 낮은 정확도를 보일 때도 있으나 보통 XGBoost보다 빠름.
Bagging VS Boosting
| Bagging | Boosting | |
|---|---|---|
| 특징 | 병렬적(각모델이 독립적) | 순차적(이전 모델의 오류 고려) |
| 목적 | Variance 감소 | Bias 감소 |
| 대표 알고리즘 | RandomForest | Gradient Boosting, AdaBoost |
GradientBoosting vs AdaBoost vs XGBoost vs CatBoost vs LightGBM
알고리즘 유형 장점 단점 RandomForest 배깅 높은 정확도, 과적합 방지, 특성 중요도 제공 예측 속도가 부스팅 모델보다 느릴 수 있음, 많은 메모리 사용 Gradient Boosting 부스팅 높은 예측 정확도, 다양한 손실 함수 지원 매개변수 조정 필요, 비교적 학습 시간이 길 수 있음 AdaBoost 부스팅 단순하고 구현하기 쉬움, 이진 분류에 강력 노이즈와 이상치에 취약 XGBoost 부스팅 병렬 처리 지원, 높은 정확도, 과적합 방지 기능 제공 매개변수 조정 필요, 메모리 사용량이 높을 수 있음 CatBoost 부스팅 범주형 데이터 처리 우수, 빠른 학습 및 예측 속도 매개변수 조정이 비교적 복잡할 수 있음 LightGBM 부스팅 빠른 학습 및 예측, 적은 메모리 사용, 대용량 데이터 처리 가능 작은 데이터셋에서 과적합 위험 구현 알고리즘
|알고리즘 |유형| 특징|
|Gradient Boosting|부스팅 |잔차(실제값-예측값)릍 최소화하는 방식으로 학습. 잔차 최소화를 위해 경사하강법 사용. |
|AdaBoost |부스팅 | Adaptive Boosting. |
|XGBoost |부스팅 |eXtreme Gradient Boosting. 병렬 처리 지원, 높은 정확도, 과적합 방지 기능 제공. Gradient Boosting모델과 베이스는 동일하나 generalization error를 줄이기 위해 벌점항 추가|
|CatBoost |부스팅 |Category Boosting. 대칭 트리를 사용하고 범주형 기능을 직접 처리하여 그라데이션 부스팅 프로세스를 최적화|
|LightGBM| 부스팅|Light Gradient Boosting Model. 일반적인 level-wise 방식이 아닌 leaf-wise(특정 가지만 깊게)로 XGBoost보다 시간 단축 효과. 따라서 데이터 적은 경우 과대적합 위험성|
트리모델로 분류모델과 회귀모델 구현하기
- Classification Tree
- 이산형 레이블의 예측이 목표
- 분기기준이 Entropy, Gini index등이 됨
- 각 결정트리가 데이터 포인트를 특정 클래스에 속하게 하고 가장 많은 트리가 선택한 클래스를 최종 예측값으로 선택
- Regression Tree
- 연속형 레이블의 예측이 목표
- 분기 기준을 실제값과 예측값의 차이(=오차) 사용
- 각 결정 트리가 예측한 값의 평균을 취해 최종 예측값 결정
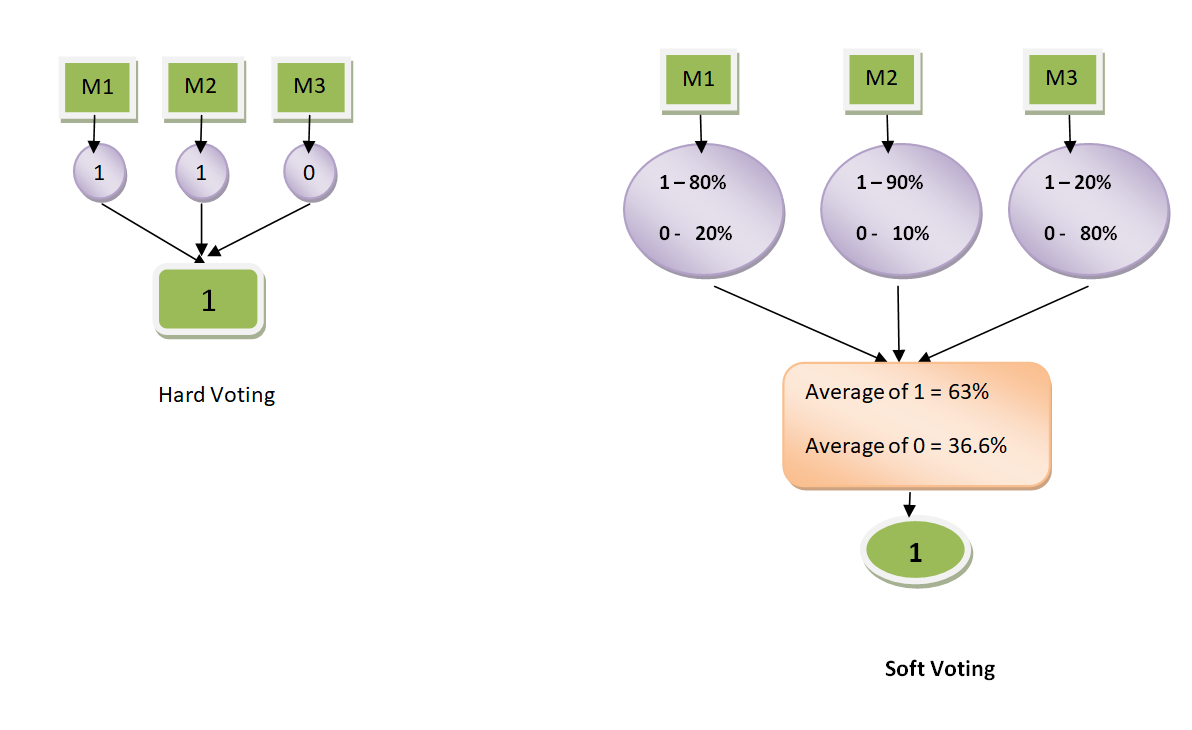
❗SoftVoting VS HardVoting
- Hard Voting : 결과값에 대한 다수결
- Soft Voting : 결과값의 '확률'의 평균의 크기 비교
9.2 클러스터링
-
분석의 목적상 서로 유사한 데이터가 의미 있는 집단을 구성한다는 것이 클러스터링의 기본 개념
-
시계열에서의 클러스터링은 분류와 예측 모두에서 사용될 수 있음.
-
분류의 경우 클러스터링 알고리즘을 이용하면 원하는 수만큼의 집단을 모델의 학습 단계에서 식별할 수 있음. 그리고 식별된 집단을 이용해 시계열의 범주를 규명하고, 새로운 샘플이 소속될 집단을 인식할 수 있음
-
예측에서는 순수 클러스터링이나 거리 측정법을 이용하는 형태의 클러스터링이 사용될 수 있음.
1) 특정 행동에 기반한 예측을 생성하기 위해 그 행동을 규정하는 규칙을 사용.
해당 클러스터의 시계열값들이 가는 시간 단계 N과 N+h 사이에서 변화하는 방식을 살펴보는 것.
사전 관찰의 발생을 피하기 위해 시계열의 모든 부분이 아니라 처음 N개의 단계에만 기반해 클러스터링을 수행해야 함.
2) 표본 시계열의 미래 행동을 표본 공간의 최근접이웃의 행동에 기반해 예측 -
처음 n개의 시간 단계에 대한 지표에 기반해 해당 시계열의 최근접 이웃을 찾고 이 최근접 이웃들의 N+h 행동의 평균을 구하면 현재 표본에 대한 예측을 얻게 됨.
-
분류와 예측 모두 시계열 간의 유사성을 평가하는 방법이 가장 중요한 고려사항임.
-
유사성을 측정가능한 지표로 변환하면 '거리' 개념이 됨.
거리측정법
1) 특징 기반
2) 원시 시계열 데이터 기반
9.2.2 시간을 인식하는 거리 측정법
- 시계열 간의 유사성 측정 문제를 다루기 위한 거리 지표 정의
EX) DTW,프레셰거리, 피어슨 상관, 최장공통부분 수열
특징 기반 vs DTW 기반
- DTW기반 클러스터링의 성능이 우수함.
- 그러나 DTW거리계산의 경우 시간이 오래걸리고 추후 그 이상의 개선 여지가 없음.
