[논문리뷰] Solving Quantitative Reasoning Problems with Language Models : Minerva

jihwanyoon·2023년 1월 31일
LanguageModelNLPPLMPaLMgoogle논문리뷰
0

Paper Reviews

목록 보기
1/9

1. Introduction

  • 다양한 자연어 task에서 성공을 거둔 거대 언어 모델.
  • 하지만 양적 추론(quantitative reasoning)이 필요한 task에서 고전하였다. ex) 수학, 과학, 공학 문제들…

💡 Quantitative Reasoning
여러 방면에서 모델의 능력을 시험할 수 있는 흥미로운 도메인이다. 자연어 input을 올바르게 구문 분석하고 계산하여 과학이나 engineering 분야에서 인간의 작업을 지원하는 유용하게 사용된다.

  • 이전 연구에서 거대 언어 모델이 도메인 특화된 데이터셋을 학습한 후 수학 및 프로그래밍 질문들에서 좋은 성능을 달성하였음을 보였다.

=⇒ 저자들은 이를 외부 도구에 의존하지 않으며 완전하고 자체적인 솔루션을 제공하는 양적 추론 문제에 적용하였다.

1.1 Our Contribution

💡 Minerva

  • 많은 quantitative reasoning 작업에서 강력한 성능을 달성한 언어 모델.
  • 자연어로 공식화된 과학 및 수학적 질문을 처리, LATEX 표기법을 사용하여 단계별 솔루션을 생성할 수 있음.
  • PaLM(Pathway Language Model)을 기반으로 고품질의 과학, 수학 데이터셋을 학습시킴.
  • model size : 8B, 62B, 540B
  • MATH, GSM8k, MMLU-STEM에서 SOTA 달성.
  • 평가 데이터셋에 대해 few-shot setting 만으로 robust한 성능을 보인다.
  • 사용한 데이터셋은 arXiv preprint server와 웹페이지들에서 수학자료들의 loss를 minimise 하기 위해 세밀히 가공하여 모았다.

=⇒ 이에 SOTA 달성 뿐만 아니라 데이터 품질과 모델사이즈를 늘림으로써 Quantitative reasoning 벤치마크의 새로운 베이스라인을 세웠다.

  • 벤치마크 적용 범위 증대를 위해 MIT의 OCW(OpenCourseWare)에서 200개 이상의 과학 및 수학 학부 수준의 질문 데이터 세트를 구축하였다.

  • GSM8k Cobbe et al. (2021)는 verifiers들이 모델 output의 순위를 다시 매기게 훈련시킴으로서 성능향상이 됨을 보였다. (본 논문에선 외부 도구를 쓰지 않는 self-contained model에 집중한다.)

💡 기존 생성 task에서 language model을 평가하는 방법

1) 표준 방법은 문제 당 하나를 sampling 하는 것
2) 최근 연구들에선 문제 당 여러 solution들을 sampling하고 최종 답을 filtering하는 것은 너무 도전적이라는 것을 밝혀냈다. (Chen et al., 2021; Li et al., 2022; Thoppilan et al., 2022; Wang et al., 2022)

  • 본 논문에선 majority voting(Wang et al., 2022)가 greedy decoding에 비해 상당한 성능 향상을 보임을 발견하였다.

Code generation

  • PaLM(Chowdhery et al., 2022) 는 훈련 데이터셋에 코드를 포함하고 있는 거대 언어모델은 GSM8k의 코드 버전에서 좋은 성능을 보인다고 한다.
  • Codex model(Chen et al., 2021)은 MATH 문제들의 코드 솔루션을 생성해냈다고 한다.

Formal mathematics

  • 수학은 자연어를 기반으로 한 학문으로 발전했지만 그것의 공리적인 기초는 수학적 사고의 시뮬레이션을 가능케 한다.(???)
  • 이는 컴퓨터를 이용한 논리적, 수학적 사고의 시뮬레이션을 용이하게 하는 전문 프로그래밍 언어를 사용하여 달성 가능하다.
  • E (Schulz, 2013), leanCoP (Otten, 2008), and Vampire (Kovács and Voronkov, 2013) 와 같은 자동화된 증명 보조장치들이 기계학습과 결합되어 상당한 혜택을 받았다.

Language models applied to formal and synthetic mathematical problems

  • 이전엔 수학적 표현을 예측하기 위해 언어 모델을 훈련시켰다고 한다.
    (Rabe et al. (2021); Li et al. (2021); Polu and Sutskever (2020); Wu et al. (2021); Han et al. (2022); Polu et al. (2022); Jiang et al. (2022); Wu et al. (2022))
  • fomal language의 경우 여전히 GNN과 같이 주어진 수학공식 그래프 구조에 대한 정보를 쉽게 유지하는 모델들은 경쟁력있다고 한다.

Modelling mathematics as a discipline of natural language

  • 새로운 벤치마크 데이터셋(Hendrycks et al., 2021; Welleck et al., 2021)은 더 고급수학 주제를 다루지만 이 도메인에서 여전히 다른 클래스의 모델들과 경쟁하기엔 제한된다.

2. Training and Evaluation

2.1 Mathematical Training Dataset

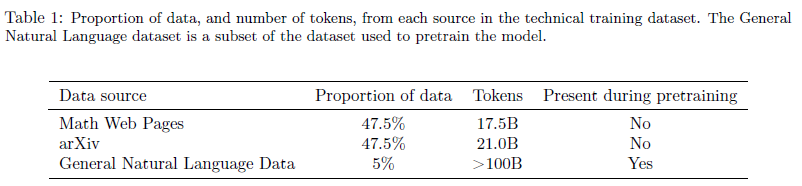
  • 수학 내용으로 필터링된 웹페이지와 arXiv에 등록된 논문의 38.5B 토큰 분량의 데이터셋(MathJax format, 대부분의 HTML tag 제거, LATEX symbol과 format과 같은 수학적 표기법은 보존하는 cleaning 과정을 거쳤다.)
  • PaLM을 사전 학습시키기 위해 사용된 일반적인 자연어 데이터셋
  • 이를 통해 계산 및 기호 조작이 필요한 작업에서 모델이 잘 작동하게 만들었다.

2.2 Models and Training Procedure

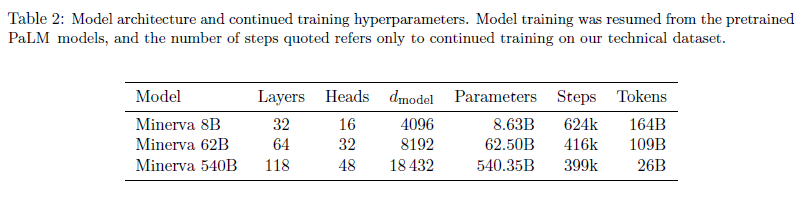
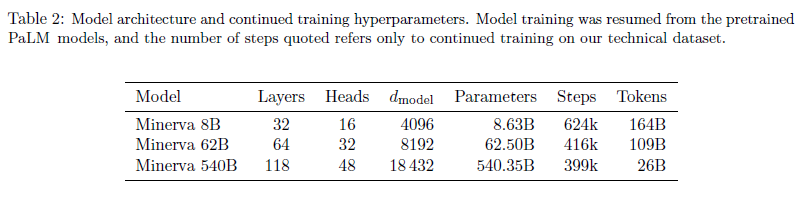
  • 사전학습된 PaLM을 autoregressive objective를 이용하여 수학 데이터셋에 fine-tuning 시킨다.
  • 540B 모델은 26B 토큰으로 fine-tuning시키는데 이는 8B, 62B에 비해 상당히 덜 학습시키지만 여전히 상당한 성능을 기록한다.

💡 Details
- context length : 2,048
- batch size : 128(except for the 540B model : 32)
- learning rate schedule : reciprocal square-root decay
- training steps
⇒ 8B : 1M steps + 600k additional unsupervised finetuning steps
⇒ 62B : 520k steps + 400k additional unsupervised finetuning steps
⇒ 540B : 257k steps + 383k additional unsupervised finetuning steps
- learning rate was dropped 10x and all models were then trained for 4% additional steps
*- t5x framework(Roberts et al., 2022)*

  • v4 TPU on Google Cloud
    - training time
    ⇒ 8B : 14 days on a v4-128
    ⇒ 62B : 17 days on a v4-512
    ⇒ 540B : 29 days on a v4-1024**

2.3 Evaluation Datasets

  • few-shot evaluation을 main focus로 잡는다.
  • input을 왼쪽에서 1024 token을 기준으로 자르고 512 token 까지 생성한다.
  • 한 문제당 하나를 할 경우 greedy sampling, 두 개 이상일 경우 T=0.6, p=0.95인 nucleus sampling(Holtzman et al., 2019)을 한다.
  • 생성 task의 경우 모델은 chain-of-thought 답을 생성하고 최종 답을 구분한다. 만약 답이 맞으면 chain-of-thought의 품질에 관계없이 맞은 것으로 한다.
  • 정확성 평가를 위해 최종 답을 구문 분석하고 SymPy 라이브러리르 이용해 비교한다. 이는 수학적으로 같은 경우를 식별하기 위해서이다.

MATH

  • LATEX 구문으로 쓰여진 12k의 중,고등학생 수학문제 데이터셋(Hendrycks et al. (2021))

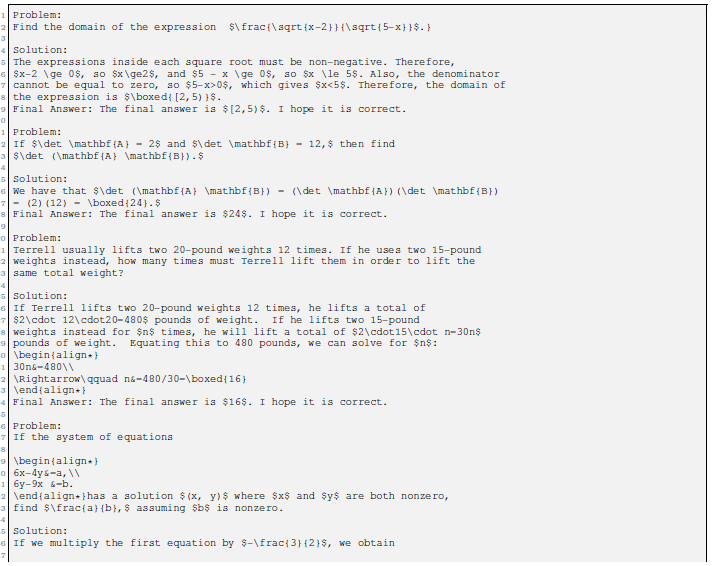
  • 훈련셋에서 정답이 길지 않은 4개의 고정된 prompt를 모델에 사용하였다.

💡 few-shot learning 용어 간단정리

way : 데이터 클래스의 개수  (ex. 개고양이 분류기 - 2 way classification)

shot, point : 데이터의 개수

query : test data (엄연히 따지자면 validation data)

source : train data

출처 : https://huidea.tistory.com/252?category=879542

GSM8k

  • 중학교 수학단어 문제(Cobbe et al. (2021)
  • chain-of-thought prompt를 이용하여 평가하였다.
  • 기존의 모델들은 외부 계산기를 활용하였으나 본 논문에선 외부 도구를 사용하지 않았다.

MMLU-STEM

  • MMLU dataset에서 science, technology, engineering, mathematics(STEM)에 집중한 데이터셋이다.
  • 5-shot prompt + chain-of-thought prompting(examples that include step-by-step solutions)

Prompt Tuning??

2.4 Undergraduate-Level STEM Problems

  • MIT(OpenCourseWare)의 publicly-available course meterials 에서 automatically-verifiable solutions(SymPy)을 통해 수집한 학부 수준의 데이터셋.
  • 대부분이 multi-step reasoning을 포함하며 본 논문에선 OCWCourses 라고 부른다.

2.5 Inference-Time Techniques

  • greedy decoding을 능가할 방법으로 k>1 개의 solutions들을 sampling하고 하나를 majority voting( Wang et al. (2022))로 뽑는 방법을 찾아냈다.

⇒ 최종 답변에 대한 예측을 그룹화하고 가장 일반적인 답변을 선택하는 방법 : maj1@k

  • majn@k : 위의 확장 버전, n개의 가장 일반적인 답변 선택하기.
  • 직관적으로, majority voting이 성능을 향상시키는 이유가 답변을 잘못하는 경우는 많은 반면에 정확하게 답변하는 경우는 매우 적기 때문이라고 한다.

💡 pass@k :
k개의 출력 중 하나 이상이 모든 단위 테스트를 통과하면 문제가 해결된 것으로 간주하고 그 비율을 측정한 평가 지표.

  • 평가 지표마다 얼마나 k에 의존하는지에 대해 실험

    • pass@k는 k가 커질수록 증가한다. 분포의 꼬리에서 성능 향상이 이루어진다.

    • 위와 반대로, majority voting 성능은 더 빠르게 포화된다. 97% 정확도 달성까지 MATH는 k=64, GSM8k는 k=16

      ⇒ 가장 일반적인 답을 고르고 k가 클수록 추정오차는 작아지기 때문이다.

  • Log-likelihood metric도 있지만 majority voting이 훨씬 낫다.

3. Results

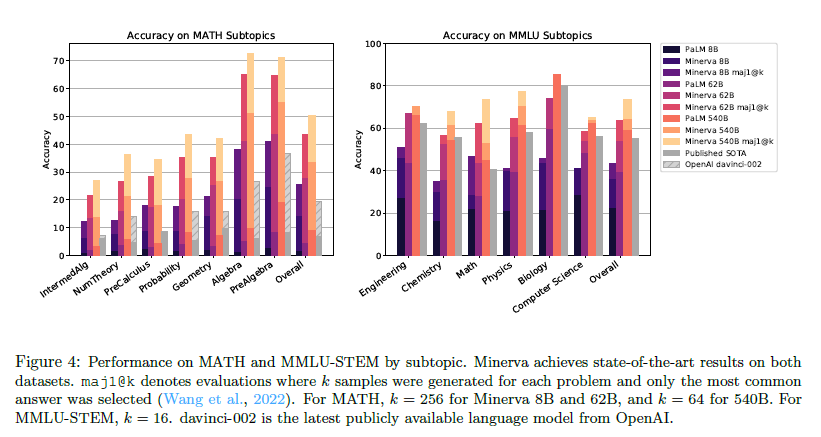
  • Minerva 모델과 다른 모델들을 비교한 표이다.
  • MMLU 평가는 표준 5-shot 프롬프트를 각 topic마다 사용하고 가장 높은 점수의 답을 골랐다. majority voting과 함께 k=16 개의 답을 chain-of-thought prompt를 이용해 sampling하였다.
  • OpenAI의 davinci-002 모델을 공식 추천 temperature(T=0.2) set으로 평가하였다.
    • GSM8k를 제외한 모든 task에서 기존 SOTA보다 성능 향상이 이루어졌다고 볼 수 있다.
  • 본 논문에선 few-shot evaluation이 main focus지만 fine-tuning 역시 진행하였다.
    • Minerva를 MATH 데이터셋에 fine-tuning한 결과는 별 의미 없었지만 PaLM은 상당한 성능 개선이 있었다.
    • 저자들은 비지도 학습 데이터셋의 품질과 다양성이 개선됨에 따라 표준적인 fine-tuning의 한계 효용이 감소했다고 표현하였다.

4. Performance Analysis

4.1 Model Mistakes

  • 모델의 실수를 더 잘 이해하기 위해 Minerva 8B와 62B 모델에서 각각 높은 신뢰도의 majority decision을 기반으로 216개의 문제들을 비교하였다. (최소 15% voting)
    • 8B가 맞고 62B가 틀린 경우 : 15 samples
      • 대부분 추론이나 계산이 잘못된 경우였다.
      • 답이 너무 짧은 경우는 거의 없었다(이땐 중간과정 없이 바로 오답을 내뱉었다).
      • 몇몇의 경우 모델이 실제가 아닌 방정식이나 수학적 사실에 환각(?)을 일으켰다.
    • 62B가 맞고 8B가 틀린 경우 : 201 samples (당연히 이 경우가 더 많다.)
      • 대부분이 다시 추론이나 계산이 잘못된 경우였다.
      • 저자들은 62B 모델이 8B 모델의 스킬 대부분을 가지고 있고 추론과 계산이 robustness에 있어 향상되었다고 말한다.

4.2 False Positives

  • 양적 추론 문제를 해결하는 관점에서 최종 정답이 정답인지는 자동으로 확인이 가능하지만, 안타깝게도 모델의 chain-of-thought 추론을 자동으로 검증하는 방법은 없다고 한다.

    =⇒ 이는 False Positive error의 가능성을 시사한다. (답은 맞았는데 추론과정이 틀린 경우.)

- MATH dataset에서 100개 질문 + 62B model zero temp sampling
- Fasle Positive rate를 측정한 결과 전반적인 비율이 낮고 difficulty level에 오름에 따라 올라간다는 것을 발견했다.
  • pass@k 평가에서 정답이지만 majority voting 결과가 아닌 경우에 주목하였다. (그 중에서도 정답이 한 번만 나타나는 경우)
    • 가장 추론하기 어려운 정답들은 False positive에 있을 가능성이 높기 때문이다.
    • 이 경우, 62B 모델의 pass@256 정확도는 84.5%인데에 비해 False Positive rate이 30%인 것으로 추정하였다.
    • Fals Positives들을 제거할 경우, 정확도가 68%보다 커질 것으로 추측했다.

5. Memorization

  • Minerva의 solution을 해석하는데 있어 중심적인 질문은 성능이 진짜 분석 능력을 반영하는지 아니면 대신에 암기를 하는가이다.
    • 이는 언어 모델이 종종 훈련 데이터의 일부를 암기한다는 많은 선행 연구가 있기에 특히 관련이 있다고 한다. (Trinh and Le, 2018; Radford et al., 2019; Carlini et al., 2022)
    • 저자들은 제곱근이나 삼각함수와 같은 intermediate fact들을 암기하는 것이 모델 솔루션에 있어 중요하다는 사실을 발견했다고 한다.
    • 강력한 성능 = intermediate fact의 recall + truely solution
  • 따라서, 모델이 동일한 질문의 대체 답변을 암기하는 weaker form에 대해서도 조사하였다. 모델이 훈련 데이터에서 외운 정보를 불러와 문제를 해결하는지 평가하기 위해,
    • 1) 훈련 말뭉치에서 문제와 답변을 직접 검색한다.
    • 2) 수정된 문제로 변화를 주고 모델의 견고성을 평가한다.
    • 3) 실제 solution과 모델에 의해 생성된 solution 사이의 중복 정도를 측정하고 이 유사성이 모델 성능에 미치는 영향을 측정한다.
  • 저자들은 모델의 성능이 memorization에 기인할 수 있다는 증거를 찾지 못했다고 한다.

5.1 Training and Evaluation Dataset Overlap

  • Minerva 62B 모델이 정답을 산출한 문제 중 majority voting 점수가 높은 100개의 문제를 선택하였고, 이들이 암기되었을 가능성이 높다고 예상하였다.
  • MATH Web Pages dataset의 500자로 구성된 청크에서 BLUE 점수를 계산하고, 높은 순서대로 250개의 document를 수동으로 검사하였다.
  • 많은 경우 숙제를 도와주는 사이트에서 겹쳤지만 MATH 데이터셋과 겹치는 경우는 하나도 없었다.

5.2 Performance on Modified MATH Problems

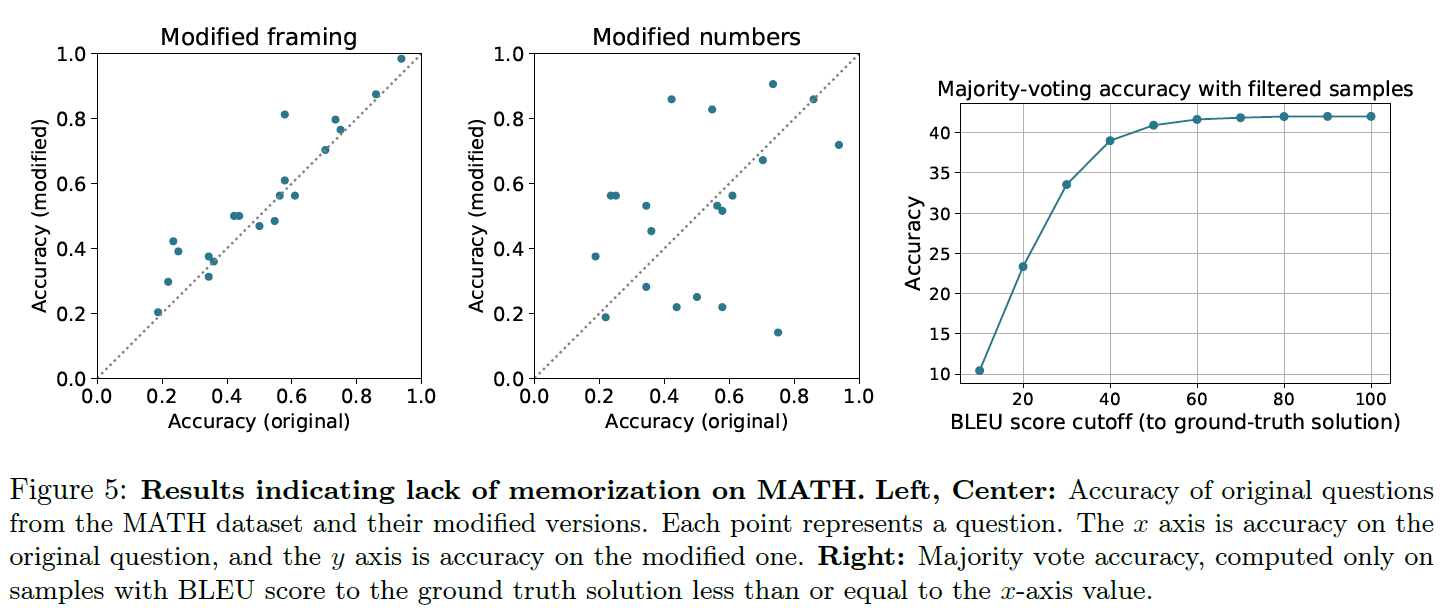
  • Minerva 62B 모델의 majority voting 정답 중 20개를 랜덤하게 가져와 단어(구조)를 약간 수정하거나 숫자를 바꾸고 solution도 적절하게 수정하였다.
  • 수정 전과 후의 정확도를 비교해봤으나 둘 사이에 상관관계가 존재하였고 원래 공식에 대한 clear bias가 존재하지 않았다. ⇒ memorization은 최소한으로 이루어졌음을 보였다.

5.3 BLUE Score Between Ground Truth and Generated Solutions

  • 정답과 모델 답변 사이의 BLUE score 를 측정하여 memorization을 탐지하고자 했다.
  • 62B 모델을 사용하여 MATH dataset의 문제 당 256개의 sample을 분석하는데 모든 정답 표본에 대해 중복 통계를 계산하였다.

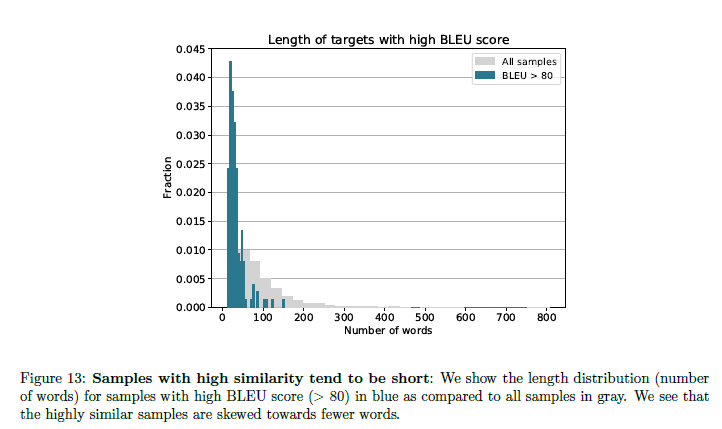
  • 그 결과 5,000개의 test questions 중 160개의 BLUE score가 80 이상임을 발견하였다.
    • 저자들은 이들의 solution이 짧은 경향을 가짐에 주목하였다.
  • 특정 BLUE 점수 임계값 이상의 샘플들을 제거하고 majority voting 정확도를 재계산한 결과(5.2 figure 3) 상대적으로 낮은 유사성(40)까지 강하다는 것을 발견하였다.
    • ground truth와 가장 유사한 경우를 제외하고도 성능이 robust함을 의미한다.
    • 이는 모델 성능이 실제 정답과 매우 가까운 모델 output에서 기인하지 않음을 알 수 있다.

6. Conclusions and Discussion

  • 고품질의 수학 데이터 세트에서 거대 언어 모델을 훈련함으로써 논리적 추론, 수치 계산 및 기호 조작이 필요한 task에서 강력한 성능을 달성할 수 있음을 보였다.
  • Minerva는 외부 도구에 의존하지 않고 autoregressive sampling에만 의존한다.
  • 다만 코드 생성 모델과 형식적 방법들과 같은 다른 모든 접근 방식들의 유용한 요소들이 결합되어 양적 추론문제를 해결해나가야 한다.

6.1 Limitations of Our Approach

  • 모델 답변의 정확도를 자동으로 검증할 방법이 없다.
  • 외부 도구에 엑세스할 수 없어 복잡한 수치 계산이 필요한 작업 수행엔 한계가 있다.
  • 많은 양의 데이터로 훈련되었기에 모델의 특정 기능에 대한 직접적인 제어가 거의 없다.

6.2 Societal Impact

  • 상당한 사회적 영향을 미칠 수 있는 잠재력을 가지고 있지만 아직 멀었다.
  • 모델 성능은 여전히 인간보다 훨씬 낮으며, output의 정확성을 자동 검증할 방법이 없다.
  • 이런 문제가 해결된다면 이 모델의 영향은 대체로 긍정적일 것으로 기대한다.
  • 직접적인 응용법으로는, 누구나 접근 가능하고 저렴한 수학 과외로서 교육 불평등을 개선하는데 도움을 줄 수 있을 것이다.
profile
jihwanyoon
hi!
다음 포스트

[논문리뷰] Chain-of-Thought Prompting Elicits Reasoning in Large Language Models

0개의 댓글