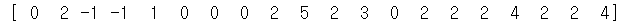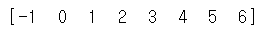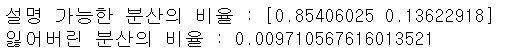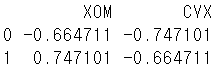수업 47일차

✔ GMM(가우시안 혼합 모델)

• 타원형 데이터에는 잘 동작한다.
• 반달 모양의 데이터나 동심원 형태의 데이터에 취약합니다.

✔ DBSCAN

개요

• 국부적인 밀집도를 추정하는 매우 다른 방식을 사용합니다.
• 임의의 모양을 가진 클러스터를 식별할 수 있습니다.
• 간단하고 직관적인 알고리즘

ex

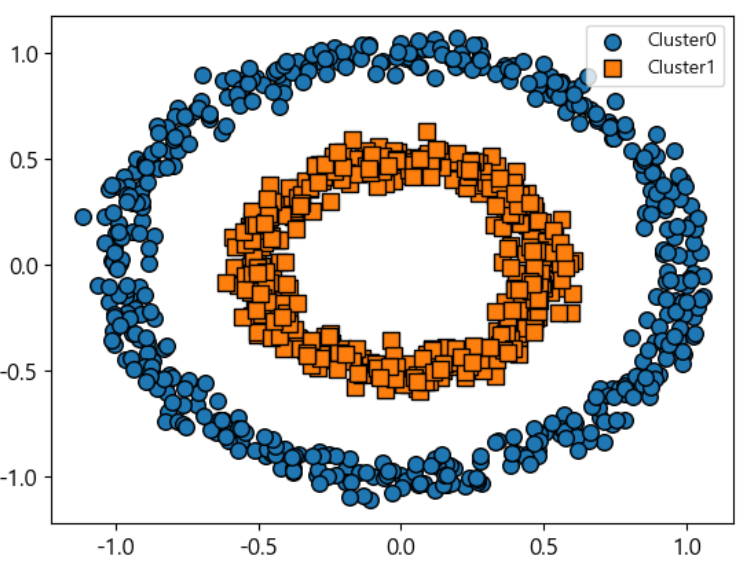
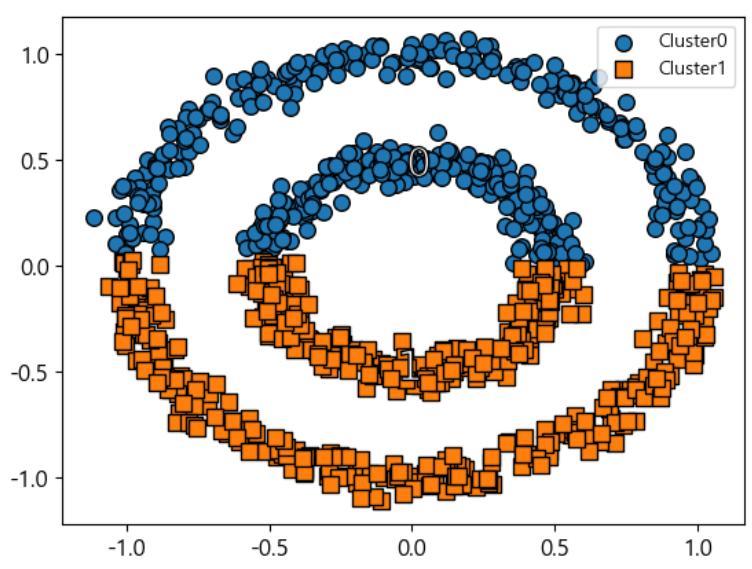
• 내부의 원 모양과 외부의 원 모양을 가진 형태의 데이터 분포의 경우 KNN, K-Means, GMM또는 계층적 클러스터링으로는 효과적인 군집화가 어렵지만 DBSCAN은 가능함
• DBSCAN은 특정 공간 내에 데이터 밀도 차이에 기반한 알고리즘 입니다.

알고리즘

• epsilon
  - 주변 영역
• min points
  - 엡실론 영역에 포함되는 다른 데이터의 개수
• Core Point(핵심 포인트)
  - 주변 영역 내에 최소 데이터 개수 이상의 다른 데이터를 포함한 포인트
• Neighbor Point(이웃 포인트)
  - 주변 영역 내에 존재하는 다른 데이터
• Border Point(경계 포인트)
  - 주변 영역 내에 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지 않지만, 핵심 포인트를 이웃으로 가지고 있는 데이터
• Noise Point(잡음 포인트)
  - 최소 데이터 개수 만큼의 이웃 포인트도 가지지 않고 햄심 포인트도 이웃 포인트로 가지지 않은 데이터
  - 이상치 탐지의 원리

작동 방식

• 알고리즘이 각 샘플에서 epsilon 내에 샘플이 몇 개 놓였는지 세고, 이 지역을 샘플의이웃이라고 부릅니다.
• 이웃 내에 min_samples 개 이상의 데이터가 존재한다면, 핵심 포인트로 간주합니다.
• 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속하고, 이웃에는 다른 핵심 포인트가 포함될 수 있어서 핵심 포인트의 이웃의 이웃은 계속해서 하나의 클러스터를 형성
• 핵심 포인트도 아니고 이웃 포인트도 아닌 잡음 포인트는 이상치 처리

클래스

• sklearn DBSCAN 클래스 이용합니다.
• 초기화 파라미터
  - eps : 엡실론
  - min_samples : 최소 이웃의 개수
  

• 반달 모양 데이터 군집 생성

from sklearn.datasets import make_moons
X,y=make_moons(n_samples=1000,noise=0.05, random_state=42)
plt.scatter(x=X[:,0], y=X[:,1])

• eps 0.05 min_samples를 5로 설정해서 수행

# eps 0.05 min_samples를 5로 설정해서 수행
from sklearn.cluster import DBSCAN
# 모델 생성 및 훈련
dbscan=DBSCAN(eps=0.05,min_samples=5)
dbscan.fit(X)
# 군집된 결과 확인 (-1)은 노이즈
print(dbscan.labels_[:20])

• 핵심 포인트 확인하기

# 핵심 포인트의 개수 확인해보자.
print(len(dbscan.core_sample_indices_))
# 핵심 포인트의 인덱스
print(dbscan.core_sample_indices_)
# 핵심 포인트의 좌표
print(dbscan.components_)

• 실제 클러스터 확인하기

# 클러스터의 종류 확인하기
print(np.unique(dbscan.labels_))

• 이상치를 제외하고 0~6까지 총 7개의 군집으로 나누어졌다.
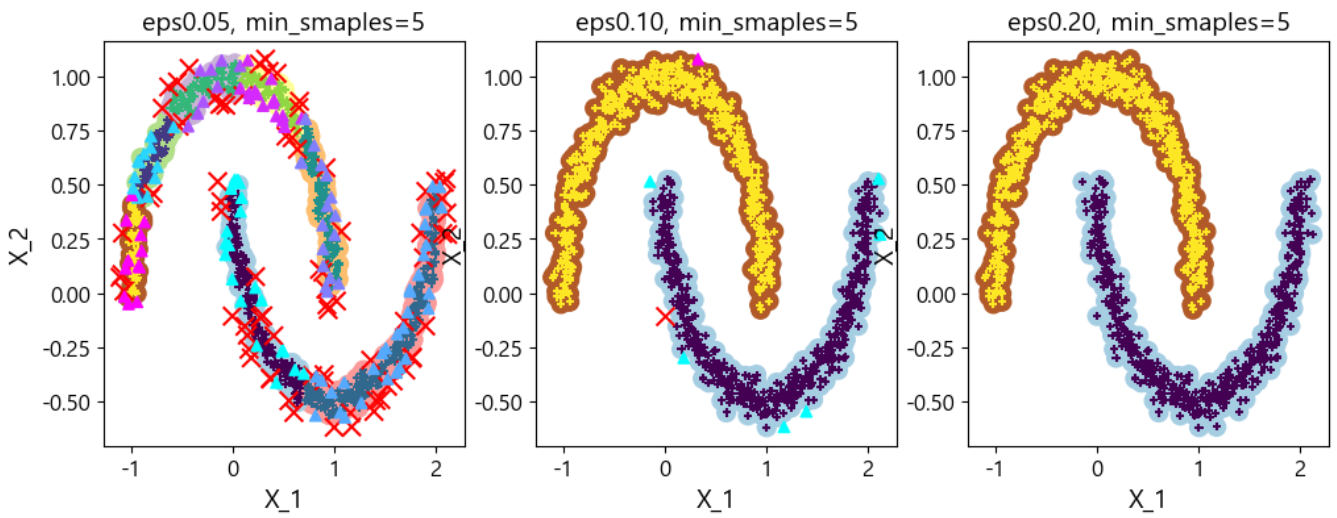
• eps 값을 조금씩 바꾸면서 결과를 다시 확인해보자.
• eps 값이 0.5가 된다면 label은 0, 1로 완벽하게 군집화가 됩니다.
• eps 값 변화하면서 확인하기

def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
    # 데이터 개수만큼 배열 만들고 핵심 포인트만 True 설정
    core_mask=np.zeros_like(dbscan.labels_,dtype=bool)
    core_mask[dbscan.core_sample_indices_]=True
    # 이상치는 반대로 설정
    anomalies_mask=dbscan.labels_==-1
    # 이웃 포인트(핵심, 이상도 아닌 포인트)
    non_core_mask=~(core_mask | anomalies_mask)
    cores=dbscan.components_
    anomalies=X[anomalies_mask]
    non_cores=X[non_core_mask]
#     plt.scatter(cores[:0],cores[:,1], c=dbscan.labels_[core_mask],
#                 makrer='o', s=size, cmap='Paired')
#     plt.scatter(cores[:0],cores[:,1], c=dbscan.labels_[core_mask],
#                 makrer='*', s=20)
    plt.scatter(cores[:, 0], cores[:, 1], c=dbscan.labels_[core_mask], marker='o', s=size, cmap='Paired')
    plt.scatter(cores[:, 0], cores[:, 1], c=dbscan.labels_[core_mask], marker='+', s=20)
#     plt.scatter(anomalies[:0],anomalies[:,1], c=dbscan.labels_[anomalies_mask],
#                 makrer='x', s=100, cmap='r')
#     plt.scatter(non_cores[:0],non_cores[:,1], c=dbscan.labels_[non_core_mask],
#                 makrer='^',cmap='g')
    plt.scatter(anomalies[:, 0], anomalies[:, 1], c=dbscan.labels_[anomalies_mask], marker='x', s=100, cmap='prism')
    plt.scatter(non_cores[:, 0], non_cores[:, 1], c=dbscan.labels_[non_core_mask], marker='^', cmap='cool')
    if show_xlabels:
        plt.xlabel("X_1",fontsize=14)
    else:
        plt.tick.params(labelbottom=False)
    if show_ylabels:
        plt.ylabel("X_2", fontsize=14)
    else:
        plt.tick.params(labelleft=False)
    plt.title("eps{:.2f}, min_smaples={}".format(dbscan.eps,dbscan.min_samples),fontsize=14)

### 엡실론 조정
dbscan1=DBSCAN(eps=0.05, min_samples=5)
dbscan2=DBSCAN(eps=0.1, min_samples=5)
dbscan3=DBSCAN(eps=0.2, min_samples=5)
dbscan1.fit(X)
dbscan2.fit(X)
dbscan3.fit(X)
plt.figure(figsize=(12,4))
plt.subplot(131)
plot_dbscan(dbscan1,X,size=100)
plt.subplot(132)
plot_dbscan(dbscan2,X,size=100)
plt.subplot(133)
plot_dbscan(dbscan3,X,size=100)
plt.show()

예측

• DBSCAN은 predict 같은 예측 함수를 제공하지 않습니다.
• 군집한 뒤의 예측은 분류나 회귀 알고리즘이 더 잘하기 때문입니다.
• 군집 한 결과를 가지고 분류나 회귀 알고리즘을 수행한 뒤,

# 새로운 데이터에 대한 예측
from sklearn.neighbors import KNeighborsClassifier
# 군집한 결과를 가지고 분류 모델이 훈련
knn=KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan3.components_,dbscan3.labels_[dbscan3.core_sample_indices_])

# 예측은 학습한 KNN으로
X_new=np.array([[-0.5, 0], [0,0.5]])
y_hat=knn.predict(X_new)
print(y_hat)
y_hat_proba=knn.predict_proba(X_new)
print(y_hat_proba)

정리

• 매우 간단하지만 강력한 알고리즘
• 클러스터의 모양과 개수에 상관없이 감지할 수 있는 능력이 있음
• 이상치에 안정적이고 하이퍼 파라미터가 2개(eps, min_samples)
• 클러스터 간의 밀집도가 다르면, 모든 클러스터를 잡아내는 것이 거의 불가능
• 계산 복잡도는 O(mlogm) : m 데이터 개수
• sklearn에서는 데이터의 개수에 대해서는 선형으로 증가하지만, eps에 대해서는 o(m^2)만큼 메모리가 필요합니다.

✔ K-Means & GMM & DBSCAN

• K-Means는 Centroid 와의 거리를 이용
  - 클러스터 간의 간격이 조금 멀 때 사용
• GMM은 모든 데이터의 분포를 정규 분포라고 가정
  - 타원형 데이터에 적합
• DBSCAN은 밀집도 기반
  - 데이터가 정규분포 형태가 아닐때
  - 데이터의 분포가 연속적일 때
  - 이상치 탐지를 합니다.

• 시각화 함수 - DB 클러스터링 결과 & DF

# K-Means때문에 istcenter를 넣었습니다.
def visualize_cluster_plot(clusterobj,dataframe, 
label_name, iscenter=True):
    # 클러스터의 중앙점 찾기
    if iscenter:
        centers=clusterobj.cluster_conters_
    unique_labels=np.unique(dataframe[label_name].values)
    markers=['o','s','^','x','*']
    # 이상치 여부
    isNoise=False
    # 클러스터 순회
    for label in unique_labels:
        label_cluster=dataframe[dataframe[label_name]==label]
        # 이 경우는 DBSCAN만
        if label==-1:
            cluster_legend='Noise'
            isNoise=True
        else:
            cluster_legend='Cluster'+str(label)
        plt.scatter(x=label_cluster['ftr1'],y=label_cluster['ftr2'],
                   s=70, edgecolor='k', marker=markers[label],
                   label=cluster_legend)
        if iscenter:
            center_x_y=centers[label]
            plt.scatter(x=center_x_y[0],y=center_x_y[1],s=250,
            color='white',edgecolor='k',marker='$%d$'%label)
    if isNoise:
        legend_loc='upper center'
    else:
        legend_loc='upper right'
    plt.legend(loc=legend_loc)
    plt.show()

• 샘플데이터

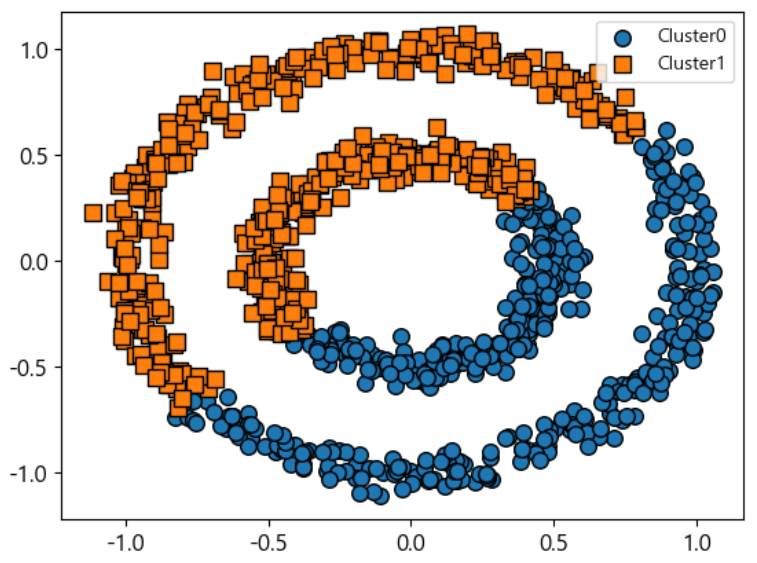
from sklearn.datasets import make_circles
X,y=make_circles(n_samples=1000, shuffle=True, 
                 noise=0.05, random_state=42,
                factor=0.5)
clusterDF=pd.DataFrame(data=X, columns=['ftr1','ftr2'])
clusterDF['target']=y
print(np.unique(clusterDF['target']))
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)

• K-Means는 어떻게 처리 할까?

from sklearn.cluster import KMeans
kmeans=KMeans(n_clusters=2, max_iter=1000, random_state=42)
kmeans_labels=kmeans.fit_predict(X)
clusterDF['kmeans_cluster']=kmeans_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_cluster',
iscenter=True)

• centroid 계산으로 반으로 나누어졌다.
• GMM은 어떻게 처리할까?

from sklearn.mixture import GaussianMixture
gmm=GaussianMixture(n_components=2, random_state=42)
gmm_label=gmm.fit(X).predict(X)
clusterDF['gmm_cluster']= gmm_label
visualize_cluster_plot(gmm, clusterDF, 'gmm_cluster', iscenter=False)

• 타원형으로 처리하더니, 결국 대각선 방향으로 반을 갈라버렸다.
• 이제 DBSCAN을 봐보자.

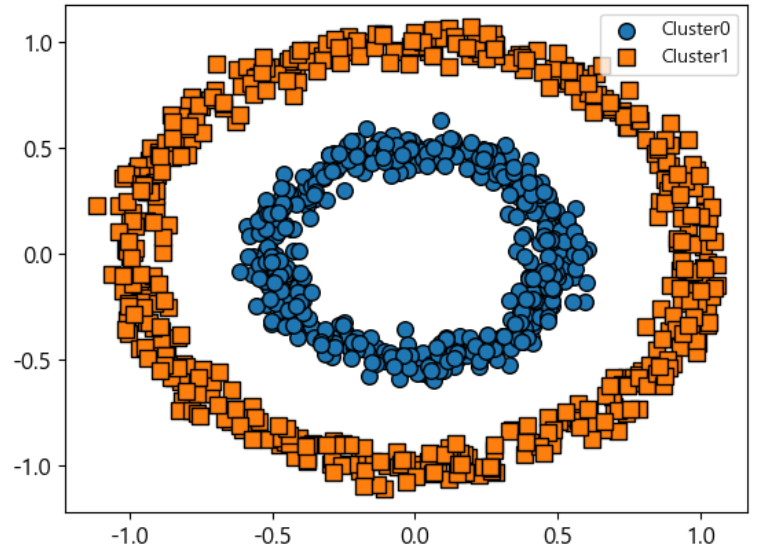
from sklearn.cluster import DBSCAN
dbscan=DBSCAN(eps=0.2, min_samples=7)
dbscan_labels=dbscan.fit_predict(X)
clusterDF['dbscan_cluster']= dbscan_labels
visualize_cluster_plot(dbscan, clusterDF, 'dbscan_cluster',
iscenter=False)

• 이쁘게 분류했다.

✔ BIRCH

• Balanced Iterative Reducing and Clustering
• 대규모 데이터 세트를 위해서 개발
• 특성 개수가 많지 않은 경우(20개 이하), K-Means보다 빠르고 비슷한 결과를 생성합니다.
• 훈련 과정에서 새로운 샘플을 클러스터에 빠르게 할당할 수 있는 정보를 담은 트리구조를 이용합니다.
• 제한된 메모리를 사용해서 대용량 데이터 세트를 다룰 수 있음

장점

• 한 번의 스캔으로 클러스터링

단점

• 숫자 데이터만 다룰 수 있고, 순서에 민감합니다.

from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data
from sklearn.cluster import Birch
brc=Birch(n_clusters=3)
brc.fit(X)

print(iris.target)
y_hat=brc.predict(X)
print(y_hat)

✔ 유사도 전파

• 투표 방식을 이용
• 각 데이터는 자신을 대표할 수 있는데 비슷한 샘플에 투표
• 알고리즘을 수행하다가 수렴된다면, 각 대표와 투표한 샘플이 클러스터를 형성
• 크기가 다른 열러 개의 클러스터를 감지할 수 있지만, 알고리즘의 계산 복잡도가 O(m&2)이라서 대규모 데이터 세트에는 적합하지 않음

✔ 스펙트럼 군집

• 샘플의 유사도 행렬을 받아서 저차원 임베딩을 생성
  - 차원 축소
• 축소된 저차원 공간에서 다른 군집 알고리즘을 수행(sklearn의 경우는 k-Means)
• 복잡한 클러스터 구조를 잘 감지합니다.
• 샘플의 개수가 많거나 클러스터의 크기가 너무 다르면 잘 동작하지 않음

✔ 이상치 탐지와 특이치 탐지를 위한 알고리즘

군집 알고리즘

• 군집을 했을 때, 잘 어울리지 못하는 데이터

PCA(주성분 분석)

• 샘플의 재구성 오차와 이상치의 재구성 오차를 비교하면, 후자가 훨씬 큼

Fast-MCD(Minimum Covariance Determinant)

• 데이터 세트를 정제할 때, 일반적인 데이터는 하나의 가우시안 분포에서 생성되었다고 가정하며, 이 가우시안 분포에서 생성되지 않은 데이터를 이상치로 간주
• 타원형을 잘 감지한다

아이솔레이션 포레스트

• 고차원 데이터 세트에서 이상치 감지를 위한 효과적인 알고리즘
• 무작위로 성장한 결정 트리로 구성된 랜덤 포레스트를 생성하고, 각 노드에서 특성을 랜덤하게 선택하고, 임계값을 설정하고 데이터 세트를 나누는 방식

LOG(Local Outlier Factor)

• 일반적인 데이터의 주위의 밀도와 이웃 주위의 밀도를 비교해서 격리된 정도를 확인

one-class SVM

• 하나의 평면을 이용해서 이 평면에 놓아지지 않는 데이터를 이상치로 간주
• 대규모 데이터 세트에 사용하면 시간이 오래 걸림

✔ 비지도 학습에서의 전처리

• 비지도 학습에서는 데이터를 적절하게 스케일링을 해야 합니다.

• 데이터 크기가 조정되지 않으면, PCA, K-Means 등은 큰 값을 갖는 변수들에 의해 결과가 좌우되고, 작은 값을 갖는 변수들은 무시되는 경우가 발생합니다.

• 범주형 데이터를 사용하게 된다면 KNN과 K-Means에서는 문제가 발생할 수 있습니다.
  - 순서가 없는 데이터들은 원 핫 인코딩을 하게 되는데, 이렇게 되면 다른 feature와 크기가 다를 수 있고, 2가지 값만 가질 수 있기 때문에 영향을 많이 미치게 될 수 있습니다.
  

✔ 차원 축소 (Demesionality Reduction)

개요

• Machine Learning 문제들은 많은 특성을 소유하고 있는 경우가 많습니다.
• 특성이 많다면 훈련을 느리게 할 뿐 아니라, 좋은 솔루션을 찾기가 어려워 집니다.
  - 이를 차원의 저주라고 합니다.

종류

• feature selection
  - 특정 피처에 종속성이 강한 불필요한 featrue 는 제거하고, 데이터의 특성을 잘 나타내는 주요 feature만 선택
• feature extraction
  - 기존들의 feature들을 저차원의 중요 feature로 압축해서 추출
  - 기존 feature가 압축된 것이기 때문에 기존 feature와는 다른 값
  - 더 함축적인 요약 특성으로 추출

주의

• 차원 축소를 수행하면, 일부 정보가 유실되기에, 훈련 속도는 빨라지지만, 시스템의 성능이 조금 나빠질 수 있으며, 파이프라인이 복잡해짐
• 이미지나 텍스트에서 차원 축소를 통해, 잠재적인 의미를 찾을 수 있습니다.
  - 매우 많은 픽셀로 이루어진 이미지 데이터에서 모든 차원을 전부 활용해서 이미지 분류를 하게 된다면, 과대 적합될 가능성이 있기 때문에 차원을 축소하는 것이 예측 성능에 훨씬 도움이 될 수 있습니다.
  

차원의 저주

• 고차원 공간에서는 많은 것이 상당히 다르게 작동
• 단위 면적(1*1 사각형) 안에 존재하는 점을 무작위로 선택한 경우, 경계선에서 0.001 내에 위치할 가능성은 0.4% 정도 되지만, 차원이 높아지면 이 가능성은 매우 높아진다.
• 차원이 높아지면 데이터 사이의 거리도 멀어지게 됩니다.
  - 차원이 높아지면 데이터 사이의 거리가 멀어진다는 것은, 예측해야 하는 새로운 데이터와 모델을 생성할 때, 사용한 훈련 데이터와의 거리도 멀어질 가능성이 높다라는 것을 의미
  - 거리가 멀어지면 외삽(Extrapolation - 보외법)을 훨씬 더 많이 수행해야 해서 불확실성이 높아집니다.
  - 보간은 두 개의 값 사이를 추정하기는 하는데, 최소값과 최대값 사이의 중간 값들을 유추
  - 외삽은 다른 값들 사이의 관계에 기초에서 예측
• 차원이 높아지면 아주 많은 샘플이 필요합니다

투영

• 차원이 많은 경우, 거의 대부분은 특성은 변화가 없고, 다른 특성들이 서로 강하게 연관되어 있다라는 가정
• 스위스 롤 같은 문제가 발생

Manifold 학습

• 고차원 공간에서 휘어지거나 뒤틀린 모양

PCA(Principa Component Analysis) - 주성분 분석

• 여러 변수 간에 존재하는 상관 관계를 이용해서 이를 대표하는 주성분을 추출해 차원을 축소하는 방법
• 일반적으로 변수들은 공변(covary - 같이 변하는 성질)하므로 이러한 공변이 어떻게 일어나는지 알아내는 기법

분산 보존

• 여러 개의 축을 더 적은 개수의 축으로 변환을 할 때 분산의 값이 큰 방향으로 투영을 합니다.
• 분산의 값이 큰 방향으로 투영해야 정보가 가장 적게 손실되기 때문입니다.
• 분산 보존의 원리를 적용해서 만든 축을 주성분이라고 합니다.
  - 이 주성분은 원점에 맞추어진 단위 벡터 형태로 표현하기 때문에 방향은 +나 - 방향이 될수 있음
• 선형 대수 입장에서 보면 PCA는 입력 데이터의 공분산 행렬을 고유 값 분해하고 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환한 것이고, 이 고유 벡터(eigen vector)가 PCA의 주성분 벡터
• 이 벡터의 크기를 고유 값(eigen value)이라고 합니다.
• 행렬 분해를 이용해서 표현합니다.

수행 순서

• 입력 데이터 세트의 공분산 행렬을 생성
• 공분산 행렬의 고유 벡터와 고유 값을 계산합니다.
• 고유 값이 큰 순서대로 k(PCA의 차수)개 만큼 고유 벡터 추출
• 고유 값이 큰 순서대로 추출된 고유 벡터를 가지고 새로운 입력 데이터를 추출합니다.

SVD(특이값 분해)

• 고차원의 데이터를 저차원으로 분해하는 기법
• 추천 시스템을 만들 때 많이 활용합니다.
• numpy에서 제공합니다. numpy.linal.svd 함수

np.random.seed(42)
m=60
angles=np.random.rand(m)*3*np.pi/2-0.5
X=np.empty((m,3))
# print(X)
X_centered=X-X.mean(axis=0)
# 특이값 분해 수행
U,s,Vt=np.linalg.svd(X_centered)
# 주성분 
c1=Vt.T[:,0]
c2=Vt.T[:,1]
print(c1)
print(c2)
# 실제 변환된 결과
W2=Vt.T[:,:2]
X2D=X_centered.dot(W2)
print(X2D)

• 이걸 직접 작업할 필요는 없고 sklearn의 PCA 클래스가 SVD를 이용한 주성분 분석을 구현하고 있다.
• n_componentes파라미터에 원하는 주성분의 개수만 설정하면 됩니다.

np.random.seed(42)
m=60
angles=np.random.rand(m)*3*np.pi/2-0.5
X=np.empty((m,3))
# print(X)
X[:,0]=np.cos(angles)+np.sin(angles)/2+0.1*np.random.randn(m)/2
# 0.1, 0.7은 잡음을 섞이 위한 것이라 아무 숫자나 가능
X[:,1]=np.sin(angles)*0.7+0.1*np.random.randn(m)/2
# 잡음 처리 해주기
X[:,2]=X[:,0]*0.1+X[:,1]*0.3+0.1*np.random.randn(m)
X_centered=X-X.mean(axis=0)
# sklearn
from sklearn.decomposition import PCA
# 2개의 주성분을 추출해주는 PCA 인스턴스
pca=PCA(n_components=2)
# 데이터를 2차원으로 줄이기
X2D=pca.fit_transform(X)
print(X2D)

• 훈련을 하고 난 뒤, PCA 인스턴스의 explained_variance_ratio_속성에 설명 가능한 분산의 비율을 저장합니다.
• 이 개수는 주성분의 개수입니다.

# 분산의 비율
print("설명 가능한 분산의 비율 :",pca.explained_variance_ratio_)
# 첫 번째 주성분이 0.854 만큼의 분산을 설명
# 두 번째 분산은 0.136만큼의 분산을 설명
# 두개의 분산이 있으면 0.99만큼의 분산을 설명하는 것
# 데이터 유실
print("잃어버린 분산의 비율 :", (1-pca.explained_variance_ratio_.sum()))

• PCA 인스턴스의 invers_transform 함수를 이용하면 원래의 데이터로 복원이 가능합니다.
  - 완전 복원은 불가능합니다.
  - 분산이 100%가 아니기 때문입니다.

np.random.seed(42)
m=60
angles=np.random.rand(m)*3*np.pi/2-0.5
X=np.empty((m,3))
X[:,0]=np.cos(angles)+np.sin(angles)/2+0.1*np.random.randn(m)/2
# 0.1, 0.7은 잡음을 섞이 위한 것이라 아무 숫자나 가능
X[:,1]=np.sin(angles)*0.7+0.1*np.random.randn(m)/2
# 잡음 처리 해주기
X[:,2]=X[:,0]*0.1+X[:,1]*0.3+0.1*np.random.randn(m)
X_centered=X-X.mean(axis=0)
print(X[:5])
# sklearn
from sklearn.decomposition import PCA
# 2개의 주성분을 추출해주는 PCA 인스턴스
pca=PCA(n_components=2)
# 데이터를 2차원으로 줄이기
X2D=pca.fit_transform(X)
# print(X2D)
# 2차원으로 줄어든 data를 복원하고 싶다.
X3D_inverse=pca.inverse_transform(X2D)
print(X3D_inverse[:5])

• 차이가 존재하긴 하지만, 엄청 큰 차이는 아닌가..?

# 2개가 배열이 같은지 확인
print(np.allclose(X,X3D_inverse))

• return은 boolean

# 오차의 평균
print(np.mean(np.sum(np.square(X3D_inverse - X), axis=1)))
# 각 행의 오차 구하기 -이를 이용해서 이상치 탐지 가능
print(np.sum(abs(X3D_inverse-X), axis=1))
# 주성분 확인
print(pca.components_)

주식 데이터를 이용한 주성분 분석

• 주성분은 분산의 크기를 큰 방향으로 생성
  - 분산 보존 법칙

• Data Load

# gz-> 압축
sp500_px=pd.read_csv('./data/sp500_data.csv.gz',index_col=0)
oil_px=sp500_px[['XOM','CVX']]
oil_px.head()

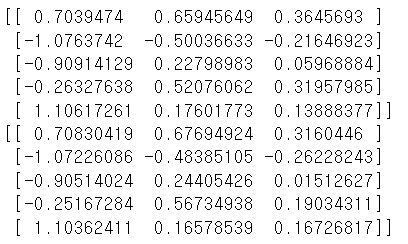
• 주성분 분석의 결과를 DataFrame으로 생성해서 출력

pca=PCA(n_components=2)
pca.fit(oil_px)
loadings=pd.DataFrame(pca.components_,columns=oil_px.columns)
print(loadings)

• 결과 해석
  - 2개의 주성분으로 생성한 경우, 첫 번째 성분은 상관관계를 의미하는 계수이고, 두 번째 성분은 값이 달라지는 지점을 의미합니다.
• 주성분을 시각화

# 주성분 시각화
plt.scatter(oil_px['XOM'],oil_px['CVX'])

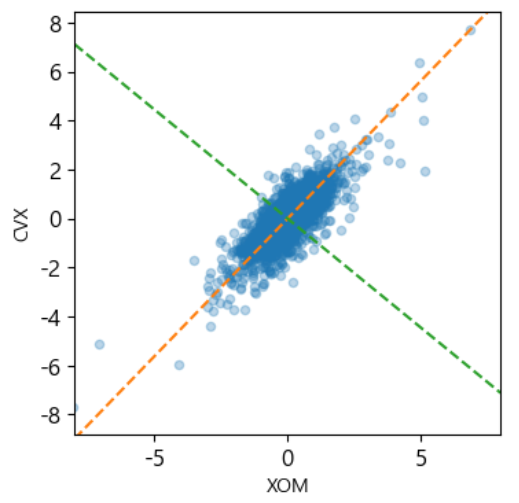
def abline(slope, intercept, ax):
    x_vals=np.array(ax.get_xlim())
    return(x_vals,intercept+slope*x_vals)
ax=oil_px.plot.scatter(x="XOM", y='CVX', alpha=0.3, figsize=(4,4))
ax.set_xlim(-8,8)
ax.set_ylim(-8.8)
ax.plot(*abline(loadings.loc[0,'CVX']/loadings.loc[0,'XOM'],0,ax),
       '--',color='C1')
# C2 녹색
ax.plot(*abline(loadings.loc[1,'CVX']/loadings.loc[1,'XOM'],0,ax),
       '--',color='C2')
plt.show()

• 여러 개의 속성으로 확장하는 것이나 여러 개의 주성분을 추출하는 것도 가능
• 주성분 분석은 수치형 데이터에만 사용 가능합니다
• 범주형, 문자열 그리고 날짜 타입은 분산이 근본적으로 없기에 사용 불가능 합니다.
• 범주형이나 문자열은 개수나 분포의 비율이 의미를 갖는 데이터이지, 평균이나 합계를 구하는 데이터가 아닙니다.

주성분에서의 중요도

• 주성분의 상대적인 중요도를 표시해주는 시각화 방법을 scree plot이라고 합니다.
• 상위 주성분들의 중요도를 파악해서 피처를 제거하고 분류나 회귀를 적용하는 것도 좋은 방법 중의 하나가 됩니다.

• feature의 중요도를 파악해보자.

syms=sorted(['AAPL','MSFT','CSCO','INTC','CVX',
             'XOM','SLB','COP', 'JPM','WFC','USB',
             'AXP','WMT','TGT','HD','COST'])
top_sp=sp500_px.loc[sp500_px.index>='2011-01-01',syms]
top_sp.head()

# feature의 중요도를 파악할 것이라서 주성분의 개수를 설정하지 않음
sp_pca=PCA()
sp_pca.fit(top_sp)

# 설명 가능한 분산의 비율을 확인
print(sp_pca.explained_variance_)

explained_variance=pd.DataFrame(sp_pca.explained_variance_)
ax=explained_variance.head(10).plot.bar(legend=False, figsize=(4,4))
ax.set_label('COMPONANT')
plt.show()

# 5개의 주성분에 미치는 중요도를 DF로 생성

3

적절한 차원 수 선택

• 데이터 시각화를 위해서 차원을 축소할 때는 2개나 3개로 축소합니다.
  - 그래프는 2차원이나 3차원만 표시 가능
• 차원수는 충분한 분산 비율을 설명될 때 까지 더해가면서 설정
• PCA 인스턴스를 만들 때 n_components에 0.0에서 1.0 사이의 숫자를 설정하면, 설명 가능한 분산 비율이 적용되어서 PCA를 수행
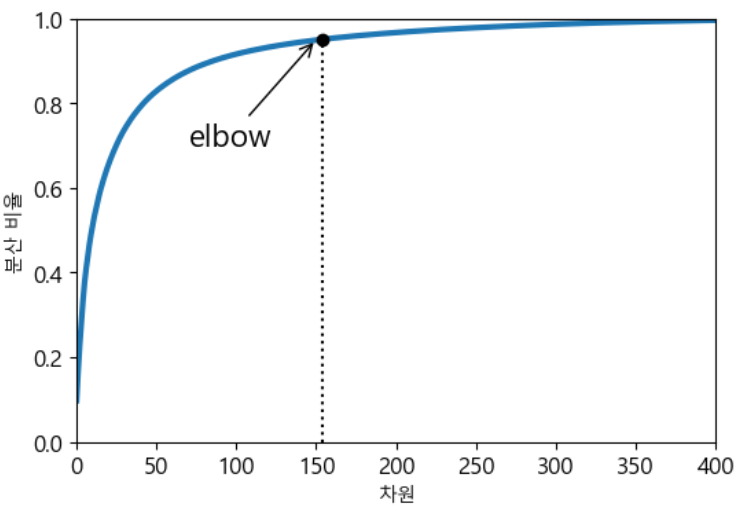
• 차원 수에 대한 분산 설명 비율을 그래프로 그려서 elbow를 찾아서 설정하기도 합니다.

MNIST 이미지 데이터에서 적절한 차원 수 찾기 - 압축해서 예측 작업에 사용

# 데이터 로드
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
mnist=fetch_openml('mnist_784', version=1, as_frame=False)
mnist.target=mnist.target.astype(np.uint8)
X=mnist['data']
y=mnist['target']
X_train,X_test,y_train,y_test=train_test_split(X,y)
print(X_train.shape)

• 출력을 보면 784차원이다.
• 적절한 차원의 개수를 찾기 위해서 차원의 개수를 설정하지 않고 분산의 비율보다 큰 개수를 찾기 (권장 X)

pca=PCA()
pca.fit(X_train)
cumsum=np.cumsum(pca.explained_variance_ratio_)
d=np.argmax(cumsum>=0.95)+1
print(d)

• 154개가 나왔다.
• 방법 2 - 결과를 시각화해서 elbow를 찾는 방식(그다지 권장 X)

plt.figure(figsize=(6,4))
plt.plot(cumsum,linewidth=3)
plt.axis([0,400,0,1])
plt.xlabel('차원')
plt.ylabel('분산 비율')
plt.plot([d,d],[0,0.95],'k:')
plt.plot([d,d],[0.95,0.95],'k:')
plt.plot(d,0.95,'ko')
plt.annotate("elbow", xy=(150,0.95), xytext=(70, 0.7),
            arrowprops=dict(arrowstyle="->"), fontsize=16)
plt.show()

• 방법 3 : 분산비율이 0.95이상인 PCA 만들면 된다.(만들때 집어넣기)(권장)

pca=PCA(n_components=0.95)
X_reduced=pca.fit_transform(X_train)
print(pca.n_components_)
print(np.sum(pca.explained_variance_ratio_))

• 빠르게 잘 나온다.

차원 압축을 해볼거에요

• 차원을 축소하면 데이터의 크기가 줄어듦
  - 분산 크기 95% 유지시 차원 개수가 154개
  - 분산은 유지되고 데이터의 크기는 20% 정도로 압축
• 압축을 하면 SVM같은 알고리즘에서 속도가 향상
• inverse_transform이라는 함수를 이용하면 원래의 차원으로 복원
  - 투영 과정에서 일정량의 정보를 유실했기 때문에, 원본과 동일하지는 않음
• 원본 데이터와 재구성된 데이터(압축 하고 복원된 데이터) 사이의 평균 제곱 거리를 재구성 오차(Reconstruction Error)라고 합니다.

• 복원한 이미지와 원래 이미지

pca=PCA(n_components=154)
X_reduced=pca.fit_transform(X_train)
X_recovered=pca.inverse_transform(X_reduced)
print(X_recovered.shape)

• shape으로 잘 복원되었는지 확인할 수 있다.

def plot_digits(instances, images_per_row=5, **options):
    size=28
    # 한 줄에 출력할 이미지 개수 설정
    image_per_row=min(len(instances),images_per_row)
    # 1차원 이미지를 2차원으로 재구성하기
    images=[instances.reshape(size,size) for instances in instances]
    # 행의 개수 계산
    n_rows=(len(instances)-1)//images_per_row+1
    row_images=[]
    n_empty=n_rows*images_per_row-len(instances)
    images.append(np.zeros((size*size*n_empty)))
    for  row in range(n_rows):
        rimages=images[row*images_per_row : (row+1)*images_per_row]
        row_images.append(np.concatenate(rimages,axis=1))
    image=np.concatenate(row_images, axis=0)
    plt.imshow(image, cmap=mpl.cm.binary, **options)
    plt.axis('off')

plt.figure(figsize=(7,4))
plt.subplot(121)
plot_digits(X_train[::2100])
plt.title("원본 이미지", fontsize=16)
plt.subplot(122)
plot_digits(X_recovered[::2100])
plt.title("압축 이미지", fontsize=16)
plt.show()

• 손실이 크게 난것 같지는 않은데...

랜덤 PCA

• PCA 인스턴스를 만들 때, svd_solver매개변수에 randomized를 설정하면, sklearn은 랜덤 PCA를 수행하는데, 랜덤 PCA는 처음 몇개의 주성분에 대한 근사값을 빠르게 찾는 알고리즘이다.
• 시간 복잡도가 훨씬 줄어듭니다.
• 완전한 SVD를 이용하는 방식은 O(m*n^2) +O(n^3) 이다.
• 랜덤 PCA는 O(m*주성분개수^2)+O(주성분개수^3) 이다.
  - 당연히 주성분 개수가 feature 개수보단 적기 때문에 빨라질 수 밖에 없다.
• sklearn의 PCA의 svd_solver는 기본 값 auto인데, atuo는 주성분 개수나 데이터의 개수나 차원의 개수의 80%보다 작으면 랜덤 PCA를 수행하고, 그렇지 않으면 완전 SVD 방식을 사용
• 완전한 SVD 수행을 할 것이라면 svd_solver에 full을 설정하면 된다.

%%time
pca=PCA(n_components=154, svd_solver='full')
X_reduced=pca.fit_transform(X_train)

%%time
pca=PCA(n_components=154, svd_solver='randomized')
X_reduced=pca.fit_transform(X_train)

• 확실하게 시간 차이가 난다.

%%time
pca=PCA(n_components=154)
X_reduced=pca.fit_transform(X_train)

• 80% 밑이기에 auto 는 randomized가 될 것이다.

점진적 PCA

• PCA의 또 다른 문제점은 SVD 알고리즘을 수행하기 위해서, 전체 데이터를 메모리에 로드하고 수행해야 한다.
• 점진적 PCA(Incremental PCA - IPCA)는 훈련 데이터를 미니 배치(mini batch)로 나눈 뒤, PCA 알고리즘에 한 번에 하나의 배치를 주입하고 훈련을 하는 방식
• 데이터가 아주 클 때, 온라인 학습(데이터가 수시로 대입되는 경우)을 할 때 나눠서 학습하면 매우 좋다.
• numpy의 memmap이라는 클래스를 사용하면, 하드 디스크의 이진 파일에 저장된 배열을 메모리에 들어있는 것 처럼 사용할 수 있는데, 이 클래스는 필요할 때 데이터를 메모리에 적재함.
  - 이것이 IPCA랑 동일한 방식으로 수행
• sklearn에서는 IncrementalPCA 클래스를 이용해서 이 기능을 제공합니다.
  - 데이터를 나누어서 훈련하고 예측을 할 수 있습니다.