수업 46일차

✔ Kaggle

• 데이터 인코딩, 스케일링 등의 전처리와 하이퍼 파라미터 튜닝까지 진행해봤다.
• 더 할 수 있는게 있을까?
  - Kaggle은 train과 test 셋이 분리되어 있으니, train_test_split을 하지 말아보자.

'''
# 훈련에 사용할 데이터와 검증을 위한 데이터 분리
from sklearn.model_selection import train_test_split
# 2:1 target 차이 많이 나이게 층화 추출로
# 테스트 데이터와 검증용 데이터 생성하기
X_train,X_valid,y_train,y_valid=train_test_split(X_train,y,
                                                test_size=0.1,
                                                random_state=42,
                                                stratify=y)
'''
# 여기서 valid를 없애보자.
'''
# 평가지표 - ROC AUC : pred_proba가 필요하다
y_valid_preds=logistic_model.predict_proba(X_valid)[:,1]
from sklearn.metrics import roc_auc_score
roc_auc=roc_auc_score(y_valid, y_valid_preds)
print("평가 점수 : ", roc_auc)
'''
# 이것도 의미가 없을 것이다.

• 학습 코드

from sklearn.model_selection import GridSearchCV
logistic_model=LogisticRegression()
lr_params={
    'C':[0.1,0.125,0.2],
    'max_iter':[800,900,1000,1200],
    'solver':['liblinear'],
    'random_state':[42,20,26]
}
grdisearch_logistic_model=GridSearchCV(estimator=logistic_model,
                                      param_grid=lr_params,
                                      scoring='roc_auc',
                                      cv=5)
grdisearch_logistic_model.fit(X_train,y)
print("최적의 파라미터 : ", grdisearch_logistic_model.best_params_)

• 결과 확인

ㄹ

• 범주형 데이터가 많은 경우에는 Decision Tree를 사용하는 모델보다는 Logistic Regression이나 SVM이 더 좋은 성능을 나타내는 경우가 종종 있다.

Kaggle - 대여 수요 예측하기

• data
  - https://www.kaggle.com/c/bike-sharing-demand/data

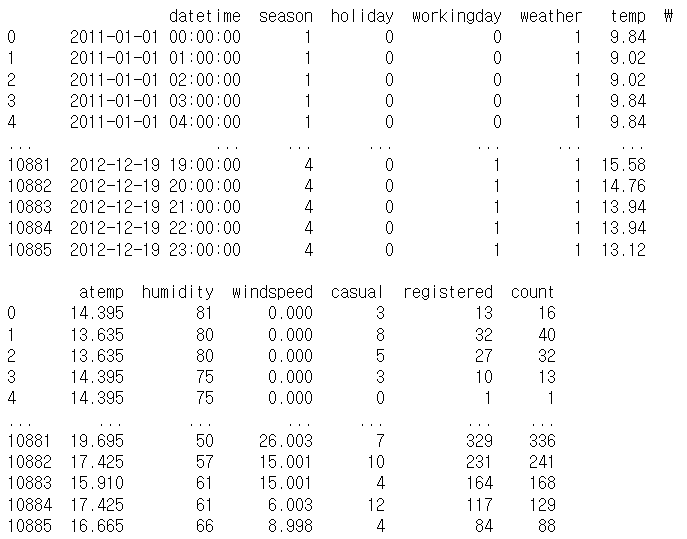
# 다시 데이터를 가져오자.
data_path='./data/bike/'
bike_df=pd.read_csv(data_path+'train.csv')
print(bike_df)
bike_df.info()

---

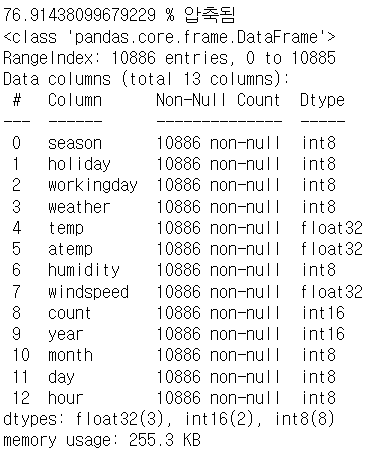
• 결측치는 존재하지 않고, datetime을 제외한 모든 컬럼은 숫자 자료형

feature 정보

• datetime : hourlydate+timestamp
• season : 1-봄, 2-여름, 3-가을, 4-겨울
• hoildy
  - 1: 토,일요일 같은 주말을 제외한 국경일 등의 휴일
  - 0 : 휴일이 아닌 경우
• workingday
  - 1 : 토,일요일이 아닌 주중
  - 2 : 주말 및 휴일
• weather
  - 1 : 맑음
  - 2 : 안개
  - 3 : 눈, 비
  - 4 : 심한 눈, 비
• temp : 온도
• atemp : 체감온도
• humidity : 습도
• windspeed : 풍속
• casual : 사전 등록을 안한 사용자가 대여한 횟수
• registered : 사전 등록한 사용자가 대여한 횟수
• count : 대여한 횟수

---

전처리

• 날짜

# datetime 을 날짜 타입으로
bike_df['datetime']=bike_df['datetime'].apply(pd.to_datetime)
bike_df.info()

bike_df['year']=bike_df['datetime'].apply(lambda x: x.year)
bike_df['month']=bike_df['datetime'].apply(lambda x: x.month)
bike_df['day']=bike_df['datetime'].apply(lambda x: x.day)
bike_df['hour']=bike_df['datetime'].apply(lambda x: x.hour)
bike_df.head()

• 불필요한 컬럼 제거

# 불필요한 컬럼 제거
drop_columns=['datetime','casual','registered']
bike_df.drop(drop_columns,axis=1, inplace=True)

데이터 다운캐스팅

• pandas는 데이터를 읽어올 때, 숫자 타입의 경우에는 int64나 float64로 읽어오는데, 이 자료형은 가장 큰 숫자 자료형이다.
• 데이터가 많은 경우에 메모리 낭비가 심합니다.
• 컬럼마다 max값을 보고 결정하면 될까?
• 숫자의 범위를 확인해보고, 정수의 경우는 int64대신에 int8이나 int16dmf tkdydgksms rjtdmf rhfu
  - integer나 float을 사용하는 것도 고려하자

# downcasting 함수
def downcast(df):
    # 용량이 크면 1024제곱해서 mb 단위로 메모리 확인
    start_mem=df.memory_usage().sum()/(1024) 
    for col in df.columns:
        dtype_name=df[col].dtype.name
        if dtype_name=='object':
            pass
        elif dtype_name=='bool':
            df[col]=df[col].astype('int8')
        elif dtype_name.startswith('int')or
        (df[col].round()==df[col]).all():
            df[col]=pd.to_numeric(df[col],downcast='integer')
        else:
            df[col]=pd.to_numeric(df[col],downcast='float')
    end_mem=df.memory_usage().sum()/(1024)
    print(100*(start_mem-end_mem)/start_mem,"% 압축됨")
    return df

bike_df=downcast(bike_df)
bike_df.info()

---

garbage collection의 호출

• data를 제거하면, 나중에 garbage collection이 호출되어서 메모리 정리를 하게 되는데, 이 시점은 우리가 정확히 알기가 어렵습니다.

평가 지표 함수를 생성 - MSE, RMSE, RMSLE

# 평가지표
from sklearn.metrics import mean_squared_error, mean_absolute_error
import numpy as np
# rmsle
def rmsle(y,pred):
    # log함수는 NaN에서 문제 발생하기에 log1p함수 이용
    log_y=np.log1p(y)
    log_pred=np.log1p(pred)
    squared_error=(log_y-log_pred)**2
    rmsle=np.sqrt(np.mean(squared_error))
    return rmsle
def rmse(y,pred):
    return np.sqrt(mean_squared_error(y,pred))
def evaluate_regr(y,pred):
    rmsle_val=rmsle(y,pred)
    rmse_val=rmse(y,pred)
    mae_val=mean_squared_error(y,pred)
    print('RMSLE:{0},RMSE:{1},MAE:{2}'
    .format(rmsle_val,rmse_val,mae_val))

단순 선형회귀

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
y_target=bike_df['count']
X_features=bike_df.drop(['count'],axis=1)
X_train,X_test,y_train,y_test=train_test_split(X_features, y_target,
                                      test_size=0.3,random_state=42)
lr_reg=LinearRegression()
lr_reg.fit(X_train,y_train)
pred=lr_reg.predict(X_test)
evaluate_regr(y_test,pred)

오차 확인

# 오차가 큰 값 확인
def get_top_error_data(y_test,pred,n_tops=5):
    result_df=pd.DataFrame(y_test.values ,columns=['실제 대여 횟수'])
    result_df['예측한 대여 횟수']=np.round(pred)
    result_df['차이']=np.abs(result_df['실제 대여 횟수']-
    result_df['예측한 대여 횟수'])
    print(result_df.sort_values('차이', ascending=False)[:n_tops])
get_top_error_data(y_test, pred, n_tops=5)

타겟을

## 분포 확인 
y_target.hist()
# 차이가 많이 난다면 로그 변환을 해보자.

# 타겟의 로그 변환
y_log_transform=np.log1p(y_target)
y_log_transform.hist()

y_target_log=np.log1p(y_target)
X_train,X_test,y_train,y_test=train_test_split(X_features,
											y_target_log,
       						test_size=0.3,random_state=42)
lr_reg=LinearRegression()
lr_reg.fit(X_train,y_train)
# target은 로그변환된 상태이다.
# 원래의 값으로 되돌려야 하는 것을 절대 잊지말자
pred=lr_reg.predict(X_test)
y_test_exp=np.expm1(y_test)
pred_exp=np.expm1(pred)
evaluate_regr(y_test_exp,pred_exp)

Feature 인코딩 & 회귀계수 확인

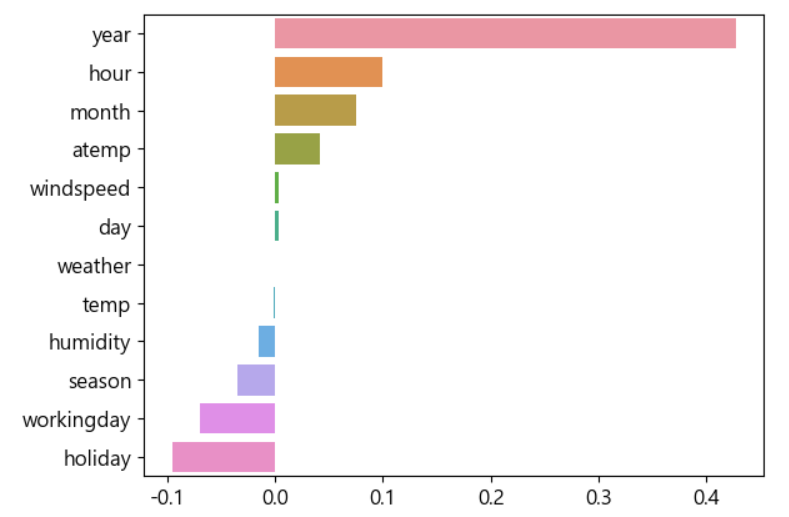
# 회귀계수를 먼저 확인하자
coef=pd.Series(lr_reg.coef_,index=X_features.columns)
coef_sort=coef.sort_values(ascending=False)
import seaborn as sns
sns.barplot(x=coef_sort.values, y=coef_sort.index)

• 단순 int라서 year가 2000년대라서 크게 가져가는 문제가 있는 것 같다.

범주형 데이터의 원 핫 인코딩

# 원핫인코딩
X_feature_ohe=pd.get_dummies(X_features,columns=['year','month',
                                                'day', 'hour',
                                                'holiday',
                                                'workingday',
                                                'season','weather'])
X_feature_ohe.head()

X_train,X_test,y_train,y_test=train_test_split(X_feature_ohe, 
                                               y_target_log,
                                              test_size=0.3,
                                               random_state=42)

• 모델 받아서 훈련하고 예측하는 함수 만들어서 쓰자

# 모델과 데이터를 받아서 훈련하고 평가지표를 출력하는 함수
# 로그까지 생각해
def get_model_predict(model, X_train,X_test,y_train,y_test,
is_expm1=False):
    model.fit(X_train,y_train)
    pred=model.predict(X_test)
    if is_expm1:
        y_test=np.expm1(y_test)
        pred=np.expm1(pred)
    print(model.__class__.__name__)
    evaluate_regr(y_test,pred)

lr_reg=LinearRegression()
get_model_predict(lr_reg, X_train,X_test,y_train,
y_test,is_expm1=True)

• 범주형을 다 ohe해주니 엄청 성능이 늘었다.

이번엔 규제를 넣어보자.

from sklearn.linear_model import Ridge, Lasso
ridge_reg=Ridge(alpha=10)
lasso_reg=Lasso(alpha=0.1)
get_model_predict(ridge_reg,X_train,X_test,
y_train,y_test, is_expm1=True)
get_model_predict(lasso_reg,X_train,X_test,
y_train,y_test, is_expm1=True)

트리 모델도 해볼까?

from sklearn.ensemble import RandomForestRegressor,
GradientBoostingRegressor
from xgboost import XGBRegressor
rf_reg=RandomForestRegressor(n_estimators=500)
gbm_reg=GradientBoostingRegressor(n_estimators=500)
xgb_reg=XGBRegressor(n_estimators=500)
# xgboost는 dataframe을 주면 오류가 생기는 경우가 있습니다.
# 그러면 data들을 X_train.values 로 해서 ndarray로 바꿔주자. 4개다
for model in [rf_reg,gbm_reg, xgb_reg]:
    get_model_predict(model,X_train,X_test,y_train,y_test,
    is_expm1=True)

✔ Clustering - 군집

• 비슷한 샘플들을 구별해서 하나의 클러스터로 묶는 작업
• 비지도 학습 이다.
  - 레이블이 없는 학습
  - 답이 존재하지 않는 학습
• 이용되는 분야
  - 고객 분류
  - 데이터 분석 : 각 클러스터로 나눈 후 따로 분석
  - 차원 축소
  - 이상치 탐지 : 모든 클러스터에 친화적이지 않은 데이터를 이상치로 간주
  - 준 지도학습 : 레이블이 일부부만 존재하면, 군집 수행해서 새 레이블 생성
  - 검색 엔진
  - 이미지 분할
• sklearn 에서는 다양한 유형의 군집화 알고리즘을 테스트 해보기 위한 샘플 데이터를 생성하는 APi를 제공합니다.
  - make_blobs(), make_classification, make_circle, make_moon()...
  - 군집을 얼마나 효율적으로 했는지확인하기 위한 target을 같이 생성

샘플 데이터를 이용한 군집

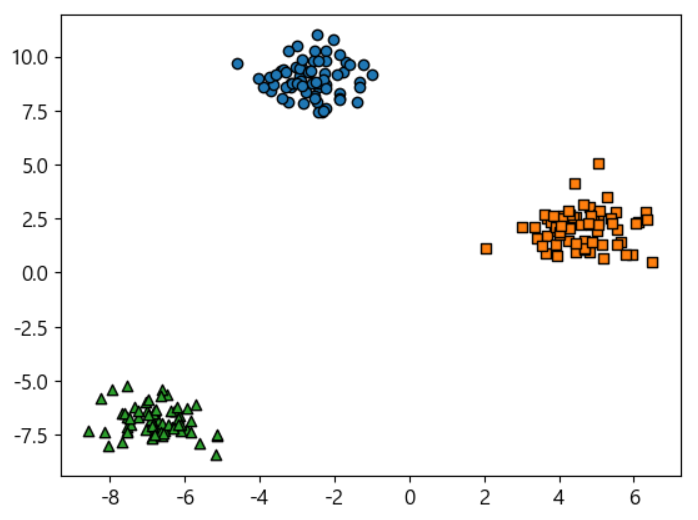
from sklearn.datasets import make_blobs
# 200ro 데이터 생성 피처 2개
# 중심 3개 표준편차 0.8
X,y=make_blobs(n_samples=200,n_features=2,centers=3,cluster_std=0.8,
               random_state=42)
print(X.shape,y.shape)
unique,counts=np.unique(y,return_counts=True)
print(unique)
print(counts)

# 해석을 편하게 하기 위해 DataFrame화 시키자
clusterDF=pd.DataFrame(data=X,columns=['ftr1','ftr2'])
clusterDF['target']=y
clusterDF.head()

# 데이터 분포 확인
target_list=np.unique(y)
markers=['o','s','^','P','D','H','x']
for target in target_list:
    target_cluster=clusterDF[clusterDF['target']==target]
    plt.scatter(x=target_cluster['ftr1'],y=target_cluster['ftr2'], 
               edgecolor='k', marker=markers[target])

from sklearn.mixture import GaussianMixture
y_pred=GaussianMixture(n_components=3,random_state=42)
.fit(X).predict(X)
print(y_pred)
print(y)

# 매핑된 격허ㅣ
from scipy import stats
mapping={}
for class_id in np.unique(y):
    mode, _=stats.mode(y_pred[y==class_id])
    mapping[mode[0]]=class_id
print(mapping)

✔ 과일 이미지 군집

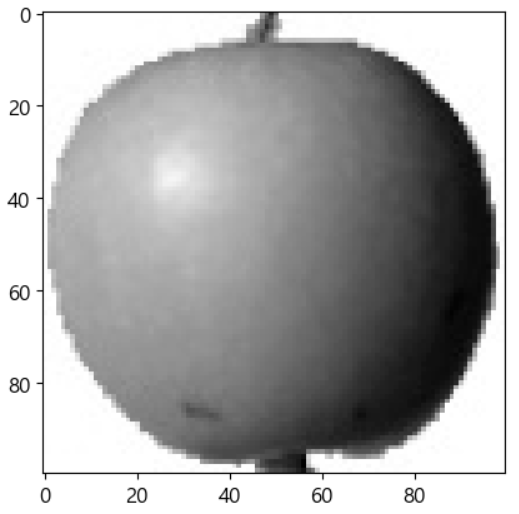
# 데이터 가져오기
fruits=np.load('./data/fruits_300.npy')
# 데이터 300개이고 이미지는 100*100 grayscale
print(fruits.shape)
# 세로 픽셀을 출력하니 0~255 사이 숫자
print(fruits[0,0,:])

# 이미지 출력
# 관심을 갖는 것은 물체이기에 
# 물체 이외는 흰색으로 보여지는게 더 나을 수 있음
plt.imshow(fruits[1], cmap='gray_r')
plt.show()

---

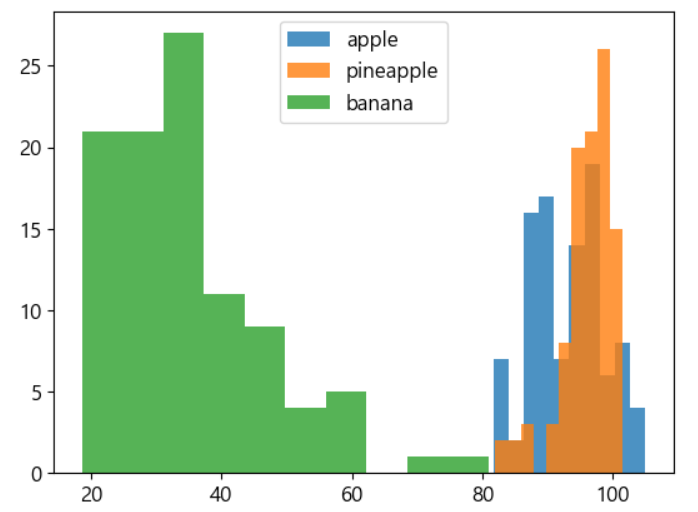
# 이미지 데이터를 비교하기 위해서는 1차원으로 변경해야 합니다.
# 방법 1 - reshape
# 얘는 배열안에 배열로 
print(fruits[0].reshape(-1,100*100))
print(fruits[0].reshape(-1,100*100).shape)
# 방법 2 - flatten
# 얘는 단순 배열로
print(fruits[0].flatten())
print(fruits[0].flatten().shape)

# 이미지를 reshape로 1차원으로 쭉 바꾸자
apple=fruits[0:100].reshape(-1,100*100)
pineapple=fruits[100:200].reshape(-1,100*100)
banana=fruits[200:300].reshape(-1,100*100)
print(apple.shape)

# 이미지들의 평균을 출력해보자.
# 이미지들끼리 비슷비슷하다
print(apple.mean(axis=1))
print(pineapple.mean(axis=1))
print(banana.mean(axis=1))

# 평균을 시각화
plt.hist(np.mean(apple,axis=1),alpha=0.8)
plt.hist(np.mean(pineapple,axis=1),alpha=0.8)
plt.hist(np.mean(banana,axis=1),alpha=0.8)
plt.legend(['apple','pineapple','banana'])
plt.show()

• 바나나는 따로 있어서 구분을 잘 할 것으로 보이지만, 사과와 파인애플을 잘 구별할 수 없을 것이라고 생각한다.

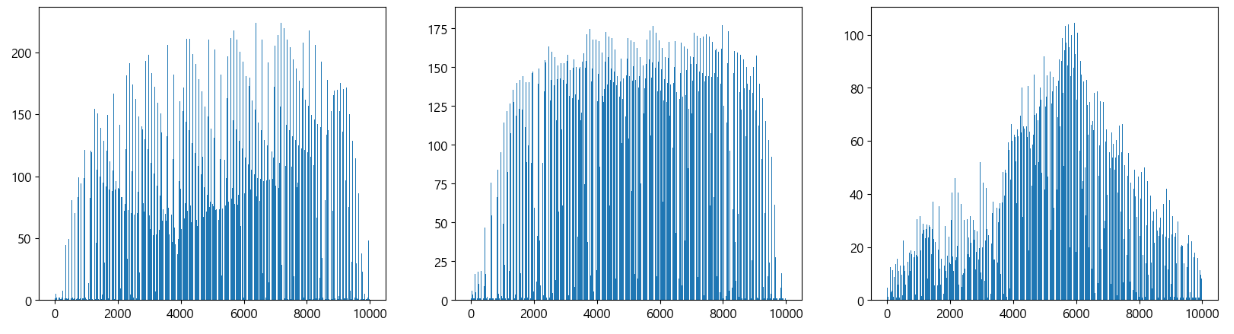
# 픽셀 단위로 평균을 찍어보자.
fig,axs=plt.subplots(1,3,figsize=(20,5))
axs[0].bar(range(10000),np.mean(apple,axis=0))
axs[1].bar(range(10000),np.mean(pineapple,axis=0))
axs[2].bar(range(10000),np.mean(banana,axis=0))
plt.show()

• 사과 파인애플 바나나이다.
• 이제 평균을 가지고 이미지를 만들어 볼 것이다.

 # 평균을 가지고 이미지 생성
apple_mean=np.mean(apple,axis=0).reshape(100,100)
pineapple_mean=np.mean(pineapple,axis=0).reshape(100,100)
banana_mean=np.mean(banana,axis=0).reshape(100,100)
fig,axs=plt.subplots(1,3,figsize=(20,5))
axs[0].imshow(apple_mean, cmap='gray_r')
axs[1].imshow(pineapple_mean, cmap='gray_r')
axs[2].imshow(banana_mean, cmap='gray_r')
plt.show()

• K-means 비스무리하게..

# 모든 데이터에서 사과의 평균을 뺀 절대값 구하기
abs_diff=np.abs(fruits-apple_mean)
abs_mean=np.mean(abs_diff,axis=(1,2))
print(abs_mean.shape)

# 평균을 뺀 절대값이 가장 작은 것 100개를 출력
apple_index=np.argsort(abs_mean)[:100]
fig,axs=plt.subplots(10,10,figsize=(10,10))
for i in range(10):
    for j in range(10):
        axs[i,j].imshow(fruits[apple_index[i*10+j]], cmap='gray_r')
        axs[i,j].axis('off')
plt.show()
# 대부분은 사과입니다.

• 비슷한 샘플끼리 묶는 것이 군집(Clustering)
• 묶인 그룹을 cluster라고 합니다.

k-Means

• 몇 번의 반복으로 데이터 세트를 빠르고 효율적으로 클러스터링 하는 알고리즘
• PCM(Pulse-Code Modulation)을 구현하기 위해서 등장

알고리즘

• 무작위로 centroid를 선정
• 각 데이터들을 각 centroid에 배정
• 배정된 데이터들의 거리가 최소가 되도록 centroid를 수정해서 다시 데이터들을 할당
• centroid가 더 이상 변경되지 않으면 종료

클래스

sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300. tol=0.0001, precomput_distance='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')

• n_clusters: 클러스터 개수
• init 은 군집 중심점의 좌표를 설정하는 방법
• max_iter: 최대 반복 횟수
• 훈련은 fit 이나 fit_transform 함수를 호출
• labels_ 속성에 군집 중심점 레이블을 저장
• clustercenters 속성에 각 군집 중심점 좌표를 소유

임의로 만든 데이터를 가지고 군집 - K-Means 이용

from sklearn.datasets import make_blobs
#중심점의 좌표 와 표준 편차 생성
blob_centers = np.array([[0.2, 2.3], [-1.5, 2.3], 
                         [-2.8, 1.8], [-2.8, 2.8], [-2.8, 1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
#데이터 생성
X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std,
                 random_state=42)
#데이터 확인
def plot_clusters(X, y=None):
    plt.scatter(X[:, 0], X[:, 1], c=y, s=1)
    plt.xlabel("x_1:", fontsize=14)
    plt.ylabel("x_2:", fontsize=14, rotation=0)
plt.figure(figsize=(8,4))
plot_clusters(X)
plt.show()    
#군집 수행
from sklearn.cluster import KMeans
k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)
print(y_pred)
# 각 그룹의 중앙점의 좌표 출력
print(kmeans.cluster_centers_)
#결정 경계를 시각화
#voronoi diagram: 평면을 특정 점까지의 거리가 가까운 점의 집합으로 분할한 그림
#데이터의 분포를 시각화
def plot_data(X):
    plt.plot(X[:, 0], X[:, 1], 'k', markersize=2)       
#중심점을 출력하는 함수
def plot_centroids(centroids, weights=None, circle_color='w', cross_color='k'):
    if weights is not None:
        centroids = centroids[weights > weights.max() / 10   
    plt.scatter(centroids[:, 0], centroids[:, 1], marker='o', s=35,
               linewidths=8, color=circle_color, zorder=10, alpha=0.9)    
    plt.scatter(centroids[:, 0], centroids[:, 1], marker='x', s=2,
               linewidths=12, color=cross_color, zorder=11, alpha=1.0)    
#결정 경계를 그려주는 함수
def plot_decision_boundaries(clusterer, X, resolution=1000, show_centroids=True,
                            show_xlabels=True, show_ylabels=True):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution),
                        np.linspace(mins[1], maxs[1], resolution))    
    Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), cmap='Pastel2')
    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), linewidths=1, 
                color='k')
    plot_data(X)
    if show_centroids:
        plot_centroids(clusterer.cluster_centers_)
    if show_xlabels:
        plt.xlabel("x1", fontsize=14)
    else:
        plt.tick_params(labelbottom=False)
    if show_ylabels:
        plt.xlabel("x2", fontsize=14)
    else:
        plt.tick_params(labelleft=False)      
#결정 경계를 그려주는 함수를 호출
plt.figure(figsize=(8,4))
plot_decision_boundaries(kmeans, X)
plt.show()

K-Means의 문제점

• 데이터를 클러스터에 할당할 때, 거리만을 고려하기 때문에 클러스터의 크기가 많이 다르면, 제대로 동작하지 않을 수 있습니다.
• 클러스터의 크기가 유사할 때 잘 동작합니다.
• 샘플을 하나의 클러스터에 할당하는 방식을 하드 군집(Hard Clustering)이라고 하고, 클러스터마다 샘플에 점수를 부여하는 방식은 소프트 군집(Soft Clustering)이라고 하는데, 이 점수는 샘플과 Centroid 간의 거리가 될 수 도 있고, 유사도 점수 일 수 도 있습니다.

• K-Means 클래스의 transform()을 이용하면 각 샘플과 Centroid 사이의 거리를 반환

#중심점 과 의 거리 확인 - 유클리드 거리
print(kmeans.transform(X_new))
print(kmeans.predict(X_new))
#유클리드 거리 확인
np.linalg.norm(np.tile(X_new, (1, k)).reshape(-1, k, 2) - kmeans.cluster_centers_,
               axis=2)

복잡도

• 샘플 개수와 클러스터 개수, 그리고 차원 개수에 선형
• 일반적으로 가장 빠른 군집 알고리즘

Centroid 초기화

• Centroid 위치를 근사하게 알고 있다면, init 하이퍼 파라미터에 centroid 리스트를 담은 np의 ndarray를 이용해서 지정하고 n_init을 1로 설정
• 하이퍼 파라미터를 설정하지 않으면 랜덤하게 centroid를 설정하게 되는데, 처음 이 값이 잘못설정되면 최적화를 하지 못할 수 있음
• n_init은 centroid를 옮기는 횟수이다.

성능 평가 지표

• 각 샘플 과 가장 가까운 centroid 사이의 평균 제곱 거리로 inertia 라고 합니다.
• inertia_ 라는 속성을 이용해서 확인이 가능하고 score()를 호출하면 inertia를 음수 값으로 반환
• inertia는 거리의 개념이기 때문에 작은 숫자가 잘 만들어진 모델
• sklearn은 높은 점수가 좋다라는 원칙을 가지고 있음

#평가 지표 출력
print(kmeans.inertia_)
print(kmeans.score(X))

K-Means++

• K-Means는 랜덤하게 중심점을 초기화하는데 K-Means++는 성능 향상을 위해서 첫 번째 중심점을 선택한 뒤, 다음 중심점은 거리가 먼 중심점을 선택하는 방식
• sklearn의 KMeans 클래스는 이 방식이 기본이며, 랜덤한 초기화를 하고자 하는 경우에는 init 매개변수를 random으로 설정

속도 개선

• 불필요한 계산을 줄이기 위해서 삼각 부등식을 사용합니다.
  - centroid 사이의 거리를 위한 하한선과 상한선을 유지합니다.
  - 기본적으로 이 방식을 사용하고 있으며 algorithm 매개변수를 full로 설정하면 이전 방식을 사용합니다.
• 기본 K-Means는 전체 데이터 세트를 가지고 centroid를 수정하는 방식을 사용하는데, Mini Batch는 일부의 데이터만을 가지고 centroid를 수정하도록 해서 속도를 3~4배 정도 향상 시킵니다.
• 미니 배치를 사용하고자 하는 경우에는 MiniBatchKMeans를 사용합니다.

%%time
from sklearn.cluster import MiniBatchKMeans
k = 5
miniBatchKMeans = MiniBatchKMeans(n_clusters=k, random_state=42)
y_pred = miniBatchKMeans.fit_predict(X)
print(miniBatchKMeans.inertia_)

클러스터 개수 설정

• 최적의 클러스터 개수를 설정하는 방법은 2가지를 확인해서 수행합니다.
• inertia의 elbow(inertia 값이 급격하게 변하는 지점)을 찾아서 설정

#이너셔를 이용한 최적의 클러스터 개수 찾기
kmeans_per_k = [KMeans(n_clusters=k, random_state=42).fit(X) for k in range(1, 10)]
inertias = [model.inertia_ for model in kmeans_per_k]
print(inertias)
#elbow를 찾기 위해서 시각화
plt.figure(figsize=(8, 4))
plt.plot(range(1, 10), inertias, "bo-")
plt.xlabel("k", fontsize=14)
plt.ylabel("Inertia", fontsize=14)
plt.axis([1, 9, 0, 4000])
plt.show()

• 실루엣 계수를 이용하는 방식 - 이 방법을 권장
  - 샘플의 실루엣 계수는 (b-a)/max(a,b)로 구하는데, a는 동일한 클러스터에 있는 다른 데이터와의 평균 거리이고, b는 가장 가까운 클러스터까지의 평균 거리이다.
  - 범위는 -1 ~ +1 이다.
  - +1에 가까워지면, 자신의 클러스터 안에 잘 속해있고, 다른 클러스터와는 멀리 떨어져 있는 것이다.
  - 0에 가까워지면 경계에 위치한다
  - -1에 가깝다면 샘플이 클러스터에 잘못 할당된 것이다.
  - sklearn.metrics.silhouette_samples(X, labels, metric="euclidean") 함수를 이용해서 데이터 세트 와 각 피처 데이터 세트가 속한 군집 레이블 값을 대입해주면 각 데이터의 실루엣 계수를 리턴
  - sklearn.metrics.silhouette_score(X, labels, metric="euclidean") 함수를 이용하면 실루엣 계수의 평균을 리턴 - np.mean(silhouette_samples)

from sklearn.metrics import silhouette_score
print(silhouette_score(X, kmeans.labels_))
silhouette_scores = [silhouette_score(X, model.labels_) for model in kmeans_per_k[1:]]
print(silhouette_scores)
plt.figure(figsize=(8, 4))
plt.plot(range(2, 10), silhouette_scores, "bo-")
plt.xlabel("k", fontsize=14)
plt.ylabel("Inertia", fontsize=14)
plt.axis([1, 9, 0.5, 0.7])
plt.show()

K-Means의 한계

• 속성의 개수가 많으면 정확도가 떨어짐
• 클러스터의 크기나 밀집도가 원형이 아니면 잘 작동하지 않음

#완전한 원형이 아닌 데이터 생성
from sklearn.datasets import make_moons
X, y = make_moons(200, noise=0.05, random_state=42)
plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')
labels = KMeans(2, random_state=42).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')

13)군집을 이용한 이미지 분할

• 이미지를 세그먼트 여러 개로 분할할 때 사용이 가능
• 복잡한 이미지의 경우는 Deep Learning 의 CNN을 많이 이용하는데 구별해야 할 이미지나 색상이 단순한 경우에는 KMeans 로도 가능

# 군집을 이용한 이미지 분할
#이미지를 읽어와서 출력하기
from matplotlib.image import imread
image = imread('./data/ladybug.png')
print(image.shape)
plt.figure(figsize=(10, 5))
plt.subplots_adjust(wspace=0.05, hspace=0.1)
plt.subplot(231)
plt.imshow(image)
plt.title("원본 이미지")
plt.axis('off')
#색상을 가지고 군집을 수행
X = image.reshape(-1, 3)
kmeans = KMeans(n_clusters=8, random_state=42).fit(X)
#각 픽셀이 속한 클러스터의 중앙 좌표를 저장
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_img = segmented_img.reshape(image.shape)
#print(segmented_img)
segmented_imgs = []
n_colors = [10, 8, 6, 4, 2]
for n_clusters in n_colors:
    print(n_clusters)
    kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(X)
    segmented_img = kmeans.cluster_centers_[kmeans.labels_]
    segmented_imgs.append(segmented_img.reshape(image.shape))
for idx, n_clusters in enumerate(n_colors):
    plt.subplot(232 + idx)
    plt.imshow(segmented_imgs[idx])
    plt.title("{0} colors".format(n_clusters))
    plt.axis('off')
plt.show()

• 흑백 이미지의 경우는 0 ~ 255 사이의 숫자로 하나의 픽셀을 나타내는데 대비를 명확하게 하고자 할 때는 threshold 를 설정하고 0 과 1로 수정해서 사용

군집을 이용한 준 지도 학습

• 군집을 수행한 뒤, 분류 모델을 학습하면 조금 더 나은 성능을 발휘하는 경우가 있음
• 차원 축소 개념을 이용한 분류

#군집을 이용한 차원 축소 후 분류
#8 * 8 크기의 흑백 숫자 이미지 1797 개 가져오기
from sklearn.datasets import load_digits
X_digits, y_digits = load_digits(return_X_y=True)
print(X_digits.shape)
print(y_digits.shape)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits,                                                  random_state=42)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(multi_class='ovr', solver='lbfgs', 
                             max_iter=5000, random_state=42)
log_reg.fit(X_train, y_train)
log_reg_score = log_reg.score(X_test, y_test)
print(log_reg_score)
from sklearn.pipeline import Pipeline
#군집한 클러스터를 속성으로 추가해서 분류를 하기 때문에 성능이 좋아질 가능성이 높음
pipeline = Pipeline([
    ("kmeans", KMeans(n_clusters=50, random_state=42)),
    ("log_reg", LogisticRegression(multi_class="ovr", solver="lbfgs",
                                  max_iter=5000, random_state=42))
])
pipeline.fit(X_train, y_train)
pipeline_score = pipeline.score(X_test, y_test)
print(pipeline_score)
%%time
#최적의 클러스터 개수 찾기
from sklearn.model_selection import GridSearchCV
param_grid = dict(kmeans__n_clusters=range(2, 100))
grid_clf = GridSearchCV(pipeline, param_grid, cv=3, verbose=2)
grid_clf.fit(X_train, y_train)
print(grid_clf.best_params_)
print(grid_clf.score(X_test, y_test))

계층적 클러스터링

개요

• 계층적인 트리로 클러스터를 조직화 하는 방법
• 특이점 또는 비정상적인 그룹이나 레코드를 발견하는데 민감
• 직관적인 시각화가 가능하기 때문에, 클러스터를 해석하기가 용이

용어

• Dendrogram
  - 계층적 클러스터를 시각화 한 것
• Distance
  - 한 레코드가 다른 레코드와 얼마나 가까운지를 보여주는 지표
• Dissimilarity
  - 비유사도
  - 한 클러스터와 다른 클러스터들과 얼마나 가까운지를 보여주는 지표
  

사용하는 경우

• 컴퓨터 자원을 많이 소모하기 때문에 수만 개 정도의 레코드까지만 사용

방법

• 분할 계층 군집
  - 전체 데이터를 하나의 클러스터에 할당하고 더 작은 클러스터로 반복적으로 나누는 방식
• 병합 계층 군집
  - 하나의 데이터를 하나의 클러스터로 만들고 가장 가까운 클러스터를 병합해나가는 방식
  - 구현을 할 때는 가장 비슷한 샘플의 거리를 계산해서 병합할 수 도 있고 가장 먼 거리의 샘플을 이용해서 병합하기도 합니다.

평균 열결과 중심 연결 그리고 와드 연결(군집 내 편차들의 제곱합) 3가지 알고리즘을 이용합니다.

#병합 군집
np.random.seed(42)
variables = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID4']
X = np.random.random_sample([5, 3]) * 10 
df = pd.DataFrame(X, columns=variables, index=labels)
print(df)
#거리 계산
from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')), columns=labels,
                       index=labels)
print(row_dist)
#계층적 클러스터링
from scipy.cluster.hierarchy import linkage
row_clusters = linkage(row_dist, method='complete')
pd.DataFrame(row_clusters, columns=['row label 1', 'row label 2', 'distance', 
                                   'items in cluster'],
            index=['cluster %d' %(i+1) for i in range(row_clusters.shape[0])])
#첫번째 와 두번째는 병합된 클러스터 이름이고 세번째는 거리고 네번째는 아이템 개수
#처음에는 클러스터가 데이터 개수만큼이므로 5개
#1번 클러스터 와 4번 클러스터를 합쳐서 5번 클러스터 생성(데이터 2개)
#0번 클러스터 와 2번 클러스터를 합쳐서 6번 클러스터 생성(데이터 2개)
#3번 클러스터 와 5번 클러스터를 합쳐서 7번 클러스터 생성(데이터 3개)
#6번 클러스터 와 7번 클러스터를 합쳐서 8번 클러스터 생성(데이터 5개)
#덴드로그램 출력
#계층적 군집을 시각화 하는 도구
from scipy.cluster.hierarchy import dendrogram
row_dendr = dendrogram(row_clusters, labels=labels)
plt.show()

GMM (가우시안 혼합 모델)

개요

• 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 Gaussian 분포(정규 분포)에서 생성되었다고 가정하는 확률 모델
• 정규분포
  - 평균이 0이고 표준 편차가 1인 정규분포를 표준 정규 분포라고 하며, 이를 가우시안 분포라고 합니다.
  

클래스

• sklearn.mixture.GaussianMixture
• 가장 중요한 하이퍼 파라미터는 n_components로, 몇 개의 군집을 생성할 것인지 여부를 설정
• 생성 모델이라서 sample 함수를 이용해서 새로운 데이터 생성 가능

#샘플 데이터를 3개의 군집으로 묶기
X1, y1 = make_blobs(n_samples=1000, centers=((4, -4), (0, 0)), random_state=42)
X1 = X1.dot(np.array([[0.374, 0.95], [0.732, 0.598]]))
X2, y2 = make_blobs(n_samples=250, centers=1, random_state=42)
X2 = X2 + [6, -8]
X = np.r_[X1, X2]
y = np.r_[y1, y2]
from sklearn.mixture import GaussianMixture
gm = GaussianMixture(n_components=3, random_state=42)
gm.fit(X)
#중심점의 좌표
print(gm.means_)
#예측
print(gm.predict(X))
#확률
print(gm.predict_proba(X))
#생성
X_new, y_new = gm.sample(6)
print(X_new)
print(y_new)