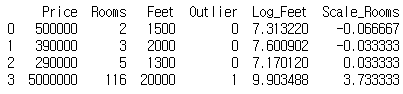수업 35일차

✔ 데이터 전처리

숫자 데이터

단위 환산

• 여러 곳에서 데이터를 수집하는 경우, 단위가 달라서 발생할 수 있는 문제를 해결하기 위해서 수행

❗ 표준화 - Standardization

• 다변량 분석(분석의 대상이 되는 컬럼이 2개 이상)의 경우에는 숫자 데이터의 상대적 크기 차이 때문에 분석 결과가 왜곡이 될 수 있다.
• 상대적으로 큰 숫자 값을 갖는 컬럼의 영향이 커지게 된다.
• 각 컬럼의 값을 동일한 크기 기준으로 나눈 비율로 나타내는 것을 표준화 라고 하는데, Scaling이라고도 합니다.
• 표준화를 거치게 된다면, 데이터는 0 ~ 1 또는 -1 ~ 1 사이의 값을 갖게 됩니다.
• 직접 연산을 수행하는 경우는 최대값으로 나눈 비율이나 자신의 값에서 최소값을 뺀 값으로 나누는 방식을 이용합니다. (0 ~ 1), 보간검색?
• 표준 값 : (데이터 - 평균) / 표준 편차
• 편차 값 : 표준값 * 10 + 50
  - 이렇게 된다면, 표준값의 평균은 0, 표준 편차는 1
  - 편차 값의 평균은 50, 표준 편차는 10
  - 표준 점수(값) 0.0 이상은 전체의 50%
  - 1.0 이상은 전체의 15.866%
  - 2.0 이상은 전체의 2.275%
  - 3.0 이상은 전체의 0.13499%
  - 4.0 이상은 전체의 0.00315%
  - 5.0 이상은 전체의 0.00002%

실습

• 기본 import

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
# 한글 출력을 위한 설정
from matplotlib import font_manager, rc
import platform
if platform.system()=='Darwin':
    rc('font', family='AppleGothic')
elif platform.system()=='Windows':
    font_name=font_manager.FontProperties
    (fname='c:/Windows/Fonts/malgun.ttf').get_name()
    rc('font', family=font_name)
# 음수 사용(마이너스 기호 깨짐 방지)
plt.rcParams['axes.unicode_minus'] = False

• Data Load

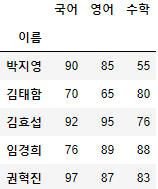
# 기본 키로 사용할만 한 것이 있다면 인덱스로 하자.
# 여기서는 이름으로 해보겠습니다.
df=pd.read_csv('./data/student.csv',encoding='cp949',index_col='이름')
df.head()
# 해당 데이터는 단순한 표준화 작업만으로는 성적을 비교하는 것이 
#어려울 수 있습니다. 
# 최대값이나, 최대값-최소값으로 나눈 데이터로는 비교하기가 어렵습니다.
# 세 과목은 절대적 크기의 범위가 같다. 
# 그렇다면 max, max-min 으로는 비교하기가 어렵다.
# 바로, '난이도' 를 확인해야 한다.
# 이에 좋은 것은 바로 '표준편차' 입니다.
# 표준 값이나 편차값을 구해서 비교하는 것이 좋습니다.

---

• 과연, 경희는 수학보다 영어를 잘 본 편인걸까?
• '난이도' 의 영향을 생각해야 한다.

---

• 우선 그래프로 확인을 해보자.

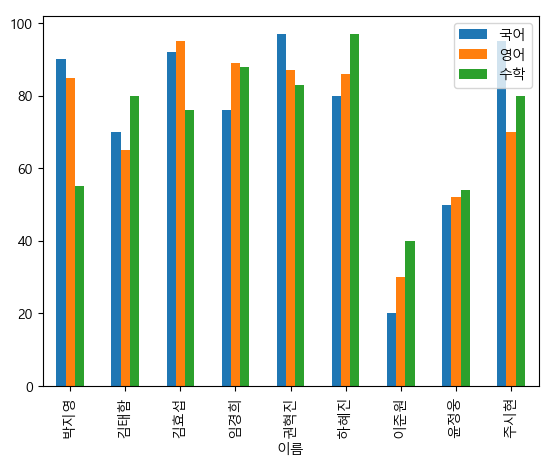
df.plot.bar()
df.plot(kind='bar')
# 둘 중 하나를 쓰자.

• 단순 수치 값의 비교는 가능하다.
• 이렇게 본다면, 경희는 수학보단 영어를 잘 본 것이다.

---

• 표준값, 편차값으로 그래프를 그려봅시다.

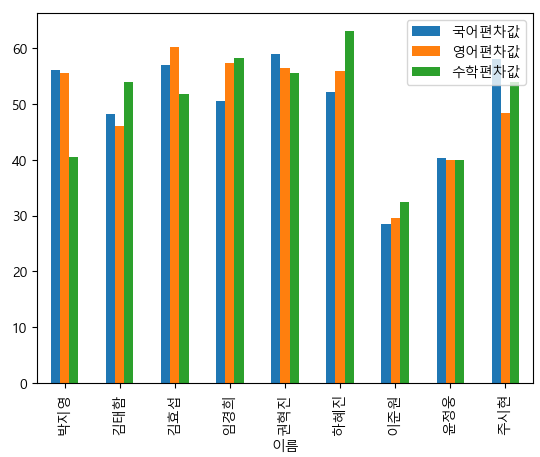
# 평균과 표준편차를 알아야 합니다.
kormean, korstd=df['국어'].mean(), df['국어'].std()
engmean, engstd=df['영어'].mean(), df['영어'].std()
matmean, matstd=df['수학'].mean(), df['수학'].std()
# 표준 값을 구합니다.
df['국어표준값']=(df['국어']-kormean)/korstd
df['영어표준값']=(df['영어']-engmean)/engstd
df['수학표준값']=(df['수학']-matmean)/matstd
# 편차값 구하기
df['국어편차값']=df['국어표준값']*10+50
df['영어편차값']=df['영어표준값']*10+50
df['수학편차값']=df['수학표준값']*10+50
# 이 친구들로 그래프를 그려보자.
df[['국어편차값', '영어편차값','수학편차값']].plot(kind='bar')

• 해당 그래프를 본다면, 경희의 수학 편차값이 영어 편차값보다 높은 것을 알 수 있다.

실습 - auto_mpg

# 데이터 읽어오기
auto_mpg=pd.read_csv('./data/auto-mpg.csv', header=None)
# 컬럼 이름 설정하기
auto_mpg.columns=['mpg', 'cylinders', 'displacement',
'horsepower', 'weight','acceleration', 'model year', 'origin','name']
auto_mpg['horsepower'].replace('?',np.nan,inplace=True)
auto_mpg.dropna(subset=['horsepower'],axis=0, inplace=True)
auto_mpg['horsepower']=auto_mpg['horsepower'].astype('float')
auto_mpg.head()

• horsepower 열을 표준화 해보자.
• max와 min의 차이를 봐볼까?

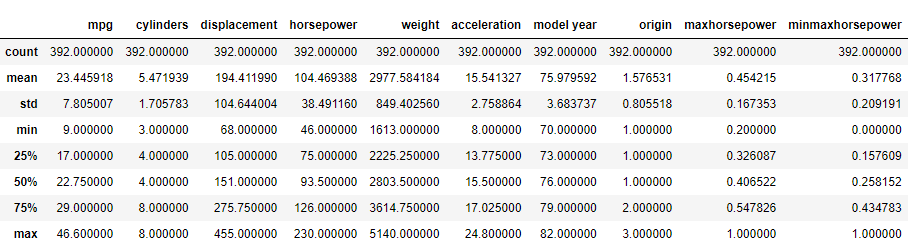
# horsepower 열의 표준화
auto_mpg['maxhorsepower']=auto_mpg['horsepower']/
auto_mpg['horsepower'].max()
auto_mpg['minmaxhorsepower']=(auto_mpg['horsepower']-
auto_mpg['horsepower'].min())/
(auto_mpg['horsepower'].max()-auto_mpg['horsepower'].min())
auto_mpg.describe()

• 새로 만든 maxhorsepower와 minmaxhorsepower의 max와 min 값을 보면, max는 같지만 min은 다른 것을 확인할 수 있다.

사이킷 런의 표준화 클래스

• StandardScaler
  - 평균이 0이 되고, 표준편차가 1이 되도록 변환
  - (벡터-평균)/표준편차
  - 주성분 분석(PCA - 차원 축소를 목적으로 하는 비지도 학습) 이나, 성적처럼 값의 범위가 동일한 데이터를 비교하고자 할 때 사용합니다.

• MinMaxScaler
  - 최대값이 1이고 최소값이 0이 되도록 변환
  - 신경망에서 주로 이용합니다.
  - (벡터 - 중간값) / (최대값 - 최소값)

• RobustScaler
  - 중간값(median)이 0이 되고 IQR이 1이 되도록 변환
  - 중간값과 사분위 범위를 사용하여 스케일을 조정합니다.
  - (벡터 - 중간값) / (75%값 - 25%값)
  

• MaxAbsScaler
  - 0을 기준으로 절대값이 가장 큰 수가 1또는 -1이 되도록 하는 표준화
  - 절대값이 0 ~ 1이 되도록 하는 방법
  - 각 컬럼 별로 절대값이 가장 큰 데이터로 나누는 방식입니다.
  

• QuantileTransformer
  - 데이터를 1000개의 분위로 나누어서 0 ~ 1 사이에 고르게 분포시키는 방법
  - 이상치로 인한 영향을 줄여주는 방식입니다.

  ---

• StandardScaler와 RobustScaler의 경우는 대부분 표준화된 형태의 데이터 분포로 변환합니다.

• MinMaxScaler는 특정 값에 집중되어 있는 데이터가 그렇지 않은 데이터 분포보다 표준 편차에 의한 스케일 변화 값이 커지게 되어서 한쪽으로 쏠림 현상이 있는 데이터의 분포의 경우는 형태를 거의 유지합니다.

• MaxAbsScaler는 음수와 양수 데이터가 섞여있는 경우에는, 어느정도 대칭 분포를 유지합니다.

---

• 스케일링을 할 떄는 outlier에 대해 고민을 해야 합니다.
• 분포에 대한 고민도 같이 해야 하는데, 분포를 그대로 유지시키지 않고 모든 컬럼들의 분포를 유사하게 만드는 경우에는 한쪽으로 쏠린 데이터의 경우는 작은 차이가 아주 큰 변화를 가져오기도 합니다.
• 스케일링을 하기 전에 각 컬럼의 분포를 확인한 후 하는 것이 좋습니다.
• 하는 방법은 데이터를 입력으로 해서 fit 메서드를 호출하면, 분포 모수를 객체 내에 저장하고, 데이터를 입력으로 해서 transform 메서드를 호출하면 데이터를 변환합니다.
  - 2개의 과정을 합쳐서 fit_transform 메서드를 호출해도 됩니다.

• 스케일링 시 주의할 점은 스케일링의 대상은 numpy의 ndarray입니다.

atuo_mpg - 사이킷런 이용해서 전처리, 표준화 스케일링 작업

from sklearn import preprocessing
# 스케일링을 수행할 데이터 가져오기
x=auto_mpg[['horsepower']].values
# print(type(x))
print('평균', np.mean(x))
print('표준편차', np.std(x))
print('최대값', np.max(x))
print('최소값', np.min(x))
scaler=preprocessing.StandardScaler()
scaler.fit(x)
x_scaled=scaler.transform(x)
print('평균', np.mean(x_scaled))
print('표준편차', np.std(x_scaled))
print('최대값', np.max(x_scaled))
print('최소값', np.min(x_scaled))

• 이에 대한 결과는

평균 104.46938775510205
표준편차 38.44203271442593
최대값 230.0
최소값 46.0
- - - - 스케일링 이후 - - - - 
평균 -1.812609019796174e-16
표준편차 0.9999999999999998
최대값 3.2654519904664348
최소값 -1.5209754434541274

• StandardScaler 말고 다른 것도 사용이 가능하다.

정규화(Normalize)

• 데이터의 범위를 0 과 1 사이로 변환하여 데이터의 분포를 조정하는 것
• Scaler는 각 컬럼의 통계 데이터를 이용해서 수행하지만, Normalizer는 행 단위로 스케일링을 합니다.
• 여러가지 연관된 컬럼을 가진 데이터(텍스트)에서 많이 사용
• Normalizer 클래스의 함수를 이용해서 수행하는데, norm옵션에 l1을 대입한다면 맨하튼 거리로 계산하고, l2로 대입하면 유클리드 거리로 계산하고 max를 설정하면 가장 큰 값으로 나눕니다.

• 유킬리드 거리는 값을 각 데이터를 제곱해서 더한 값의 제곱근으로 나누는 것, 맨하튼 거리는 값을 각 데이터의 합으로 나눈 것
• 정규화 작업을 할 때는 fit함수를 호출하지 않고 바로 transform을 호출합니다.

다항 특성과 교차항 특성

• 다항은 데이터들을 곱하고 제곱해서 데이터를 추가하는 것
• 특성과 타겟 사이에 비선형 관계가 존재하는 경우에 다항 특성을 생성
• 질병은 일정한 패턴으로 발생하지 않고 나이가 많을 수록 질병에 걸릴 확률이 높아진다.
  - 이런 경우에는 단항으로만 분석하는데는 한계가 존재함
  - 특성에 변동 효과를 주입해서 분석
  - 다른 특성이 영향을 주는 경우에는 각 특성을 곱한 교차항을 추가합니다.
• sklearn.preprocessing.PolynomialFeatures 클래스를 이용하는데, degree 옵션에 몇 차 항까지 생성할지 여부를 설정하고 include_bias 옵션으로 첫 번쨰 항에 상수 1을 추가할 지 여부를 설정, interatcion_only를 true로 설정한다면 교차항 특성만 생서합니다.

[2,3]
PolynomialFeatures(degree=2, include_bias=True)
->
[1,2,3,4,6,9], interaction_only true면 4랑 9 제거,
degree가 3이라면 여기에 8, 27 추가

features=np.array([[1,2],[2,3],[3,8],[4,2],[7,2]])
# 제곱 항까지의 다항을 생성 - 열의 개수가 늘어남
# 회귀 분석을 할 때, 시간의 흐름에 따라
# 변화가 급격하게 일어나는 경우 또는
# 데이터가 부족할 때 샘플 데이터 추가를 위해 사용합니다.
# 제곱을 하거나 곱하기를 하게 된다면 
# 데이터의 특성 자체는 크게 변화하지 않기에 사용
polynomialer=preprocessing.PolynomialFeatures(degree=2)
result=polynomialer.fit_transform(features)
print(result)

---

특성 변환

• 데이터에 함수를 적용하는 것
• sklearn의 FunctionTransformer(동일한 함수 적용)와 ColumnTransformer(컬럼마다 다른 함수 적용 가능)를 이용
• pandas.apply가 동일한 기능을 갖습니다.
• numpy나 머신 러닝 패키지의 작업 단위는 numpy의 ndarray이고, pandas는 Series나 DataFrame 입니다.
• pandas는 데이터를 가져오는 함수가 많이 제공되기에, pandas를 이용해서 데이터를 가져온 후, numpy의 ndarray로 변환해서 사용하자.

features=np.array([[1,2],[2,3],[3,8],[4,2],[7,2]])
# 위의 데이터에 함수를 적용해보자.
# 간단하게 한다면 lambde를 사용하면 된다.
result1=preprocessing.FunctionTransformer(lambda x: x+1).
transform(features)
print(result1)
# pandas에서는 이렇게 하면 됩니다.
df=pd.DataFrame(features,columns=['feature1', 'feature2'])
print(df.apply(lambda x: x+1).values)

• 이번엔 컬럼 별로 다른 함수를 적용해보자.

from sklearn.compose import ColumnTransformer
features=np.array([[1,2],[2,3],[3,8],[4,2],[7,2]])
df=pd.DataFrame(features,columns=['feature1', 'feature2'])
# 컬럼 별로 다른 함수를 적용해보자.
def add_one(x):
    return x+1
def sub_one(x):
    return x-1
result2=ColumnTransformer([("add_one",
preprocessing.FunctionTransformer(add_one, validate=True),
['feature1']),
("sub_one",preprocessing.FunctionTransformer(sub_one, validate=True),
['feature2'])]).fit_transform(df)
print(result2)

• 튜플 형태로 넣어준다.

이산화

• 연속형 변수를 일정한 구간으로 나누고, 각 구간을 범주형 이산 변수로 치환하는 과정
• 구간을 분할한다고 해서 구간 분할(binning)이라고 하기도 합니다.
• 가격이나 비용, 또는 효율 등의 데이터에 많이 적용합니다.
• 방법
  - pandas의 cut 함수 이용
  - numpy의 digitize 이용
  - sklearn의 Binarizer와 KBinsDiscretizer 클래스 이용

  ---

  - 아니면 군집 분석을 이용(Clustering - 여러 데이터를 그룹 별로 나누는 비지도 학습의 일종)
  • 많은 양의 데이터가 있다면, 분석을 하는 것은 많은 시간을 소모해서 위의 패키지를 이용하는 것이 훨씬 좋다.

• 지도학습 : 레이블이 존재하는 상황에서의 학습
  - 딥러닝은 지도 학습의 일종
• 비지도학습 : 레이블이 없어서 레이블을 만들어야 하는 학습
• 강화학습 : 보상이 주어지는 학습

• pandas의 cut 이용
  - x 옵션에 데이터를 설정
  - bins에 경계값의 list - 첫 번째 데이터가 첫 구간의 시작값
  - lables 에 각 그룹의 이름을 설정
  - include_lowe에 첫 경계값 포함 여부를 설정

# auto_mpg의 horsepower를 3개의 구간으로 분할
# auto_mpg['horsepower'].describe()
# 경계값 찾기
count, bin_dividers=np.histogram(auto_mpg['horsepower'],bins=3)
print(count, bin_dividers)
# 각 그룹에 할당할 값의 리스트
bin_names=['저출력', '보통출력', '고출력']
auto_mpg['hp_bin']=pd.cut(x=auto_mpg['horsepower'],
bins=bin_dividers, labels=bin_names, 
include_lowest=True)
auto_mpg[['horsepower','hp_bin']].head(20)

• bin_dividers 를 출력해봐야 합니다.
• [ 46. 107.33333333 168.66666667 230. ] 총 3개 구간이다. 첫 가운데 끝

• numpy의 digitize 함수
  - 첫 번째 매개변수로 이산화할 데이터
  - bins에 경계값의 list - 첫 데이터가 첫 구간의 끝(?????)
  - right에 경계값 포함 여부 설정

# numpy에서는 그룹의 명칭을 설정하지 않고 0, 1, 2, ... 인덱스로 구분합니다.
result=np.digitize(auto_mpg['horsepower'], 
bins=[107.33333333,168.66666667,230.0], right=True)
print(result) # 그룹의 이름이 없음

• sklearn 이용
  - Binarizer : 하나의 임계값을 설정해서 0과 1, 2개의 그룹으로 분할할 때 사용(참 / 거짓)
  - KBinsDiscretizer : 여러 개의 임계값을 설정해서 분할
  • encode 옵션에 ordinal : 일련번호 형태로, onehot은 원 핫 인코딩으로 희소 행렬, onehot_dense면 one-hot-encoding으로 밀집 행렬 리턴
  • strategy 옵션에 quantile(각 구간의 개수를 유사하게), uniform(구간의 크기를 유사하게)을 설정
  • 각 구간의 경계깞을 알고자 하는 경우에는 bin_edges_ 속성을 호출하자
• sklearn이 업데이트 되면서, 속성을 직접 리턴하던 것을 함수로 변경하는 경우가 종종있습니다.
• 이름 뒤의 under_bar
• one-hot encoding(용어기억) : 하나의 데이터를 하나의 열로 표현하는 것

# sklearn의 binning(구간 분할)
age=np.array([[13],[30],[67],[36],[20],[33],[27],[19]])
# 2개 그룹으로 분할
binarizer=preprocessing.Binarizer(threshold=30.0)
result=binarizer.transform(age)
print(result)
# 여러 개의 그룹으로 분할
# 4개의 그룹으로 분할하기
# strategy를 uniform으로 설정하면 간격을 일정하게 분할함
# encode가 ordinal이면 "일련번호" 로 그룹이 생성
# onehot을 설정하면 one hot encoding을 하고 희소행렬로 보여준다.
# onehot-dense로 설정하면 onehote encoding을 하고 밀집 행렬로 보여준다.
kb=preprocessing.KBinsDiscretizer(4,encode='ordinal',
strategy='quantile')
result2=kb.fit_transform(age)
print(result2)

from sklearn.cluster import KMeans
sample=np.array([[13,30],[30,40],[67,44],[26,24],[22,11],[98,28]])
df=pd.DataFrame(sample,columns=['feature_1','feature_2'])
#3개의 군집으로 분할하는 객체 생성
cluster=KMeans(3,random_state=42)
#sample 데이터를 이용해서 훈련
cluster.fit(sample)
#sample 데이터를 가지고 예측
df['group']=cluster.predict(sample)
print(df)

이상치(Outlier) 감지

• z 점수를 이용하는 방법
  - 중앙값을 기준으로 표준편차가 3또는 -3 범위의 바깥족에 위치하는 데이터를 이상치로 간주하는 방법
• z 점수를 보완해서 적용하는 방법(중위 절대 편차)
  - z 점수는 데이터가 12개 이하이면 이상치를 감지하지 못하는데, 이를 보완하기 위해서 표준편차의 범위를 3.5로 늘리고, 이 값에 0.6745를 곱한 범위 바깥의 데이터를 이상치로 간주
• IQR(3사분위수-1사분위수)을 이용하는 방법
  - 1사분위수보다 1.5 IQR 이상 작은 값이나 3사분위수 보다 1.5 IQR 이상 큰 데이터를 이상치로 간주
  - boxplot이 이 방법으로 이상치를 출력
• 3가지 모두를 적용해서 2개 이상에서 이상치로 간주된다면 이상치로 판정하는 방법

---

• sklearn.covariance 패키지의 EllipticEnvelope 객체를 이용해서 이상치를 검출할 수 있는데, 이 객체는 일정한 이상치 비율을 설정해서 이상치를 감지합니다.

# z-score를 이용해서 이상치를 판별해주는 함수
# z-score를 이용해서 이상치를 판별해주는 함수
def outlier_z_score(ys):
    #표준편차 임계값
    threshold=3
    mean_y=np.mean(ys)
    print("평균", mean_y)
    std_y=np.std(ys)
    print("표준편차", std_y)
    z_scores=[(y-mean_y)/std_y for y in ys]
    print("z_score", z_scores)
    print('\n')
    return np.where(np.abs(z_scores)>threshold)
features=np.array([[10,10,7,6,3,1,2],[223232,3,23,12,11,1,2]])
print(outlier_z_score(features))

• (array([1], dtype=int64), array([0], dtype=int64)) 이라고 알려준다. 하지만 데이터 개수가 적다면?

# z-score를 이용해서 이상치를 판별해주는 함수
def outlier_z_score(ys):
    #표준편차 임계값
    threshold=3.5
    # 이제 평균이 아닌 중앙값
    mean_y=np.median(ys)
    # 표준편차도 단순 표준편차가 아닌 그 중앙값임
    std_y=np.median([np.abs(y-mean_y) for y in ys])
    z_scores=[0.6745*(y-mean_y)/std_y for y in ys]
    return np.where(np.abs(z_scores)>threshold)
#이렇게 처리해준다면 데이터가 적어도 이상치 탐지를 할 수 있다.
features=np.array([[10,10,7,6,3],[223232,3,23,12,11]])
print(outlier_z_score(features))

• 편차가 높을 때는 중앙값을 사용하고, 편차가 낮을 때는 평균을 사용합니다.
• 왜냐하면, 평균은 이상치에 영향을 받기 때문입니다. (중앙값은 영향 x)

• 데이터의 갭이 크거나 데이터의 개수가 너무 작으면 보정한 z_score를 사용하고, 데이터의 갭이 크지 않거나 데이터의 개수가 많다면 z-score를 사용해도 무방합니다.
• IQR(3사분위수-1사분위수)를 사용하는 이유도 같은 이유입니다.

• boxplot이 이상치를 표현하는 방법

# IQR을 이용하는 방법
def outliers_iqr(ys):
    # 1사분위 수와 3사분위 수 구하기
    quartile_1, quartile_3=np.percentile(ys,[25,75])
    iqr=quartile_3-quartile_1
    #일반적인 데이터의 하한과 상한을 구하기
    lower_bound=quartile_1-(iqr*1.5)
    upper_bound=quartile_3+(iqr*1.5)
    return np.where((ys>upper_bound)|(ys<lower_bound))
features=np.array([[10,10,7,6,3],[223232,3,23,12,11]])
print(outliers_iqr(features))

# 일정 비율의 데이터를 이상치로 간주하기
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs
features, _=make_blobs(n_samples=10, n_features=2, 
centers=1, random_state=42)
# print(features)
# 데이터 이상치 탐지를 위해 변경
features[0,0]=10000
features[0,1]=10001
print(features)
# 이상치 감지 객체를 생성 - 이상치 비율을 설정하자
outlier_detector=EllipticEnvelope(contamination=0.1)
outlier_detector.fit(features)
# 이상치로 판별된다면 -1 리턴, 아니면 1 리턴
outlier_detector.predict(features)

이상치 처리 방법

• 데이터를 삭제
  - 현실적으로 거의 발생할 수 없는 데이터인 경우에만
• 이상치로 표시하고 이를 특성의 하나로 포함
  - 최근의 날씨 같은 경우
• 이상치의 영향이 줄어들도록 특성을 변환 - scailing
  - 데이터의 편차를 줄이는 방법을 이용해서 이상치의 영향을 최소화
  - 이상치의 영향을 줄여야 하므로 RobustScaler 사용을 권장합니다.

# 이상치 처리
houses=pd.DataFrame()
houses['Price']=[500000,390000,290000,5000000]
houses['Rooms']=[2,3,5,116]
houses['Feet']=[1500,2000,1300,20000]
# Rooms>20 이면 이상치로 간주하고 특성을 추가하겠습니다.
houses['Outlier']=np.where(houses['Rooms']>20,1,0)
print(houses)

• 지운게 아니라, 특성으로 추가를 하였습니다.

# Outlier의 영향을 최소화 - 특성 변환(로그 변환)
houses['Log_Feet']=[np.log(x) for x in houses['Feet']]
print(houses)

• 기존 20000 : 1300 보다는 비율이 훨씬 줄어들어서 영향을 최소화한다.

# 더 영향을 줄인다 - 특성 변환 (Scailing)
imsi=pd.DataFrame(houses['Rooms'])
scaler=preprocessing.RobustScaler()
scaler.fit(imsi)
houses['Scale_Rooms']=scaler.transform(imsi)
print(houses)

• 3.5 넘어가는 이쁜 이상치이다.

결측치

• 존재하지 않는, 아직 알려지지 않은 값
• python 에서는 None, numpy에서는 numpy.NaN, pandas에서는 '', '#N/A', 'NULL', 'NaN' 등의 문자열을 None으로 인식
• pandas에서는 rad 메서드들의 na_values라는 옵션이 있는데, 이는 None으로 간주할 데이터의 list를 설정하는 옵션입니다.

---

• 결측치 확인 방법
  - DataFrame에서는 info 함수로 확인 가능
  - RangeIndex는 전체 데이터의 인덱스 개수이고 각 열의 데이터 개수와 비교해서 일치하면 None,이 없는 것이고 아니면 None이 존재하는 것임
  - 열의 데이터 개수를 확인할 때, value_counts()함수에 dropna=False 추가해서 None의 개수를 확인
  - isnull과 notnull 함수를 이용해서 확인하는 것이 가능

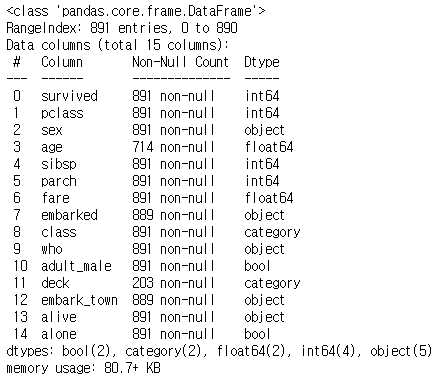
# 결측치 확인
import seaborn as sns
titanic=sns.load_dataset('titanic')
titanic.info()

• rangeindex는 891이다.
• info 값을 확인 했을 때, 714, 889, 203 등... 이들은 결측치가 있는 것이다.

---

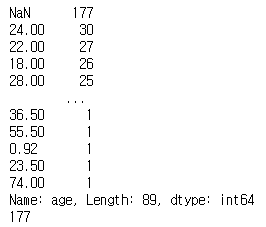
# 결측치 확인
# none의 개수도 출력
print(titanic['age'].value_counts(dropna=False))
# isnull 이용하기
print(titanic['age'].isnull().sum(axis=0))

• 여러 방법으로 확인할 수 있다.

결측치 처리

• 결측치의 비율이 높은 열의 경우는 열을 제거
• 결측치의 비율이 높지 않은 경우는 행을 제거 - 최후의 수단
  - DataFrame의 경우는 dropna 함수 이용
• 결측치를 다른 값으로 대치
  - DataFrame의 경우는 fillna 함수를 이용해서 이전 값이나 이후 값, 또는 limit을 이용해서 대치하는 개수를 설정하는 것이 가능합니다.
  - 아니면 replace 함수를 이용

결측치 처리 시 주의사항

• 머신러닝 알고리즘은 결측치를 처리할 수 없습니다.
  - 머신러닝을 할 때는 결측치가 존재하면 안됩니다.
• 행 삭제는 항상 주의해야 합니다.
  - 해당 데이터의 다른 정보를 얻을 수 없게 되어서, 데이터의 편향이 늘어날 수 있기 때문입니다.
  

결측치 종류

• MCAR(Missing Completely At Random)
  - 값이 누락될 확률이 모든 것에 독립적인 경우
• MAR(Missing At Random)
  - 값이 누락될 확률이 완전히 랜덤하지는 않고 다른 특성의 정보에 의존하는 경우
• NMAR(Not Missing At Random)
  - 다른 정보에 의존을 하는 경우
  - ex) 스타벅스에서 상품 구매 여부를 묻고 추천하고자 하는 상품을 묻는 경우
• MCAR이나 MAR은 데이터를 삭제해도 되지만, NMAR은 데이터를 삭제하지 않고 사용하는 경우가 많습니다.

# 결측치 삭제
# 각 컬럼의 None의 개수 파악
print(titanic.isnull().sum(axis=0))
# 결측치의 개수가 200개 미만인 컬럼만 필터링
result=titanic[['survived','pclass','sex','age','sibsp']]
# 결측치인 행만 제거 - age행이 결측치인 행을 제거
result_age=titanic.dropna(subset=['age'], how='any', axis=0)
result_age.info()

결측치 대체

• pandas의 fill_na를 이용해서 값을 채우는 방법
• sklearn의 SImpleImputer를 이용해서 평균이나 중간값 또는 최빈값이나 상수로 채우는 것
• 회귀분석을 이용해서 값을 예측해서 채우는 것
  - 가장 좋은 방법으로 알려져 있지만, 데이터가 많은 경우 회귀 분석을 하는데 시간이 많이 걸리 수 있음
  

titanic=sns.load_dataset('titanic')
# None을 포함하고 있는 값을 출력해보자.
# print(titanic['embark_town'][825:831])
# embark_town 컬럼의 특성이 계절성을 갖는다면, 
# 이경우는 앞의 값으로 채우는 것도 나쁘지 않다.
titanic['embark_town'].fillna(method='ffill', inplace=True)
print(titanic['embark_town'][825:831])
# 결측치가 몇 개 되지 않을 때는 대표값으로 대체
# 대표값으로 사용될 수 있는 데이터는 평균, 중간값, 최빈값 등..
# 대표값으로 변환하는 경우, 많은 양의 데이터를 변경하면
# 분석할 때 결과가 왜곡될 수 있습니다.

titanic=sns.load_dataset('titanic')
mode=titanic['embark_town'].value_counts()
# 가장 많이 출현한 데이터
print(mode)
print(mode.idxmax())
titanic['embark_town'].fillna(mode.idxmax(),inplace=True)
print(titanic['embark_town'][825:831]) 
# 이번엔 829번이 Southampton으로 바뀐 것을 확인할 수 있다.

• sklearn의 클래스를 이용

# sklearn 의 SimpleImputer 이용해보자.
# 객체를 만들 때 strategy 옵션에 
# mean, median, most_freqeunt, constant 를 설정
# constant를 설정하면, fill_Value 옵션에
# 채울 값을 추가해주어야 합니다.
from sklearn.impute import SimpleImputer
features=np.array([[100],[200],[300],[400],[500],[np.nan]])
simple_imputer=SimpleImputer(strategy='median')
print(simple_imputer.fit_transform(features))

• 회귀분석을 통해서 다른 특성과의 연관 관계를 파악해서 데이터를 채우는것
  - 가장 좋다고 알려져 있지만, 데이터가 많으면 시간이 오래 걸립니다.

!pip intall fancyimpute
from fancyimpute import KNN
features=np.array([[100,200],[200,400],[300,600],
[400,800],[200,np.nan]])
print(KNN(k=5,verbose=0).fit_transform(features))

✔ 한글 형태소 분석을 위한 시스템 준비

• JDK 는 한글 형태소 분석을 할 때, 형태소 분석 라이브러리가 자바로 만들어져 있어서 JDK를 설치해야만 사용이 가능합니다.

JDK 설치

• 걍 받아서 설치(오라클, os 맞춰서)
• JAVA_HOME이라는 환경변수를 만들어서 jdk 설치된 디렉(bin 앞에까지)을 등록하고 path 환경변수에 bin 디렉 경로를 추가하자.
• 이후 cmd에서 java -version(JRE버전), javac -version(JAVA 컴파일러) 가 잘나오는지 확인해보자.

C++ buildtools

c++이용한 데스크톱 어쩌구 만 체크하고 설치하면 됩니다.

✔ Git Branch 작업

Branch

• Repository 내의 별도의 독립적인 공간
• 서로 다른 버전의 코드를 만들 때, 서로의 작업에 영향을 주지 않기 위해서 생성
• 생성은 github에서 해도 되고, local git에서 해도 됩니다.
• 원격 저장소에서 만든 branch를 가져올 때는 git remote update를 수행

현재 작업 디렉토리를 원격 git에 upload

• 로컬에서 수행

• git init
• git add .
• git commit -m "message"

• git hub에서 repo 생성 후 url 복사

• git remote add origin url
• git remote -v (확인)
• git push origin main
  - main : branch 이름(github의 기본 branch 이름임)

• branch를 만들고 바꾸려면?

• git branch (branch 확인)
• git branch 새 이름
• git checkout 새브랜치이름
• git push origin localbranch
  - 이러면 localbranch로 하나 올라감
• 삭제 : git branch -d <로컬 브랜치 이름>

• 이렇게 branch가 여러개가 생겨난 것을 확인할 수 있다.

기존 브랜치와 다른 브랜치의 내용이 다른 경우 merge

• fast-forward
  - 기준 브랜치에서 commit한 후 변경 내용이 없는 상태에서 다른 브랜치가 수정된 경우로 바로 반영
  - 기준 브랜치에서 git merge 브랜치이름
  
• merge-commit
  - 기준 브랜치에서 pull을 한 후 기준 브랜치도 새로운 commit을 하고 복사한 브랜치에서도 commit한 경우로 이경우는 auto merging을 실패합니다.
  - 이 경우에는 기준 브랜치에서 먼저 git add 명령으로 변경된 파일을 반영하고 git commit을 하고 다시 merge 하면 됩니다.