[ICML2017]On Calibration of Modern Neural Networks - [2022.07.20]

Model Calibration이란 무엇일까 ?

Calibration : 교정

모델 교정.

보통 교정은 잘못된 행동을 고치거나 바로잡는 것을 뜻한다. 말 그대로 모델의 잘못된 부분을 바로잡는 것이 model calibration이다.

실제 데이터(real-world)에서 분류 신경망 같은 경우 정확할 뿐만 아니라, 예측이 틀렸을 가능성에 대해서도 언급해줄 수 있어야 한다. 예를 들어, 자율 주행 자동차에서 네트워크가 보행자와 다른 장애물들을 탐지한다고 생각해보면, 만약 네트워크가 장애물들에 대해 즉각적으로 탐지하지 못한다면, 부딪힐 것이다.

구체적으로, 네트워크는 calibrated confidence measure를 예측에 추가적으로 제시해야 한다. 다른 말로, 예측 클래스들에 대한 확률값들이 실제 데이터를 얼만큼 맞추느냐를 반영해야 한다는 것이다.

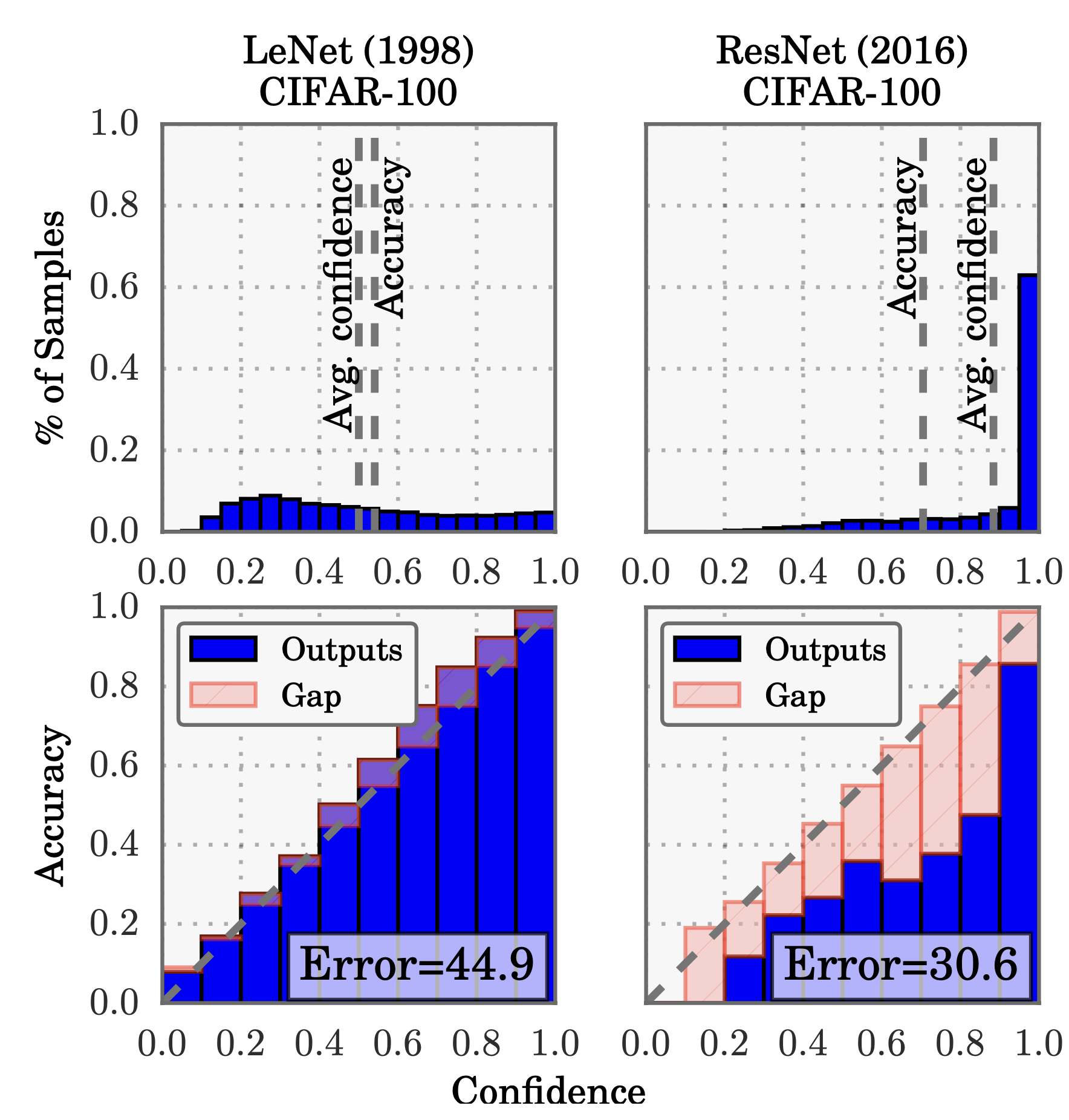
위 그림에서 위쪽 행은, 예측 확률 값에 분포를 보여준다. 평균 Confidence는 LeNet이 accuracy와 얼추 맞는 것으로 보이지만, ResNet의 경우 Accuracy에 비해 Confidence값이 많이 높다. 이는 아래 행을 봤을 때 더 확연히 구분 되는데, LeNet의 경우 well-calibrated 되었다고 말할 수 있다(Confidence가 Accuracy와 비슷하게 잘 맞음). 반면에 ResNet는 Accuracy에 비해 Confidence가 많이 낮다.

본 저자의 목표는 왜 신경망이 miscalibrated되었는지, 그리고 어떤 방법으로 이를 해결할 수 있는지에 대해 알아보는 것이다.

이를 위해 이 논문에서는, 여러 Computer vision과 NLP에서 이를 실험한다. 덧붙여, 훈련과정과 모델 구조의 트렌드가 miscalibration을 발생시킬 수 있음을 시사한다. 마지막으로 여러 후처리 calibration 방법으로 SOTA를 찍는다.

temperature-scaling이 놀라운 효과를 보여준다.

Definitions

먼저 문제를 정의한다.

이 문제는 Supervised Multiclass classification에서 발생하는 문제들을 다룬다.

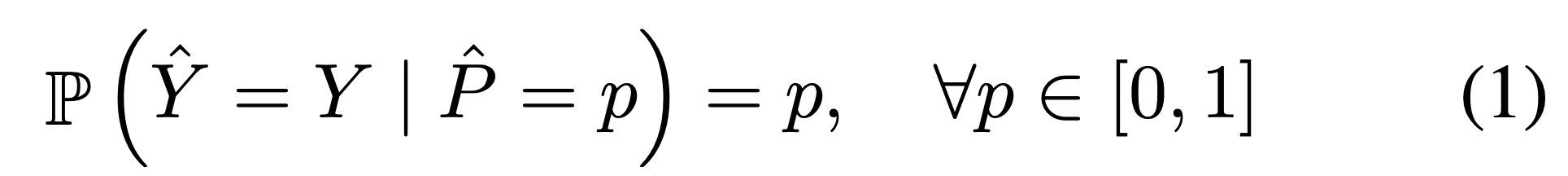
위 상태를 perfect calibration 상태라고 정의내렸다(Confidence가 p일 때, Y가 올바른 Y일 확률이 p이라는 말. 즉 Confidence 가 p일 때, Accuracy도 p다.)

Reliability Diagrams

제일 위에 그림에 아랫부분을 보면, Confidence에 대한 Accuracy의 기대 샘플값들을 나타낸다. 만약에 모델이 완벽하게 calibrated되었다면, plot은 $y=x$함수가 된다.

유한한 샘플들을 통해 기대 정확도를 측정하기 위해서, M개의 interval bins로 나누고 각각의 bin에 대한 accuracy를 구한다. $B_m$을 샘플들의 인덱스라고 했을 때, 이것들의 예측 confidence는 $I_m=({m-1\over{M}},{m\over{M}}]$에 채워진다.

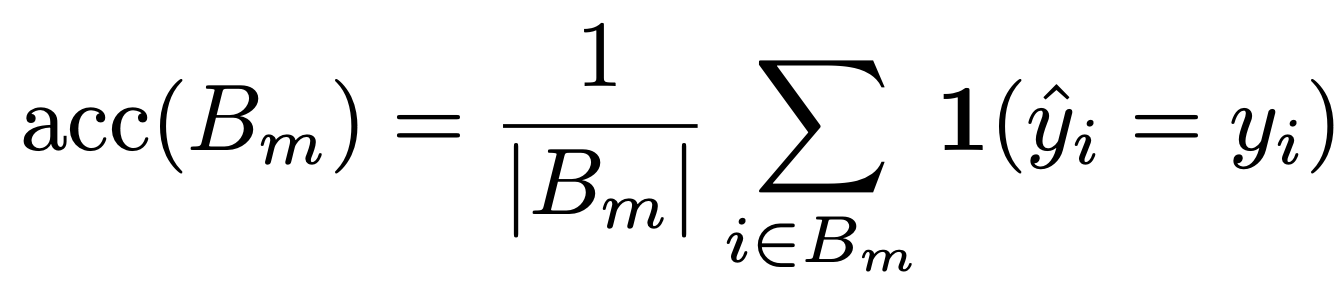
이 때 $acc(B_m)$은 단순히 $B_m$ m번째 bin에 해당하는 샘플들에 대한 정답을 맞춘 정확도 평균을 나타낸다.

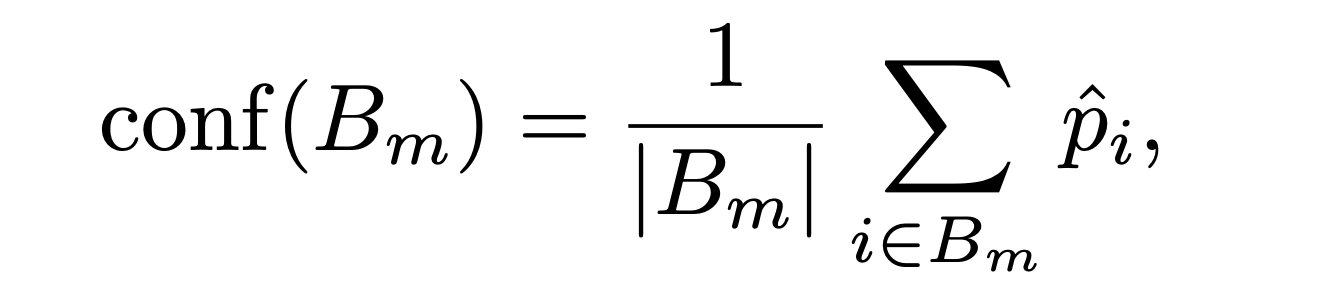
마찬가지로 $conf(B_m)$은 해당 $B_m$의 bin에 해당하는 샘플들의 Confidence값 평균을 나타낸다.

이 때, perfectly calibrated model이라고 불리는 것들은

$acc(B_m) = conf(B_m)$ for all $m\in{\{1,...,M}\}$을 가진다.

Expected Calibration Error (ECE)

위에서 설명한 Reliability Diagram은 시각적으로 표현하기 매우 유용하지만, ECE(Expected Calibration Error)는 하나의 스칼라 값으로, 모델의 칼리브레이션을 표현할 수 있다. 그런데, 두 분포를 하나의 포괄적인 의미로 표현하는 것이 어렵기 때문에, 각각의 분포에 대한 특징들을 사용하여 나타낼 수 있다.

miscalibration의 하나는 Confidence와 Accuracy의 기대값의 차이를 나타내는 것이다.

$\mathbb{E}_{\hat{P}}[|\mathbb{P}(\hat{Y}=Y|\hat{P}=p)-p|]$

ECE는 2번식을 M개의 같은 공간을 가지는 bins를 나누어 (reliability diagram과 비슷한 방법) 추정한다. 이 때, 각 bins에 해당하는 가중치를 곱해준다. (bins의 개수가 다르니)

$\mathbf{ECE} = \Sigma^M_{m=1}{|B_m|\over{n}}|acc(B_m) - conf(B_m)|$

위 식이 ECE이며, n개의 샘플을통해 acc와 conf를 bin 단위로 gap을 구한다. 가장 맨위의 Figure 1의 빨간색 바들이 바로 이 gap이다. 이 지표는 Calibration을 측정하는데 있어서 매우 중요한 metric이다.

Maximum Calibration Error (MCE)

높은 위험도를 가지고 있는 어플리케이션에서 confidence measures는 매우 중요하고, 우리는 최소한 worst-case에 해당하는 차이를 최소화 해야 한다.

$\max_{p\in[0,1]}|\mathbb{P}(\hat{Y}=Y|\hat{P}=p)-p|$

아까와 마찬가지로 모든 bins에 해당하는 값들의 최댓값을 구하면

$\mathbf{MCE}=\max_{m\in\{1,...,M\}}|acc(B_m)-conf(B_m)$

이 두가지 MCE와 ECE를 reliability diagram에 표현할 수 있다. MCE는 빨간색 바들 중에서 가장 갭이 큰 바를 의미하고, ECE는 모든 빨간색 바들의 가중평균을 의미한다.

완벽하게 칼리브레이션된 모델은 MCE와 ECE모두 0이다.

Negative log likelihood (NLL)

NLL은 확률 모델의 품질을 평가하는 표준적인 measure이다. deep learning에서는 Cross Entropy Loss로 알려져 있다. probabilistic model $\hat{\pi}(Y|X)$와 $n$샘플들이 주어졌을 때, NLL은 다음과 같다.

$\mathcal{L}=-\Sigma^n_{i=1}\log(\hat{\pi}(y_i|\mathbf{x}_i))$

---

Observing Miscalibration