Energy-based Out-of-distribution Detection
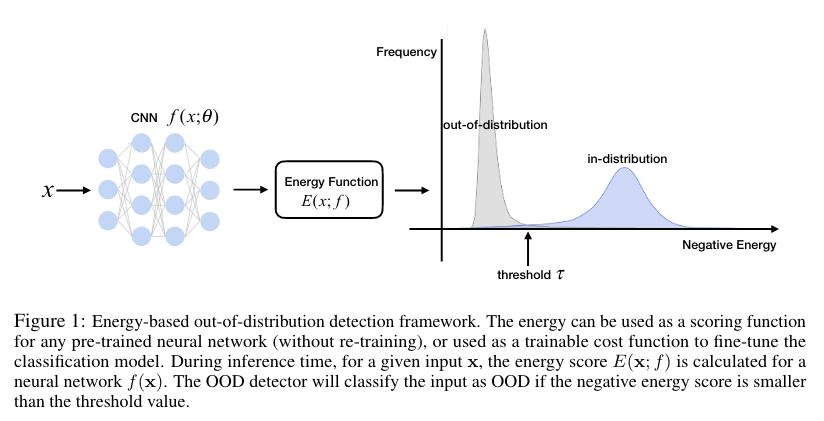
위 논문에서는 energy score를 사용한 OOD detection unified framework를 제안한다. 이러한 에너지의 차이는 in- and out-of-distribution을 효과적으로 분류할 수 있다. energy score는 softmax confidence가 가지는 OOD example에서의 arbitrarily high value가 나오게되는 치명적인 문제를 해결해준다. 먼저 pre-trained model을 통한 energy의 사용과, energy와 softmax score사이의 관계에 대해 설명한다. 그리고나서 energy를 사용한 loss를 통한 fine-tuning에 대해 설명한다.
Background : Energy-based Models
일단, 이 논문을 이해하기 위해서는 Energy-based Model에 관해 이해하고 있어야 한다. energy-based model(EBM)의 필요성은 입력 공간에 해당하는 각각의 데이터 포인트 에 대해서 어떤 energy function 을 통해 single, non-probabilistic scalr인 energy로 매핑해주는 모델링 방법이다. 이 때, energy값들의 집합은 Gibbs distribution을 통해 probability density 로 변환될 수 있는데 다음과같다.
이 때 denominator 는 partition function이라고 불리며, 에 대한 marginalize를 진행한 결과이다. 이 떄 는 temperature parameter이다. 주어진 데이터포인트 의 Helmholtz free energy에 해당하는 는 negative log partition function으로 표현할 수 있다.
Energy Function
Energy-based model은 modern machine learning과 inherent connection을 지니고 있는데, 특히 discriminative model이 그렇다. 이를 알아보기 위해서, discriminative neural classifier 라고 생각해보고, 우리는 입력 를 개의 logits으로 알고있는 real-valued number로 매핑하고자 한다. 이러한 logits은 softmax function을 이용해 categorical distribution으로 derive할 수 있다.
여기서 는 의 번째 인덱스의 로짓을 의미.
Energy based model에서의 연결을 통해서, energy를 given input 에 대한 로 정의할 수 있다.
Energy as Inference-time OOD Score
Out-of-distribution은 binary classification 문제인데, in- and out-of-distribution example 사이의 차이를 특정한 score를 통해 탐지해내는 것이다. scoring function은 in- and out-of-distribution을 구분할 수 있어야 하며, 가장 자연스러운 방법은 density function of the data 를 사용하고 낮은 likelihood를 가지는 example을 OOD로 분류해내는 것일 것이다. 그러나 이전의 연구들에서 이러한 density function을 deep generative model을 사용해 추정하는 것은 합리적인 방법이 아니라고 한다. (Do deep generative models know what they don’t know? arxiv 2018)
이러한 문제를 해결하기 위해서, 논문의 저자들은 ood detection을 위한 discriminative model로 부터의 energy function을 가져온다. negative log-likelihood (NLL)로 훈련된 모델은 in-distribution data point에 대하여 energy를 push down한다.
이를 보기 위해, negative log-likelihood loss를 살펴보면
라고 정의할 때, NLL loss는 다음과 같이 다시 쓸 수 있다.
첫번째 텀은 energy를 ground truth answer 에 대해 push down한다. 두번째 contrastive term은 Free Energy로 해석될 수 있는데, 정답이 아닌 label에 대해서 energy를 pull up한다.
간단한 유도를 통해 에 대한 energy를 다음과 같이 나타낼 수 있다.
위 논문에서는 인 에 대한 energy score를 ood score로 사용하는 방안을 채택한다.
Moreover, the energy score , is a smooth approximation of , which is dominated by the ground truth label among all labels. Therefore, the NLL loss overall pushes down the energy of in-distribution data.
