학습 정리

---

데이터의 종류

• 범주형 데이터
  • 명확한 그룹으로 구분됨.
• 수치형 데이터
  • 수로 나타난다.

범주형 데이터

• 명확한 그룹 등으로 구분되는 것을 범주형 데이터라고 한다.
• 세부적
  • 순서형 데이터
    • 각 값이 우위 등의 순서가 존재하는 데이터
    • 리커트 척도, 영화 별점표 등
  • 명목형 데이터
    • 순서가 상관없이 항목으로 구분되는 데이터, 일반적으로 값이 텍스트이다.
    • 성별, 국가, 과일 종류 등
• 데이터 분석에 있어서 집단 간 분석에 용이하다.
  • 분류 기준을 통해 범주 별 통계 지표 확인
    • 국가별 평균 임금, 지하철노선별 사용자 연령층 분포, 식료품별 가격 증감
  • 범주 별 관계 분석에도 용이하다. (추천 알고리즘)
    • 성별에 따른 구매품목 통계 비교, 영화 카테고리 추천
• 이러한 데이터의 집단에서 추출할 수 있는 대표 값 종류
  • 평균 / 총합
  • 기댓값(가중평균)
  • 최빈값
  • 중앙값
  • 사분위값
  • 절사평균

---

명목형 데이터

• 순서가 상관없이 항목으로 구분되는 데이터, 일반적으로 값이 텍스트이다.
• 성별, 국가, 과일 종류 등
• ML/AI 모델에 넣기 위해서는 수 또는 수 배열로 치환하는 과정이 필요하다. (일부 Decision Tree와 Boosting Model 제외)
  • 명목형 데이터 처리 방법 종류
    • Label Encoding
      • 가장 쉬운 1대 1 매핑 ex) 여자, 남자 -> 0, 1
      • 없는 레이블에 대해서 미리 전처리가 필요하다. (기본값 -1)
      • [0, 1, 2, 3]등 자체적인 순서가 존재한다.
    • One Hot Encoding
      • 순서 정보를 없애기 위해서 해당 하는 col만 1로 만든다.
      • [사과, 배, 과일] -> [1, 0, 0], [0, 1, 0], [0, 0, 1]
      • 변수에 따라서 데이터가 매우 커질 수 있다.
      • 학습 속도와 퀄리티에 지장을 줄 수 있다.
    • Binary Encoding
      • 2진수를 활용한 방식
      • 0, 1, 2, 3 이런식으로 레이블링을 진행
      • 이를 이진수로 변환 -> 00, 01, 10, 11
      • 변환한 이진수로 컬럼 데이터로 변환 -> [0, 0], [0, 1], [1, 0], [1, 1]
      • 순서 정보를 없애며, 개수가 많은 범주에 대해서 효과적이다.
      • 하지만 범주의 의미가 거의 사라져 버린다.
    • Enbedding
    • Hashing

---

순서형 데이터

• 각 값이 우위 등의 순서가 존재하는 데이터
• 리커트 척도, 영화 별점표 등
• 명목형 데이터에 순서 정보가 추가된 것이다.
• 명목형에서 사용가능한 인코디 방법은 모두 사용 가능하다.

---

순환형 데이터

• 순서는 있지만 해당 값이 순환하는 경우 (범주형 / 수치형 모두 포함된다)
• 월(1월 ~ 12월), 요일 (월 ~ 일), 각도(0도 ~ 360도)
• 삼각함수 등 값의 크기에 따라 순환되는 값을 사용할 수 있다.

---

수치형 데이터

• 분류
  • 일반적인 정수 형태를 띄고 있는 이산형 데이터(Discrete)
    • 인구 수, 제품 수, 횟수 등
  • 실수 형태를 띄고 있는 연속형 데이터(Continuous)
    • 키, 몸무게, 온도 등
• 대표값을 추출하여 진행하는 것은 잘못된 정보를 제공할 수 있다.
  • 평균과 분산이 같음에도 데이터의 분포가 전부 다른 유명한 예시가 존재한다.
• 그렇기 때문에 데이터가 가지고 있는 여러 정보의 형태를 확인하여 필요한 정보를 추출 할 수 있어야한다. (시각화의 필요성)

---

수치형 데이터의 전처리

모델의 입력 값으로 넣는 것은 간단하지만 모델에 따라 범위에 대한 문제가 존재한다.
이는 알고리즘의 정확도와 속도에도 영향을 미치므로 분석에 있어서 같은 범주로 비교해야 한다.

• 정규화
  • 데이터의 범위를 [0, 1] 또는 [-1, 1]과 같은 특정 범위로 변환
  • $\frac{x - min}{max - min}$
• 표준화
  • 데이터의 평균을 0, 표준편차를 1로 만들어, 데이터를 표준 정규 분포 형태로 변환한다.
  • $\frac{x - mean}{std}$
• 치우친 데이터 처리 방법
  
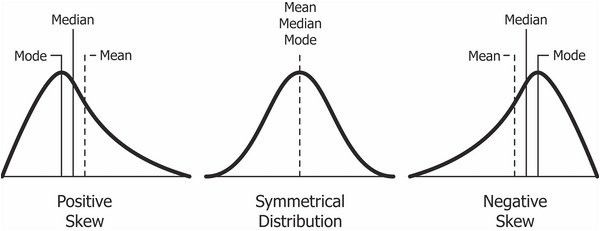
  • positive Skew는 작은 값에 값들이 모여있다.
    • 작은 값의 구간을 큰 값보다 더 효과적으로 크게 만든다.
    • 로그 변환 (0 이상 실수라는 조건)
    • 제곱근 (양수라는 조건)
  • negative Skew는 칸 값에 값들이 모여있다.
    • 큰 값의 구간을 작은 값보다 더 효과적으로 작게 만든다.
    • 큰 값이 서로 더 차이가 크게해서 분포를 넓힌다.
    • 제곱 변환 또는 거듭제곱, 지수함수를 이용한다.