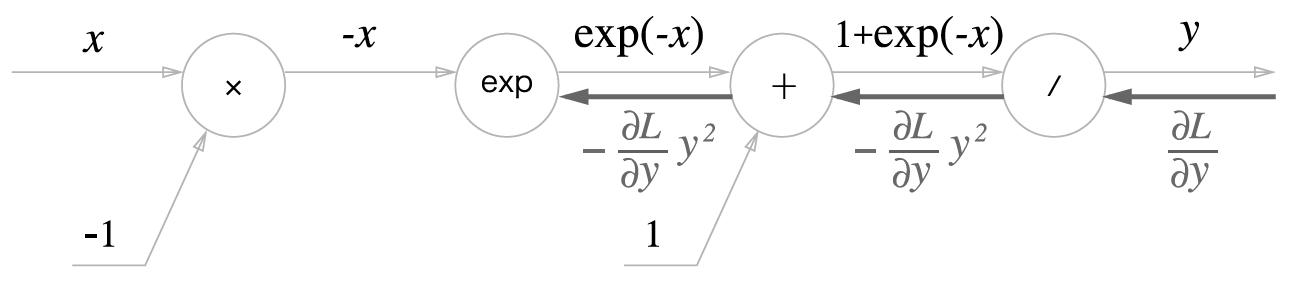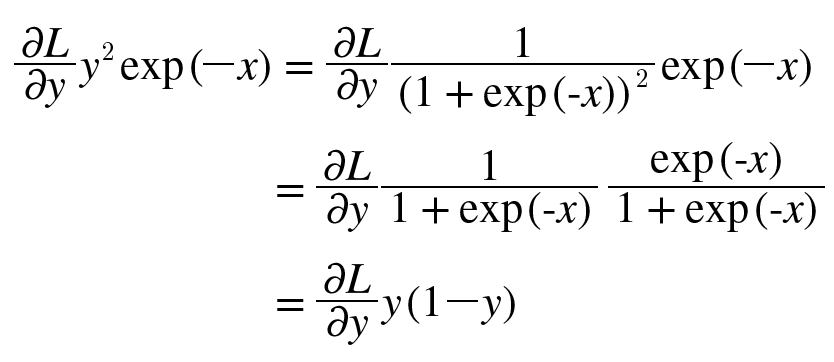[밑바닥부터 시작하는 딥러닝] CHAPTER 5. 오차역전파법

Lil Park·2021년 7월 27일
1

5.5 활성화 함수 계층 구현하기

5.5.1 ReLU 계층

5.5.2 Sigmoid 계층

  • Sigmoid 함수
h(x)=11+exp(−x)h(x) = \dfrac{1}{1 + exp(-x)}
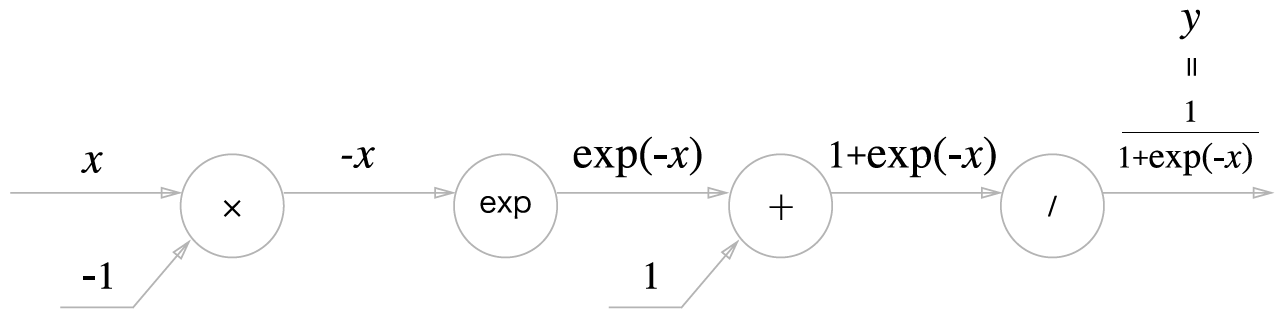
  • Sigmoid 함수의 계산 그래프 (forward pass)

  • Sigmoid 함수 역전파
    1. '/' 노드, 즉 y=1xy=\dfrac{1}{x}을 미분
      ∂y∂x=−1x2=−y2\cfrac{\partial y}{\partial x} = -\dfrac{1}{x^2} = -y^2
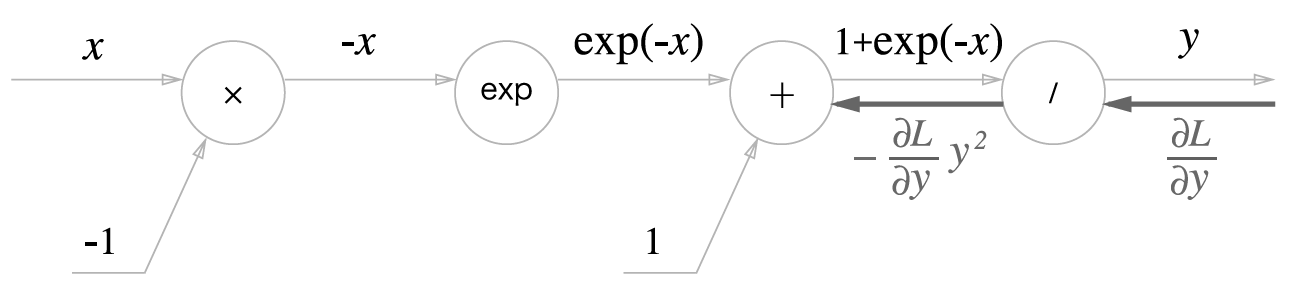
    2. '+' 노드는 상류의 값을 여과 없이 하류로 보냄
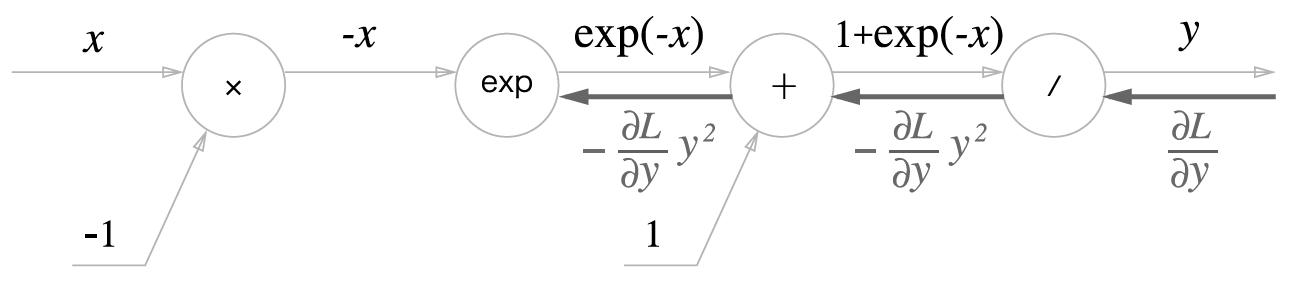
    3. 'exp' 노드는 y=exp(x)y=exp(x) 연산을 수행
      ∂y∂x=exp(x)\cfrac{\partial y}{\partial x} = exp(x)
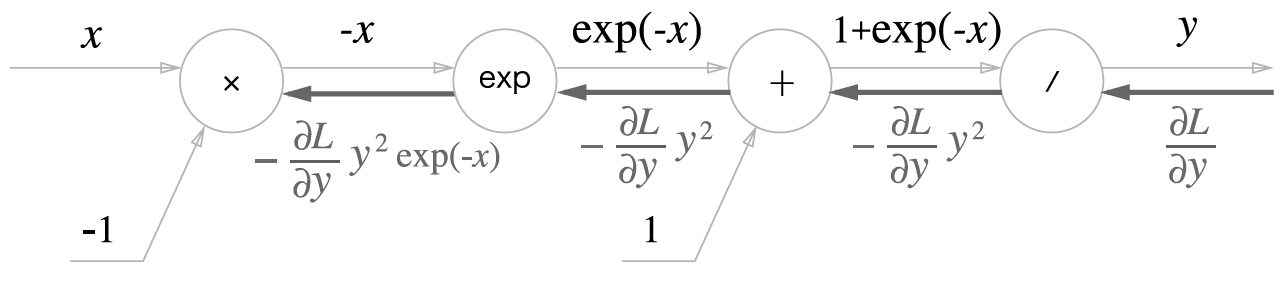
    4. 'x' 노드는 순전파 때의 값을 서로 바꿔 곱함
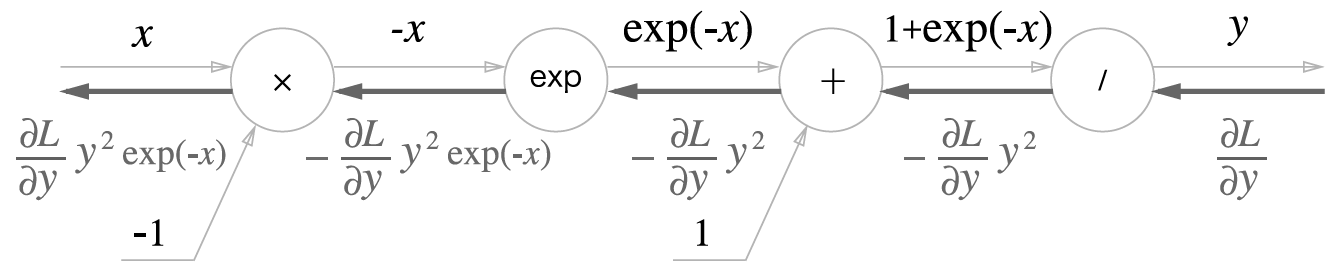
  • 위의 과정을 모두 묶어, 다음 이미지와 같이 단순한 'sigmoid' 노드 하나로 대체 가능

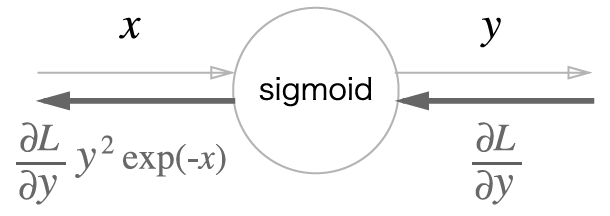
  • 또한, ∂L∂yy2exp(−x)\cfrac{\partial L}{\partial y}y^2exp(-x)는 다음과 같이 정리 가능

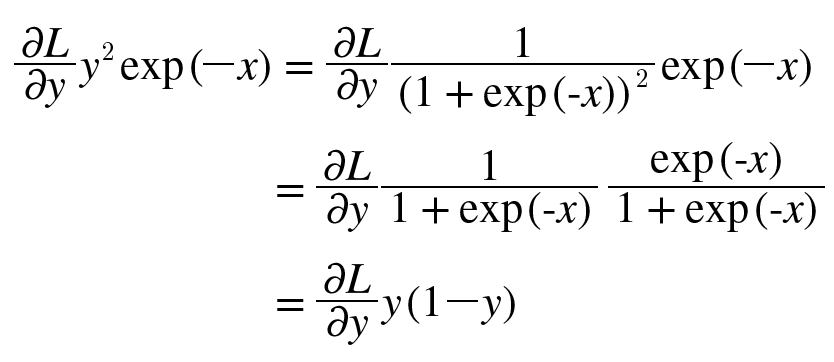
  • sigmoid 계층의 역전파는 순전파의 출력(yy)만으로 계산 가능
class Sigmoid:
    def __init__(self):
        self.out = None
    
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        
        return dx

5.6 Affine/Softmax 계층 구현하기

5.6.1 Affine 계층

  • 신경망의 순전파에서는 가중치 신호의 총합을 계산하기 때문에, 행렬의 내적(np.dot())을 사용
  • 신경망의 순전파 때 수행하는 행렬의 내적은 기하학에서는 어파인 변환(affine transformation)
X = np.random.rand(2)     # 입력
W = np.random.rand(2, 3)  # 가중치
B = np.random.rand(3)     # 편향

X.shape  # (2,)
W.shape  # (2, 3)
B.shape  # (3,)

Y = np.dot(X, W) + B
  • 해당 코드를 계산 그래프로 나타내면 다음과 같음

  • 해당 그래프의 역전파

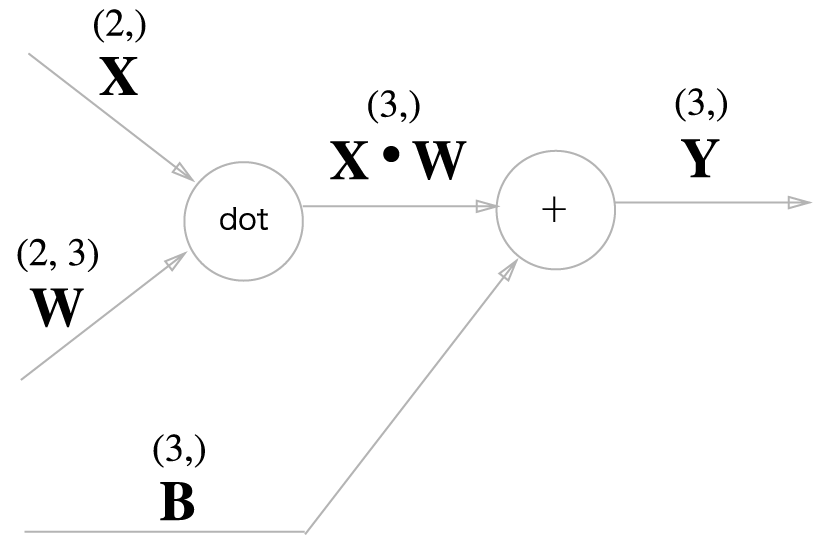
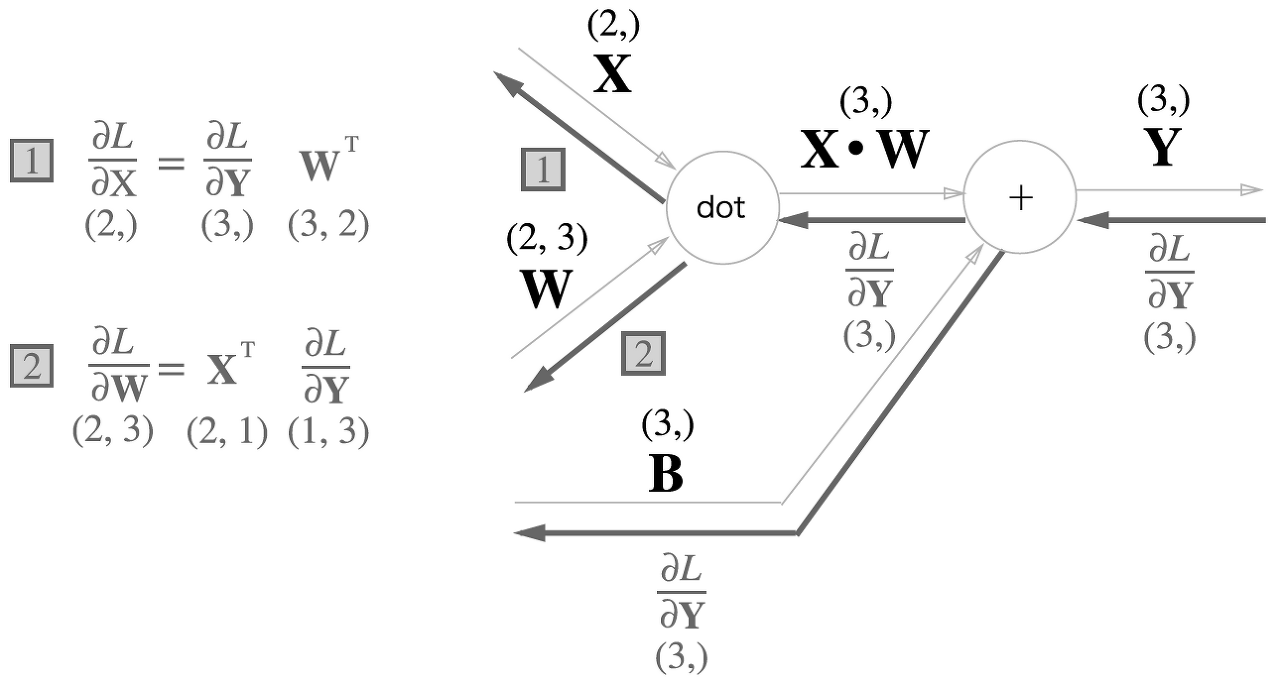
5.6.2 배치용 Affine 계층

  • 지금까지의 Affine 계층은 입력 데이터로 X 하나만을 고려했음
  • 데이터 N개를 묶어 순전파하는 경우, 즉 배치용 Affine 계층을 고려

  • 순전파의 편향 덧셈은 각각의 데이터에 더해짐
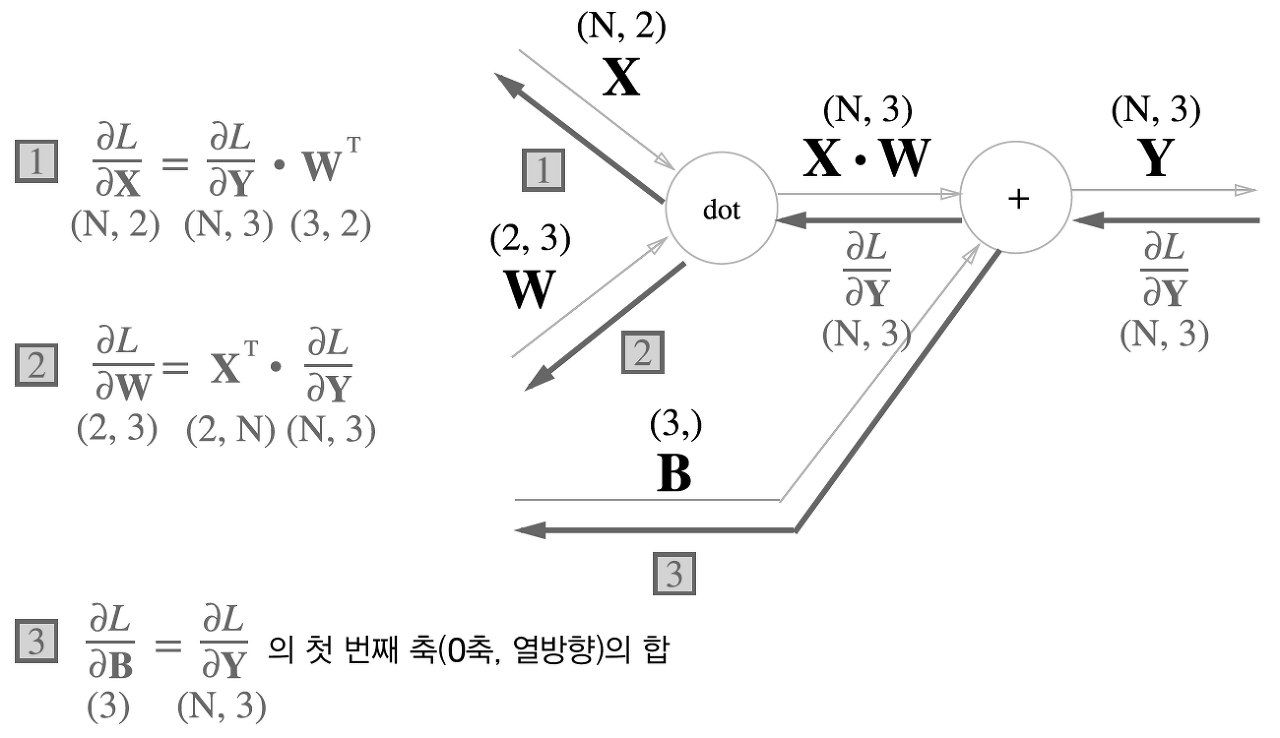
X_dot_W = np.array([[0, 0, 0], [10, 10, 10]])
B = np.array([1, 2, 3])

X_dot_W + B   # [[1, 2, 3], [11, 12, 13]]
  • 따라서, 역전파 때는 각 데이터의 역전파 값이 편향의 원소에 모여야 함
dY = np.array([[1, 2, 3], [4, 5, 6]])

dB = np.sum(dY, axis=0)   # dB = [5, 7, 9]
  • Affine 구현
class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
        
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        
        return out
        
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        return dx

5.6.3 Softmax-with-Loss 계층

  • 출력층에서 사용하는 Softmax 함수
  • Softmax 함수는 입력 값을 정규화하여 출력
  • Softmax 계층을 구현하는데, 손실 함수인 교차 엔트로피 오차(cross entropy error)도 포함하여 'Softmax-with-Loss 계층'이라는 이름으로 구현

  • 위의 계산 그래프를 다음과 같이 간소화

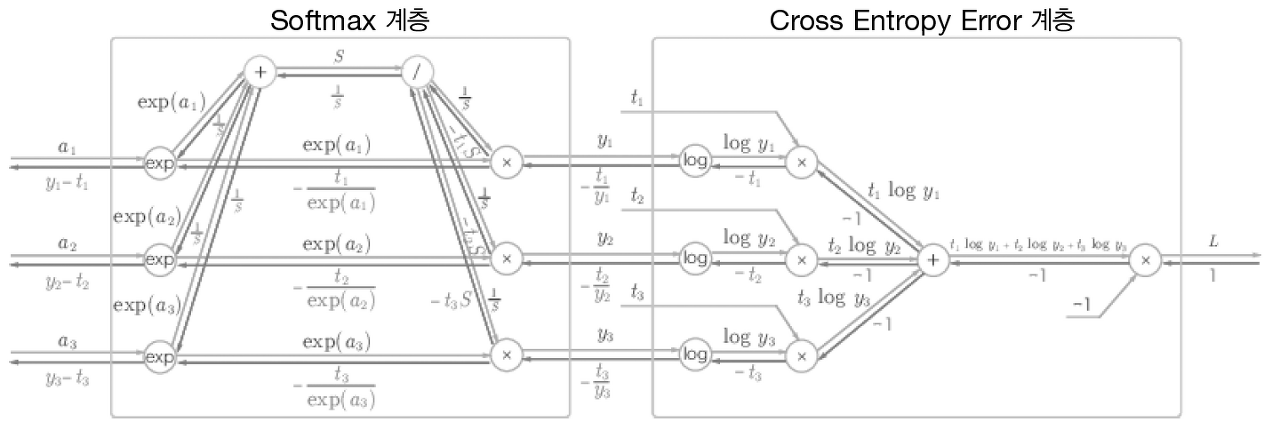
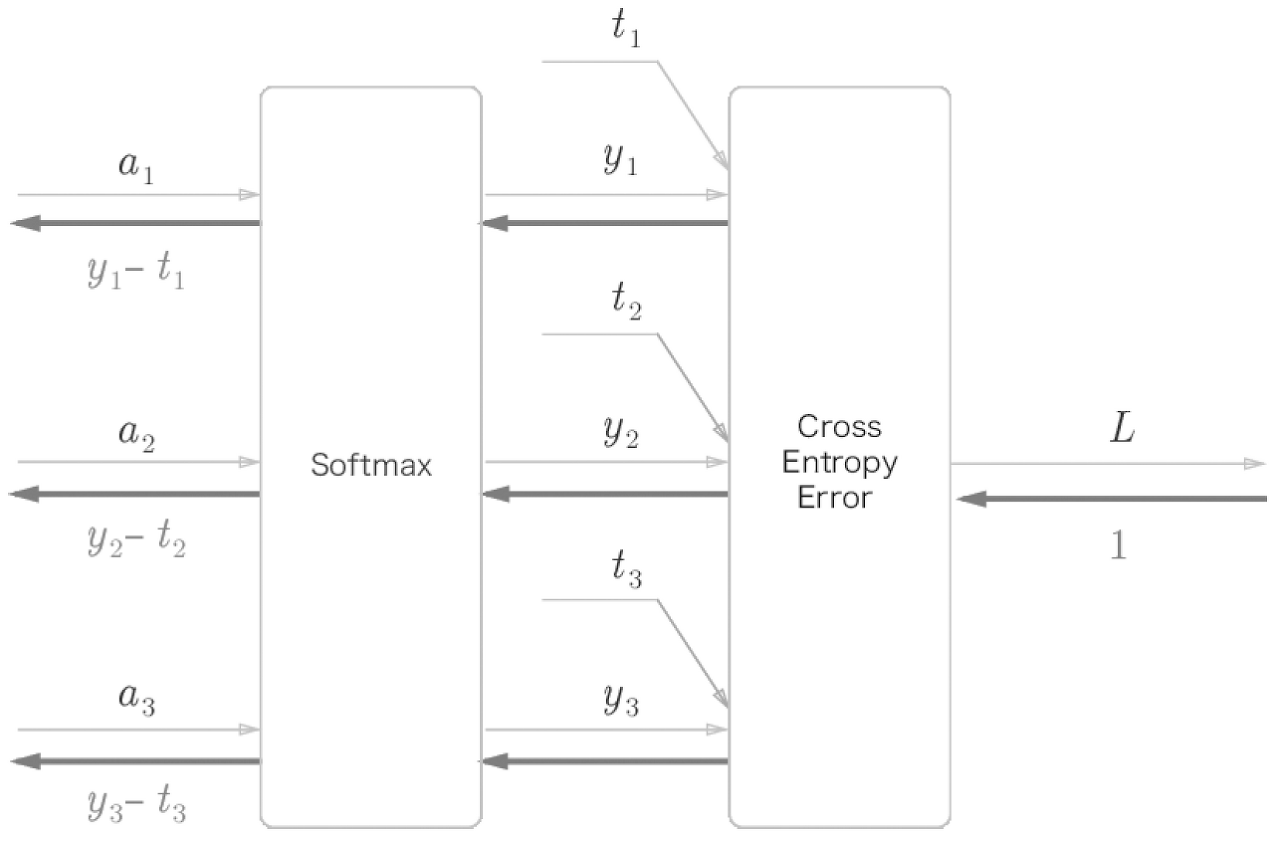
  • Softmax 계층의 역전파는 (y1−t1,y2−t2,y3−t3)(y_1 - t_1, y_2 - t_2, y_3 - t_3)라는 말끔한 결과를 도출
  • 결국, 신경망의 역전파에서는 오차(출력과 정답 레이블의 차이)가 앞 계층에 전달
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None  # 손실
        self.y = None     # softmax의 출력
        self.t = None     # 정답 레이블
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss
        
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx

5.7 오차역전파법 구현하기

5.7.1 신경망 학습의 전체 그림

  • 전체
    • 신경망에는 적응 가능한 가중치와 편향이 존재
    • 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정 (학습)
    • 학습은 다음과 같이 4단계로 수행
  • 1단계 - 미니배치
    • 훈련 데이터 중 일부를 무작위로 선택
    • 이렇게 선별한 데이터를 미니배치라 하며, 미니배치의 손실 함수 값을 줄이는 것이 목표
  • 2단계 - 기울기 산출
    • 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 계산
    • 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시
  • 3단계 - 매개변수 갱신
    • 가중치 매개변수를 기울기 방향으로 아주 조금 갱신
  • 4단계 - 반복
    • 1~3단계를 반복

5.7.2 오차역전파법을 적용한 신경망 구현하기

  • 2층 신경망을 TwoLayerNet 클래스로 구현

# coding: utf-8
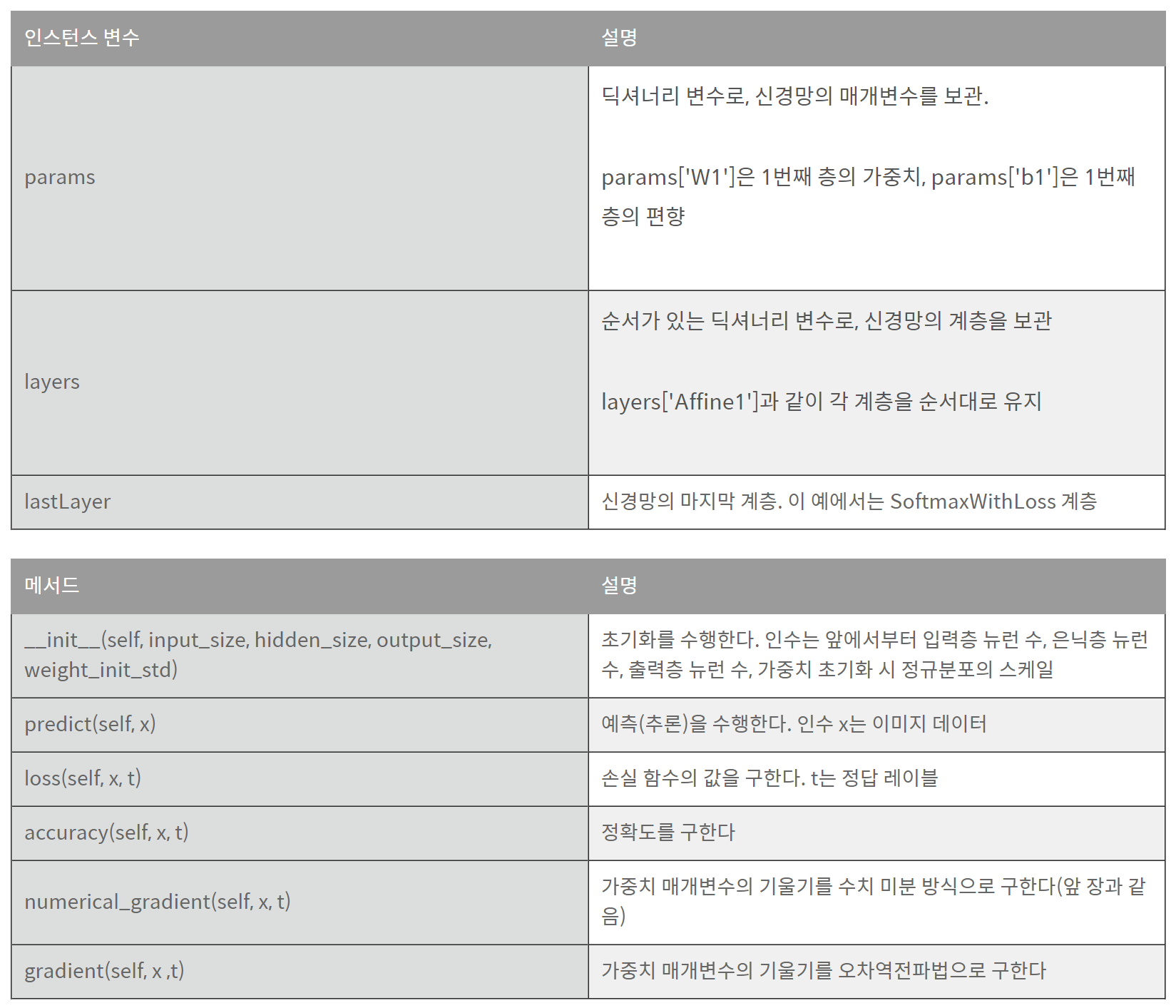
import sys, os
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
        
    # x : 입력 데이터, t : 정답 레이블
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x : 입력 데이터, t : 정답 레이블
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 결과 저장
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

5.7.3 오차역전파법으로 구한 기울기 검증하기

  • 오차역전파법은 매개변수가 많아도 효율적으로 계산 가능
  • 수치 미분을 이용하는 방법은 느리지만, 오차역전파법을 정확히 구현했는지 확인하기 위해 필요
  • 두 방식으로 구한 기울기가 일치함을 확인하는 작업을 기울기 확인(gradient check)
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

# 각 가중치의 절대 오차의 평균을 구한다.
for key in grad_numerical.keys():
    diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
    print(key + ":" + str(diff))
  • 각 가중치 매개변수 차이의 절댓값을 구하고, 이를 평균한 값이 오차
  • 이를 통해서 수치 미분과 오차역전파법으로 구한 기울기의 차이를 구하고, 오차역전파법으로 구한 기울기의 신뢰도를 높임

5.7.4 오차역전파법을 사용한 학습 구현하기

  • 마지막으로 오차역전파법을 사용한 신경망 학습을 구현
# coding: utf-8
import sys, os
sys.path.append(os.pardir)

import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 기울기 계산
    #grad = network.numerical_gradient(x_batch, t_batch) # 수치 미분 방식
    grad = network.gradient(x_batch, t_batch) # 오차역전파법 방식(훨씬 빠르다)
    
    # 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

5.8 정리

  • 계산 그래프를 이용하면 계산 과정을 시각적으로 파악할 수 있다.
  • 계산 그래프의 노드는 국소적 계산으로 구성된다. 국소적 계산을 조합해 전체 계산을 구성한다.
  • 계산 그래프의 순전파는 통상의 계산을 수행한다. 한편, 계산 그래프의 역전파로는 각 노드의 미분을 구할 수 있다.
  • 신경망의 구성 요소를 계층으로 구현하여 기울기를 효율적으로 계산할 수 있다. (오차역전파법)
  • 수치 미분과 오차역전파법의 결과를 비교하면 오차역전파법의 구현에 잘못이 없는지 확인할 수 있다. (기울기 확인)
profile
Lil Park
코딩하는 물리학도
이전 포스트

[밑바닥부터 시작하는 딥러닝] CHAPTER 3. 신경망

다음 포스트

[밑바닥부터 시작하는 딥러닝] CHAPTER 5. 오차역전파법

0개의 댓글