[CS231n] Lecture 7: Training Neural Networks II 정리

• 이번 lecture에서는 다음의 내용을 다룰 예정
  • Fancier optimization
  • Regularization
  • Transfer Learning

• Neural Network에서 가장 중요한 것은 바로 최적화 문제
  • Network의 가중치에 대해서 손실 함수를 정의해 놓으면, 손실 함수는 가중치가 얼마나 좋은지 나쁜지를 알려줌
  • 손실 함수는 가중치가 모여 있는 산
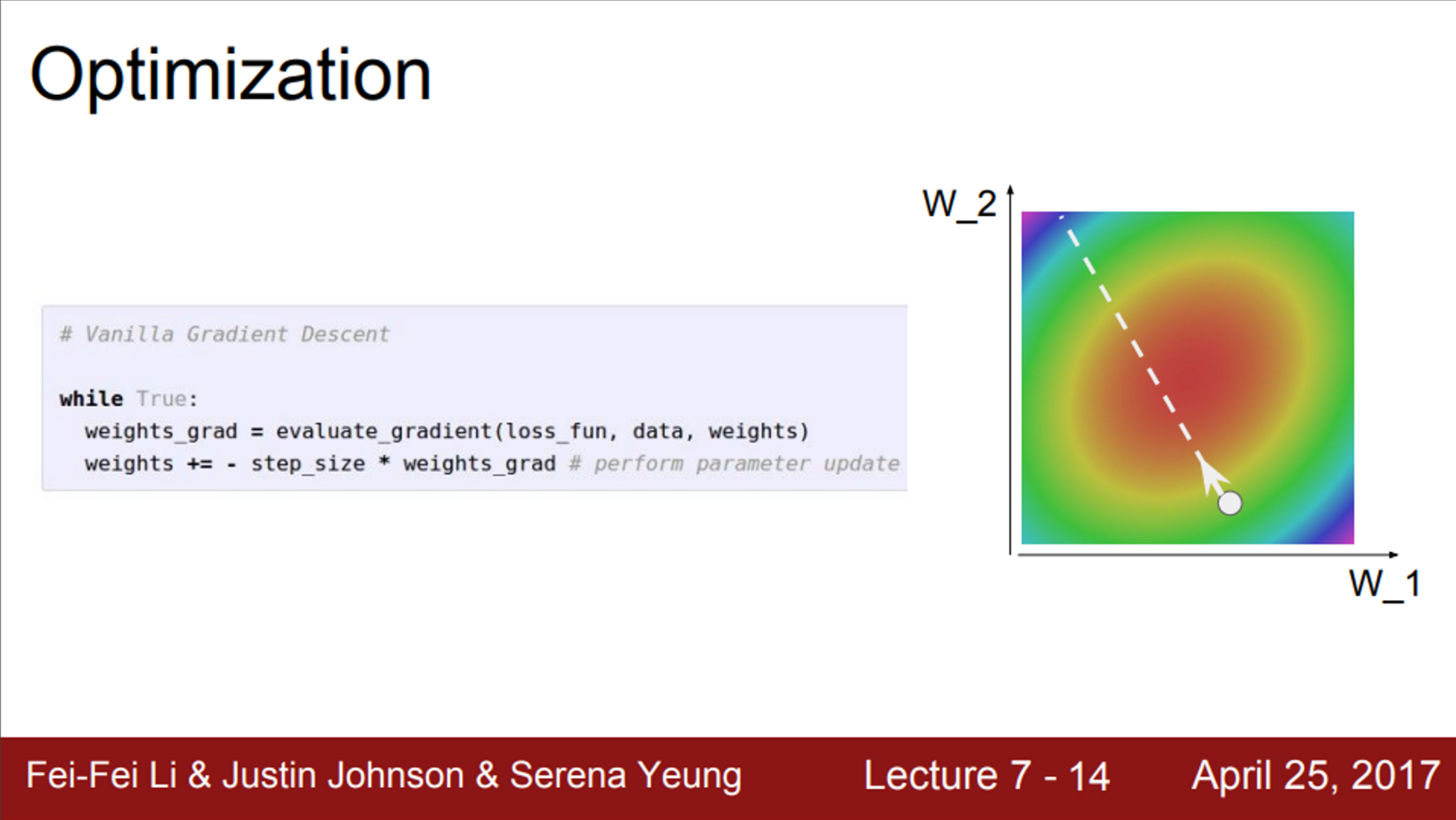
    • 오른쪽 그림의 예시는, 가중치를 표현한 예시
    • $W_1$, $W_2$를 최적화 시키는 문제
    • 우리의 목적은, 가장 붉은색 지점을 찾는 것 (가장 낮은 Loss를 가진 가중치)
  • 가장 간단한 최적화 알고리즘은 Stochastic Gradient Descent(SGD)
    • 우선, 미니 배치 안의 데이터에서 Loss를 계산
    • 그 후, Gradient의 반대 방향을 이용해서 파라미터를 업데이트
    • 이 과정을 반복하면, 결국 붉은색 지점으로 수렴할 것이고, Loss가 가장 낮은 곳에 도달
  • 그러나, 이 심플한 알고리즘을 사용하게 되면 몇 가지 문제에 봉착함

• 가령, 손실 함수가 위와 같이 생겼고, $W_1$, $W_2$가 있다고 가정해보면,
  • 둘 중 하나는 업데이트를 해도, 손실 함수가 아주 느리게 변함
    • 즉, 수평 축의 가중치는 변해도 Loss가 아주 천천히 줄어듦
    • Loss는 수직 방향의 가중치 변화에 훨씬 더 민감하게 반응
    • 다시 말하면, 현재 지점에서 Loss는 bad condition number를 지니고 있다고 말할 수 있음
    • 해당 지점의 Hessian matrix의 최대/최소 sigular value 값의 비율이 매우 안좋다는 뜻
  • 이런 환경에서 SGD를 수행하면, 위와 같은 특이한 지그재그 형태를 볼 수 있음
    • 함수에서 gradient의 방향이 고르지 못하기 때문에
    • gradient를 계산하고 업데이트 하게 되면, line을 넘나들면서 왔다갔다 하게 됨
    • Loss에 영향을 덜 주는 수평 방향 차원의 가중치는 업데이트가 아주 느리게 진행됨
    • 좋지 않은 현상이며, 이러한 문제는 고차원 공간에서 훨씬 더 빈번하게 발생함

• SGD에서 발생하는 또 다른 문제는 local minima와 saddle points와 관련된 문제
  • x축은 하나의 가중치를 뜻하고, y축은 loss를 뜻한다고 할 때,
  • 손실 함수 중간에 valley가 하나 있음
    • 이런 경우, SGD는 멈춰버림
    • 해당 valley에서 gradient가 0이 되기 때문에 (locally flat)
    • SGD의 동작을 생각해보면, gradient를 계산하고, 그 반대 방향으로 이동하는 것
    • 위 그래프의 valley에서 gradient는 0이 되고, 따라서 opposite gradient도 0이 되기 때문에, 학습이 멈춤

• local minima는 아니지만, 한쪽 방향으로 증가하고 있고, 다른 한쪽 방향으로는 감소하고 있는 지역을 생각해볼 수 있음
  • saddle point에서도 gradient = 0 이므로, 멈춰버림
• Deep Neural Network가 local minima보다 saddle point에 더 취약함
• 또한, saddle point 뿐만 아니라, saddle point 근처에서도 문제가 발생
  • 예시를 보면, saddle point 근처에서 gradient가 0은 아니지만, 기울기가 매우 작음
    • 이것이 의미하는 바는, gradient를 계산해서 업데이트를 해도, 기울기가 매우 작기 때문에, 현재 가중치의 위치가 saddle point 근처라면 업데이트는 아주 느리게 진행

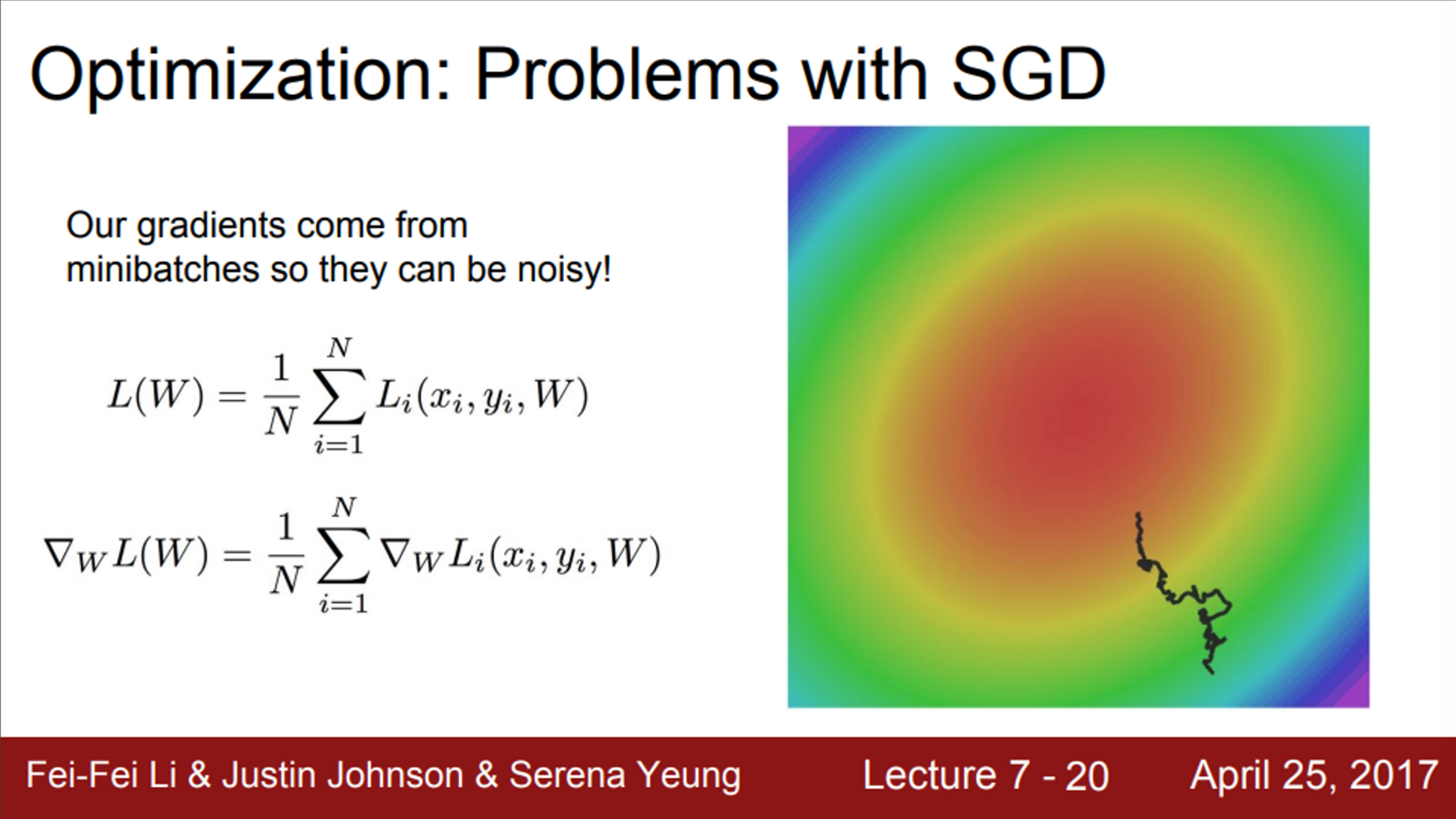
• SGD의 또 다른 문제는,
  • 손실 함수를 계산할 때, 엄청 많은 training set 각각의 loss를 전부 계산해야함
    • 그래서 실제로는, 미니 배치의 데이터들만 가지고, 실제 Loss를 추정하기만 함
    • 이는 매번 정확한 gradient를 얻을 수 없다는 것을 의미
    • gradient의 부정확한 추정값(noisy estimate)만을 구할 뿐

• 앞서 언급한 SGD의 문제들을 해결하기 위해서, momentum을 추가함
  • 왼쪽의 classic SGD를 보면, 오로지 gradient 방향으로만 움직임
  • 반면, 오른쪽 SGD + momentum을 보면, 기존 SGD에서 조금의 변화만 존재
    • 아이디어는, velocity를 유지하는 것
    • gradient를 계산할 때, velocity를 이용
    • 현재 미니 배치의 gradient 방향만 고려하는 것이 아니라, velocity를 같이 고려하는 것 (velocity에 gradient를 더해주는 방식)
    • 따라서, gradient vector의 방향이 아닌, velocity vector의 방향으로 나아감

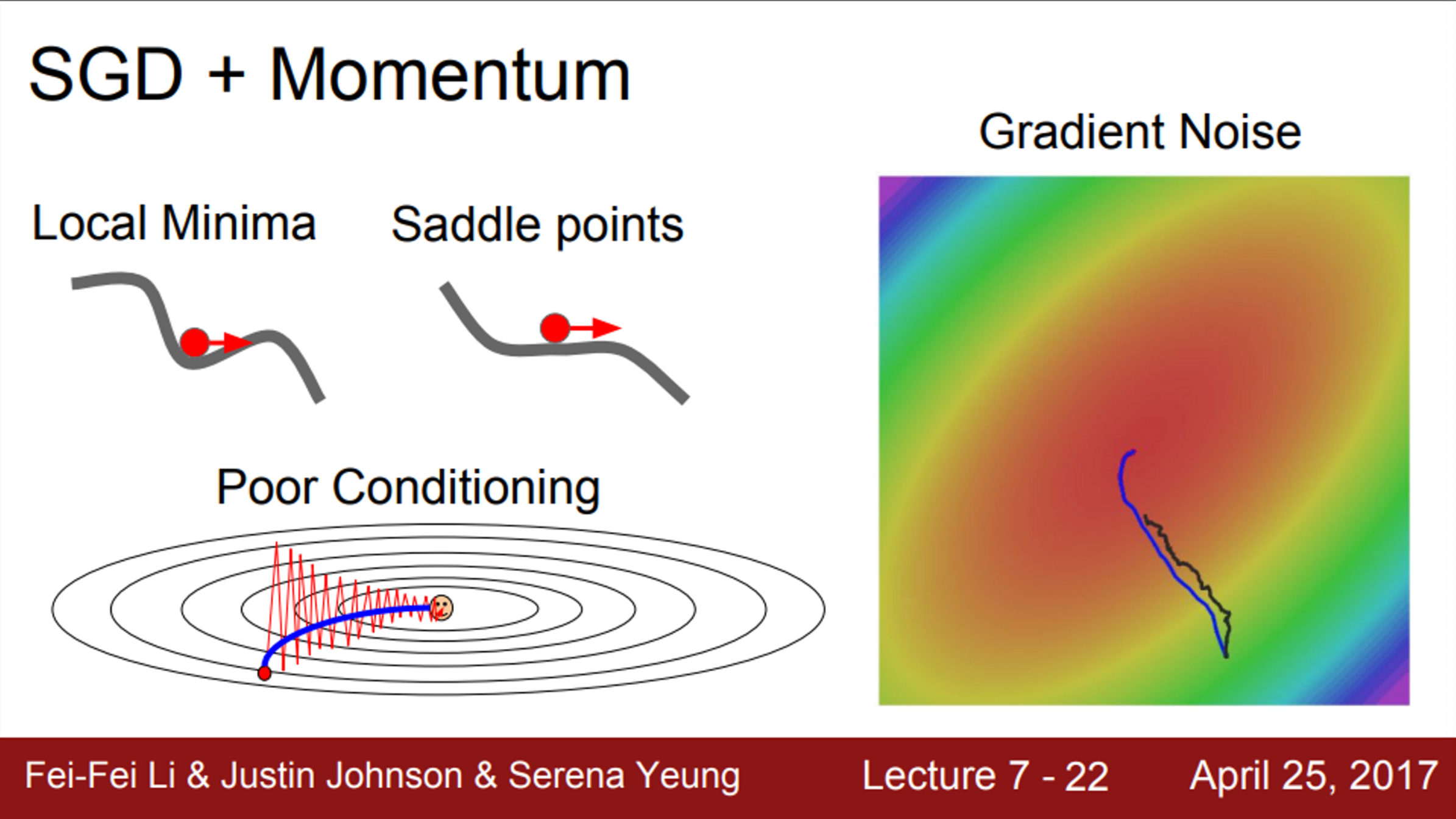
• 이러한 방법을 통해서, SGD의 문제점을 해결
  • local minima와 saddle point 문제에서,
    • local minima에 도달해도, 여전히 velocity를 가지고 있기 때문에, gradient=0 이라도 움직일 수 있음 (공을 굴렸을 때의 모습)
    • 따라서, local minima를 극복할 수 있음 (saddle point도 마찬가지)
  • 업데이트가 잘 안되는 문제에서, (poor conditioning)
    • 그림과 같이 지그재그로 움직이는 상황이라면, momentum이 이 변동을 상쇄시킴
    • 이를 통해서, loss에 민감한 수직 방향의 변동은 줄여주고, 수평 방향의 움직임은 점차 가속화 될 것
    • 즉, momentum을 추가하게 되면, high condition number problem을 해결하는데 도움이 됨

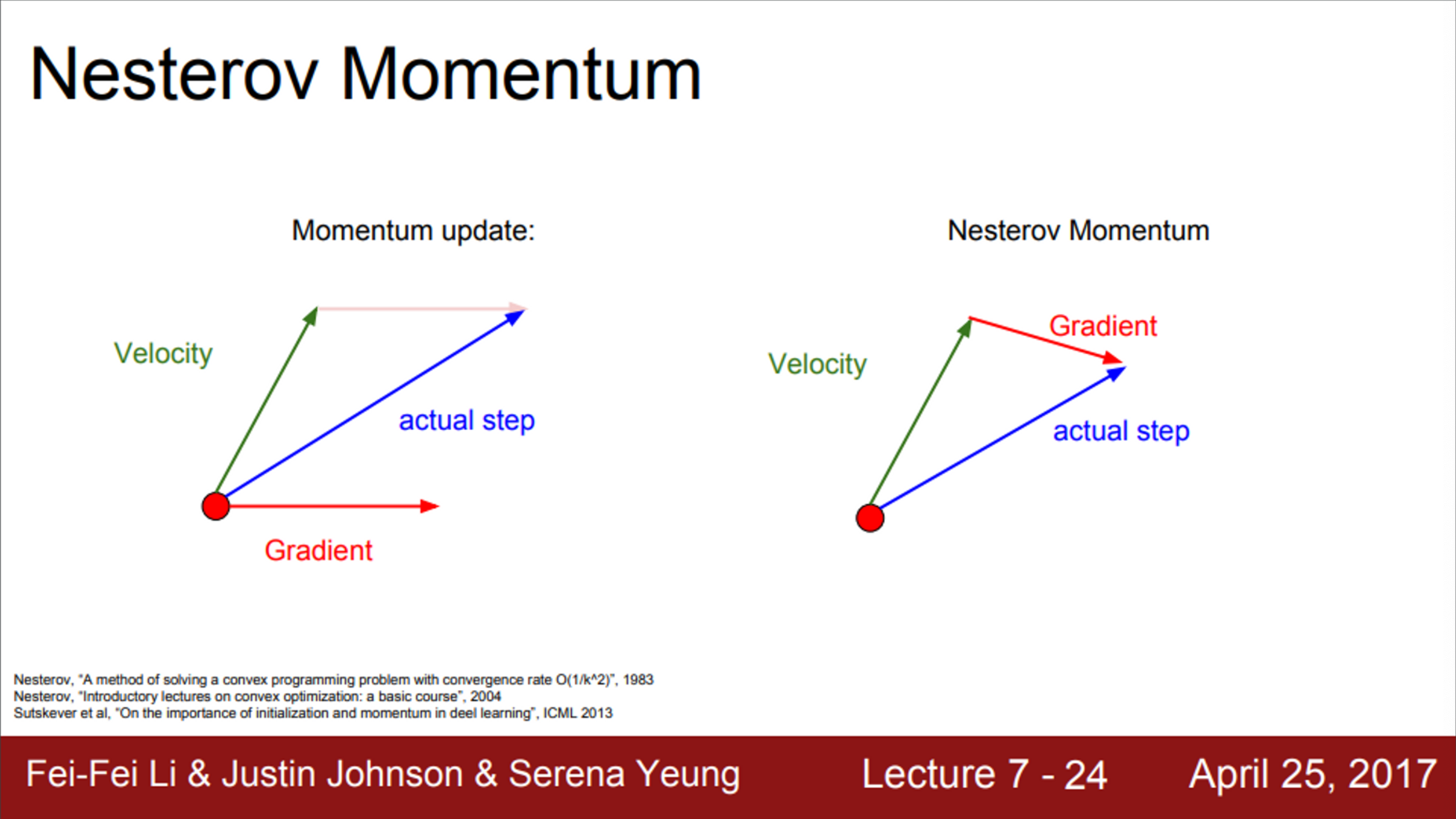
• SGD momentum을 연상할 때, 유용한 그림
  • 빨간 점이 현재 위치, 빨간색 vector는 gradient의 방향, 초록색 vector는 velocity의 방향일 때,
    • 실제 업데이트는 빨간색 vector와 초록색 vector의 가중 평균으로 구할 수 있음
    • 이는 gradient의 noise를 극복할 수 있게 해줌
  • Nesterov momentum은 SGD momentum의 변형
    • 계산하는 순서만 살짝 변형
    • SGD momentum은 현재 지점에서의 gardient를 계산한 뒤에 velocity와 섞어 줌
    • Nesterov는 빨간 점에서 velocity 방향으로 이동한 후, 그 지점에서 gradient를 계산
    • 그 후, 다시 원점으로 돌아가서 velocity와 gradient를 합침
    • Nesterov는, 만약, velocity의 방향이 잘못되었을 경우, 현재 gradient 방향을 좀 더 활용할 수 있도록 해줌
    • Nesterov는 Convex optimization 문제에서는 뛰어난 성능을 보이지만, Neural Network와 같은 non-convex problem에서는 성능이 보장되지 않음

• Nesterov의 수식
  • velocity를 업데이트하기 위해,
    • 이전의 velocity ($v_t$) 와 $(x_t+\rho v_t$) 에서의 gradient를 계산
    • 이 후, step update는 앞서 계산한 velocity ($v_{t+1}$)를 이용해서 구함
• 기존에는 Loss와 gradient를 같은 점($x_t$)에서 구했으나, Nesterov는 다른 점에서 구함
  • 즉, 미리 가 본 위치에서 gradient를 계산한 후, 다시 돌아와야 하기 때문에 복잡함
  • 변수들을 적절히 잘 바꿔주면, Nesterov를 조금 다르게 표현할 수 있으며, Loss와 gradient를 같은 점에서 계산할 수 있음
    • 첫 번째 수식은, 기존의 momentum과 동일함
    • 기존과 동일하게, velocity와 계산한 gradient를 일정 비율로 섞어주는 역할
    • 두 번째 수식을 보면, 현재 점과 velocity를 더해준 후, (현재 velocity - 이전 velocity)를 계산해서 일정 비율을 곱하고 더해줌
    • 즉, 현재/이전 velocity간의 에러 보정이 추가되었음

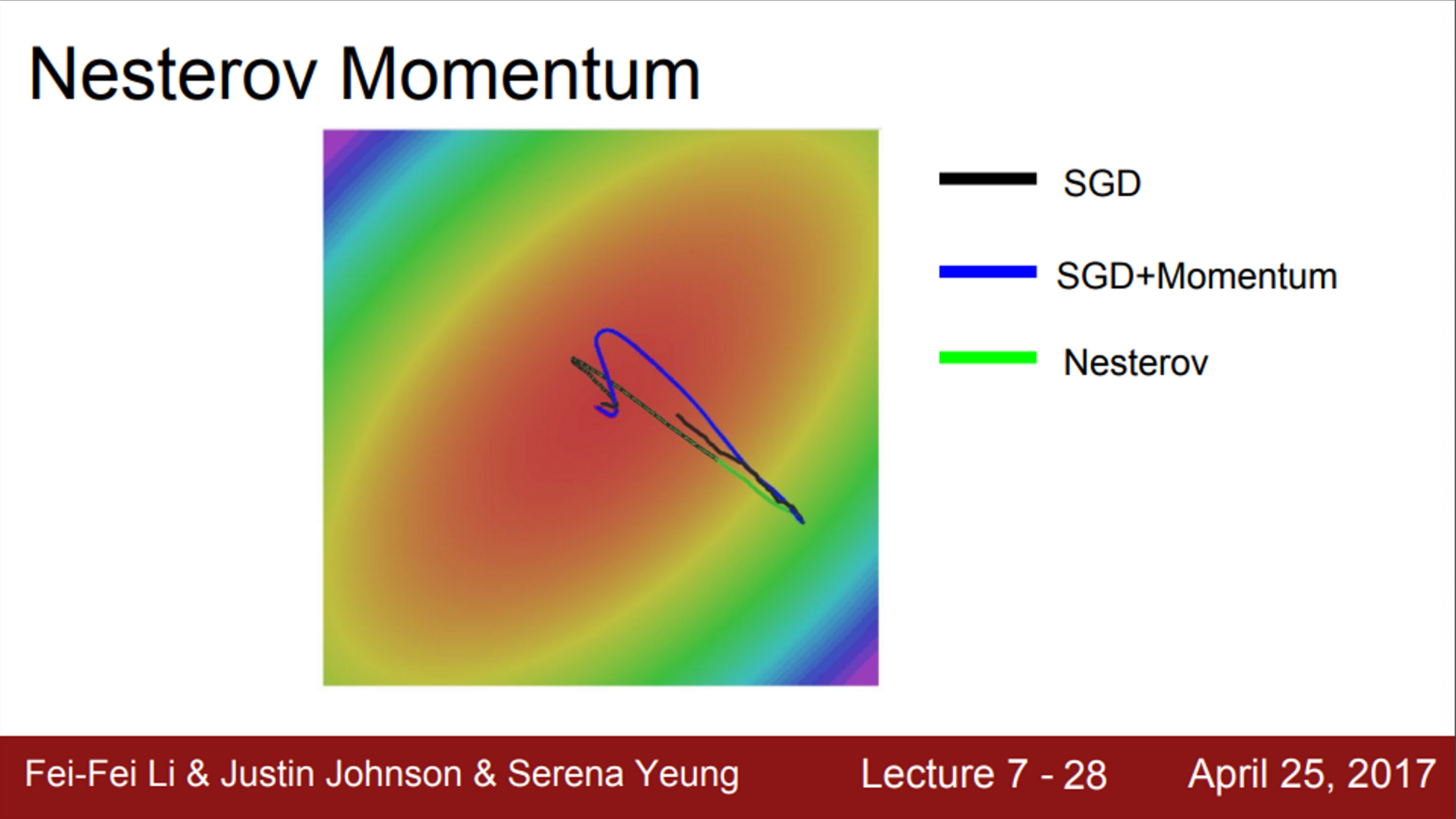
• SGD, Momentum, Nesterov의 예시를 보면,
  • 기본 SGD는 굉장히 느리게 진행
  • momentum 방법들은 minima를 그냥 지나쳐 버리는 경향이 있음
    • 이전의 velocity의 영향을 받기 때문에
    • 하지만, 스스로 경로를 수정하고, minima에 수렴함
  • Nesterov는 momentum에 비해서 overshooting이 덜한 것을 확인할 수 있음

• 다른 최적화 방법 중, AdaGrad도 존재
  • 훈련 도중 계산되는 gradient를 활용하는 방법
    • 기울기의 제곱을 이용하여, 곡면의 변화량을 측정하고 이를 이용하여 learning rate를 조절하는 방식
  • velocity term 대신에 grad squared term을 이용
    • 학습 도중에 계산되는 gradient에 제곱을 해서 계속 더해줌
    • 그 후, update를 할 때, update term을 앞서 계산한 gradient 제곱 항으로 나눠줌

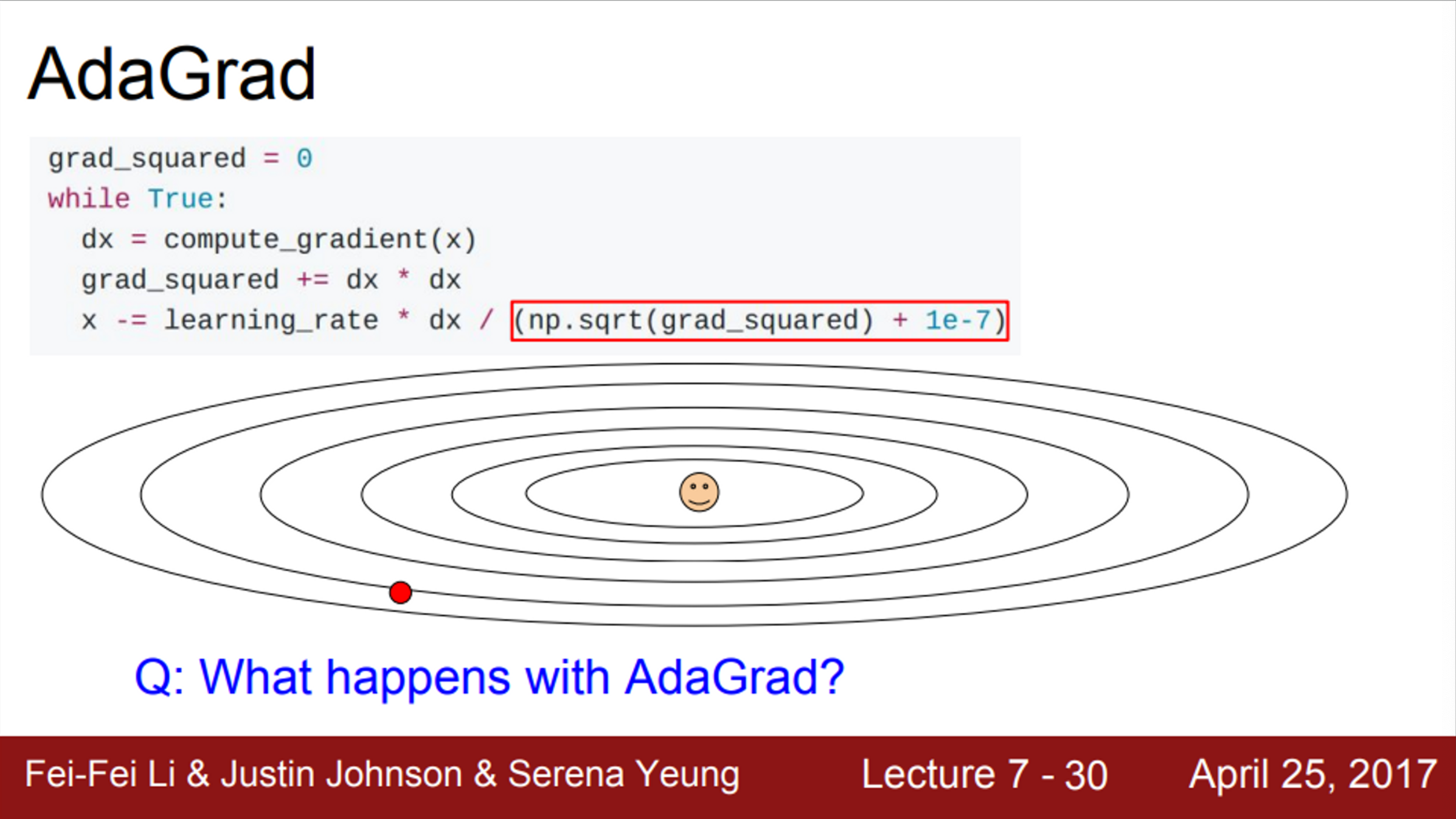
• condition number인 경우, 빨간색 박스 안의 값은 어떨까?
  • 2차원 좌표가 있다고 가정
    • 그 중 한 차원은 항상 gradient가 높은 차원, 다른 하나는 항상 작은 gradient를 가짐
    • Small dimension에서는 gradient 제곱 값의 합이 작고, 이 작은 값이 나눠지므로, 가속도가 붙게 됨
    • Large dimension에서는 gradient가 큰 값이므로, 큰 값이 나눠지게 되고, 속도가 점점 줄어듦

• AdaGrad의 문제는, step을 진행할수록 값이 점점 작아짐
  • update 동안 gradient의 제곱이 계속 더해짐
    • 즉, grad_squared 값이 계속 커짐
  • 분모항이 커지기 때문에, step size를 점점 더 작은 값이 되게 함
  • 손실 함수가 convex한 경우, step size가 점점 작아지는 것은 좋은 특징이 될 수 있음
    • minima에 근접하면, 서서히 속도를 줄여서 수렴할 수 있게 하면 좋음
  • non-convex case에서는, step size가 점점 작아지는 것이 문제가 될 수 있음
    • 가령, saddle point에 걸렸을 때, AdaGrad는 멈춰버릴 수 있음

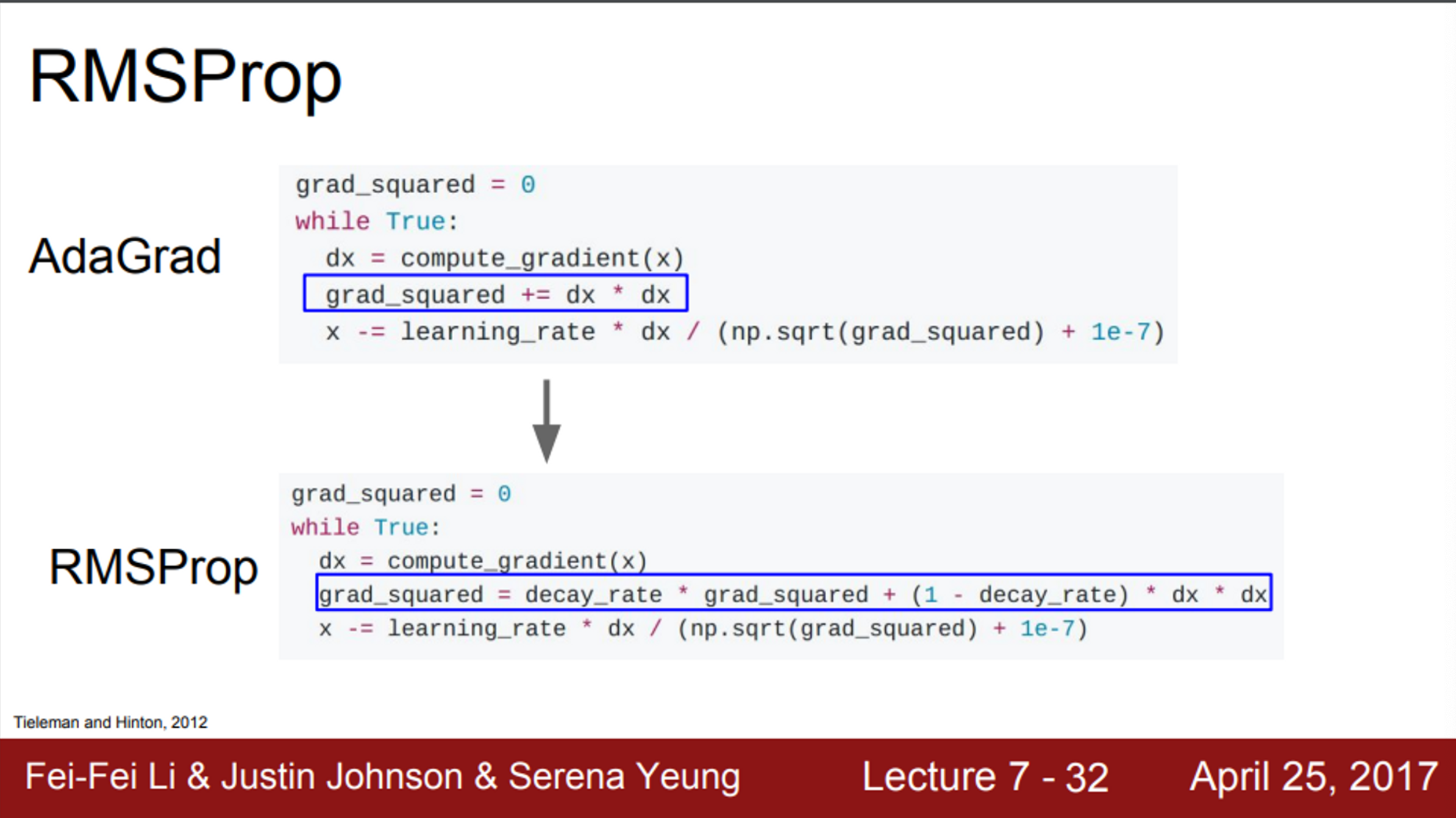
• 앞서 언급한 AdaGrad의 문제를 개선시킨 방법이 RMSProp
  • RMSProp에서는, AdaGrad의 gradient 제곱 항을 그대로 사용함
    • 하지만, 이 값들을 그냥 누적시키는 것이 아니라, 기존의 누적 값에 decay_rate를 곱하고, 현재 gradient의 제곱에는 (1-decay_rate)를 곱해서 더해줌
  • RMSProp은 gradient 제곱을 계속 나눠준다는 점에서 AdaGrad와 유사함
  • 이를 이용하여 step의 속도를 가속/감속 시킬 수 있음
    • 즉, 속도가 점점 줄어드는 AdaGrad의 문제를 해결

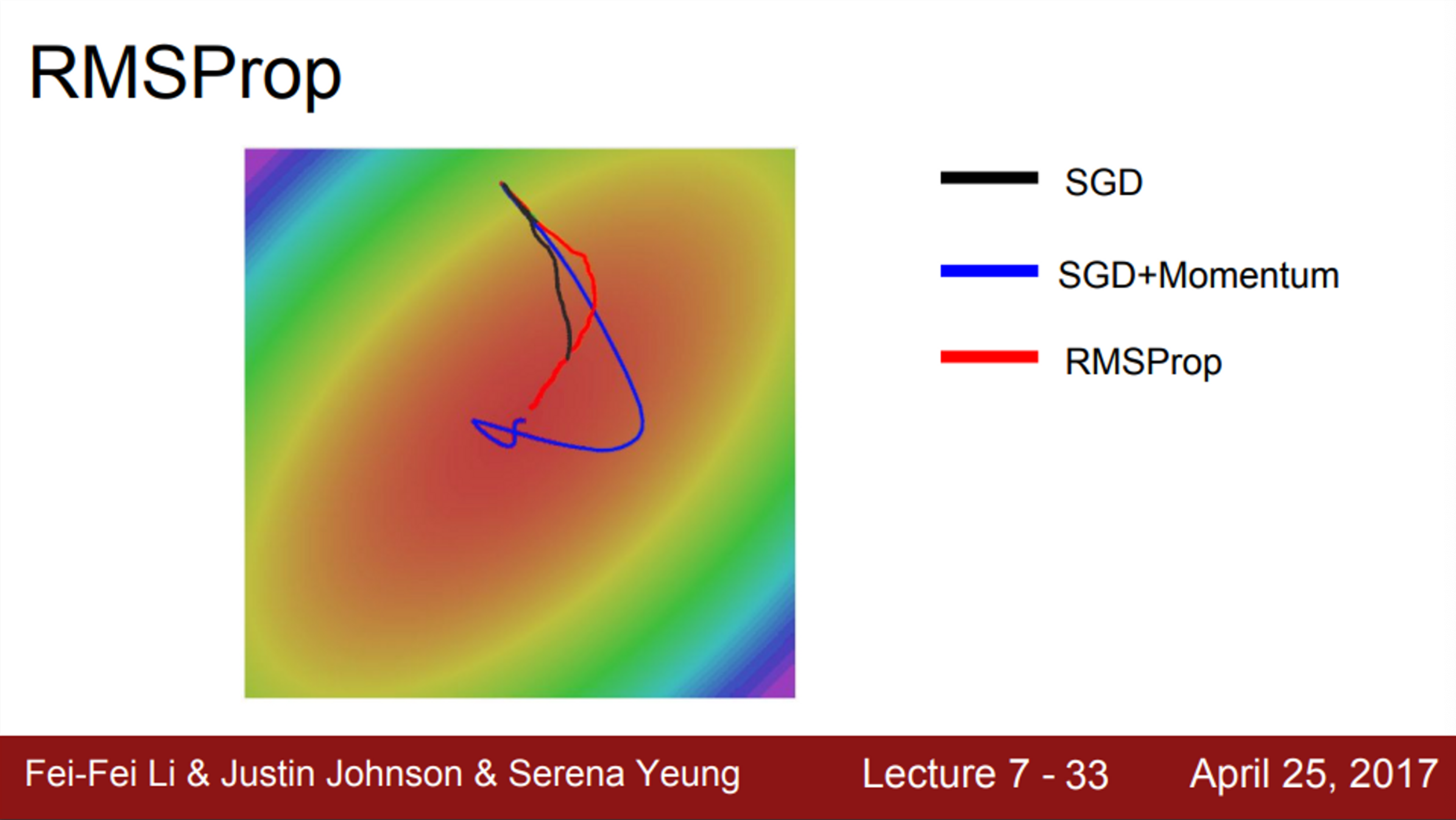
• RMSProp, momentum 방식은 기본 SGD보다 훨씬 더 좋음
• 그러나, 둘의 행동 양식은 다름
  • momentum의 경우, overshooting한 뒤, 다시 minima로 돌아옴
  • RMSProp은, 각 차원마다의 상황에 맞도록 적절하게 궤적을 수정시킴
• 일반적으로 Neural Network를 학습시킬 때, AdaGrad를 잘 사용하지 않음

• 지금까지 살펴본 optimizer는 크게 2가지 방식이 존재
  • momentum을 이용하는 방식
    • velocity를 이용해서 step 사이즈를 조절
  • 훈련 도중 계산된 gradient를 사용하는 방식
    • gradient의 제곱으로 나눠서 step 사이즈를 조절
• 위 2가지 방식을 함께 이용하면 어떨지?
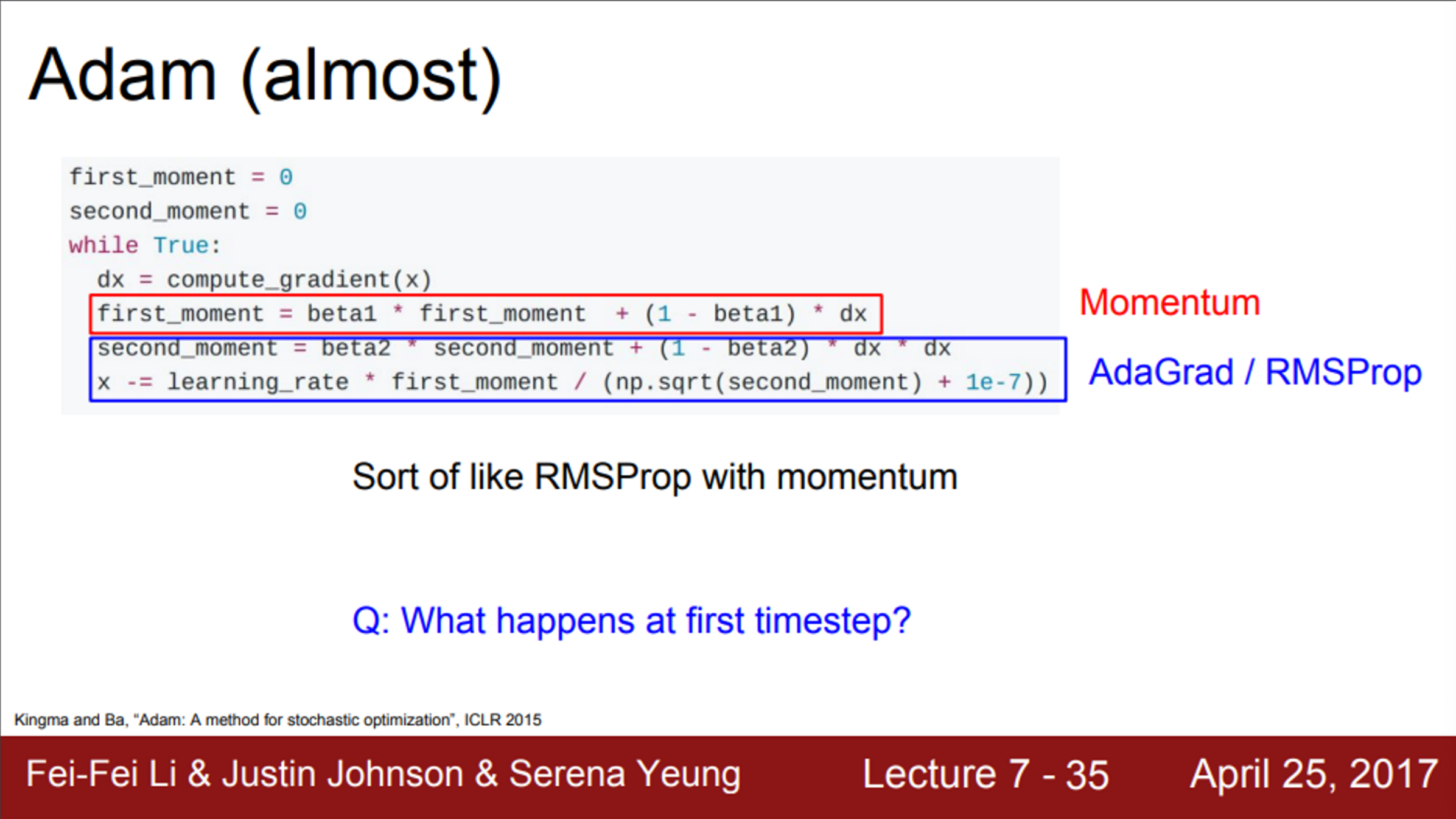
  • 2가지 방식을 함께 이용하는 Adam 알고리즘
    • 위 슬라이드는 Adam과 유사한 알고리즘
    • Adam은 first moment와 second moment를 이용해서, 이전의 정보를 유지시킴
    • 빨간색 first moment는 gradient의 가중 합
    • 파란색 second moment는 gradient의 제곱을 이용하는 방법 (AdaGrad, RMSProp 처럼)
    • Adam으로 update를 진행하게 되면, 우선 first moment는 velocity를 담당
    • 그 후, sqrt(second moment)를 나눠줌
    • 즉, Adam은 momentum + sqrt(gradient) (momentum + RMSProp)
    • 두 종류의 유용한 특징을 모두 이용하는 것
  • 그러나, 여기에도 문제가 존재함
    • 초기 step에서는 second moment를 0으로 초기화함
    • 이때 사용하는 beta2는 decay_rate로 0.9(혹은 0.99) 값으로, 1에 가까운 값을 사용함
    • 따라서, 1회 업데이트 이후에도, second moment는 여전히 0에 가까운 값임
    • 마지막 update step에서, second moment로 나눠주기 때문에, 초기 step이 엄청나게 커짐
    • 중요한 점은, step이 커진 이유가 손실 함수가 가파르기 때문이 아니라는 점 (second moment를 0으로 초기화했기 때문에 발생하는 인공적인 현상)
    • 물론, 초기 first moment도 작은 값이기 때문에, second moment의 작은 값과 만나서 서로 상쇄시킬 수 있지만, 간혹 위와 같은 현상이 발생하는 경우도 존재함 (위 현상은 굉장히 나쁜 상황)

• 실제 Adam에서는, 위와 같은 현상을 해결하기 위해서, 보정하는 항을 추가함 (bias correction term)
  • first/second moment를 update하고 난 후, 현재 step에 맞는 적절한 unbiased term을 계산
  • 실제 Adam은 first/second moment만 계산하는 것이 아니라, unbiased term을 함께 넣어줘야 함
• Adam은 다양한 문제들에서 잘 작동하기 때문에, 많이 사용함

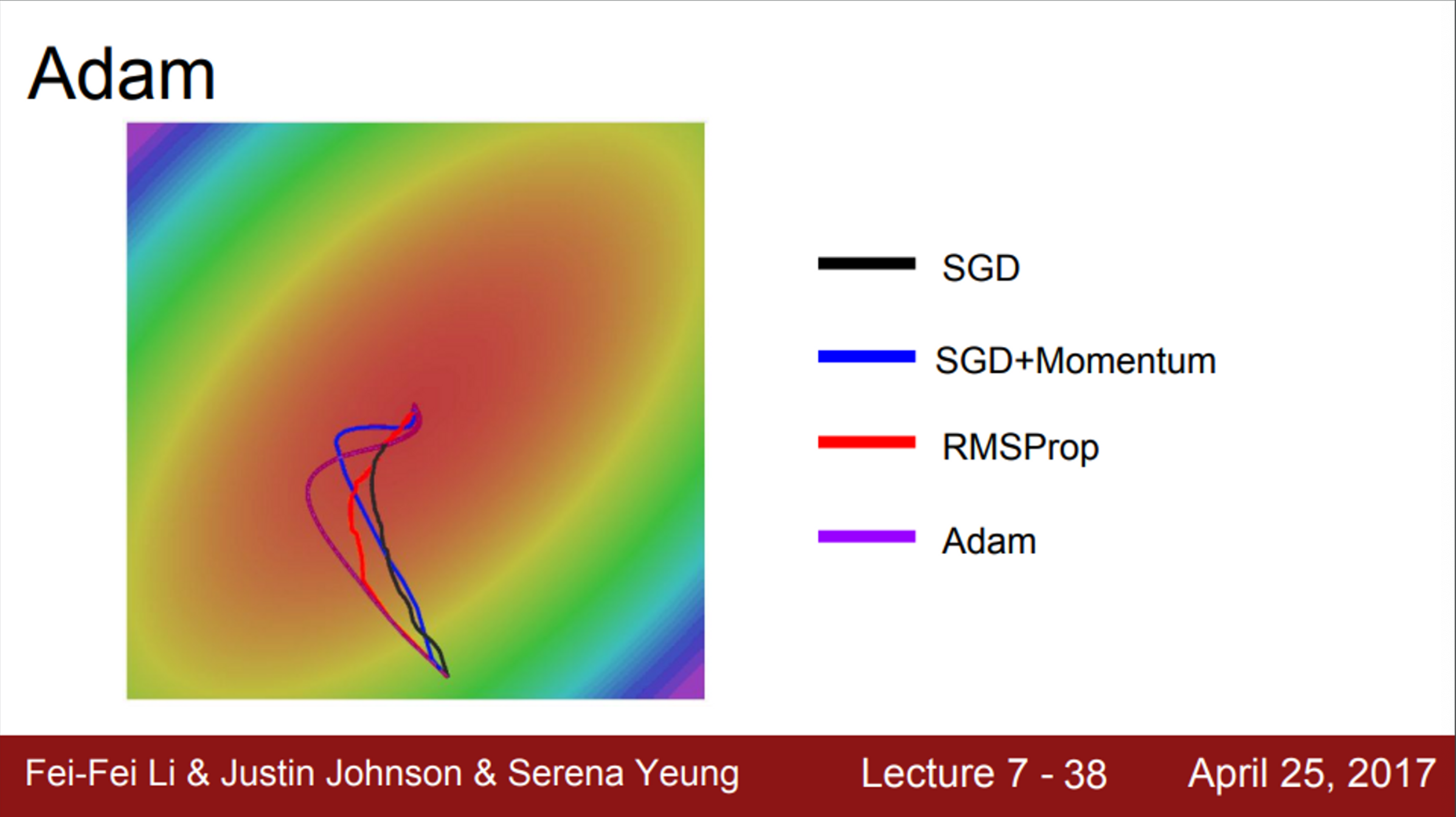
• Adam은 momentum처럼 overshooting이 일어나긴 하지만, 심하진 않음
• 또한, Adam은 RMSProp과 같은 특징도 가지고 있음
  • 각 차원의 상황을 따로 고려해서 step을 이동
• 즉, Adam은 momentum스러우면서도, RMSProp스럽다는 것

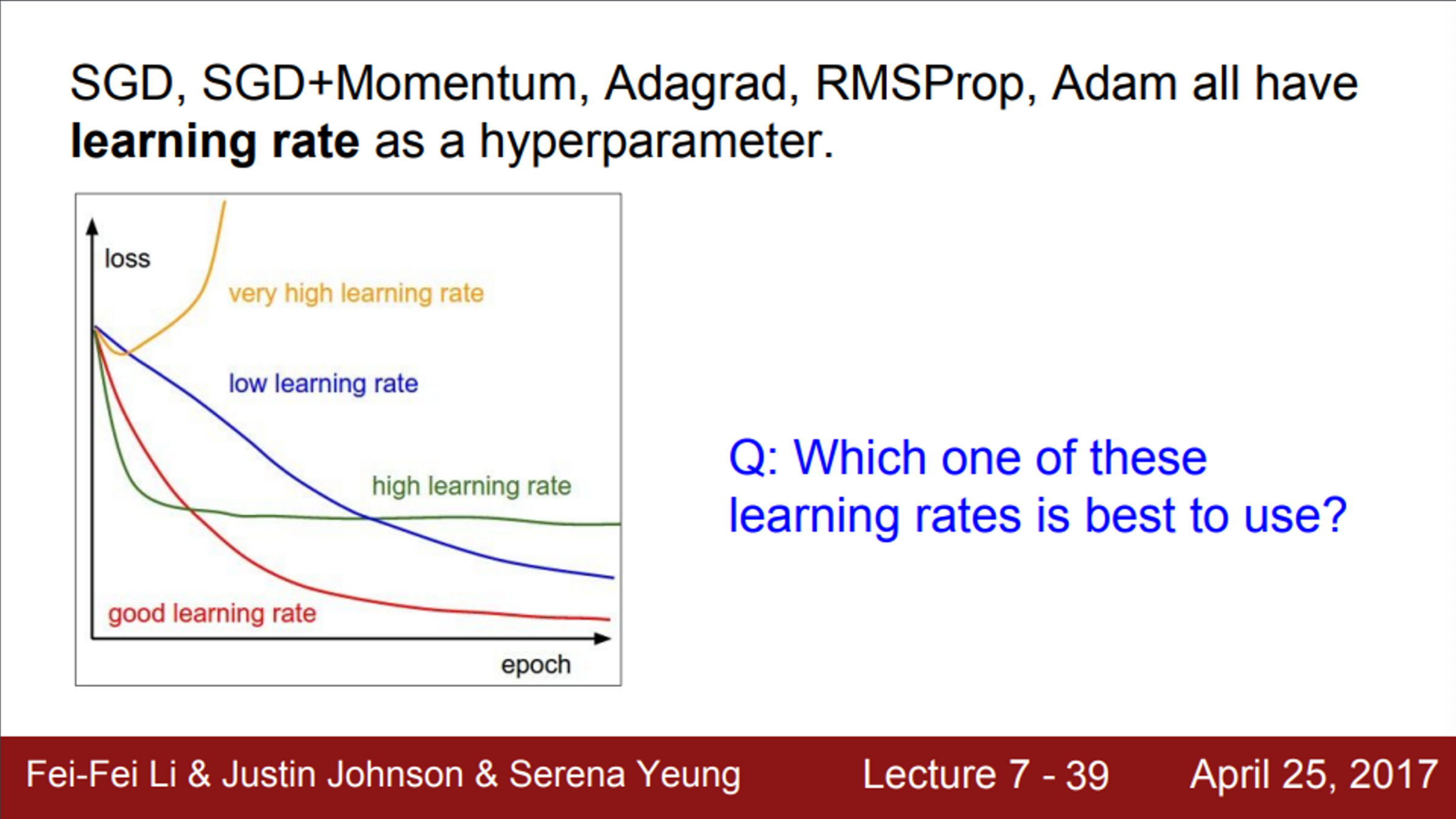
• 지금까지 본 모든 Optimization 알고리즘은 learning rate라는 하이퍼파라미터를 가지고 있었음
  • Learning rate가 지나치게 높으면, Loss는 노란색처럼 솟구침
  • Learning rate가 너무 낮으면, 파란색처럼 수렴하는데 오래 걸림
  • 우리는 학습 과정에서 learning rate를 하나 정해놓고 시작해야 하기 때문에, 적절한 learning rate를 고르는 것이 중요함 (하지만 어려운 일)

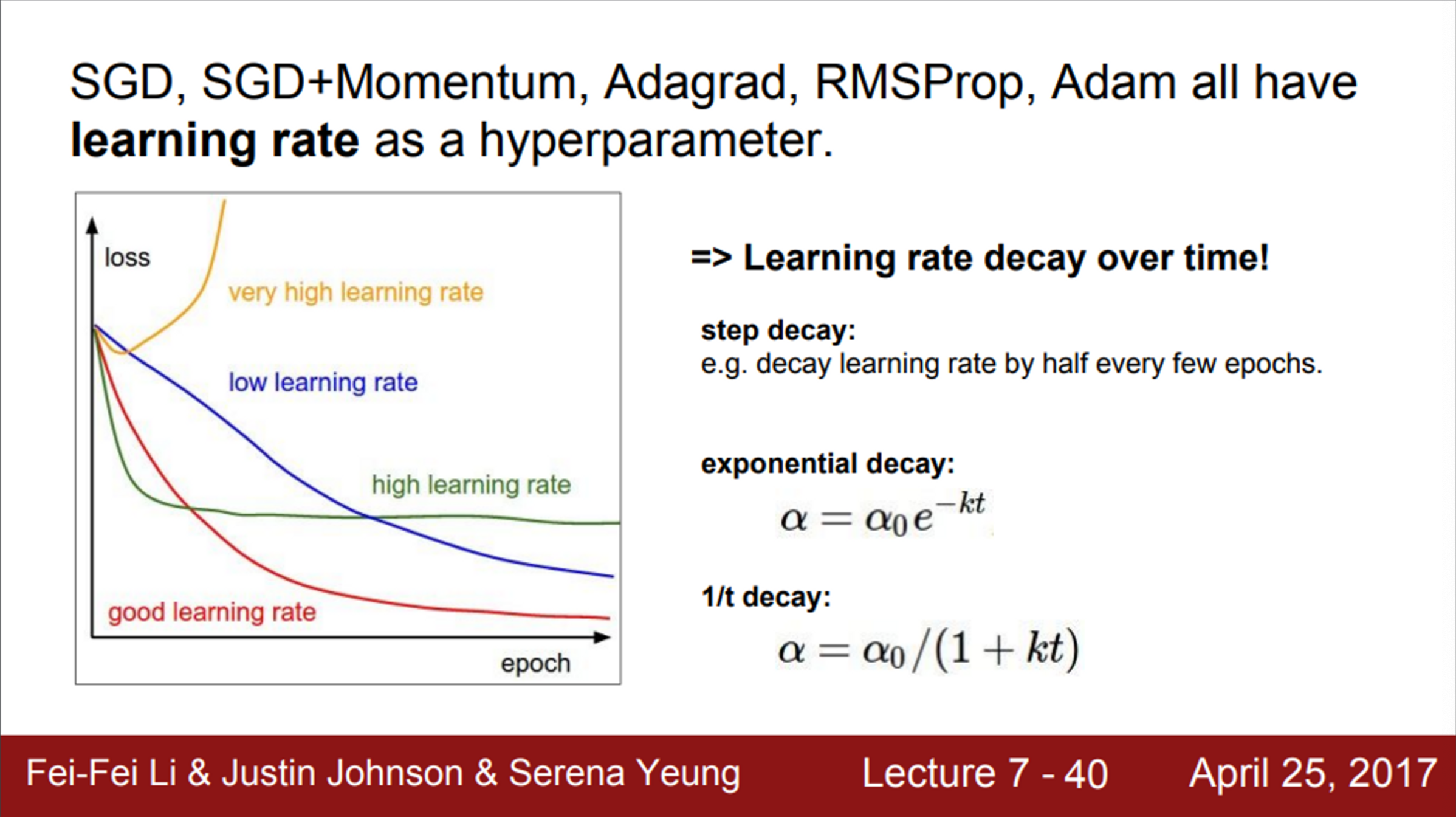
• 적절한 learning rate를 선택하기 위해서, learning rates decay 전략을 사용할 수 있음
  • 각각의 learning rate의 특성을 적절히 이용하는 것
  • 처음에는 learning rate를 높게 설정한 다음, 학습이 진행될수록 learning rate를 점점 낮추는 것
  • 다양한 전략을 시도해볼 수 있지만,
    • 가령, 100,000 iter에서 learning rate를 낮추고 학습 (step decay)
    • 혹은, 학습 과정에서 learning rate를 꾸준히 낮출 수도 있음 (exponential decay)

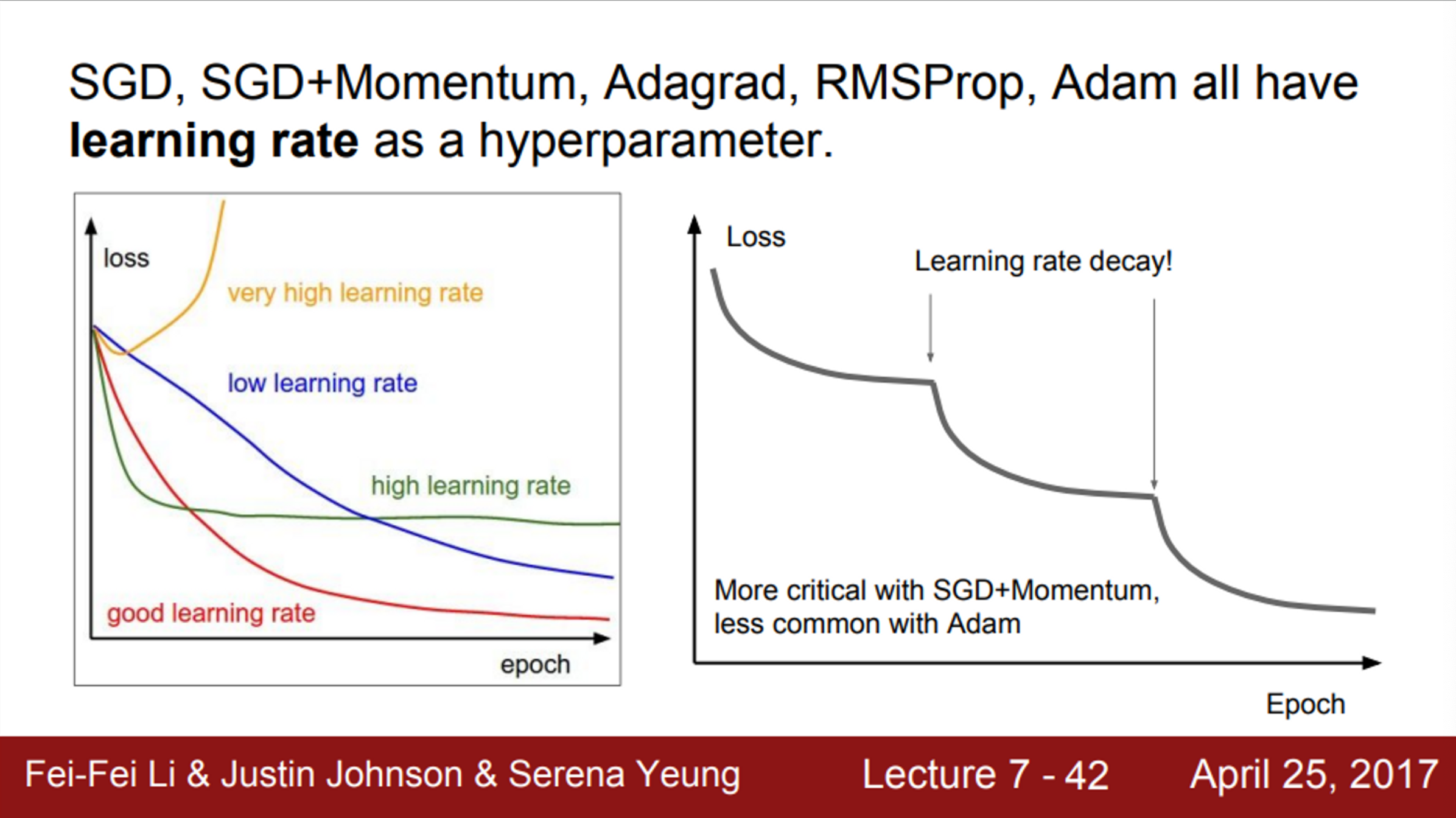
• 오른쪽 그림은 ResNet 논문에 있는 그림
  • Loss가 계속 내려가고 있는데, 해당 논문에서는 step decay learning rate 전략을 사용함
    • 평평해지다가 갑자기 내려가는 구간이 learning rate를 낮추는 구간
  • learning rate를 언제 낮춰야 하는지 생각해보면,
    • 수렴을 잘 하고 있는 상황에서, gradient가 점점 작아지고 있음
    • 이 상황에서 learning rate를 낮추게 되면, 속도가 줄어들 것이고, 지속해서 loss가 내려갈 수 있을 것임
• learning rate decay는 Adam보다 SGD momentum을 사용할 때 자주 사용함
• 보통 학습 초기에는, learning rate decay가 없다고 생각하고, learning rate를 잘 선택하는 것이 중요함
  • learning rate decay를 설정하는 순서는,
    • 우선 decay 없이 학습을 진행
    • 이후 Loss curve를 살피고 있다가, decay가 필요한 곳이 어디인지 고려해 보는 것이 좋음

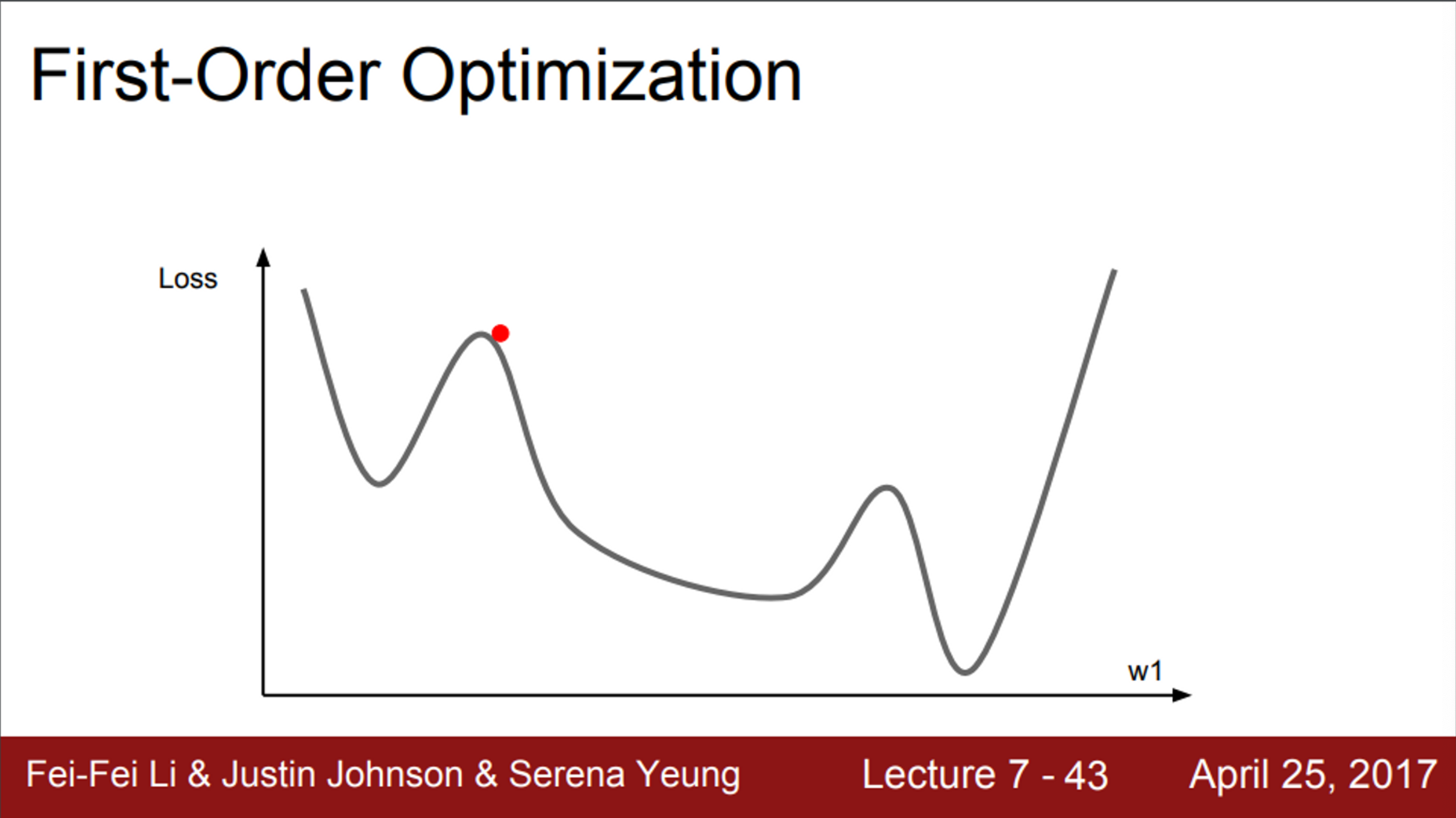
• 지금까지 배운 Optimization 알고리즘들은 모두 1차 미분을 활용한 방법

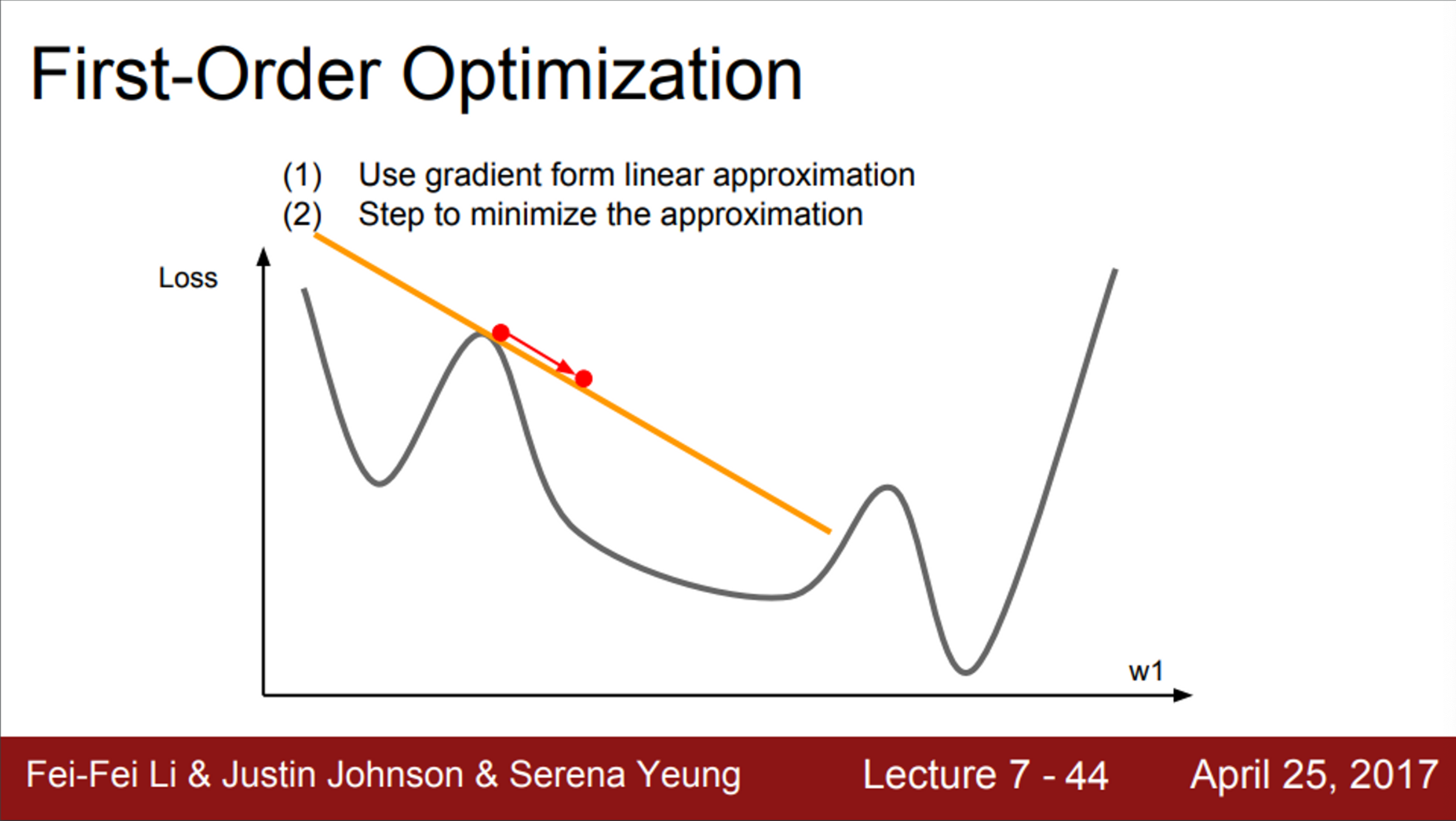
• 그림처럼 1차원의 손실 함수가 있다고 생각해보면,
  • 현재 우리는 빨간색 점에 위치해 있음
  • 이 지점에서의 gradient를 계산
  • 이 gradient 정보를 이용해서, 우리는 손실 함수를 선형 함수로 근사시킴
  • 이 1차 근사 함수를 실제 손실 함수라고 가정하고 step을 내려갈 것임
    • 하지만, 이 근사 함수로는 멀리 갈 수 없음

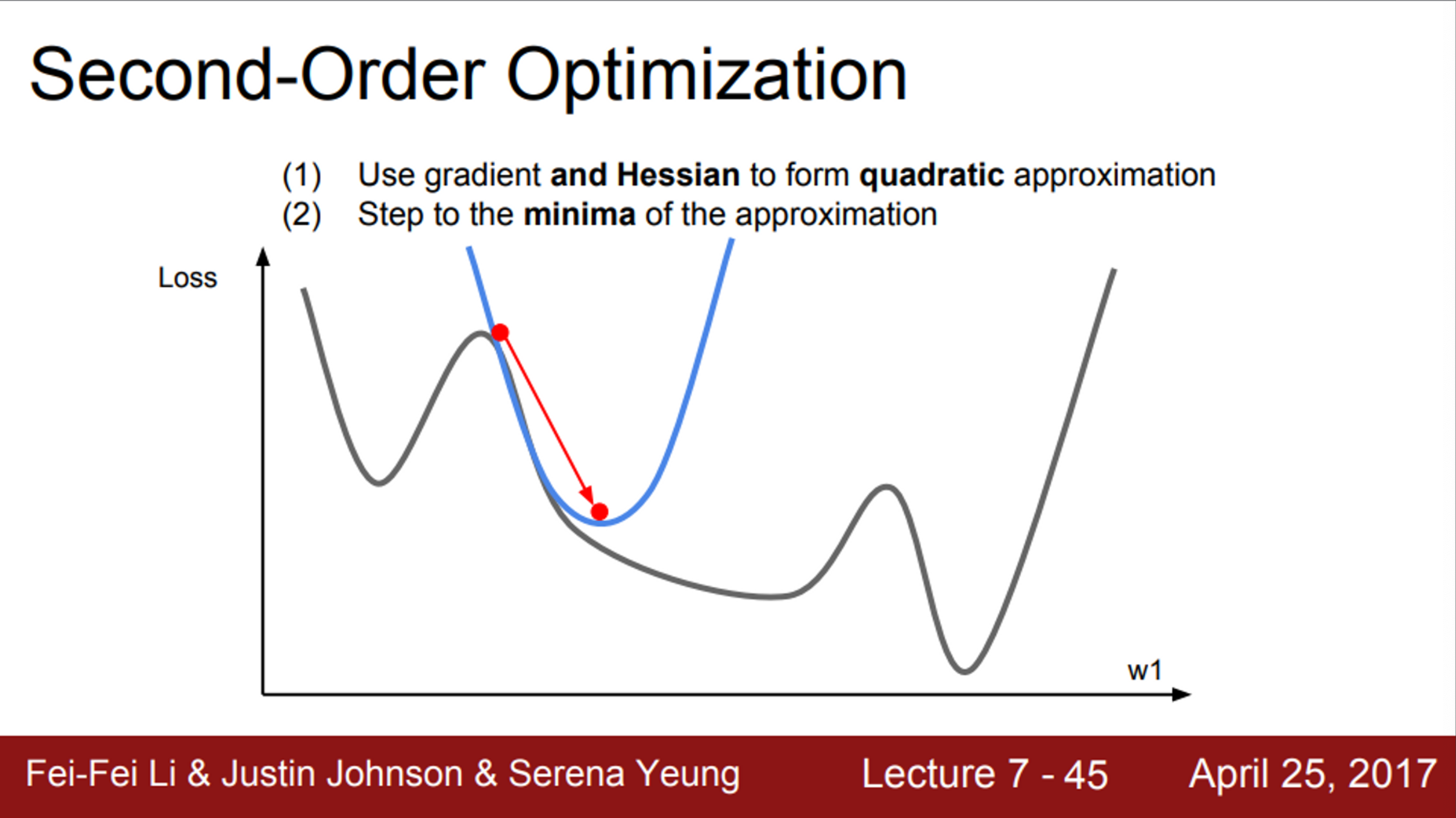
• 2차 근사의 정보를 추가적으로 활용하는 방법
  • 2차 테일러 근사 함수가 될 것이며, 2차 함수의 모양
  • 2차 근사를 사용하면, minima에 더 잘 접근할 수 있음
    • 이것이 2nd-order optimization의 기본 아이디어

• 방금의 예시를 다차원으로 확장시키면, Newton step이라고 함
  • Hessian matrix를 계산 (2차 미분 값들로 된 행렬)
  • Hessian matrix의 역행렬을 이용하게 되면, 실제 손실 함수의 2차 근사를 이용해 minima로 곧장 이동할 수 있을 것임
• 이 알고리즘이 특이한 점은?
  • 적어도, 기본적인 Newton’s method에서는 learning rate가 불필요
  • 하지만, 실제로는 learning rate가 필요함
    • 2차 근사도 minima로 이동하는 것이 아니라, minima의 방향으로 이동하는 것 이기 때문에

• 그러나, Deep learning에서는 사용할 수 없음
  • Hessian matrix는 $N\times N$ 행렬
    • N은 Network의 파라미터 수
    • 따라서, 이를 메모리에 저장할 방법이 없고, 역행렬 계산도 불가능

• 그래서 실제로는, quasi-Newton methods를 이용
  • Full Hessian을 그대로 사용하는 것이 아니라, 근사시켜서 사용
    • Low-rank approximation 하는 방법

• L-BFGS도 2nd-order optimizer
  • 이 방법도 Hessian을 근사시켜서 사용하는 방법
  • 사실상 DNN에서는 잘 사용하지 않음
    • L-BFGS에서 2차 근사가 stochastic case에서 잘 동작하지 않기 때문에
    • 또한, L-BFGS는 non-convex problem에도 적합하지 않음

• 실제로는 Adam을 가장 많이 사용
  • 그러나, full batch update가 가능하고, stochasticity가 적은 경우라면, L-BFGS가 좋은 선택이 될 수 있음
    • L-BFGS가 Neural Network를 학습시키는데 많이 사용되지는 않지만, style transfer와 같은 알고리즘에 종종 사용할 수 있음

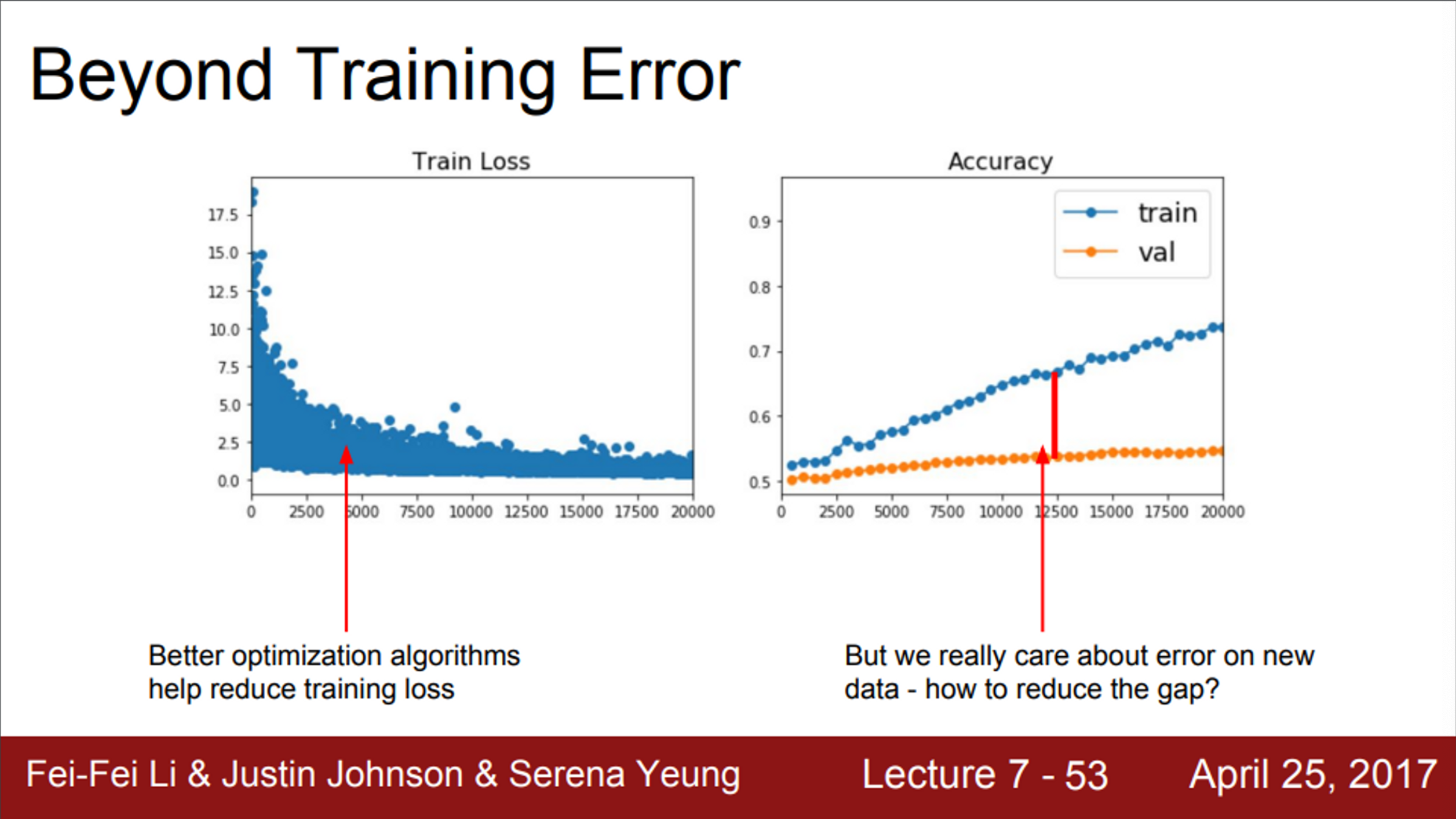
• 지금까지의 내용은, 전부 training error를 줄이기 위한 방법이었음
• Optimization 알고리즘들은 training error를 줄이고, 손실 함수를 최소화 시키기 위한 역할을 수행
  • 그러나, 사실 우리는 training error에 크게 신경쓰지 않음
  • 우리가 원하는 것은, train/test error의 격차를 줄이는 것
    • 그렇다면, 손실 함수 최적화를 이미 모두 끝마친 상황에서, 한번도 보지 못한 데이터에서의 성능을 올리기 위해서는 어떻게 해야하는지?

• 가장 빠르고, 쉬운 방법은 모델 앙상블
  • Machine learning 분야에서 종종 사용하는 기법
  • 여러가지 모델을 독립적으로 학습시킨 후, 이 모델들 결과의 평균을 결과로 이용하는 방법
  • 모델의 수가 늘어날수록, overfitting도 줄어들고, 성능도 조금씩 향상됨

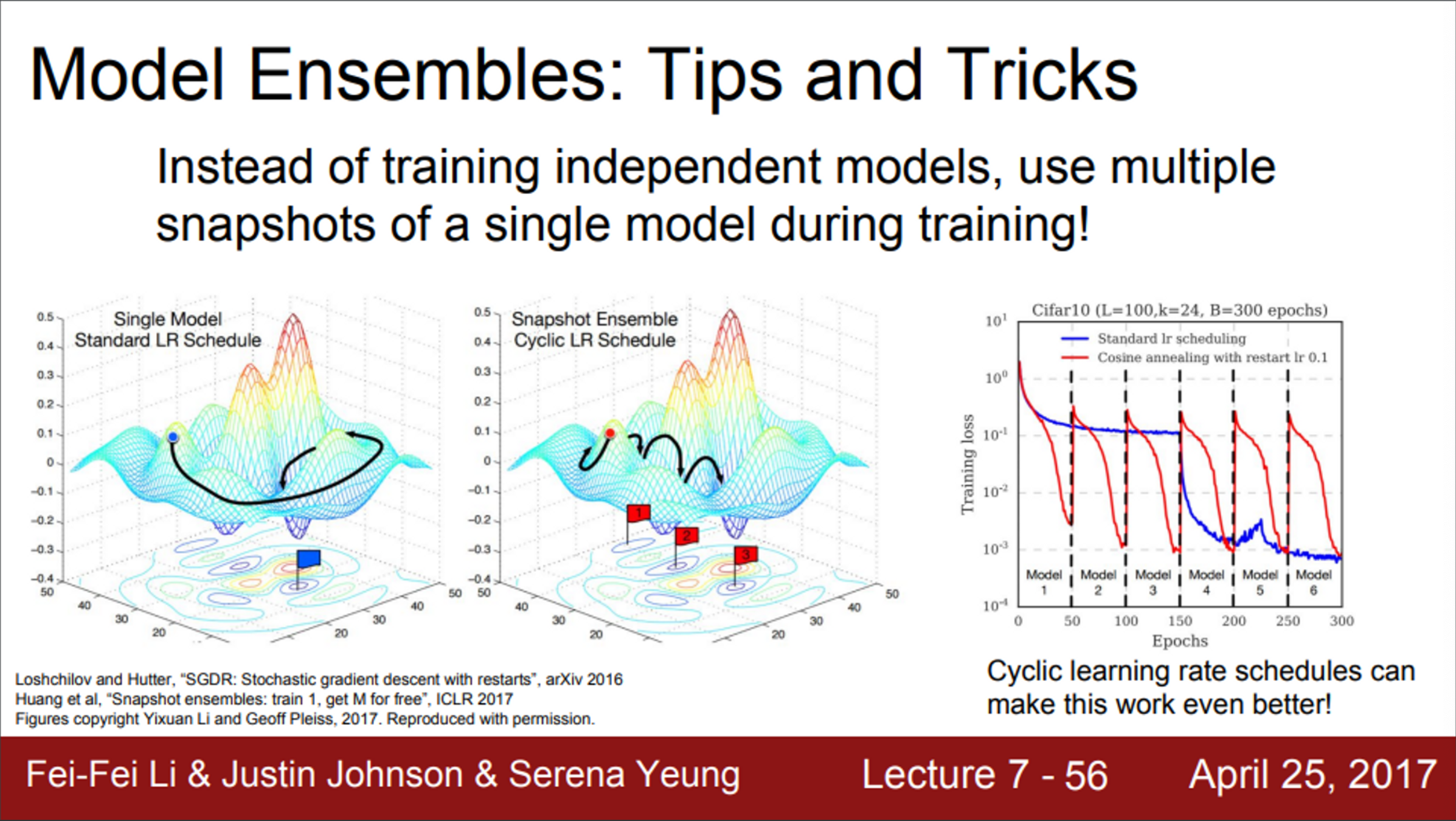
• 모델을 독립적으로 학습시키는 방법이 아닌, 학습 도중 중간 모델들을 저장하고 앙상블로 사용하는 방법도 존재
  • test time에는 여러 snapshot에서 나온 예측값들을 평균을 내서 사용함
• 좀 더 향상된 알고리즘도 존재
  • 독특한 learning rate 스케줄을 이용하는 방법
  • Learning rate를 엄청 낮췄다가, 다시 엄청 높혔다가를 반복
    • 이 논문의 아이디어는, 이런 방식으로 손실 함수의 다양한 지역에 수렴할 수 있도록 만들어줌
    • 이런 앙상블 기법으로 모델을 한번만 train시켜도 좋은 성능을 얻을 수 있게 하는 방법

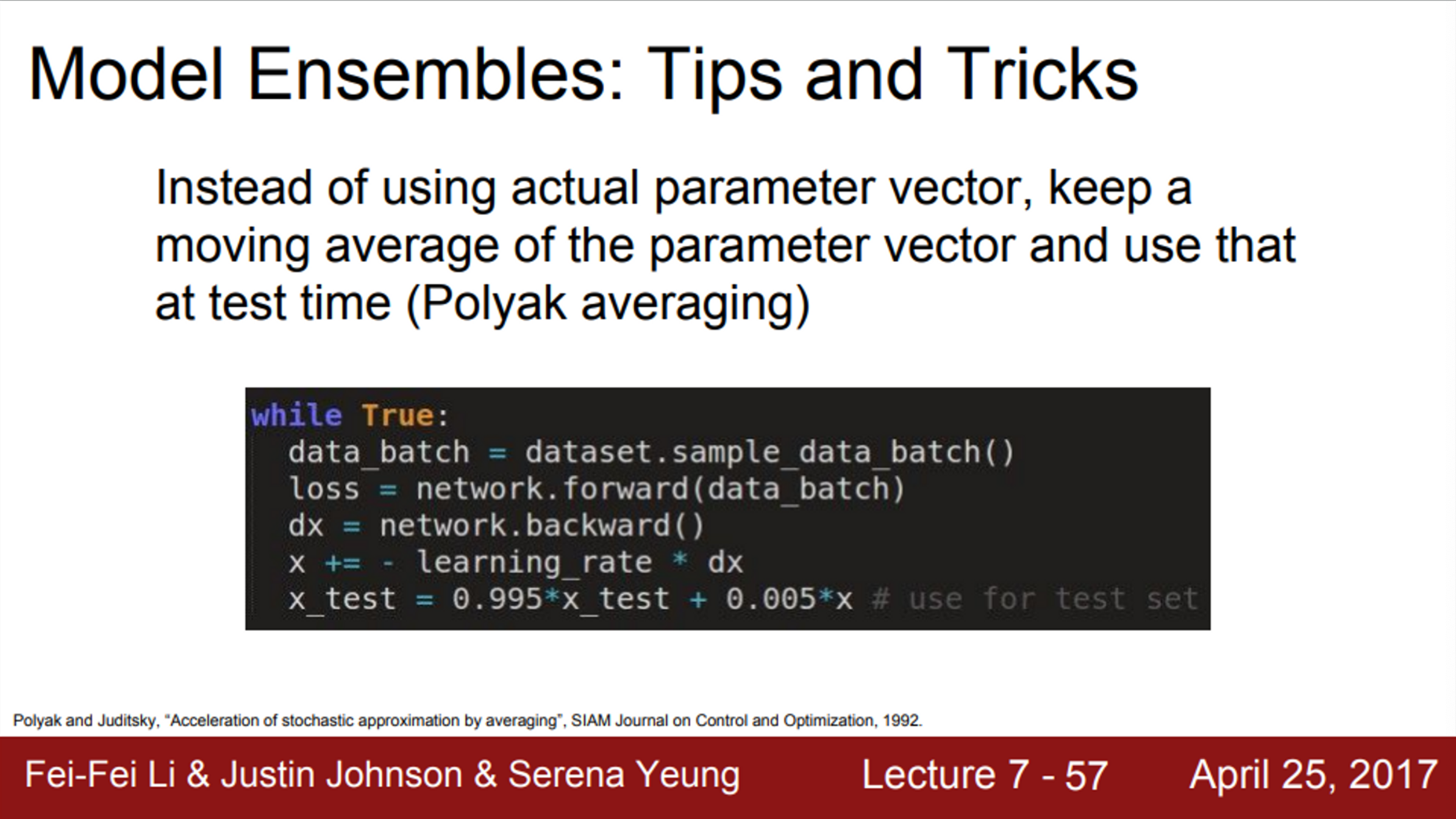
• 또 다른 방법으로는, 학습하는 동안에 파라미터의 exponentially decaying average를 계속 계산
  • 이 방법은 학습 중인 Network의 smooth ensemble 효과를 얻을 수 있음
  • checkpoints에서의 파라미터를 그대로 쓰지 않고, smoothly decaying average를 사용하는 방법
    • 이를 Polyak averaging 이라고 함
    • 때때로 조금의 성능 향상을 보일 수 있음
  • 시도해볼만한 방법이긴 하지만, 실제로 자주 사용하진 않음

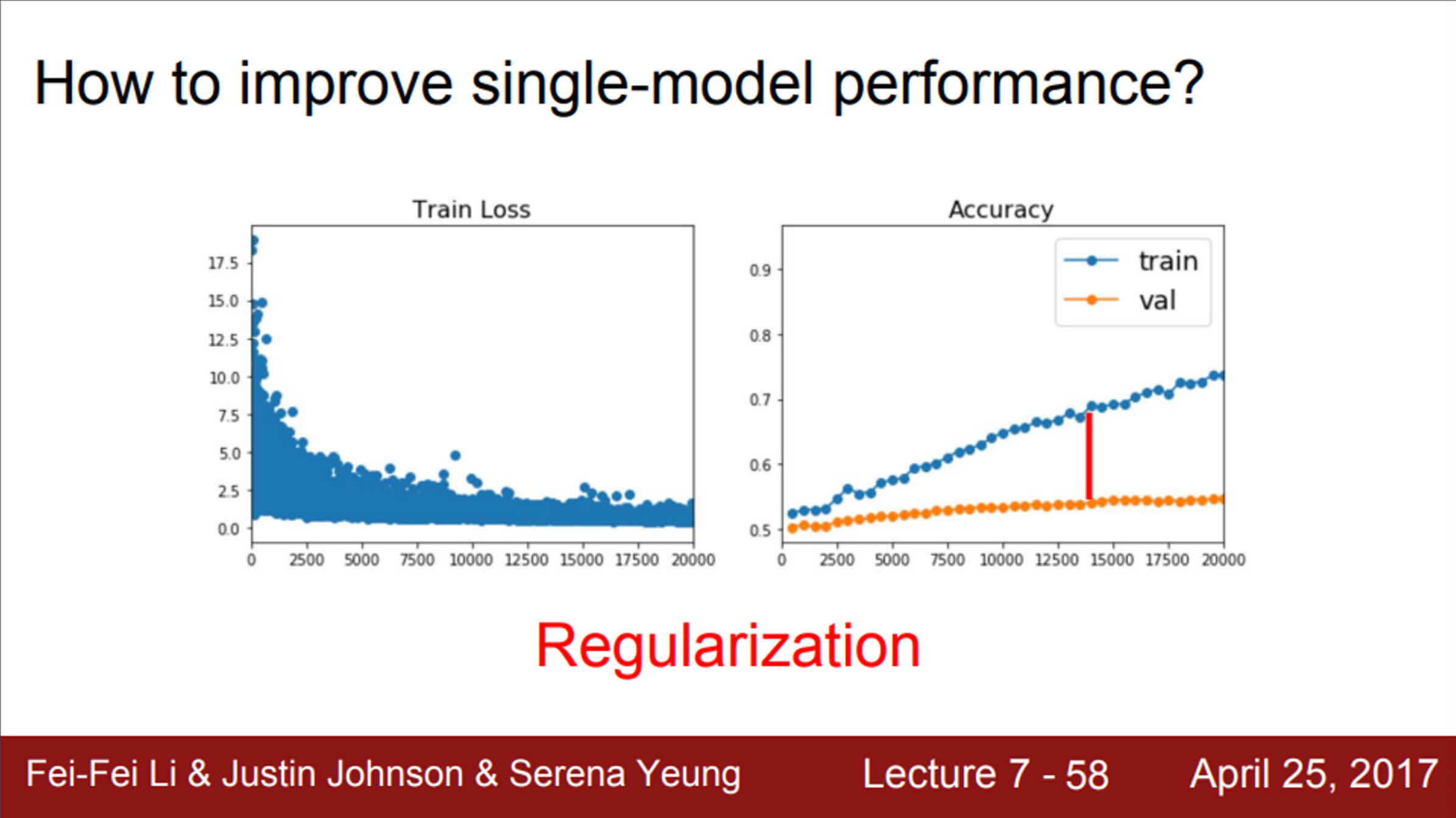
• 그렇다면, 앙상블이 아닌 단일 모델의 성능을 향상시키기 위해서는 어떻게 해야하는지?
  • 우리가 정말 원하는 것은, 단일 모델의 성능을 올리는 것
  • Regularization term을 추가하여, 모델이 training data에 fit하는 것을 막아줄거임
  • 그리고, 한번도 보지 못한 데이터에서의 성능을 향상시키는 방법

• 우리는 이미 몇가지 regularization 기법을 살펴봤음
  • Loss에 추가적인 항을 삽입하는 방법
  • 손실 함수에서 기존의 항은 training data에 fit하려 하고, 다른 하나는 regularization term으로 trainind data에 과도하게 fit되는 것을 막으려고 함
    • L2 regularization이 대표적인 예시
    • 그러나, L2 regularization은 Neural Network에서 잘 사용하지 않음

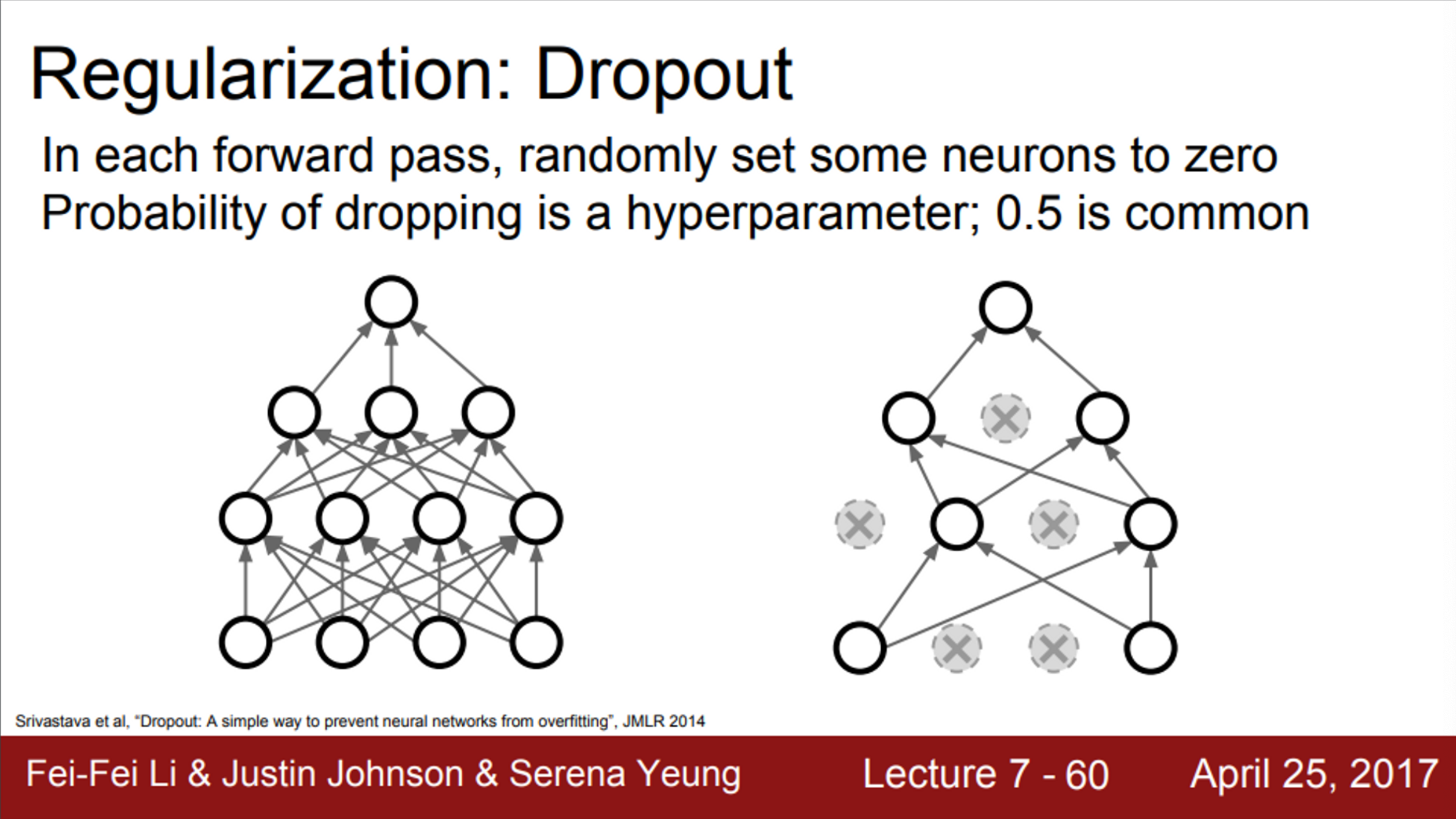
• Neural Network에서 가장 많이 사용하는 regularization은 바로 dropout
  • forward pass 과정에서, 임의로 일부 뉴런을 0으로 만드는 것
  • forward pass를 할때마다, 0이 되는 뉴런이 바뀜
    • dropout은 한 레이어씩 진행
    • 한 레이어의 출력을 전부 구하고, 임의로 일부를 0으로 만듦. 그리고 다음 레이어로 넘어가는 식

• 실제 dropout 구현은 간단함

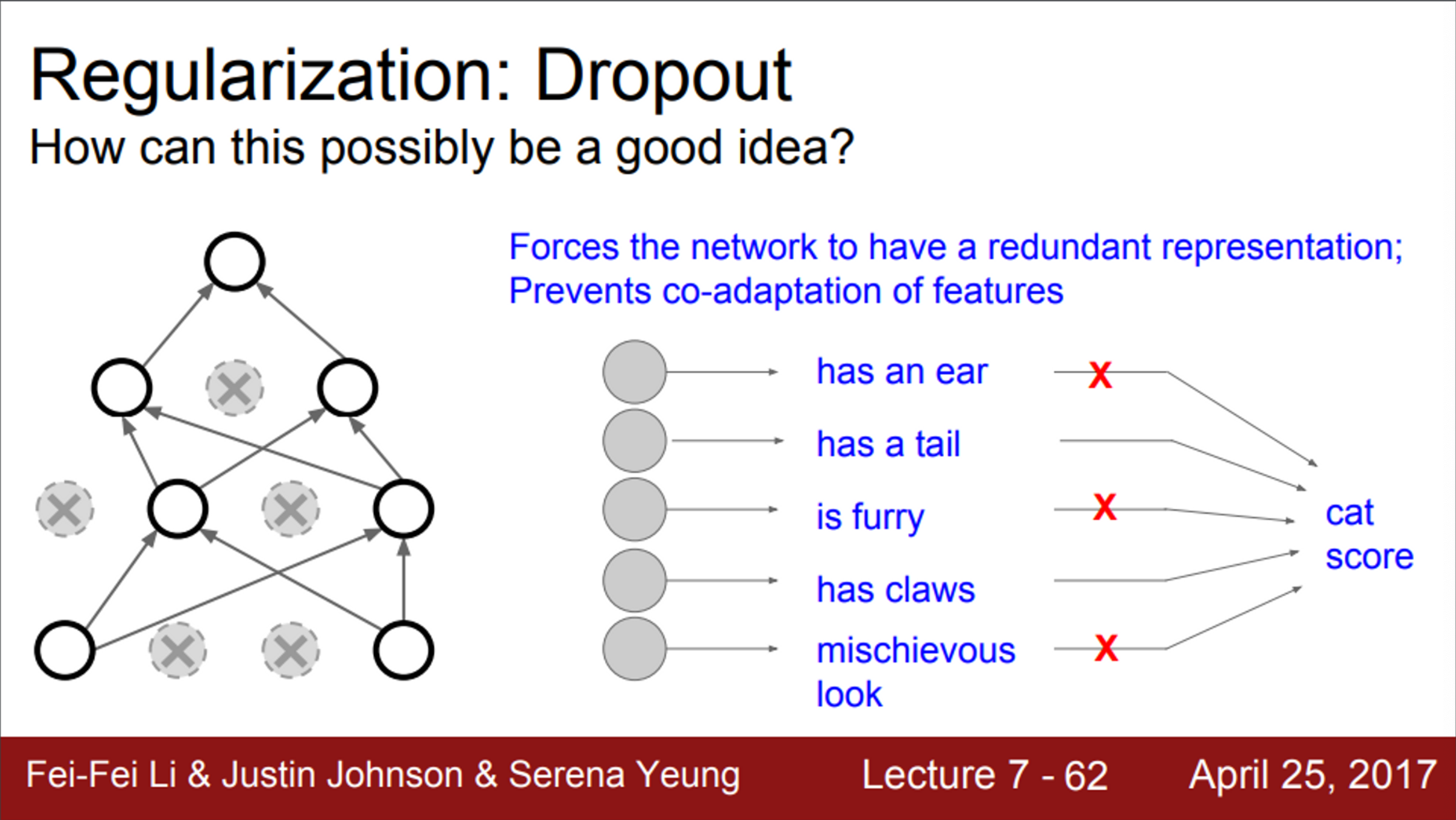
• Dropout이 좋은 이유
  • dropout은 일부 값들을 0으로 만들면서, training time의 Network를 훼손시키고 있음
    • feature들 간의 상호작용(co-adaptation)을 방지한다고 볼 수 있음
    • 즉, 일부 feature에만 의존하지 못하게 해줌
    • 대신, 모델이 예측할 때, 다양한 feature를 골고루 이용할 수 있도록 함
  • 따라서, dropout이 overfitting을 어느정도 막아준다고 할 수 있음

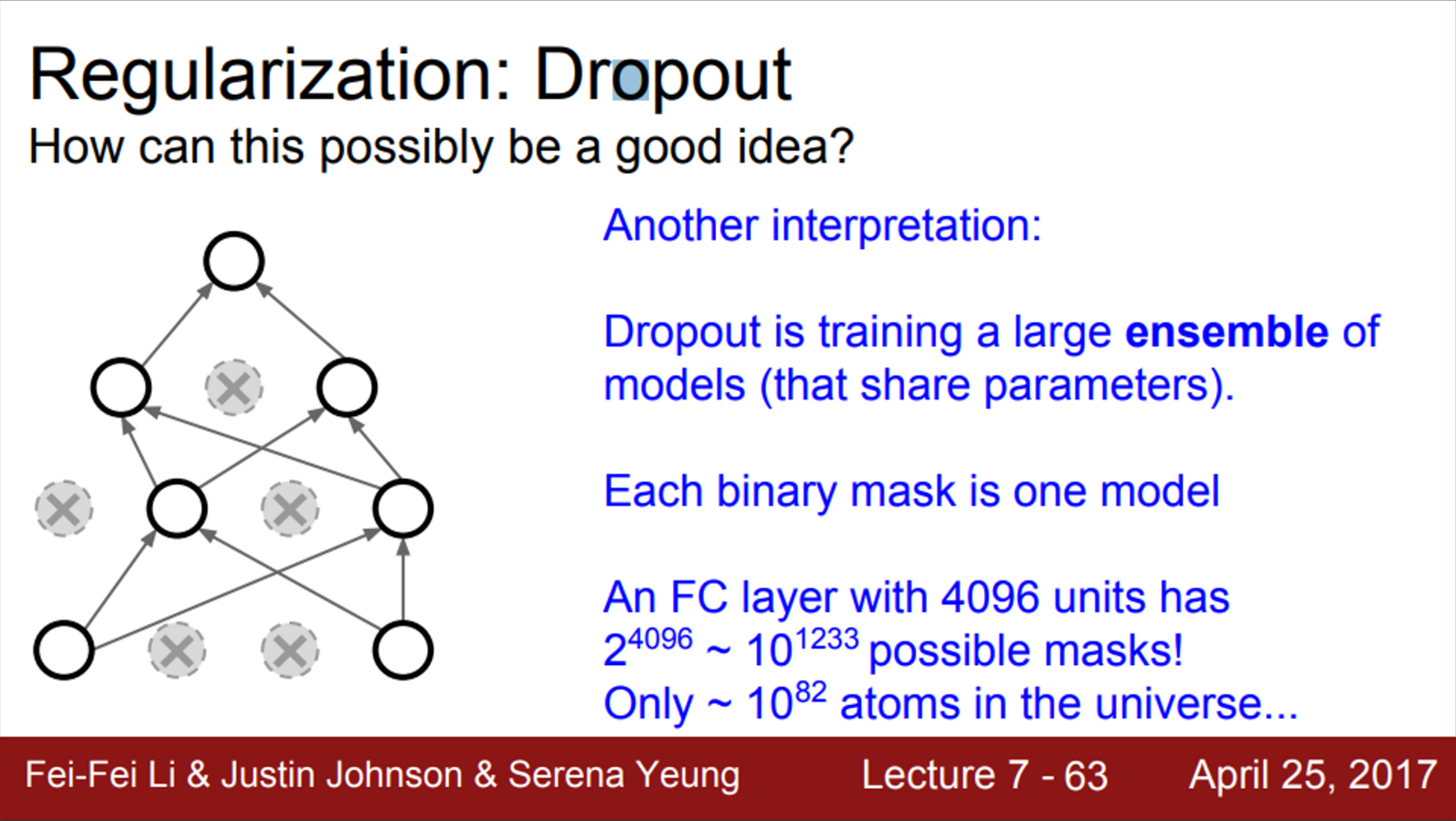
• 또한, 단일 모델로 앙상블 효과를 가질 수 있음
  • Dropout을 적용한 Network는 뉴런의 일부만 사용하기 때문에, sub Network라고 볼 수 있음
  • 또한, dropout을 통해서 만들 수 있는 sub Network 경우의 수는 다양함
  • 따라서, dropout은 서로 파라미터를 공유하는 sub Network 앙상블을 동시에 학습시키는 것이라고 생각할 수 있음
  • 즉, dropout은 아주 거대한 앙상블 모델을 동시에 학습시키는 것이라고 볼 수 있음

• 그렇다면, dropout을 test time에 이용하면 어떻게 될까?
  • dropout을 사용하게 되면, 기본적으로 Neural Network의 동작 자체가 변하게 됨
    • 기존의 Neural Network는 가중치 W와 입력 x에 대한 함수 f 였음
    • Dropout을 사용하게 되면, Network에 z라는 입력이 추가됨 (z는 random dropout mask)
    • z는 임의의 값이고, test time에서 임의의 값을 부여하는 것은 좋지 않음
  • 따라서, Network가 이미 학습된 상태에서, test time에 이러한 임의성을 주는 것은 적절하지 않음
    • 대신 그 임의성(randomness)을 average out 시킴
    • 이는 적분을 통해 randomness를 marginalize out 시키는 것으로 생각해볼 수 있음 (단, 적분이 까다로움)
    • 이 문제를 해결할 수 있는 간단한 방법 중 하나는, 샘플링을 통해서 적분을 근사시키는 것 (이 방법도 randomness를 만들기 때문에, 좋지 않은 방법)

• Dropout의 경우, 일종의 locally cheap한 방법을 이용해서 적분식을 근사할 수 있음
  • 입력이 $x, y$이고, 가중치 $w_1, w_2$, 출력이 $a$인 뉴런이 있다고 할 때,
  • test time에서, $a=w_1x+w_2y$
  • 이 Network에 dropout(p=0.5)를 적용한 후, train을 시킨다고 가정하면, train time에서의 기대값은 다음과 같이 계산할 수 있음
    • $E[a]=\frac{1}{4}(w_1x+w_2t) + \frac{1}{4}(w_1x+0y) + \frac{1}{4}(0x+0t) + \frac{1}{4}(0x+w_2t)$
    • $E[a]= \frac{1}{2}(w_1x+w_2t)$
  • dropout mask에는 총 4가지 경우의 수가 존재
    • 따라서, 그 값들을 4개의 mask에 대해 평균화 시켜 줌
  • test/train time간의 기대값이 서로 다름 (train time의 기대값이 test time의 절반)
• test time에서 stochasticity를 사용하지 않고 할 수 있는 방법 중 하나는, dropout probablilty를 Network의 출력에 곱해주는 방법
  • 실제로 많은 사람들이 Dropout을 사용할 때, 이 방법을 많이 사용함

• Dropout을 사용하게 되면, Network 출력에 dropout probablilty를 곱해줘야 함

• Dropout에 대해 요약하면,
  • Forward pass에 dropout을 추가하는 것은 간단함
    • 일부 노드를 무작위로 0으로 만들어 줌 (단 2줄)
  • Test time에서는 dropout probablilty를 곱해서 사용
• Dropout은 상당히 간단하게 적용시킬 수 있고, Neural Network의 regularization에 상당히 효과적임

• Dropout을 사용할 때, 고려할 수 있는 한 가지 트릭
  • Dropout을 역으로 계산하는 방법 (inverted dropout)
    • test time에서는 계산 효율이 중요하기 때문에, 곱하기 연산이 추가되는 것은 신경쓰이는 일임
    • 따라서, test time에서는 기존의 연산을 그대로 사용하고, train time에서 p를 나눠주는 방식을 사용

• Dropout은 일반적인 regularization 전략을 구체화 시킨 하나의 예시에 불과함
  • 이 전략은, train time에서 network에 무작위성(randomness)을 추가하여, training data에 너무 fit하지 않도록 함
    • 즉, network를 흩뜨려 놓음으로서, training data에 fit하는 것을 방해하는 것
  • test time에서는, randomness를 평균화 시켜서, generalization 효과를 주는 것
• Dropout이 regularization의 가장 대표적인 예이지만, Batch Normalization 또한 이와 비슷한 동작을 함
  • train time의 BN을 생각해보면, mini batch로 하나의 데이터가 샘플링 될 때, 매번 서로 다른 데이터들과 만남
    • train time에서는 각 데이터에 대해서, 이 데이터를 얼마나 어떻게 정규화시킬 것인지에 대한 stochasticity가 존재했음
  • 하지만, test time에서는 정규화를 mini batch 단위가 아닌, 전체 단위로 수행함으로서, stochasticality를 평균화 시킴
  • 이런 특성 때문에, BN은 dropout과 유사한 regularization 효과를 얻을 수 있음
• 실제로, BN을 사용할 때는, dropout을 사용하지 않음
  • BN도 충분히 regularization 효과가 있기 때문에

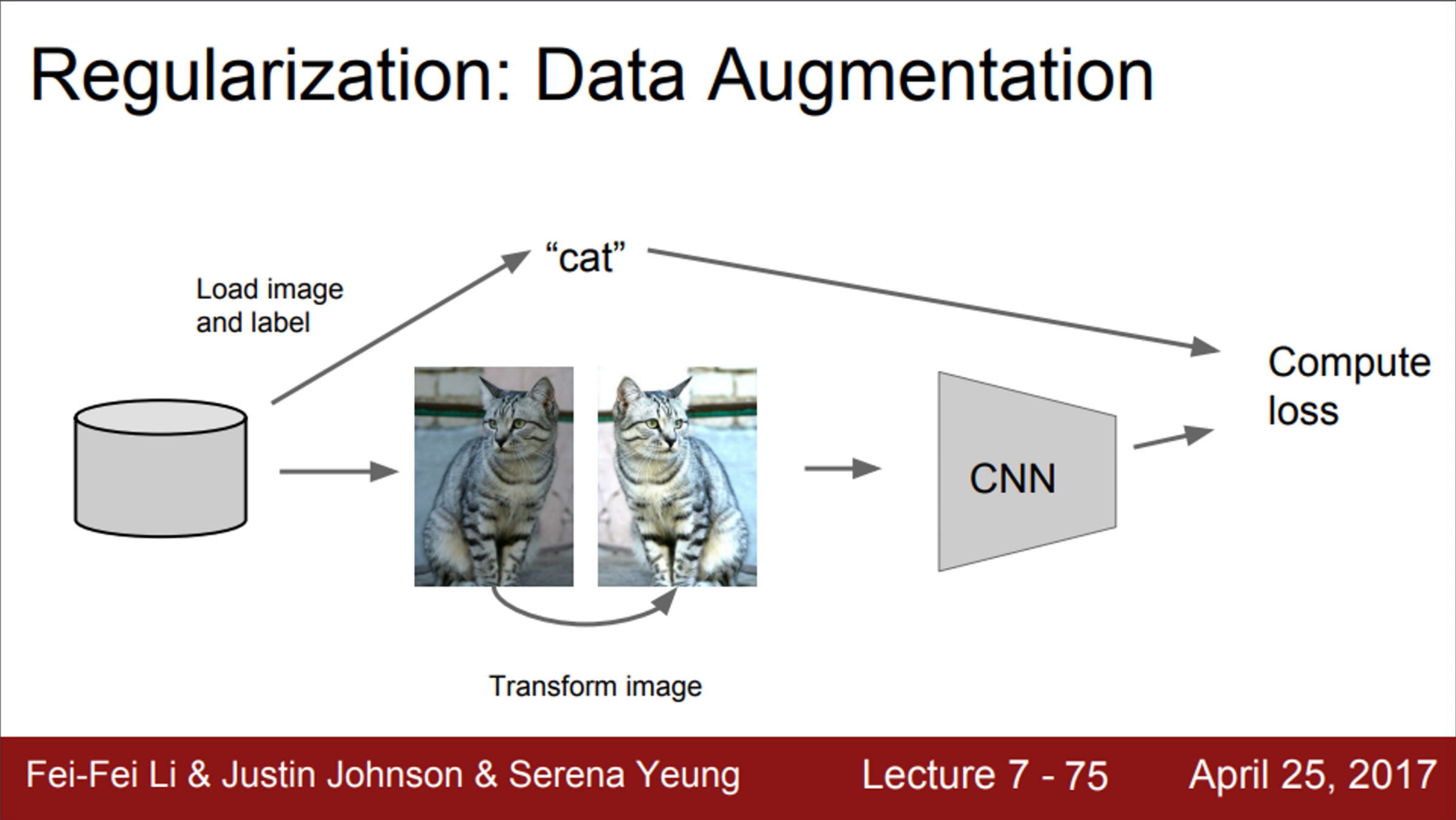
• Regularization의 또 다른 전략은, data augmentation
  • 기본 버전의 학습 과정에서는,
    • 데이터와 레이블이 있고, 이를 이용해서 매 step CNN을 업데이트 했음
  • data augmentation을 적용시킨 학습 과정에서는,
    • train time에서, 레이블은 그대로 놔둔 채, 이미지를 무작위로 변환시켜서 사용
    • 즉, 원본 이미지를 사용하는 것이 아닌, 무작위로 변환시킨 이미지로 학습시키게 되는 것임

• 위 예시는, 고양이 이미지를 horizontal filp 시킨 예시
  • 위 예시처럼, 이미지를 반전시켜도 고양이는 여전히 고양이

• 또, 이미지를 임의의 다양한 사이즈로 잘라서 사용할 수도 있음 (crop)
  • 그래도 고양이는 여전히 고양이
• Test time에서 stochasticity를 average out 시키는 것을 한번 고려해보면,
  • 4개의 각 코너와 중앙에서 잘라낸 이미지와, 이 이미지들의 반전 이미지를 사용
  • ImageNet 관련 논문들을 보면, 저자들이 보통 하나의 이미지를 그대로 사용했을 때 성능과 이미지 한장에서 10개를 잘라내서 성능을 비교함
    • 10 = (4개 코너 + 중앙) * (그냥 + 반전)

• Data augmentation에는 color jittering도 존재
  • 학습 시, 이미지의 contrast 또는 brightness를 바꿔줌
• color jittering에는 조금 더 복잡한 방법도 존재
  • PCA의 방향을 고려하여, color offset을 조절하는 방법
  • 이 방법은 color jittering을 data-dependent한 방법으로 진행하는 것
  • 자주 사용하는 방법은 아님

• 일반적으로, data augmentation은 어떤 문제에도 적용해 볼 수 있는 일반적인 방법
  • 어떤 문제를 풀려고 할 때, 이미지의 label을 바꾸지 않으면서, 이미지를 변환시킬 수 있는 많은 방법을 생각해 볼 수 있음
  • train time에서, 입력 데이터에 임의의 변환을 시켜주면, 일종의 regularization 효과를 얻을 수 있음

• 지금까지 Regularization의 세 가지 예시를 살펴봄
  • Dropout
  • Batch Normalization
  • Data Augmentation

• 추가적으로, Dropout과 유사한 방법이 하나 있음
  • DropConnect라는 방법
  • DropConnet는 activation이 아닌, weight matrix를 임의로 0으로 만드는 방법
  • Dropout과 동작도 비슷함

• 또 다른 방법은, Fractional Max Pooling
  • 사람들이 자주 쓰지는 않음
  • 보통 2X2 max pooling 연산은, 고정된 2X2 지역에서 수행함
  • 하지만, Fractional Max Pooling에서는 pooling 연산을 수행할 지역을 임의로 선정
  • test time에서, stochasticity를 average out 시키려면, pooling region을 고정시키거나, 혹은 여러 개의 pooling region을 만들고 average out 시킴

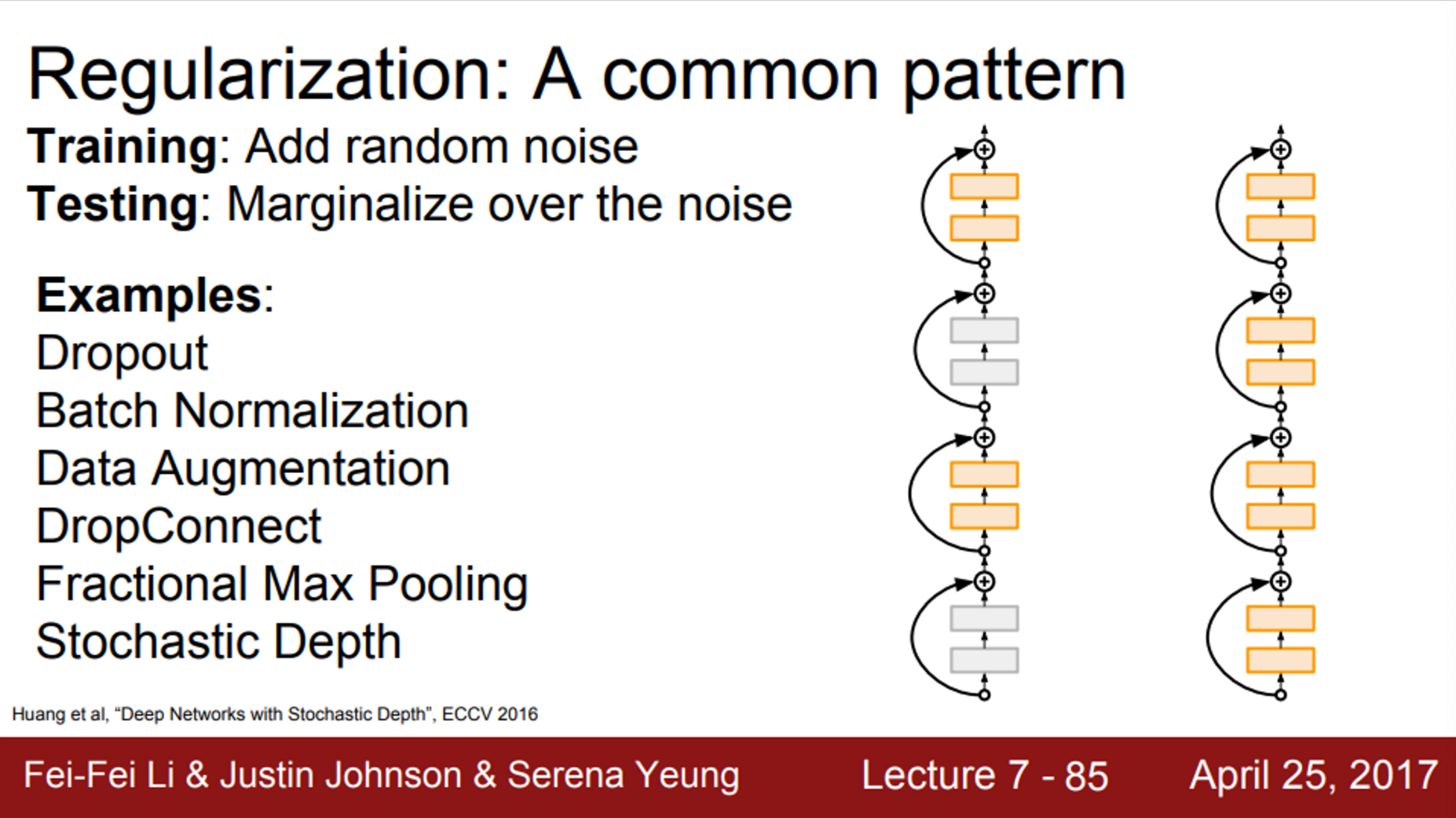
• 추가적으로, Stochastic Depth라는 방법도 존재
  • 깊은 network가 있을 때,
    • train time에서는 layer 중 일부를 제거하고, 일부만 사용해서 학습
    • test time에서는 전체 network를 다 사용
  • 이 방법의 regularization 효과는 dropout과 같은 다른 방법들과 유사

• 지금까지 regularization을 배움
  • 다양한 전략으로 train/test error 간의 격차를 줄이려는 시도
• overfitting이 일어날 수 있는 상황 중 하나는, 충분한 데이터가 없을 때
  • 작은 데이터셋에 지나치게 overfit할 수 있음
  • regularization을 통해서 이를 해결할 수 있지만, transfer learning이라는 방법도 존재

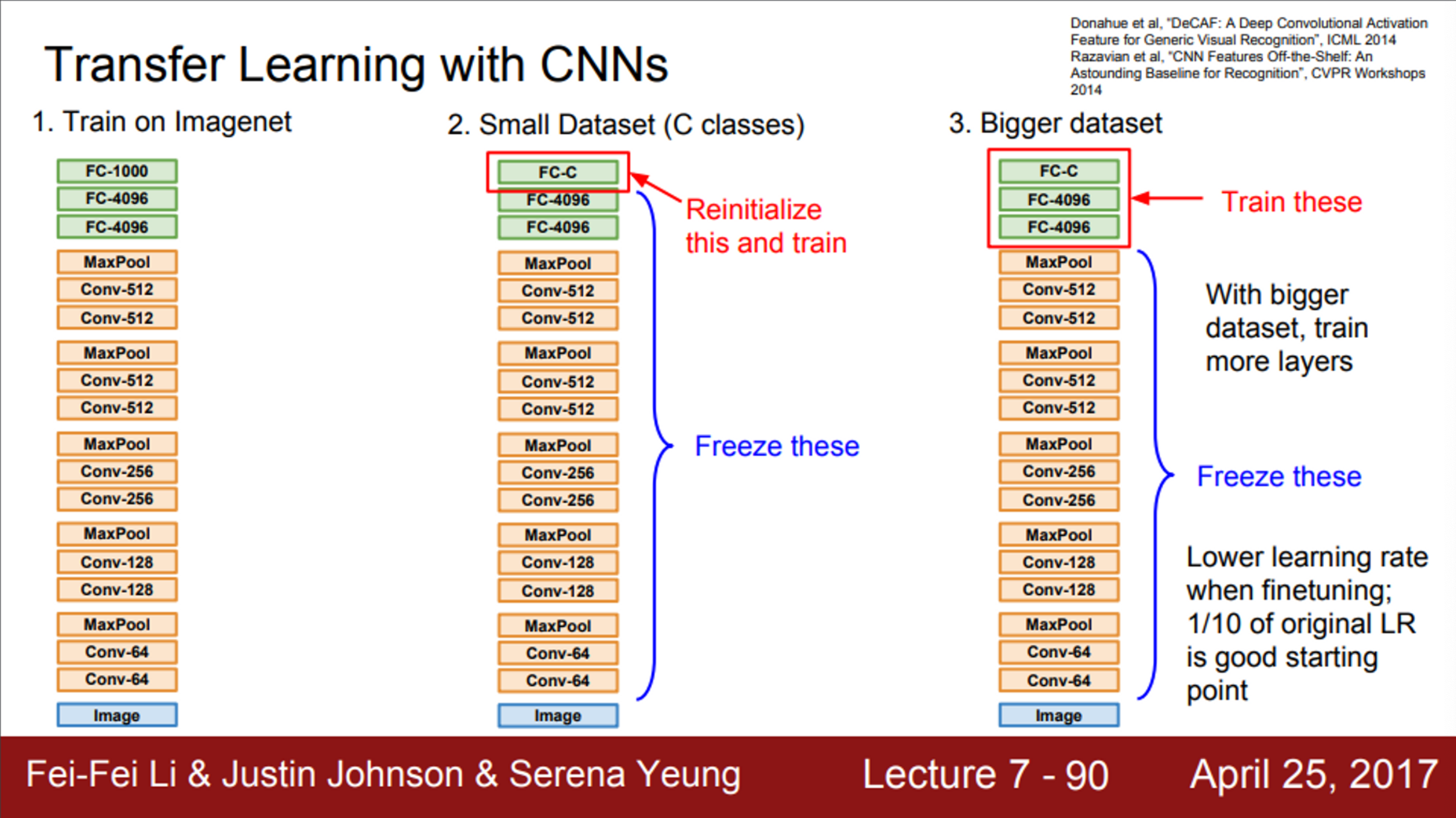
• 다음과 같은 CNN 모델이 있다고 가정
  • ImageNet 정도의 데이터셋이면, 전체 network를 학습시키기에는 충분한 양
  • 그 다음으로 할 일은, ImageNet에서 학습된 feature들을 우리가 가진 작은 데이터셋에 적용하는 것
    • 1000개의 ImageNet 카테고리를 분류하는 것이 아닌, 10종의 강아지를 분류하는 문제
    • 데이터는 엄청 적음
  • 일반적인 절차는, 가장 마지막의 FC layer를 초기화
    • 마지막 FC layer는 최종 feature와 class score 간의 연결
    • 기존 ImageNet을 학습시킬 때는 4096X1000 차원의 행렬이었음
    • 우리의 데이터셋에 적용시키기 위해서, 4096X10으로 바꿔줌
    • 그리고, 방금 정의한 가중치 행렬을 초기화시키고, 이전의 모든 layer들의 가중치는 freeze시킴
  • 이렇게 되면, linear classifier를 학습시키는 것과 같음
    • 오직 마지막 layer만 가지고, 우리의 데이터를 학습시키는 것
  • 이 방법을 사용하면, 아주 작은 데이터셋일지라도, 아주 잘 동작하는 모델을 만들 수 있음
• 만일 데이터가 조금 더 있다면, 전체 network를 fine-tuning을 할 수 있음
  • 최종 layer들을 학습시키고 나면, network의 일부만이 아닌 network 전체의 학습도 고려해 볼 수 있음
• 이 부분에서는 보통 기존의 learning rate보다는 낮춰서 학습 시킴
  • 기존의 가중치들이 ImageNet으로 잘 학습되어 있고, 이 가중치들이 잘 동작하기 때문
  • 우리가 가진 데이터셋에서의 성능을 높이기 위함이라면, 가중치들이 아주 조금씩만 수정되면 될 것임

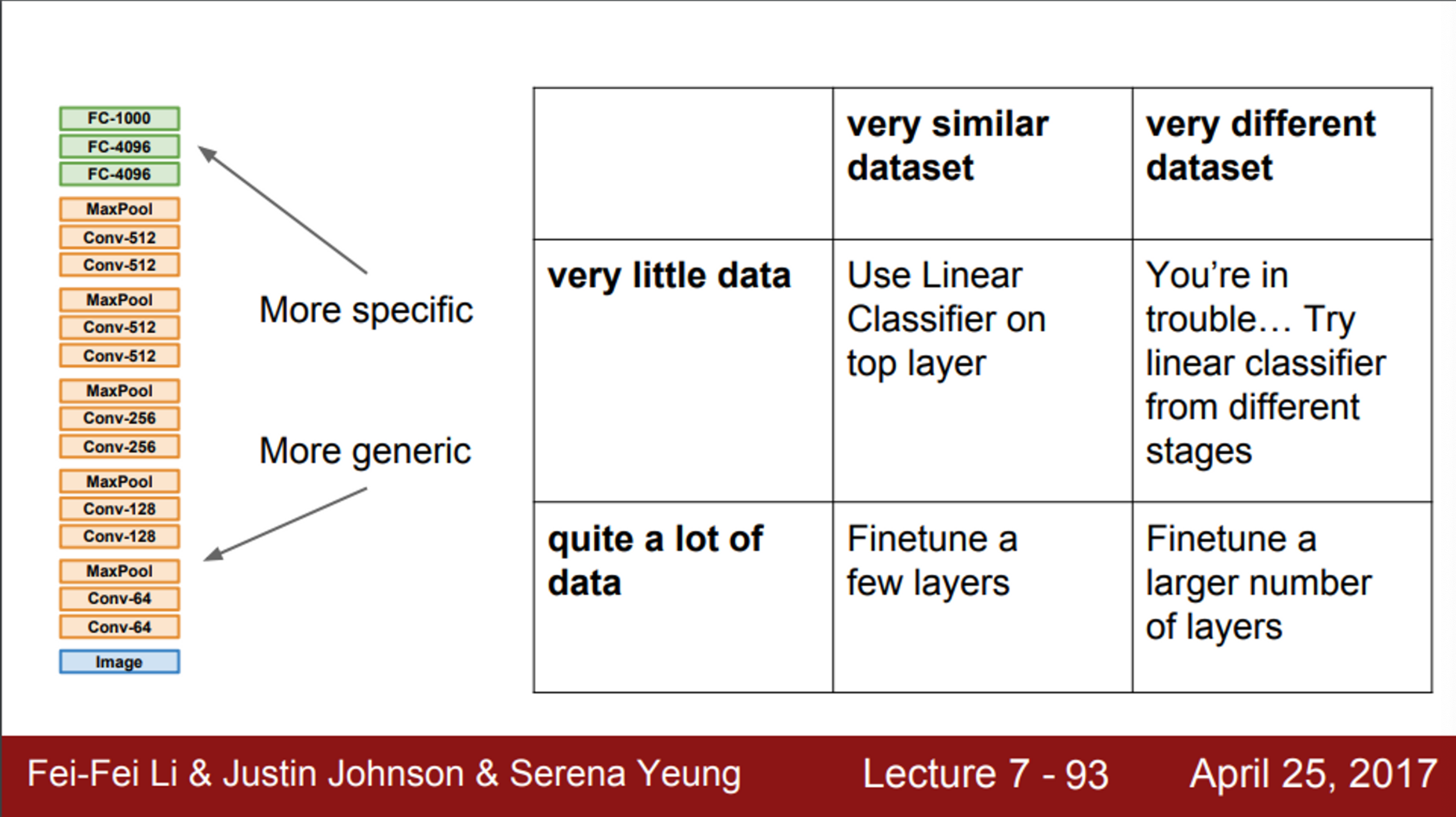
• 따라서, transfer learning을 수행 함에 있어서, 4가지 시나리오를 예상해 볼 수 있음
  • 적은 양의 데이터셋이 있고, 이전에 학습된 데이터셋과 현재 데이터셋이 유사한 경우
    • 기존 모델의 마지막 layer만 학습
  • 데이터가 조금 많고, 이전에 학습된 데이터셋과 현재 데이터셋이 유사한 경우
    • 모델 전체를 fine tuning
  • 적은 양의 데이터셋이 있고, 이전에 학습된 데이터셋과 현재 데이터셋이 다른 경우
    • 이런 경우는 문제가 될 수 있음
    • 마지막 layer만 학습시키는 것이 잘 동작할 수도 있지만, 쓸모없는 전략일 수도 있음
    • network의 더 많은 부분을 초기화시키거나, 다른 방법들을 고려해야함
  • 데이터가 조금 많고, 이전에 학습된 데이터셋과 현재 데이터셋이 유사한 경우
    • 이 경우에는, 더 많은 layer를 fine tuning

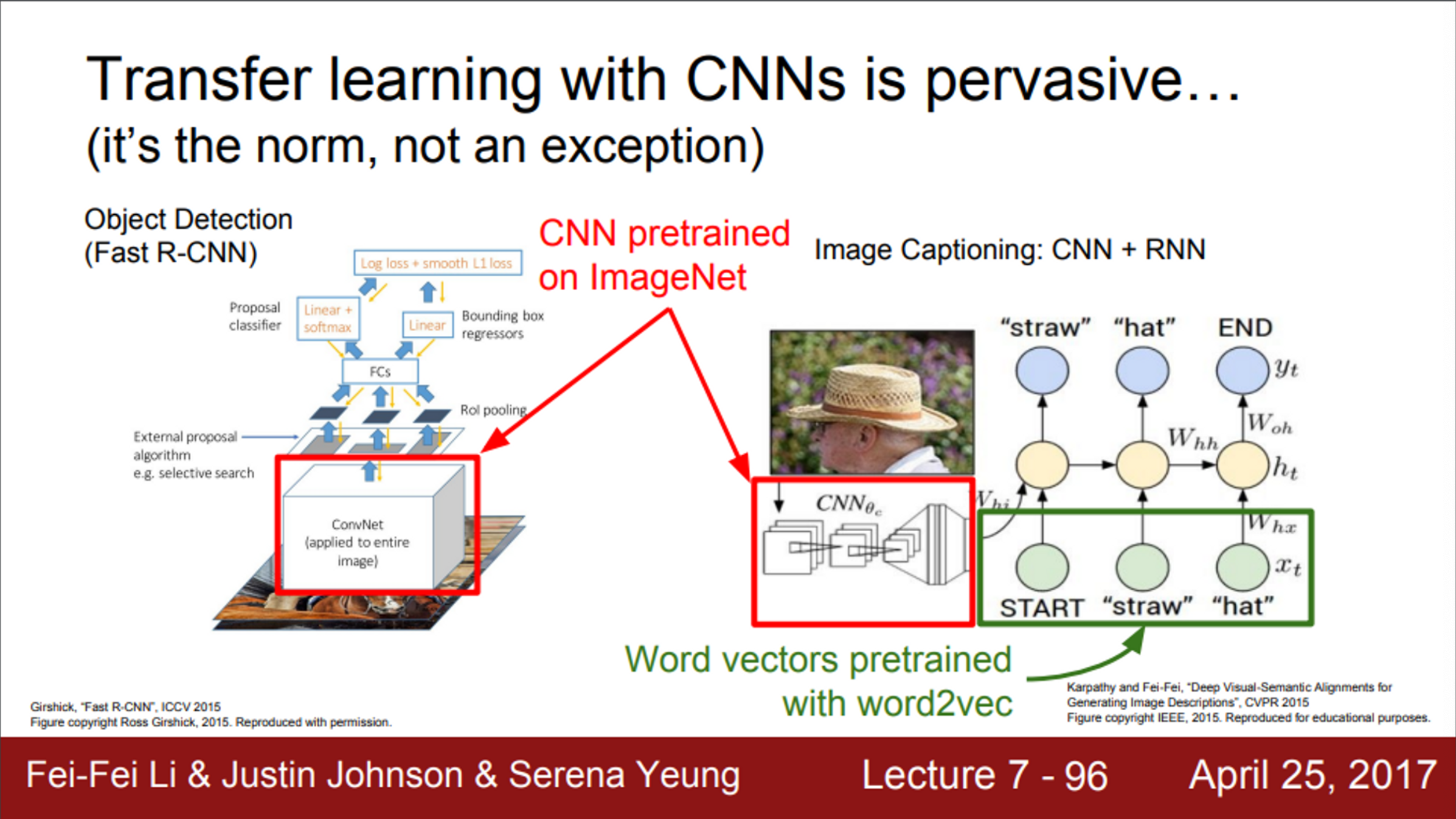
• transfer learning은 보편적임
  • 위 예시는, object detection(왼쪽), image captioning(오른쪽)
  • 두 모델 모두 CNN 구조를 가지고 있음
    • 기본적으로 이미지를 처리
    • 이 부분을 처음부터 학습시키지 않고, 대부분 ImageNet pretrained model을 사용하고, 현재 task에 맞도록 fine tuning 함