선입 선출 스케쥴링

문1) 처리해야 할 동일한 작업이 n 개가 있고, 이를 처리하기 위한 CPU가 있습니다.

이 CPU는 다음과 같은 특징이 있습니다.

• CPU에는 여러 개의 코어가 있고, 코어별로 한 작업을 처리하는 시간이 다릅니다.
• 한 코어에서 작업이 끝나면 작업이 없는 코어가 바로 다음 작업을 수행합니다.
• 2개 이상의 코어가 남을 경우 앞의 코어부터 작업을 처리 합니다.
  처리해야 될 작업의 개수 n과, 각 코어의 처리시간이 담긴 배열 cores 가 매개변수로 주어질 때, 마지막 작업을 처리하는 코어의 번호를 return 하는 solution 함수를 완성해주세요.

---

제한 사항

• 코어의 수는 10,000이하 2 이상 입니다.
• 코어당 작업을 처리하는 시간은 10,000이하 입니다.
• 처리해야 하는 일의 개수는 50,000개를 넘기지 않습니다.

---

입출력 예

n	cores	result
6	[1,2,3]	2

---

입출력 예 설명

입출력 예 #1

• 처음 3개의 작업은 각각 1,2,3번에 들어가고, 1시간 뒤 1번 코어에 4번째 작업,다시 1시간 뒤 1,2번 코어에 5,6번째 작업이 들어가므로 2를 반환해주면 됩니다.

---

나의 풀이

package programmers;

public class FIFOScheduling {

    public static int solution(int n, int[] cores) {
        int answer = 0;
        int coreCount = cores.length;
        
        if (n <= coreCount) return n;
    
        int start = 1;
        int end = cores[0] * n; 
        for (int core : cores) {
            end = Math.min(end, core * n);
        }
        int minTime = 0;
        int extraWork = 0; 
        
       
        while (start <= end) {
            int mid = (start + end) / 2;
            int work = calculateWork(mid, cores);
            
            if (work >= n) {
                end = mid - 1;
                minTime = mid;
                extraWork = work - n;
            } else {
                start = mid + 1;
            }
        }
        
        
        for (int i = coreCount - 1; i >= 0; i--) {
            if (minTime % cores[i] == 0) {
                if (extraWork == 0) {
                    answer = i + 1;
                    break;
                }
                extraWork--;
            }
        }
        
       
        return answer;
    }
    
    private static int calculateWork(int time, int[] cores) {
        int count = 0;
        for (int core : cores) {
            count += time / core + 1; 
        }
        return count;
    }

    public static void main(String[] args) {
        int[] cores = {1, 2, 3};
        solution(6, cores);
    }
}

---

나의 생각

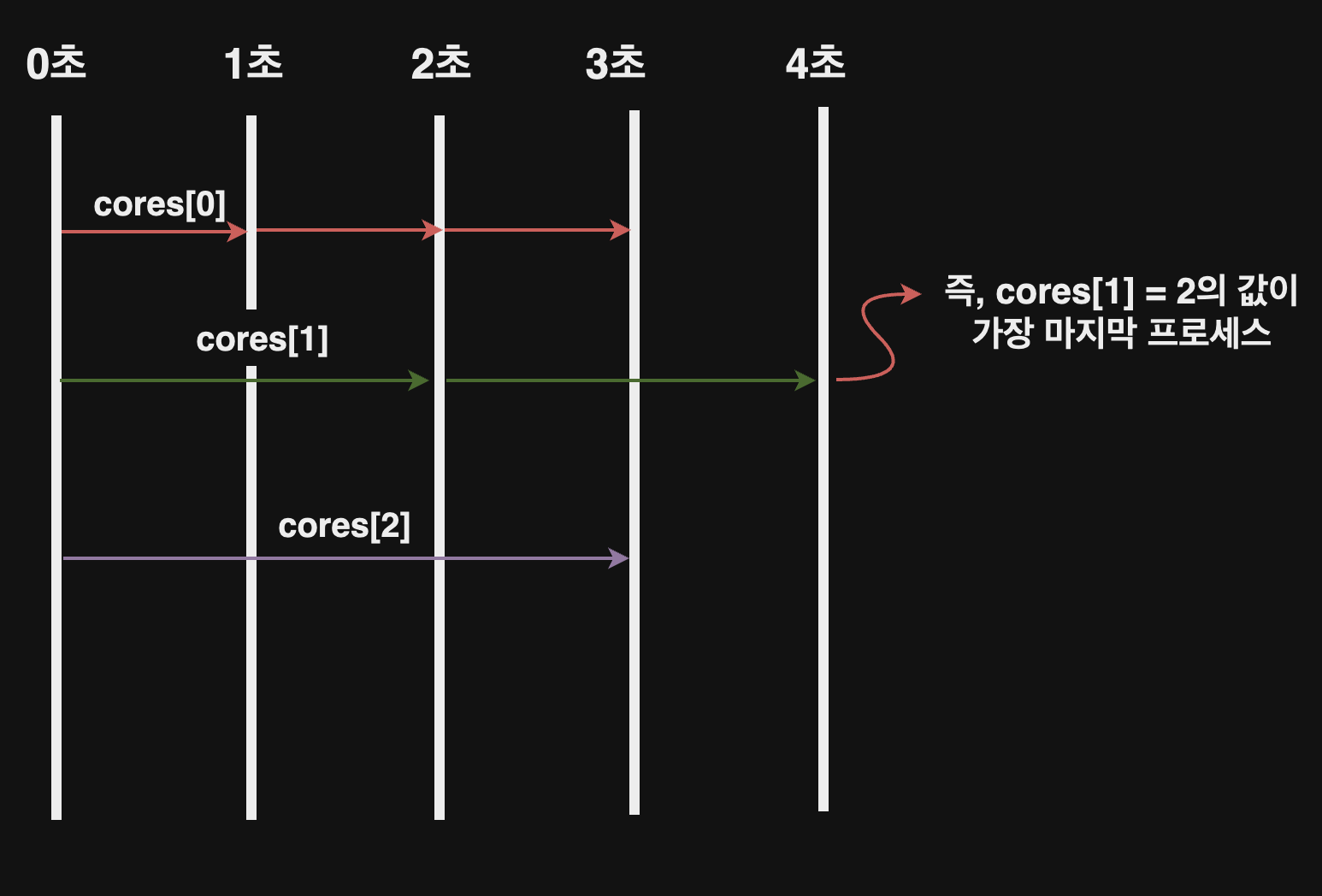
그림에 따르면, cores[0], cores[1], cores[2]가 순차적으로 작업을 처리하며, 빈 코어가 있을 때는 새로운 작업을 바로 할당받아 처리하는 FIFO(First IN First OUT) 스케쥴링의 개념을 나타내고 있다.

---

다단계 칫솔 판매

문2) 민호는 다단계 조직을 이용하여 칫솔을 판매하고 있습니다. 판매원이 칫솔을 판매하면 그 이익이 피라미드 조직을 타고 조금씩 분배되는 형태의 판매망입니다. 어느정도 판매가 이루어진 후, 조직을 운영하던 민호는 조직 내 누가 얼마만큼의 이득을 가져갔는지가 궁금해졌습니다. 예를 들어, 민호가 운영하고 있는 다단계 칫솔 판매 조직이 아래 그림과 같다고 합시다.

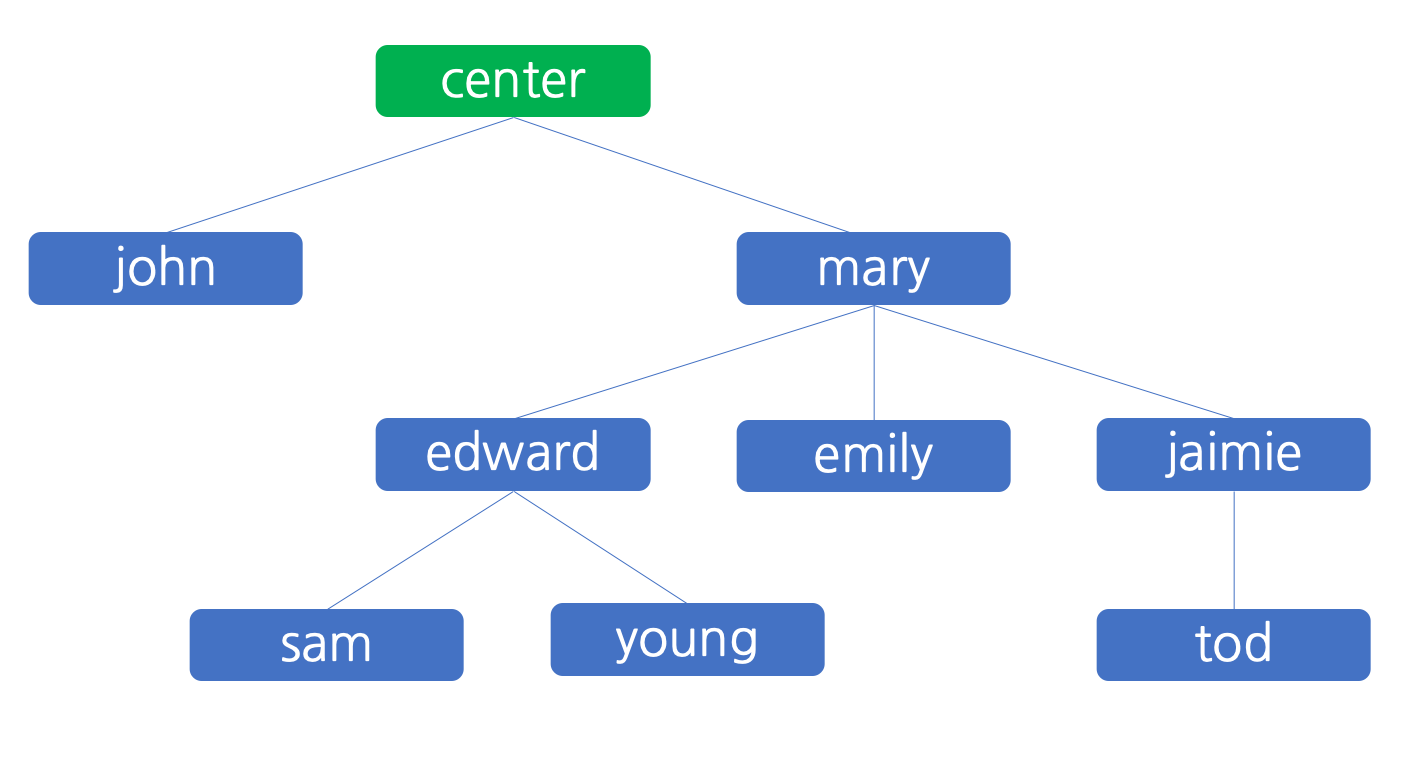
민호는 center이며, 파란색 네모는 여덟 명의 판매원을 표시한 것입니다. 각각은 자신을 조직에 참여시킨 추천인에 연결되어 피라미드 식의 구조를 이루고 있습니다. 조직의 이익 분배 규칙은 간단합니다. 모든 판매원은 칫솔의 판매에 의하여 발생하는 이익에서 10% 를 계산하여 자신을 조직에 참여시킨 추천인에게 배분하고 나머지는 자신이 가집니다. 모든 판매원은 자신이 칫솔 판매에서 발생한 이익 뿐만 아니라, 자신이 조직에 추천하여 가입시킨 판매원에게서 발생하는 이익의 10% 까지 자신에 이익이 됩니다. 자신에게 발생하는 이익 또한 마찬가지의 규칙으로 자신의 추천인에게 분배됩니다. 단, 10% 를 계산할 때에는 원 단위에서 절사하며, 10%를 계산한 금액이 1 원 미만인 경우에는 이득을 분배하지 않고 자신이 모두 가집니다.

예를 들어, 아래와 같은 판매 기록이 있다고 가정하겠습니다. 칫솔의 판매에서 발생하는 이익은 개당 100 원으로 정해져 있습니다.

판매원	판매 수량	이익금
young	12	1,200원
john	4	400원
tod	2	200원
emily	5	500원
mary	10	1,000원

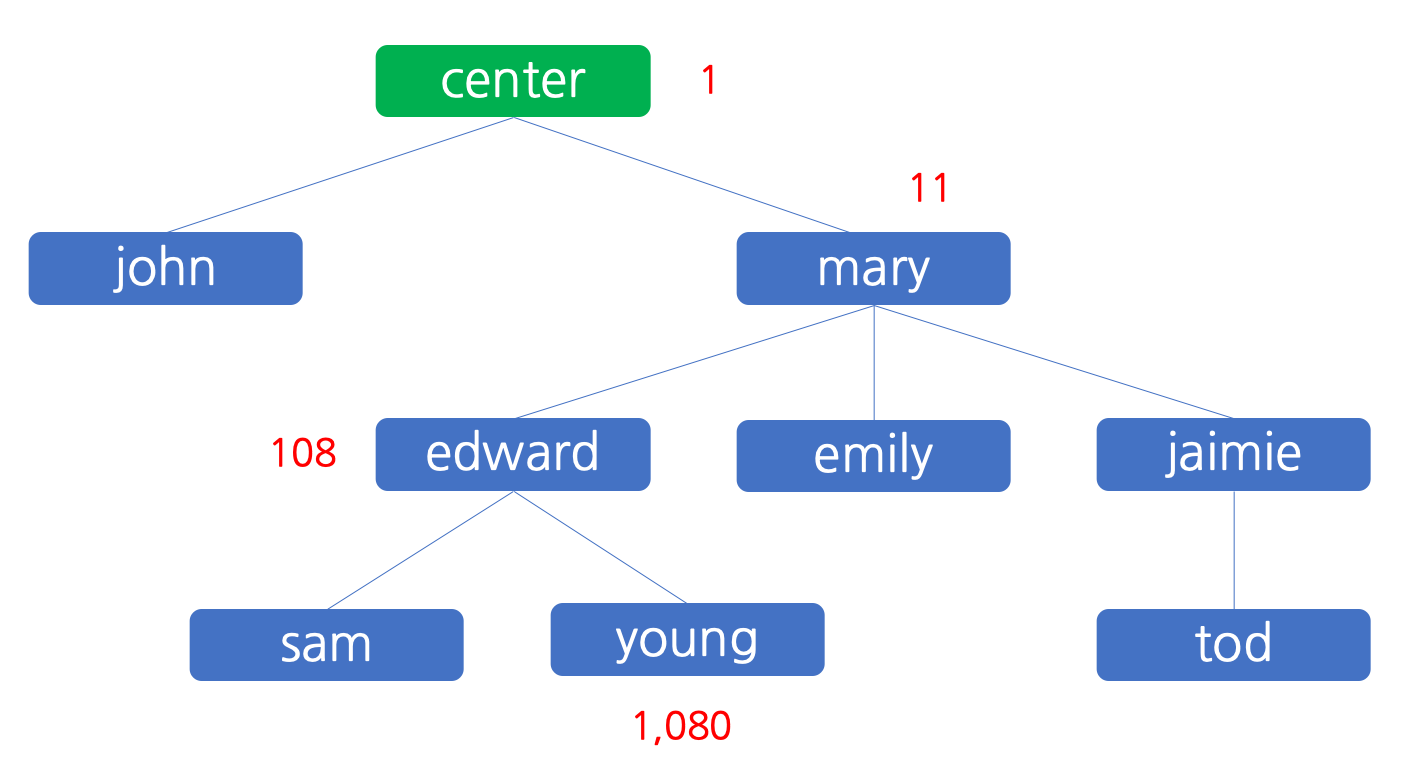
그 후, 판매원 john 에 의하여 400 원의 이익이 발생합니다. john 은 10% 인 40 원을 센터에 배분하고 자신이 나머지인 360 원을 가집니다. 이 상태를 그림으로 나타내면 아래와 같습니다.

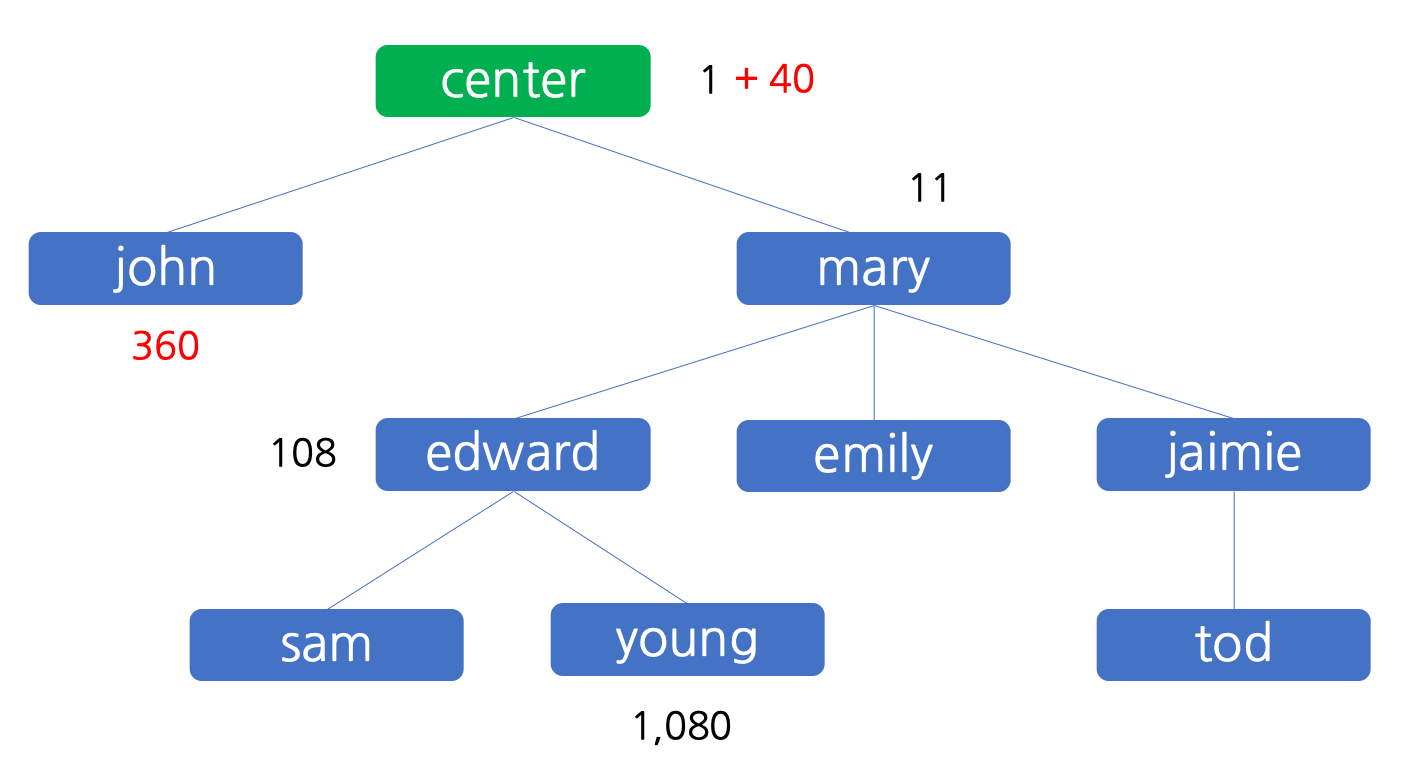
또 그 후에는 판매원 tod 에 의하여 200 원 이익이 발생하는데, tod 자신이 180 원을, 추천인인 jaimie 가 그 중 10% 인 20 원을 받아서 18 원을 가지고, jaimie 의 추천인인 mary 는 2 원을 받지만 이것의 10% 는 원 단위에서 절사하면 배분할 금액이 없기 때문에 mary 는 2 원을 모두 가집니다. 이 상태를 그림으로 나타내면 아래와 같습니다.

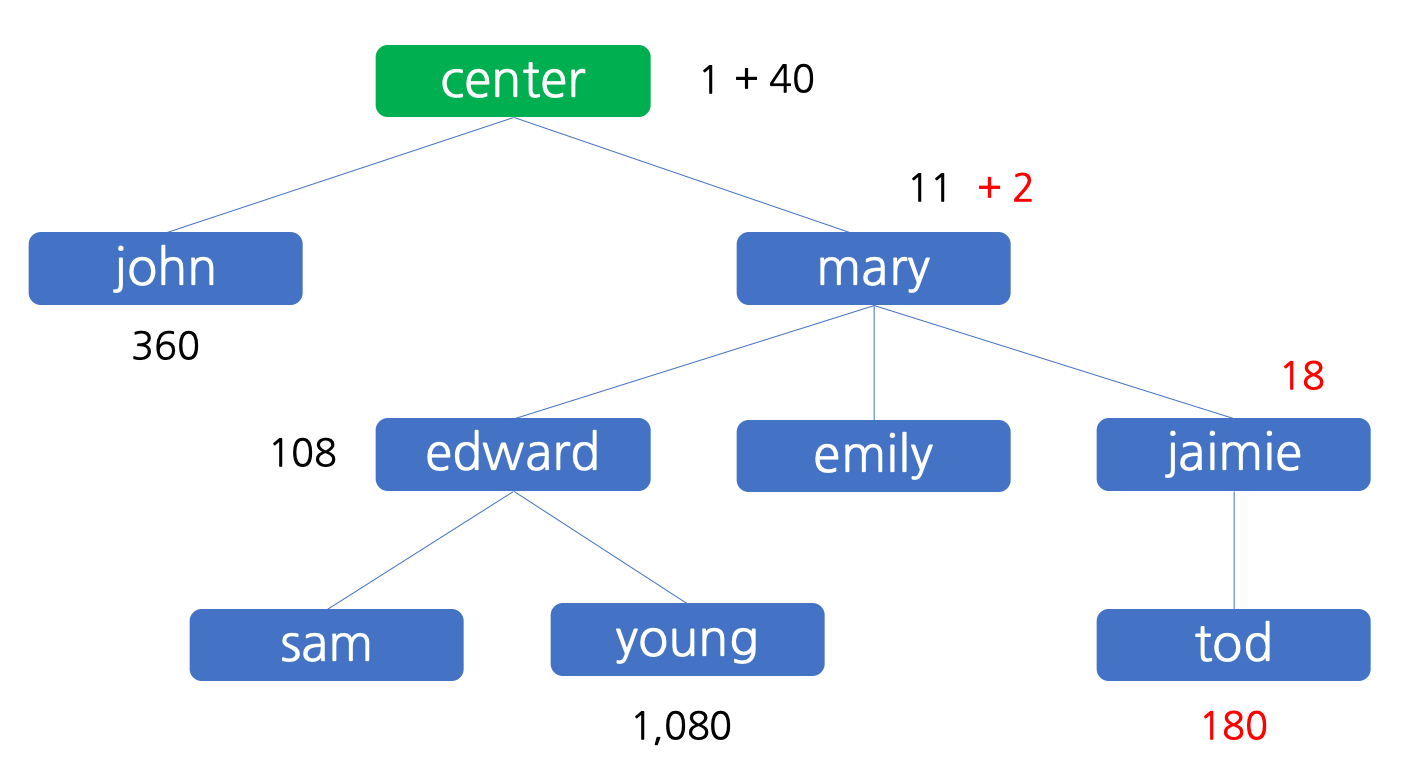
그 다음으로 emily 가 칫솔 판매를 통하여 얻은 이익 500 원은 마찬가지의 규칙에 따라 emily 에게 450 원, mary 에게 45 원, 그리고 센터에 5 원으로 분배됩니다. 이 상태를 그림으로 나타내면 아래와 같습니다.

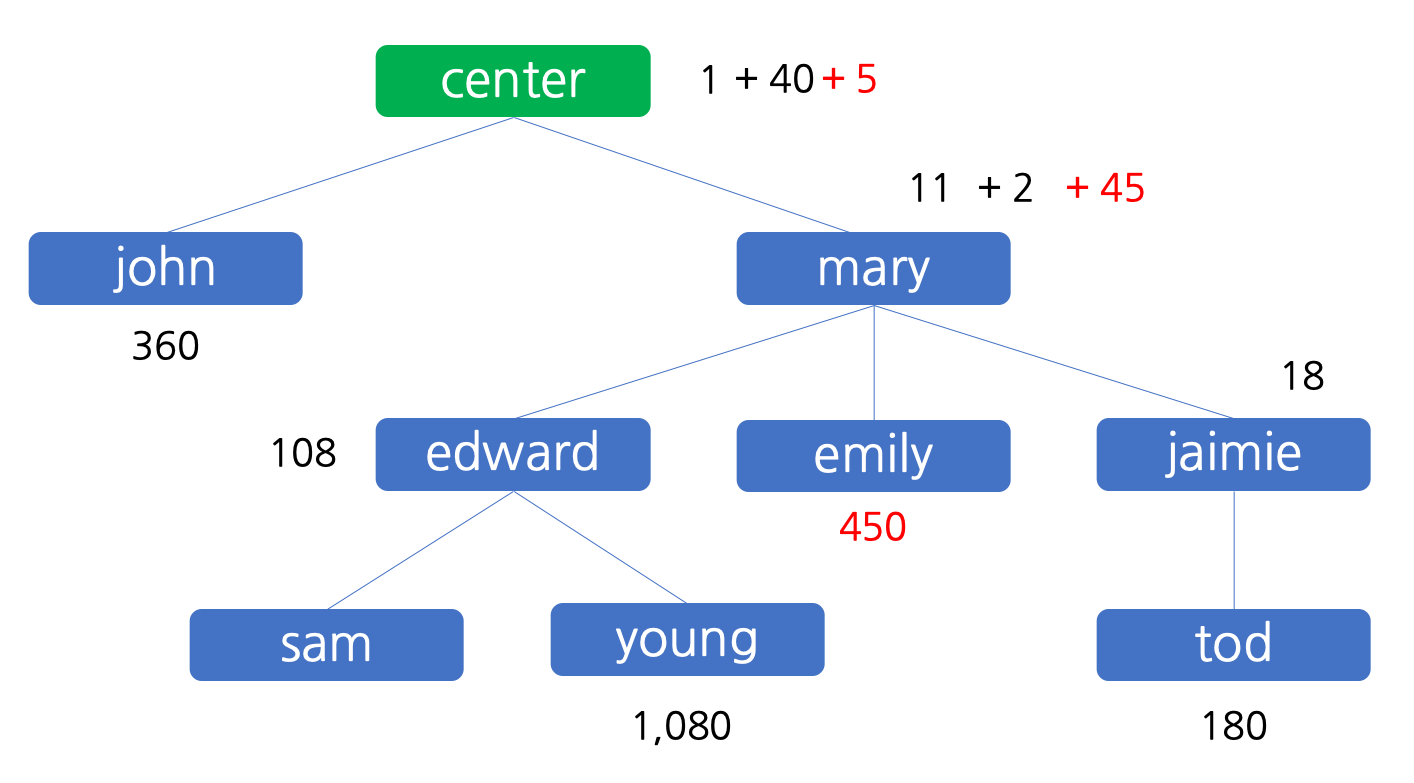
마지막으로, 판매원 mary 는 1,000 원의 이익을 달성하고, 이 중 10% 인 100 원을 센터에 배분한 후 그 나머지인 900 원을 자신이 가집니다. 이 상태를 그림으로 나타내면 아래와 같습니다.

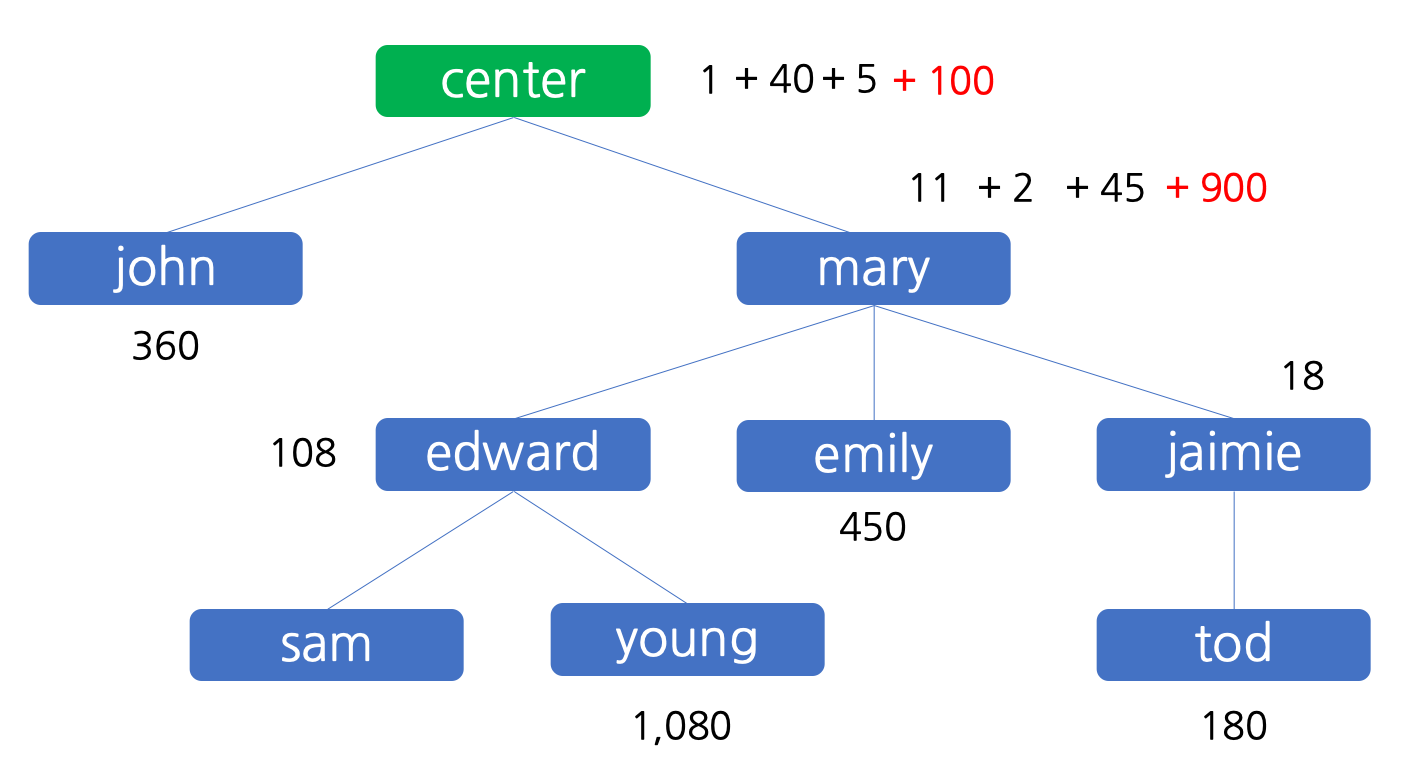
위와 같이 하여 모든 조직 구성원들의 이익 달성 현황 집계가 끝났습니다. 지금까지 얻은 이익을 모두 합한 결과를 그림으로 나타내면 아래와 같습니다.

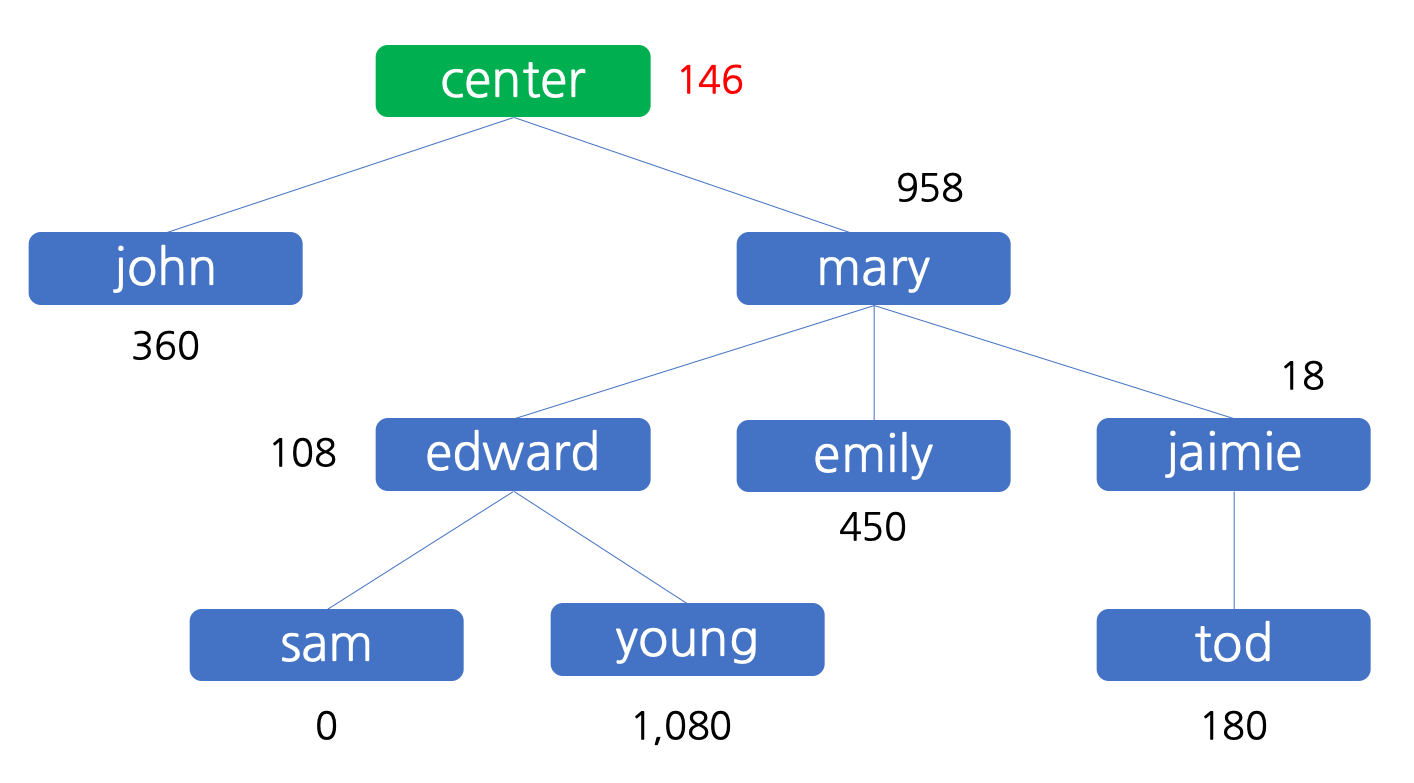
이 결과가 민호가 파악하고자 하는 이익 배분 현황입니다.

각 판매원의 이름을 담은 배열 enroll, 각 판매원을 다단계 조직에 참여시킨 다른 판매원의 이름을 담은 배열 referral, 판매량 집계 데이터의 판매원 이름을 나열한 배열 seller, 판매량 집계 데이터의 판매 수량을 나열한 배열 amount가 매개변수로 주어질 때, 각 판매원이 득한 이익금을 나열한 배열을 return 하도록 solution 함수를 완성해주세요. 판매원에게 배분된 이익금의 총합을 계산하여(정수형으로), 입력으로 주어진 enroll에 이름이 포함된 순서에 따라 나열하면 됩니다.

---

제한사항

• enroll의 길이는 1 이상 10,000 이하입니다.
  • enroll에 민호의 이름은 없습니다. 따라서 enroll의 길이는 민호를 제외한 조직 구성원의 총 수입니다.
• referral의 길이는 enroll의 길이와 같습니다.
  • referral 내에서 i 번째에 있는 이름은 배열 enroll 내에서 i 번째에 있는 판매원을 조직에 참여시킨 사람의 이름입니다.
  • 어느 누구의 추천도 없이 조직에 참여한 사람에 대해서는 referral 배열 내에 추천인의 이름이 기입되지 않고 “-“ 가 기입됩니다. 위 예제에서는 john 과 mary 가 이러한 예에 해당합니다.
  • enroll 에 등장하는 이름은 조직에 참여한 순서에 따릅니다.
  • 즉, 어느 판매원의 이름이 enroll 의 i 번째에 등장한다면, 이 판매원을 조직에 참여시킨 사람의 이름, 즉 referral 의 i 번째 원소는 이미 배열 enroll 의 j 번째 (j < i) 에 등장했음이 보장됩니다.
• seller의 길이는 1 이상 100,000 이하입니다.
  • seller 내의 i 번째에 있는 이름은 i 번째 판매 집계 데이터가 어느 판매원에 의한 것인지를 나타냅니다.
  • seller 에는 같은 이름이 중복해서 들어있을 수 있습니다.
• amount의 길이는 seller의 길이와 같습니다.
  • amount 내의 i 번째에 있는 수는 i 번째 판매 집계 데이터의 판매량을 나타냅니다.
  • 판매량의 범위, 즉 amount 의 원소들의 범위는 1 이상 100 이하인 자연수입니다.
• 칫솔 한 개를 판매하여 얻어지는 이익은 100 원으로 정해져 있습니다.
• 모든 조직 구성원들의 이름은 10 글자 이내의 영문 알파벳 소문자들로만 이루어져 있습니다.

---

입출력 예

enroll	referral	seller	amount	result
["john", "mary", "edward", "sam", "emily", "jaimie", "tod", "young"]	["-", "-", "mary", "edward", "mary", "mary", "jaimie", "edward"]	["young", "john", "tod", "emily", "mary"]	[12, 4, 2, 5, 10]	[360, 958, 108, 0, 450, 18, 180, 1080]
["john", "mary", "edward", "sam", "emily", "jaimie", "tod", "young"]	["-", "-", "mary", "edward", "mary", "mary", "jaimie", "edward"]	["sam", "emily", "jaimie", "edward"]	[2, 3, 5, 4]	[0, 110, 378, 180, 270, 450, 0, 0]

---

나의 풀이

package programmers;

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;

public class Multistep {
	
	public static int[] solution(String[] enroll, String[] referral, String[] seller, int[] amount) {
       
        Map<String, Integer> profitMap = new HashMap<>();
        Map<String, String> referralMap = new HashMap<>();
        
        
        for (int i = 0; i < enroll.length; i++) {
            profitMap.put(enroll[i], 0); 
            referralMap.put(enroll[i], referral[i]);
        }
        
        for(int i = 0; i < seller.length; i++) {
        	String currentSeller = seller[i];
        	int currentProfit = amount[i] * 100;
        	
        	while (!currentSeller.equals("-") && currentProfit > 0) {
        		int distribution = currentProfit / 10;
        		System.out.println(distribution);
        		if (distribution < 1) {
    		        profitMap.put(currentSeller, profitMap.get(currentSeller) + currentProfit);
    		        break;
        		}
        		int remainingProfit = currentProfit - distribution;
        		
        		
        		profitMap.put(currentSeller, profitMap.get(currentSeller) + remainingProfit );
        		currentSeller = referralMap.get(currentSeller);
        		currentProfit = distribution;
        	}
        }
        
        int[] answer = new int[enroll.length];
        for (int i = 0; i < enroll.length; i++) {
            answer[i] = profitMap.get(enroll[i]);
        }
        System.out.println(Arrays.toString(answer));
        return answer;
    }
	
	public static void main(String[] args) {
		
		String[] enroll = {"john", "mary", "edward", "sam", "emily", "jaimie", "tod", "young"};
		String[] referral = {"-", "-", "mary", "edward", "mary", "mary", "jaimie", "edward"};
		String[] seller = {"young", "john", "tod", "emily", "mary"};
		int[] amount = {12, 4, 2, 5, 10};
		
		
		solution(enroll, referral, seller, amount);
	}

}

---

나의 생각

언뜻 문제를 보면 무척 복잡해 보이지만, 접근법은 다른 알고리즘 문제보다 명확했다. 문제의 핵심은 판매원이 득한 이익금은 얼마인가? 인데, String[] enroll, referral 은 key, value 형태의 map으로 이를 표현하면 되겠다고 생각했다.

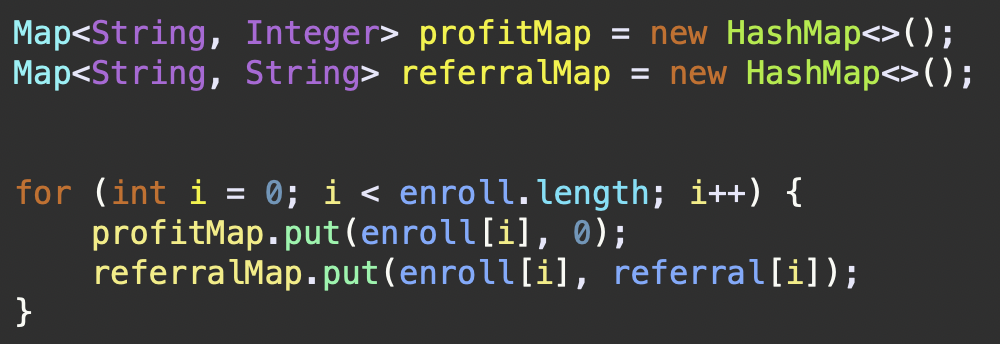
판매원의 이름과 이익금을 담고 있는 profitMap과 판매원의 이름과 그를 추천한 추천인이 담긴 referralmap을 먼저 선언하고 이를 for문 순회를 통해 데이터를 담았다.

내가 이 문제를 보며 생각했던 방법은 다음과 같다.

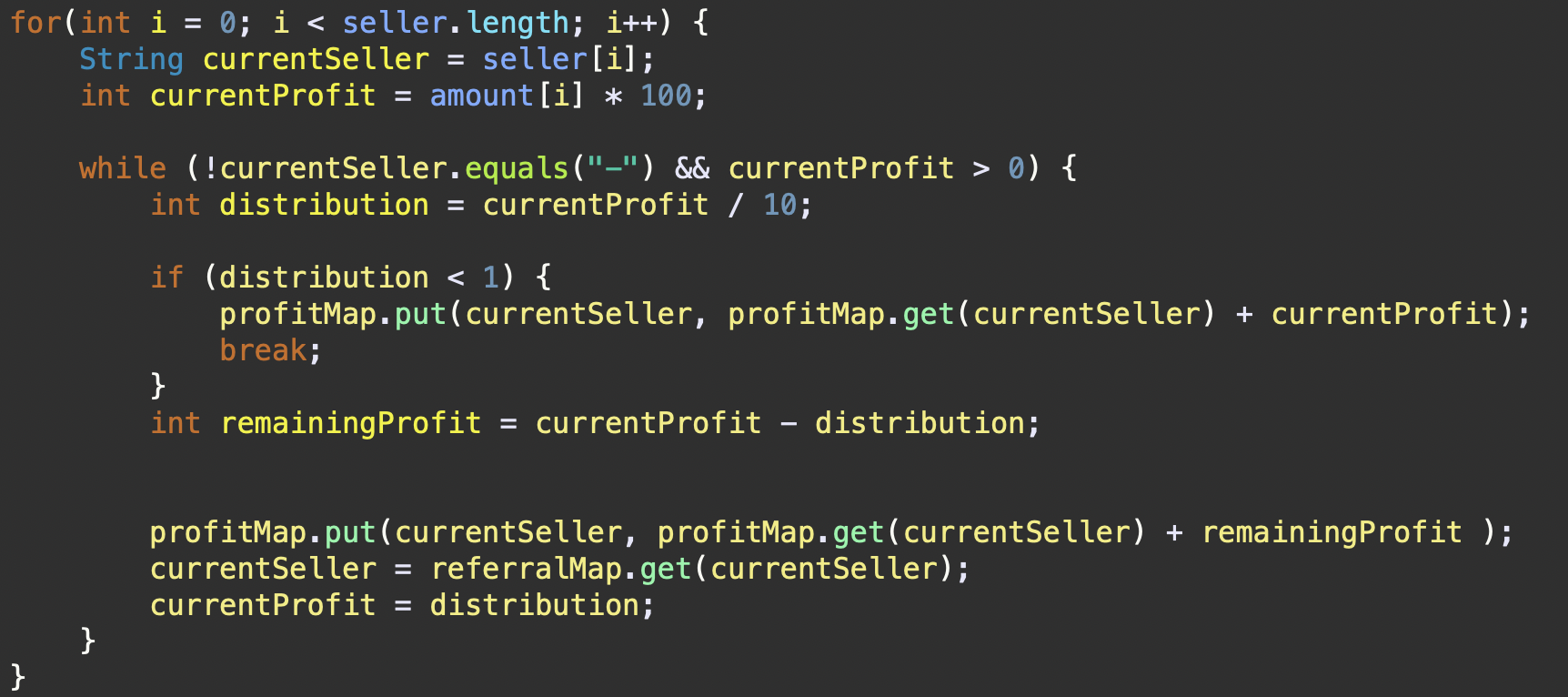
만약, seller 배열에서 young을 먼저 보면

• young의 판매금을 계산한다. → amount(12) * pricePerPiece(개당가격 100원)
  • 판매금의 10%에 해당하는 금액을 추천인에게 분배 → 판매금 / 10
  • 판매금에서 분배금을 뺀 금액을 young한테 전달
  • 현재 seller는 young의 추천인 edward
  • 현재 수익은 분배금으로 설정
  • 단, distribution이 1보다 작으면 분배 과정을 중지
• 이를 정리하면,
  profitMap에서 각 seller의 이익을 확인한 후, referralMap을 통해 해당 seller의 추천인을 찾는다. 이 추천인이 profitMap에 존재하는 경우, 그 추천인의 이익을 업데이트한다. 이 추천인을 referralMap의 key로 간주하고, referralMap에서 이 key에 대응하는 value(추천인의 추천인)를 찾아 profitMap에서 이를 다시 검색하는 과정을 반복한다. 이 과정은 추천인이 더 이상 없거나("-"에 도달하거나), 수익이 0보다 클 때까지 계속된다. 이렇게 해서, 포인터가 다음 노드를 가리키는 것처럼, 각 판매원의 추천 체인을 따라가며 수익 분배를 실행하고, 최종적으로 판매 네트워크의 뿌리인 "-"에 도달하여 전체 과정을 완료한다.

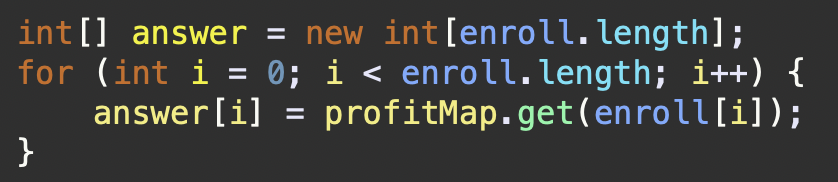
최종적으로 문제에서 반환해야하는 값은 enroll 배열에 등록된 순서대로 얼마의 수익을 얻는가?가 핵심이기 때문에 profitMap에서 enroll에 등록된 순서대로 값(value)를 answer[i]에 넣으면 된다.

---

파괴되지 않은 건물

문3) N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.

적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.

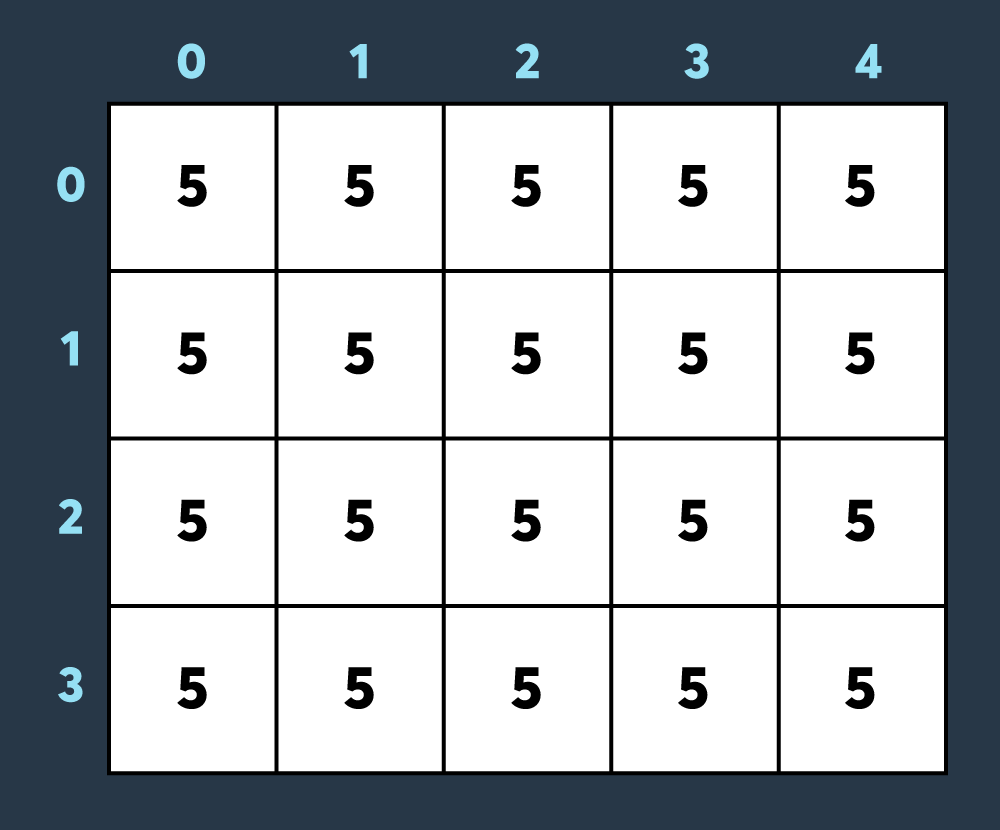
첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

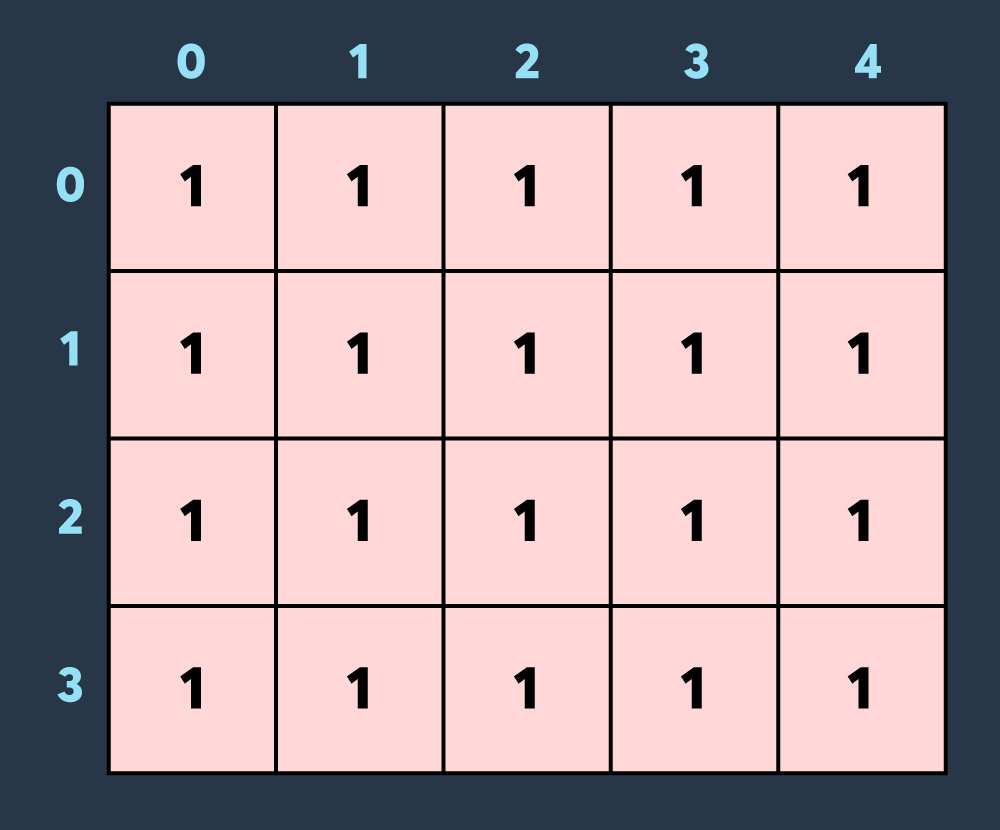
두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.

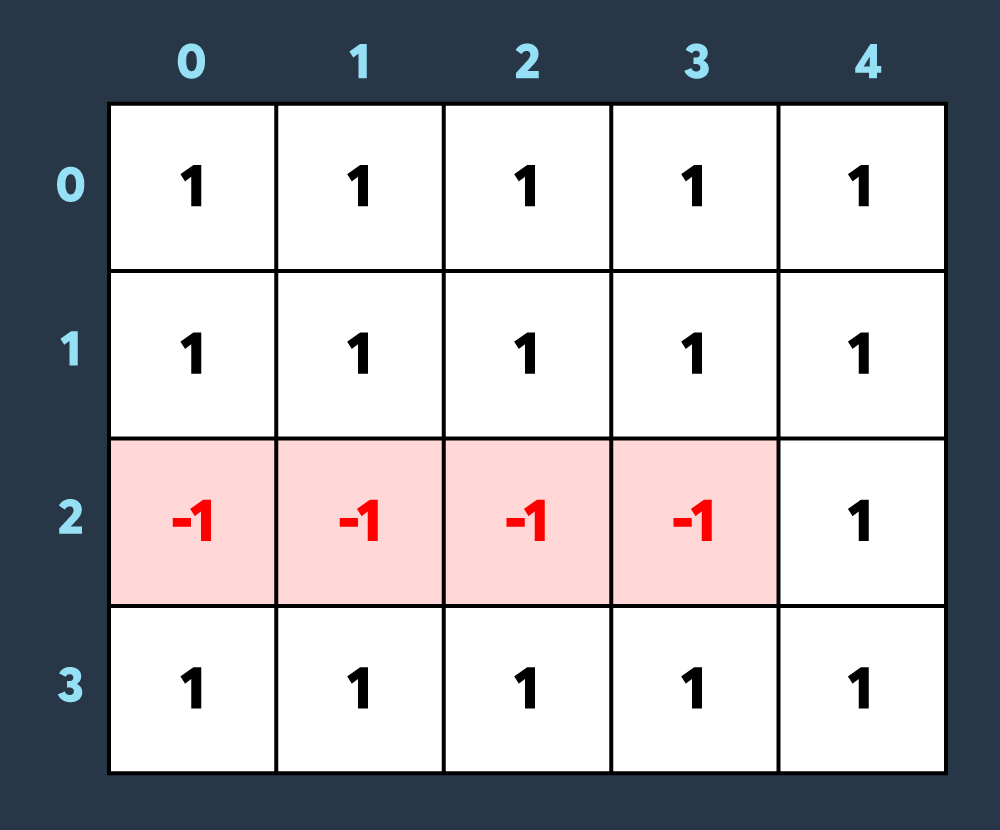
세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.

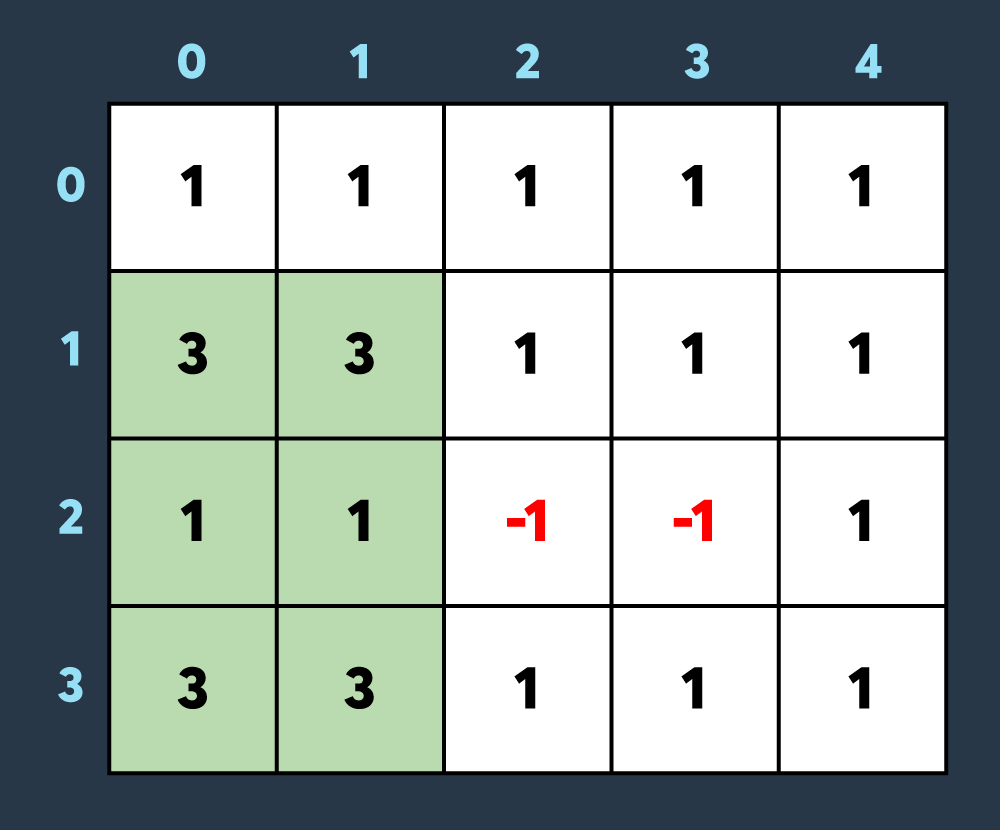
마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)

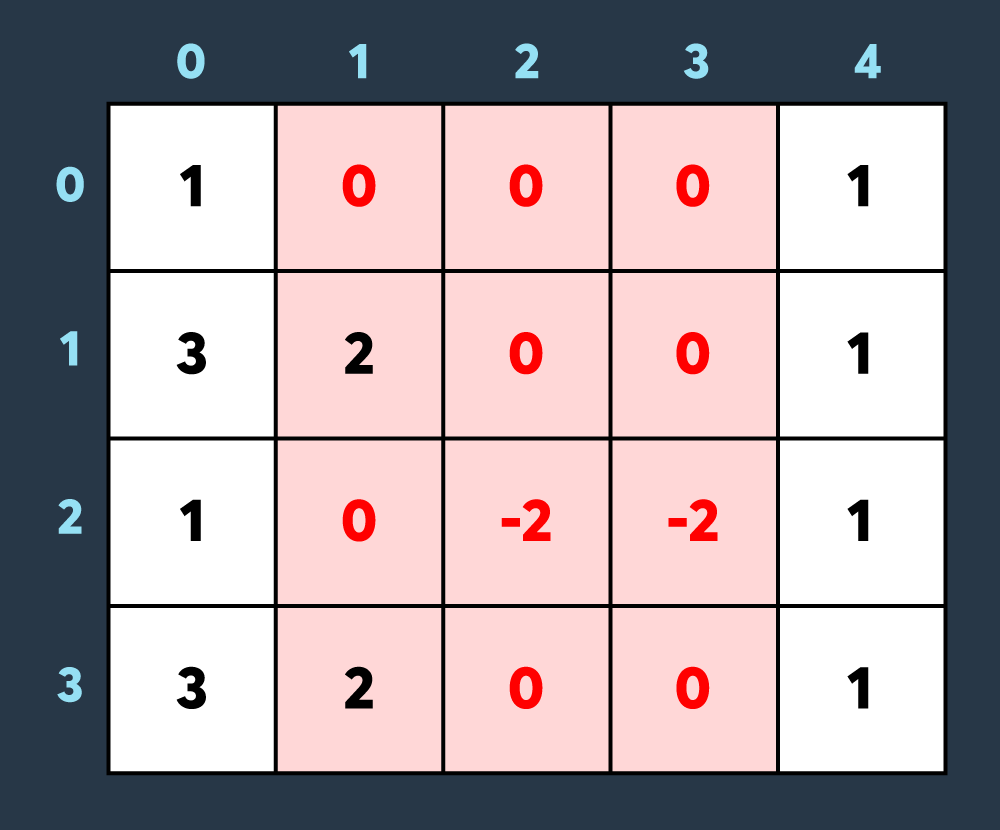
최종적으로 총 10개의 건물이 파괴되지 않았습니다.

건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.

---

제한 사항

• 1 ≤ board의 행의 길이 (= N) ≤ 1,000
• 1 ≤ board의 열의 길이 (= M) ≤ 1,000
• 1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
• 1 ≤ skill의 행의 길이 ≤ 250,000
• skill의 열의 길이 = 6
• skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
  • type은 1 혹은 2입니다.
    • type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
    • type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
  • (r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
    • 0 ≤ r1 ≤ r2 < board의 행의 길이
    • 0 ≤ c1 ≤ c2 < board의 열의 길이
    • 1 ≤ degree ≤ 500
    • type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
    • type이 2이면 degree만큼 건물의 내구도를 높입니다.
• 건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.

정확성 테스트 케이스 제한 사항

• 1 ≤ board의 행의 길이 (= N) ≤ 100
• 1 ≤ board의 열의 길이 (= M) ≤ 100
• 1 ≤ board의 원소 (각 건물의 내구도) ≤ 100
• 1 ≤ skill의 행의 길이 ≤ 100
  • 1 ≤ degree ≤ 100

---

입출력 예

board	skill	result
[[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5]]	[[1,0,0,3,4,4],[1,2,0,2,3,2],[2,1,0,3,1,2],[1,0,1,3,3,1]]	10
[[1,2,3],[4,5,6],[7,8,9]]	[[1,1,1,2,2,4],[1,0,0,1,1,2],[2,2,0,2,0,100]]	6

---

입출력 예 설명

입출력 예 #2

<초기 맵 상태>

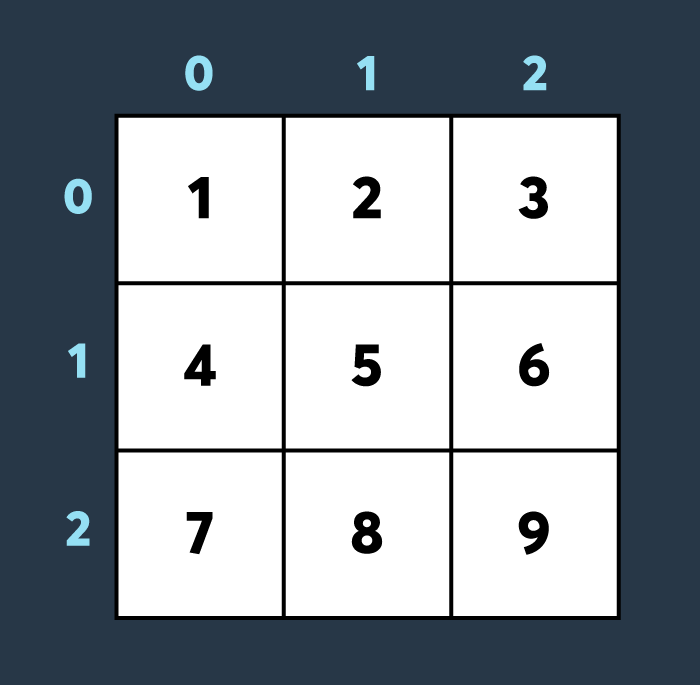
첫 번째로 적이 맵의 (1,1)부터 (2,2)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

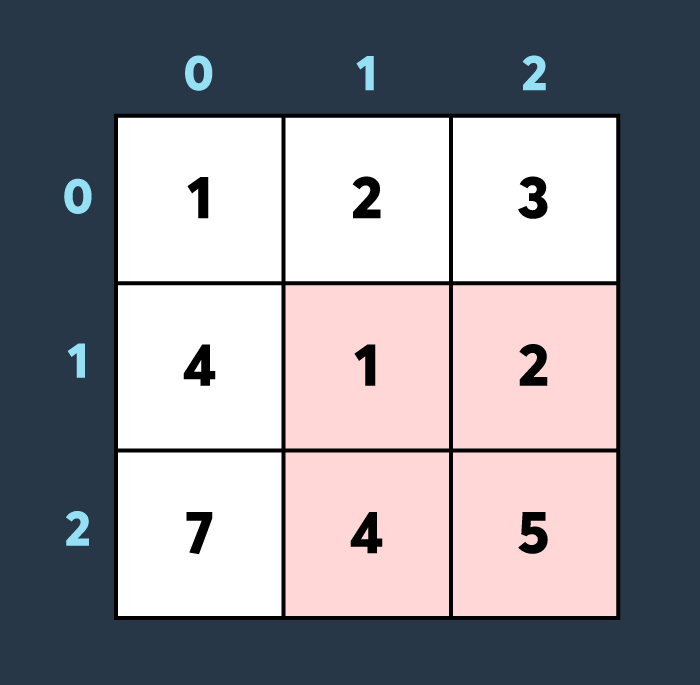
두 번째로 적이 맵의 (0,0)부터 (1,1)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

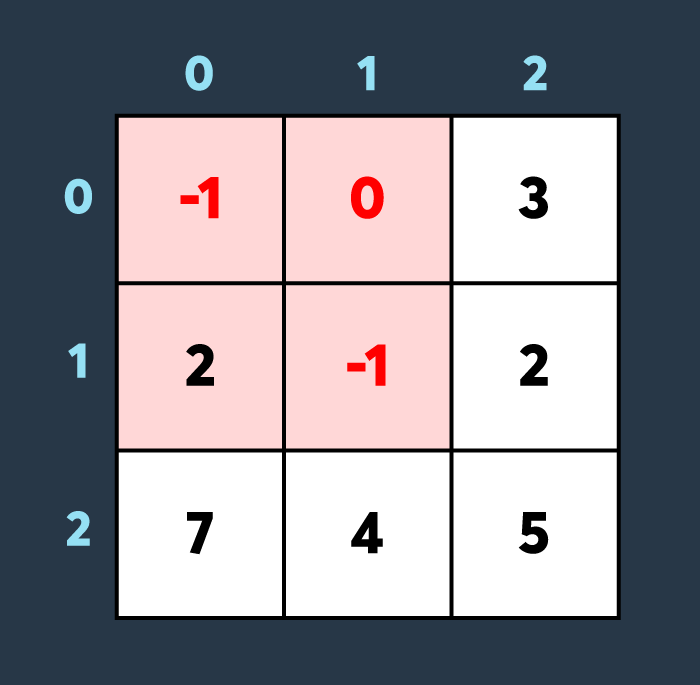
마지막으로 아군이 맵의 (2,0)부터 (2,0)까지 회복하여 100만큼 건물의 내구도를 높이면 아래와 같은 상황이 됩니다.

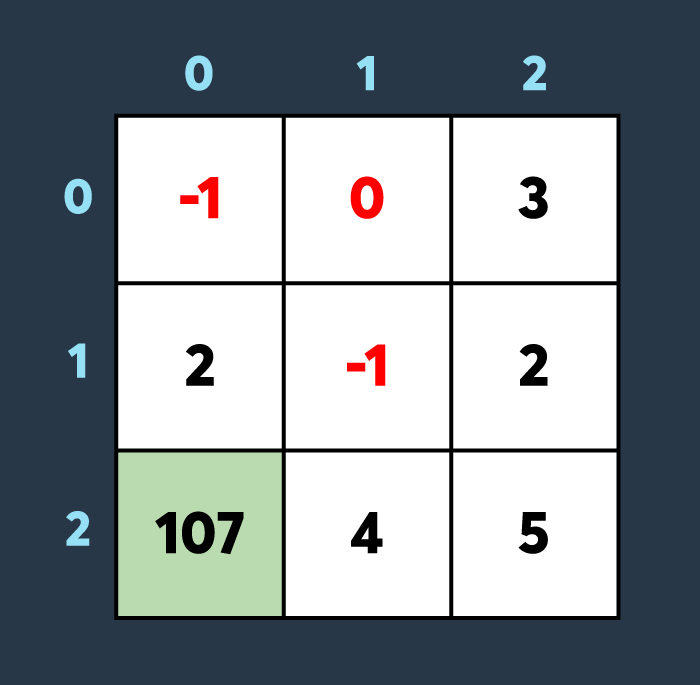
총, 6개의 건물이 파괴되지 않았습니다. 따라서 6을 return 해야 합니다.

---

나의 풀이

첫 번째 방법(이중 for문 순회)

package programmers;

public class IndestructibleBuilding {
	

	public static int solution(int[][] board, int[][] skill) {
       
        
        for(int[] nAttack : skill) {
        	int type = nAttack[0];
        	int degree = nAttack[5];
        	if(type == 1) {
        		for(int i = nAttack[1]; i <= nAttack[3]; i++) {
        			for(int j = nAttack[2]; j <= nAttack[4]; j++) {
        				board[i][j] -= degree;
        			}
        		}
        	}else {
        		for(int i = nAttack[1]; i <= nAttack[3]; i++) {
        			for(int j = nAttack[2]; j <= nAttack[4]; j++) {
        				board[i][j] += degree;
        			}
        		}
        		
        	}
        }
        
        int cnt = 0;
        for(int i = 0; i < board.length; i++) {
        	for(int j = 0; j < board[0].length; j++) {
        		if(board[i][j] > 0) {
        			cnt++;
        		}
        	}
        }
        
        
        return cnt;
    }
	
	public static void main(String[] args) {
		
		
		int[][] board = {{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5}};
		int[][] skill = {{1,0,0,3,4,4},{1,2,0,2,3,2},{2,1,0,3,1,2},{1,0,1,3,3,1}};
		solution(board, skill);
	}

}

누적합(Prefix Sum)

package programmers;

import java.util.Arrays;

public class IndestructibleBuilding {
	

	public static int solution(int[][] board, int[][] skill) {
       
        
        int N = board.length;
        int M = board[0].length;
        
        int[][] prefixSum = new int[N+1][M+1];
        
       
        for(int[] sk : skill) {
        	int type = sk[0];
        	int r1 = sk[1];
        	int c1 = sk[2];
        	int r2 = sk[3];
        	int c2 = sk[4];
        	int degree = (type == 1) ? -sk[5] : sk[5];
        	
        	prefixSum[r1][c1] += degree;
            prefixSum[r1][c2+1] -= degree;
            prefixSum[r2+1][c1] -= degree;
            prefixSum[r2+1][c2+1] += degree;
        }
        
        for (int i = 0; i <= N; i++) {
            for (int j = 1; j <= M; j++) {
                prefixSum[i][j] += prefixSum[i][j-1];
            }
        }

        
        for (int j = 0; j <= M; j++) {
            for (int i = 1; i <= N; i++) {
                prefixSum[i][j] += prefixSum[i-1][j];
            }
        }
		
        int count = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                board[i][j] += prefixSum[i][j];
                if (board[i][j] > 0) count++;
            }
        }
        
        return count;
    }
	
	public static void main(String[] args) {
		
		
		int[][] board = {{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5}};
		int[][] skill = {{1,0,0,3,4,4},{1,2,0,2,3,2},{2,1,0,3,1,2},{1,0,1,3,3,1}};
		solution(board, skill);
	}

}

---

나의 생각

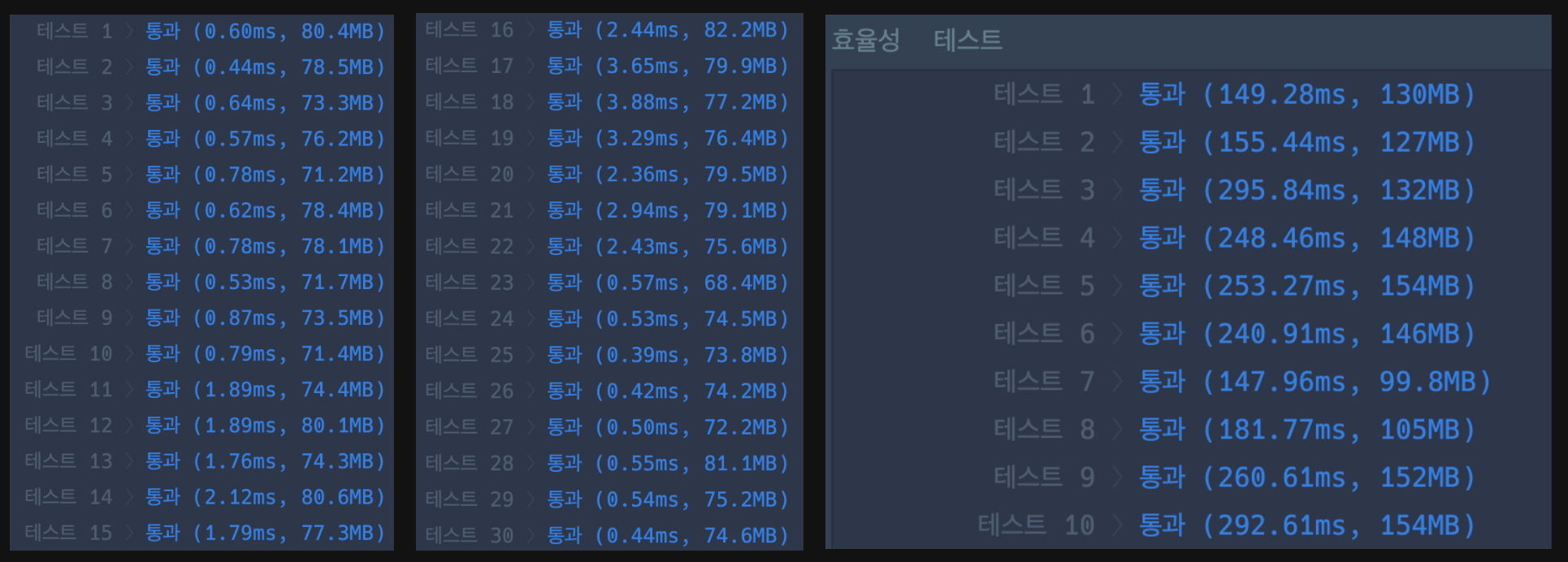
• 카카오 블라인드 코테 문제라기에 다소 어렵겠다라고 겁먹고 문제를 풀었다. 코테 문제들은 문제는 뭔가 내용이 엄청 많아 보이는데, 도출해야하는 결과값은 명확한거 같아 로직을 구현함에 있어 보다 자신있게 접근하였다. 문제를 보자마자 효율성 테스트 점수가 있는것을 보고 쌔한? 느낌을 먼저 받았지만 먼저 생각나는대로 문제를 풀었다. 처음 푼 방법은 단순 구현으로 문제를 풀었는데,
  type이 1인가? ,아닌가로 2차원 board 배열을 업데이트 하는 방식으로 문제를 풀었다.

아래의 결과를 보면 알 수 있듯이, 잘못된 풀이 방법은 아니나 효율성 테스트에서 시간초과로 실패했기때문에 더 빠른 방법으로 문제를 풀 수 있다는 의미로 해석된다. (엄밀히 따지고 보면 로직을 잘못 구성했기 때문에 실패한 로직)

💡 문제를 다시 생각해보면, 2차원 board 배열은 고정된 값을 가지고, 2차원 skill 배열의 값에 따라 board값이 변하는데, 한번의 반복으로 skill배열에 든 값을 계산, 저장하여 board에 결과를 추가하면 더 빠르게 문제를 풀 수 있겠다고 생각했다.

• 이때 사용 가능한 방법은 (누적합) prefixSum으로 누적합이란 2차원 배열에서 특정 범위에 대한 값을 빠르게 계산하기 위해 사용되며, 주어진 범위 내의 모든 값을 일일이 더하는 대신 배열의 특정 지점까지의 합을 미리 계산해두고 이를 이용하는 방식이다.

prefixSum 배열에서 하는 역할은 다음과 같다.

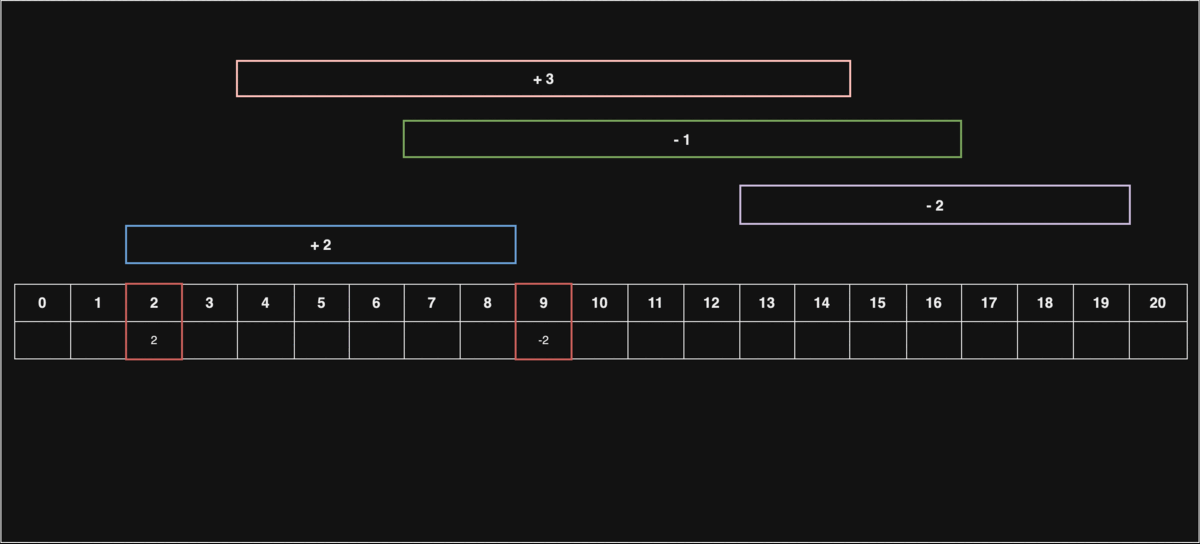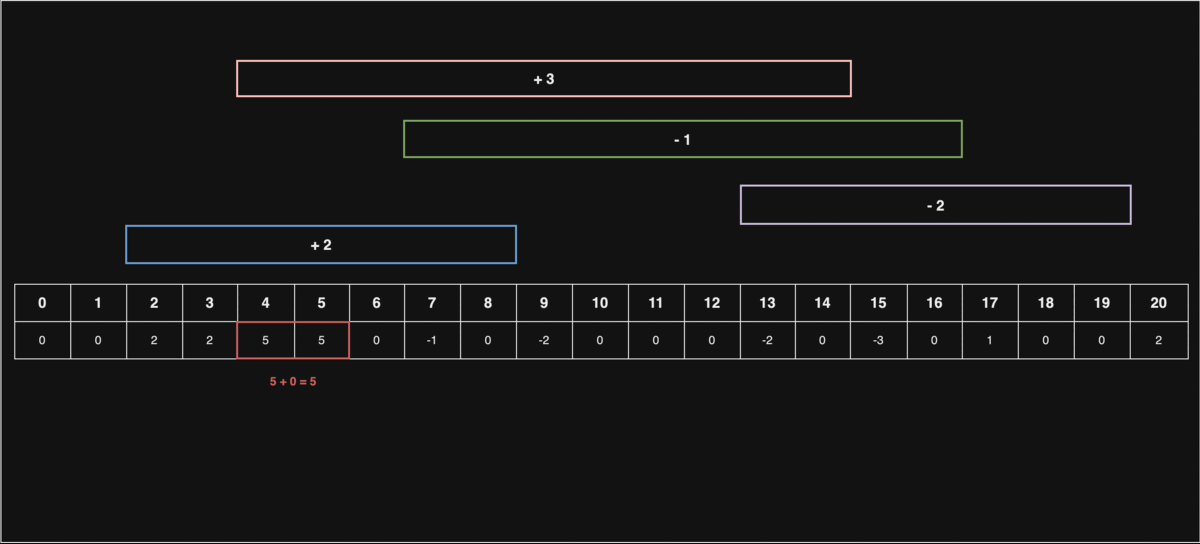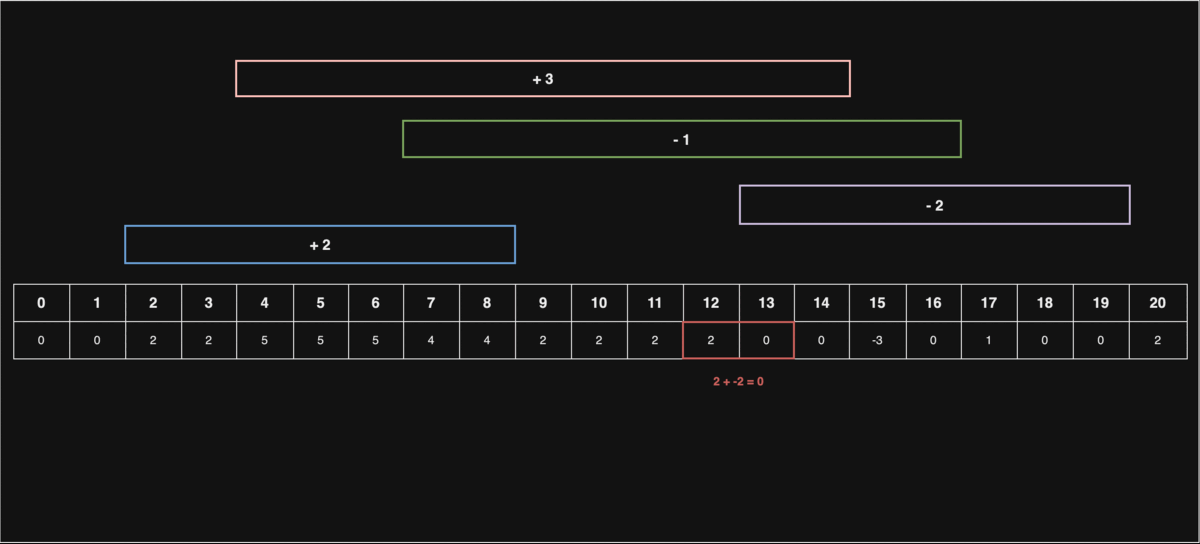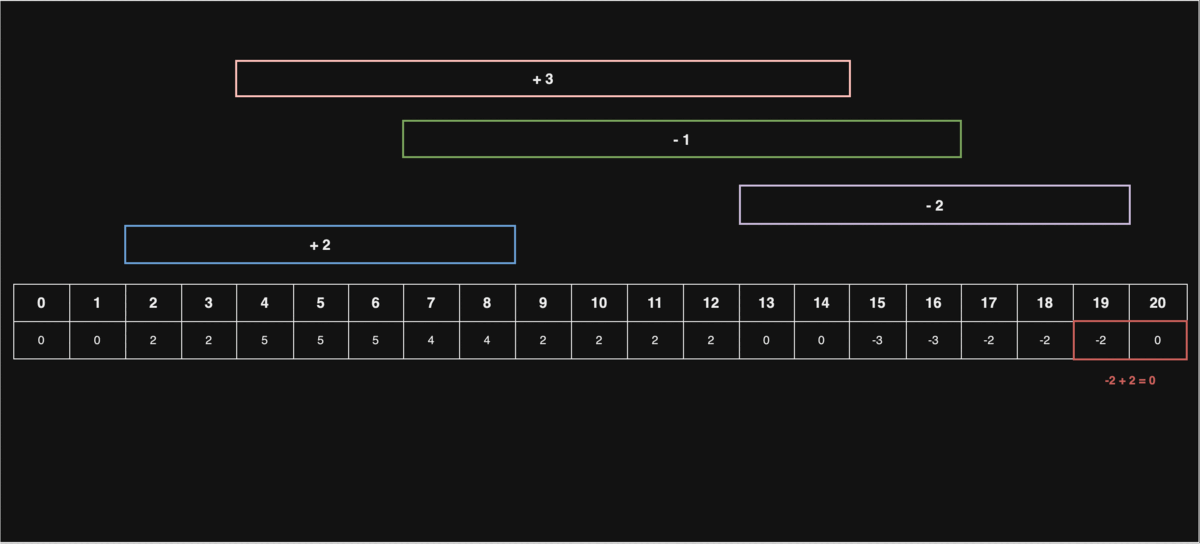
1. 범위 업데이트 : prefixSum 배열은 Skill의 각 조작을 반영하여,
   해당 조작이 적용되는 범위의 시작점과 끝점에 해당하는 누적합을 업데이트한다.
   이렇게 하면 나중에 한 번의 순회로 모든 업데이트를 반영할 수 있다.
2. 누적합 계산 : 범위 업데이트가 완료된 후, prefixSum 배열을 순회하며
   가로 방향과 세로 방향으로 누적합을 계산한다. 이 단계에서는 각 행의 시작부터
   현재 위치까지의 합과 각 열의 시작부터 현재 위치까지의 합을 계산하여
   배열의 각 위치에 대한 최종적인 누적합을 구한다.
3. 최종 값 적용 : 계산된 누적합을 원래의 board 배열에 적용

prefixSum(누적합)의 장점은 많은 수의 범위 업데이트와 쿼리가 있을 때, 각각을 개별적으로 처리하는 것보다 훨씬 더 빠르게 작동한다는 점이다. prefixSum은 각 범위 업데이트를 O(1) 시간에 처리할 수 있도록 하고 최종적인 배열의 값을 O(N * M) 시간에 계산할 수 있게 해준다.

prefixSum 배열 생성

경계값 적용

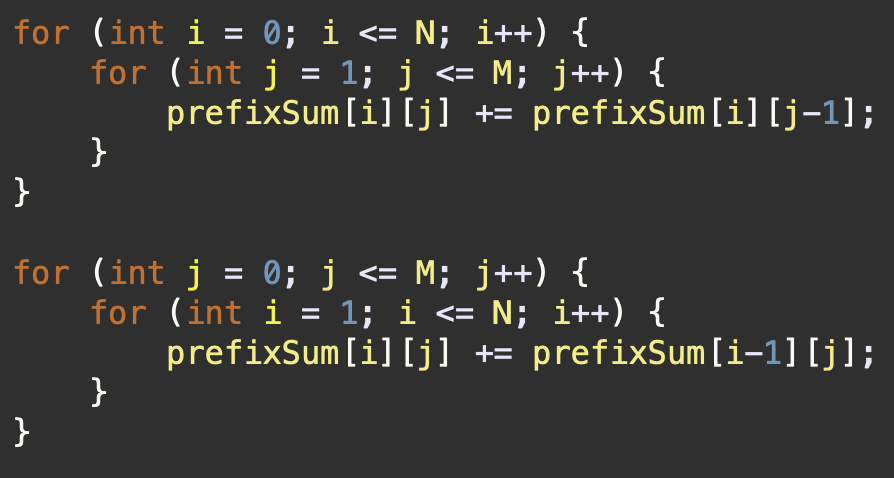
가로, 세로 방향 누적합(prefixSum)

2차원 board 배열에 누적합 업데이트

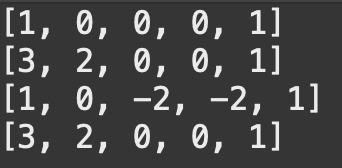
이중 for문 순회	누적합(Prefix Sum)

---

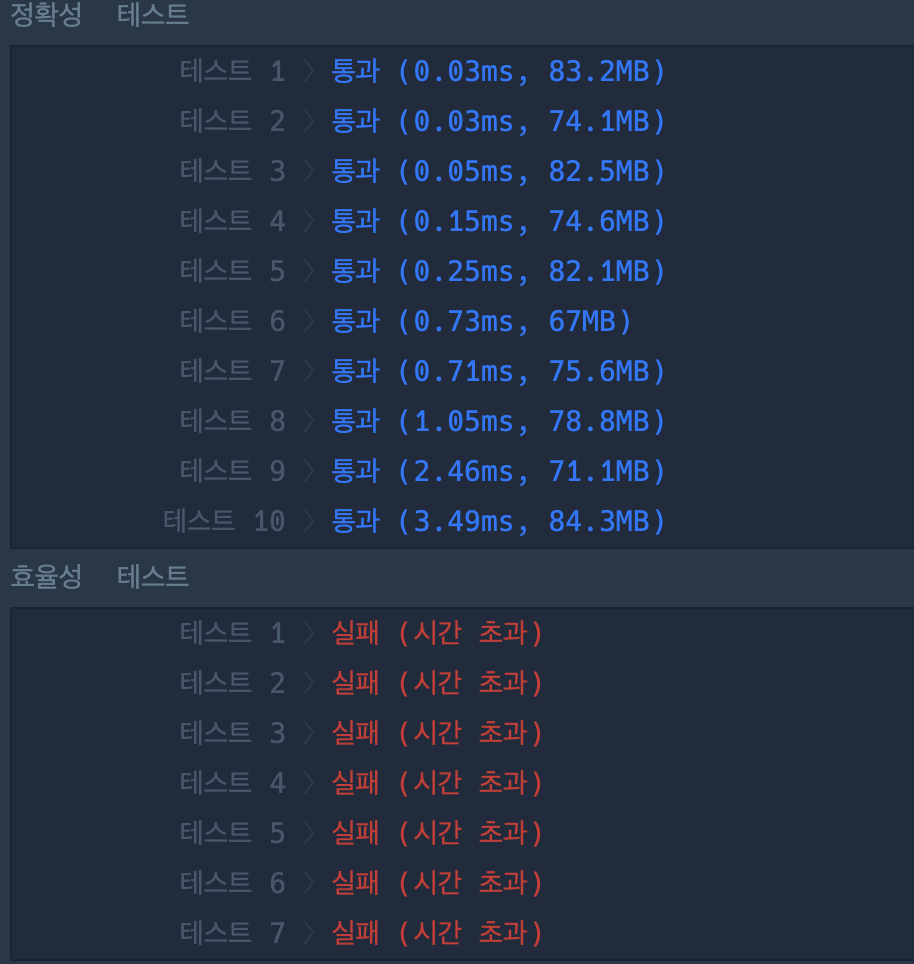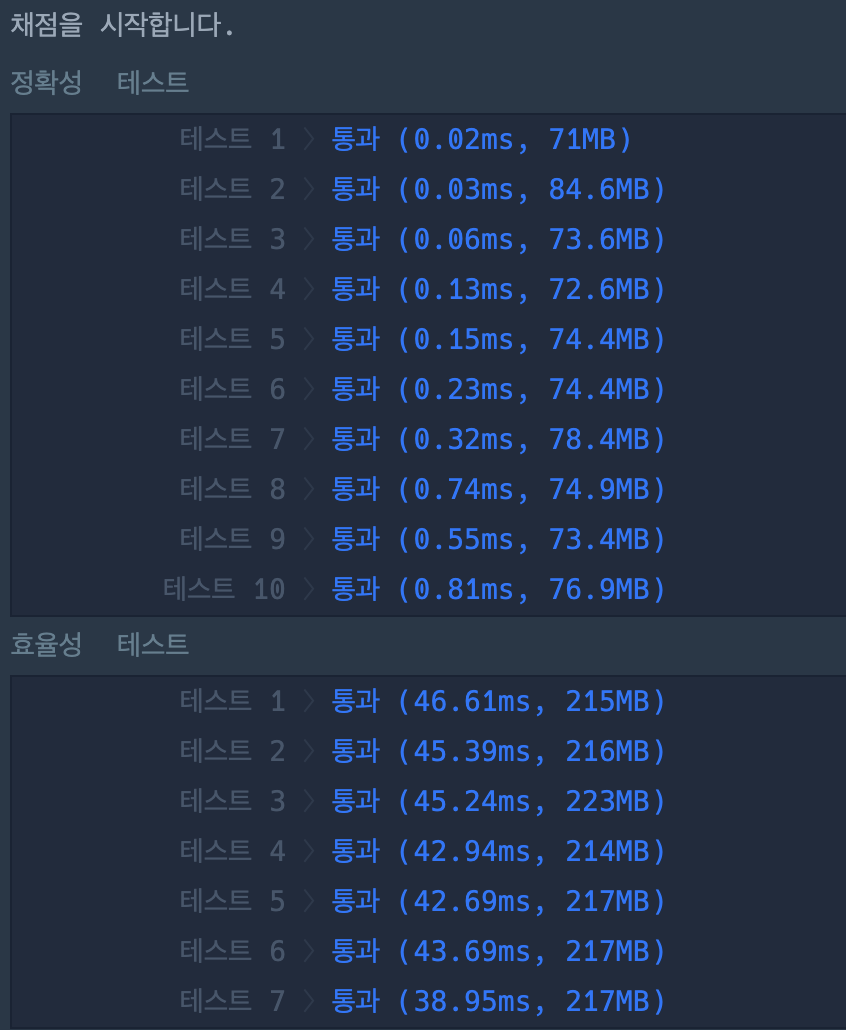표 편집

문4) 업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다

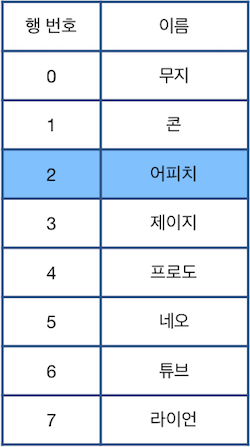
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.

• "U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
• "D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
• "C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
• "Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.

예를 들어 위 표에서 "D 2"를 수행할 경우 아래 그림의 왼쪽처럼 4행이 선택되며, "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "네오"가 적힌 행을 선택합니다(4행이 삭제되면서 아래 있던 행들이 하나씩 밀려 올라오고, 수정된 표에서 다시 4행을 선택하는 것과 동일합니다).

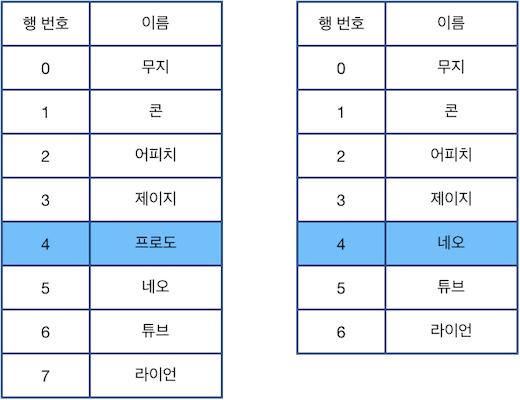
다음으로 "U 3"을 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다.

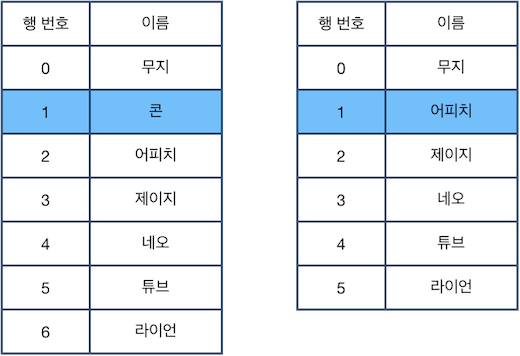
다음으로 "D 4"를 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다. 5행이 표의 마지막 행 이므로, 이 경우 바로 윗 행을 선택하는 점에 주의합니다.

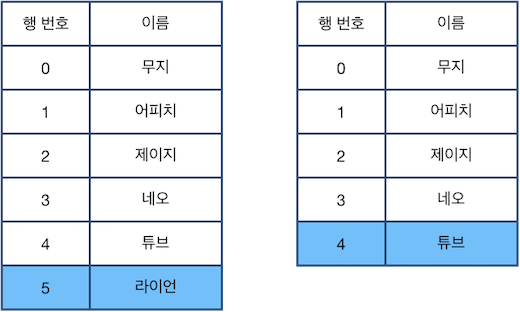
다음으로 "U 2"를 수행하면 현재 선택된 행은 2행이 됩니다.

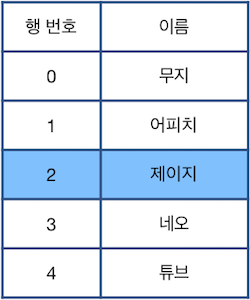
위 상태에서 "Z"를 수행할 경우 가장 최근에 제거된 "라이언"이 적힌 행이 원래대로 복구됩니다.

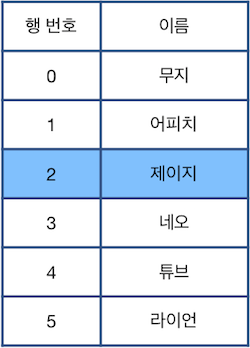
다시한번 "Z"를 수행하면 그 다음으로 최근에 제거된 "콘"이 적힌 행이 원래대로 복구됩니다. 이때, 현재 선택된 행은 바뀌지 않는 점에 주의하세요.

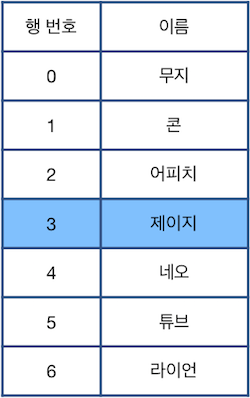
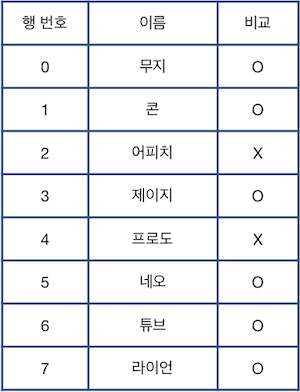
이때, 최종 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 "O", 삭제된 행은 "X"로 표시하면 다음과 같습니다.

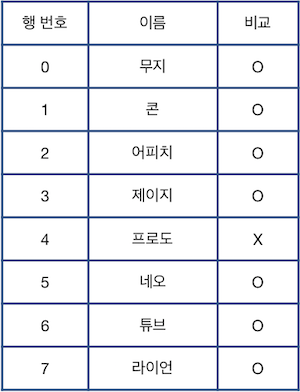
처음 표의 행 개수를 나타내는 정수 n, 처음에 선택된 행의 위치를 나타내는 정수 k, 수행한 명령어들이 담긴 문자열 배열 cmd가 매개변수로 주어질 때, 모든 명령어를 수행한 후 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 O, 삭제된 행은 X로 표시하여 문자열 형태로 return 하도록 solution 함수를 완성해주세요.

---

제한 사항

• 5 ≤ n ≤ 1,000,000
• 0 ≤ k < n
• 1 ≤ cmd의 원소 개수 ≤ 200,000
  • cmd의 각 원소는 "U X", "D X", "C", "Z" 중 하나입니다.
  • X는 1 이상 300,000 이하인 자연수이며 0으로 시작하지 않습니다.
  • X가 나타내는 자연수에 ',' 는 주어지지 않습니다. 예를 들어 123,456의 경우 123456으로 주어집니다.
  • cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.
  • 표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
  • 본문에서 각 행이 제거되고 복구되는 과정을 보다 자연스럽게 보이기 위해 "이름" 열을 사용하였으나, "이름"열의 내용이 실제 문제를 푸는 과정에 필요하지는 않습니다. "이름"열에는 서로 다른 이름들이 중복없이 채워져 있다고 가정하고 문제를 해결해 주세요.
• 표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
• 원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
• 정답은 표의 0행부터 n - 1행까지에 해당되는 O, X를 순서대로 이어붙인 문자열 형태로 return 해주세요.

정확성 테스트 케이스 제한 사항

• 5 ≤ n ≤ 1,000
• 1 ≤ cmd의 원소 개수 ≤ 1,000

효율성 테스트 케이스 제한 사항

• 주어진 조건 외 추가 제한사항 없습니다.

---

n	k	cmd	result
8	2	["D 2","C","U 3","C","D 4","C","U 2","Z","Z"]	"OOOOXOOO"
8	2	["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"]	"OOXOXOOO"

---

입출력 예 설명

입출력 예 #2

다음은 9번째 명령어까지 수행한 후의 표 상태이며, 이는 입출력 예 #1과 같습니다.

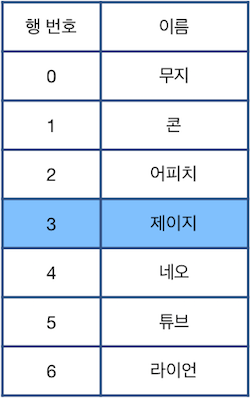
10번째 명령어 "U 1"을 수행하면 "어피치"가 적힌 2행이 선택되며, 마지막 명령어 "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "제이지"가 적힌 행을 선택합니다.

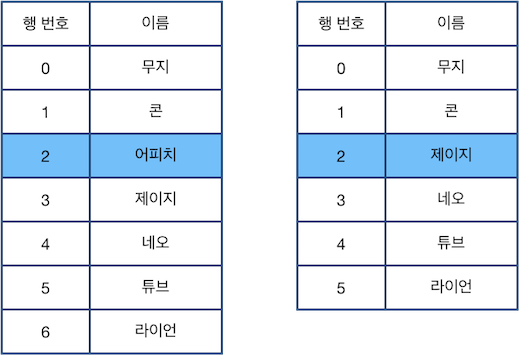
따라서 처음 주어진 표의 상태와 최종 표의 상태를 비교하면 다음과 같습니다.

---

나의 풀이

효율성 실패 로직

package programmers;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class EditTable {
	
	static class Remove{
		int index;
		char name;
		public Remove(int index, char name) {
			this.index = index;
			this.name = name;
		}
	}
	
	public static String solution(int n, int k, String[] cmd) {
    
        
        ArrayList<Character> originList = new ArrayList<>();
        Stack<Remove> removeIndexList = new Stack<>();
        
        for(char c = 'a'; c < 'a'+n; c++) {
        	originList.add(c);
        }
        
        ArrayList<Character> modifiedList = new ArrayList<>(originList);
        int currentIndex = k;
        
        for(int i = 0; i < cmd.length; i++) {
        	
        	char shortcutKey = cmd[i].charAt(0);
        	int move = 0;
        	if(cmd[i].length() > 1){
        		move = Integer.parseInt(cmd[i].split(" ")[1]);		
        	}
        	
        	if(shortcutKey == 'D' ) {
        		currentIndex += move;
    
        	}if(shortcutKey == 'U') {
        		currentIndex -= move;
        	}if(shortcutKey == 'C') {
        		char name = modifiedList.get(currentIndex);
        		removeIndexList.add(new Remove(currentIndex,name));
        		modifiedList.remove(currentIndex);
        		
        		if(currentIndex == modifiedList.size()) {
        			currentIndex--;
        		}
        		
        	}if(shortcutKey == 'Z') {
        		if(!removeIndexList.isEmpty()) {
        			Remove remove =	removeIndexList.pop();
        			int index = remove.index;
        			char name = remove.name;
        			modifiedList.add(index, name);
        			if(index <= currentIndex) {
        	            currentIndex++;
        	        }

        			
        		}
        	}
        }
        
        StringBuilder sb = new StringBuilder();
        
        for(char element : originList) {
        	if(modifiedList.contains(element)) {
        		sb.append("O");
            } else {
            	sb.append("X");
            }
        	
        }
        
        return sb.toString();
    }
	
	public static void main(String[] args) {
		String[] cmd = {"D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"};
		solution(8, 2, cmd);
	}

}

LinkedList를 사용한 효율성 실패 로직

package programmers;

import java.util.LinkedList;
import java.util.Stack;

public class EditTable {
	
	static class Node{
		int index;
		Node prev, next;
		
		public Node(int index) {
			this.index = index;
		}
	}
	
	public static String solution(int n, int k, String[] cmd) {
		
		LinkedList<Node> list = new LinkedList<>();
		
		for(int i = 0; i < n; i++) {
			list.add(new Node(i));
		}
		
		for (int i = 0; i < list.size(); i++) {
	        Node current = list.get(i);
	        if (i > 0) {
	            current.prev = list.get(i - 1); 
	        }
	        if (i < list.size() - 1) {
	            current.next = list.get(i + 1); 
	        }
	        
	    }
        
		

		
		Stack<Node> deletedNodes = new Stack<>();
		Node current = list.get(k);
		
		
		for(String command : cmd) {
			char shortcutKey = command.charAt(0);
			int move = 0;
			
			if(command.length() > 1) {
				move = Integer.parseInt(command.split(" ")[1]);
			}
			
			switch(shortcutKey) {
			case 'U' :
				for(int i = 0; i < move; i++) current = current.prev;
				break;
			
			case 'D' :
				for(int i = 0; i < move; i++) current = current.next;
				break;
			
			case 'C' :
				deletedNodes.push(current);
				if(current.next != null) current.next.prev = current.prev;
				if(current.prev != null) current.prev.next = current.next;
				
				if (current.next != null) {
                    current = current.next;
                } else {
                    current = current.prev;
                }
                break;
                
			case 'Z':
                Node node = deletedNodes.pop();
                if (node.prev != null) node.prev.next = node;
                if (node.next != null) node.next.prev = node;
                break;
			}
			
			Node temp = list.size() > 0 ? list.getFirst() : null;
		    while (temp != null) {
		        System.out.print(temp.index + " ");
		        temp = temp.next;
		    }
		    System.out.println();
		}
		
        StringBuilder sb = new StringBuilder("O".repeat(n));
        while (!deletedNodes.isEmpty()) {
            Node node = deletedNodes.pop();
            sb.setCharAt(node.index, 'X');
        }
        
        
        
        
        
        return sb.toString();
    }
	
	public static void main(String[] args) {
		String[] cmd = {"D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C","Z","Z"};
		solution(8, 2, cmd);
	}

}

Linked List를 직접 구현한 로직

package programmers;

import java.util.Stack;

public class EditTable {
	
	static class Node{
		int index;
		Node prev, next;
		boolean removed = false;
		
		public Node(int index) {
			this.index = index;
		}
		
		public Node delete() {
			this.removed = true;
			if(prev != null) prev.next = this.next;
			if(next != null) next.prev = this.prev;
			return next != null? next : prev;
		}
		
		public void restore() {
			this.removed = false;
			if(prev != null) prev.next = this;
			if(next != null) next.prev = this;
		}
	}
	
	public static String solution(int n, int k, String[] cmd) {
		
		Node[] nodes = new Node[n];
		Stack<Node> deletedNodes = new Stack<>();
		
		for(int i = 0; i < n; i++) {
			nodes[i] = new Node(i);
		}
		
		for(int i = 1; i < n; i++) {
			nodes[i - 1].next = nodes[i];
			nodes[i].prev = nodes[i - 1];
		}
		
		Node currnetIndex = nodes[k];
		
		for(String command : cmd) {
			char shortcutKey = command.charAt(0);
			int move = 0;
			
			if(command.length() > 1) {
				move = Integer.parseInt(command.split(" ")[1]);
			}
			
			switch(shortcutKey) {
			case 'U' :
				while(move-- > 0) currnetIndex = currnetIndex.prev;
				break;
			case 'D':
				while(move-- > 0)currnetIndex = currnetIndex.next;
				break;
			case 'C':
				deletedNodes.push(currnetIndex);
				currnetIndex = currnetIndex.delete();
				break;
			case 'Z':
				deletedNodes.pop().restore();
				break;
			}
		}
		StringBuilder sb = new StringBuilder("O".repeat(n));
		while(!deletedNodes.isEmpty()) {
			Node node = deletedNodes.pop();
			if(node.removed) {
				sb.setCharAt(node.index, 'X');
			}
		}
        
        return sb.toString();
    }
	
	public static void main(String[] args) {
		String[] cmd = {"D 2","C","U 3","C","D 4","C","U 2","Z","Z"};
		solution(8, 2, cmd);
	}

}

---

나의 생각

정답 로직

처음 내가 생각한 아이디어는 다음과 같다.

1. 리스트를 하나 선언하고, n개에 해당하는 값을 리스트에 할당한다.
   👉🏻 n = 8이라면, 리스트에는 {a,b,c,d,e,f,g,h}를 할당
2. 제거되는 리스트는 Stack(LIFO) 자료구조를 사용하여, 제거된 항목 중, 가장 마지막 제거 항목부터 다시 불러올 수 있도록 한다. 단, Stack의 파라미터 타입은 index와 name 형태로 구성되어있다.
   👉🏻 Stack에 {0,a},{1,b},{2,c}가 차례로 push된다면, {2,c},{1,b},{0,a} 순서로 pop된다.
3. 매개 변수로 주어지는 명령어 U(Up), D(Down), C(Remove), Z(Restore) 의 기능을 가지고 있기때문에 if문이나, switch문으로 이 명령어를 먼저 선별할 것.
   👉🏻 U, D는 뒤에 몇 칸 이동 할 지 숫자가 따라 오기때문에, 이 숫자도 따로 선별할 것
4. 최종적으로 원본 리스트와, 원본을 복사한 modify한 리스트와 비교

위 아이디어를 바탕으로 로직을 구현하고, 테스트 했을때는 모든 테스트 조건이 통과하여 제출을 하였지만 보기좋게 실패...

실패 로직

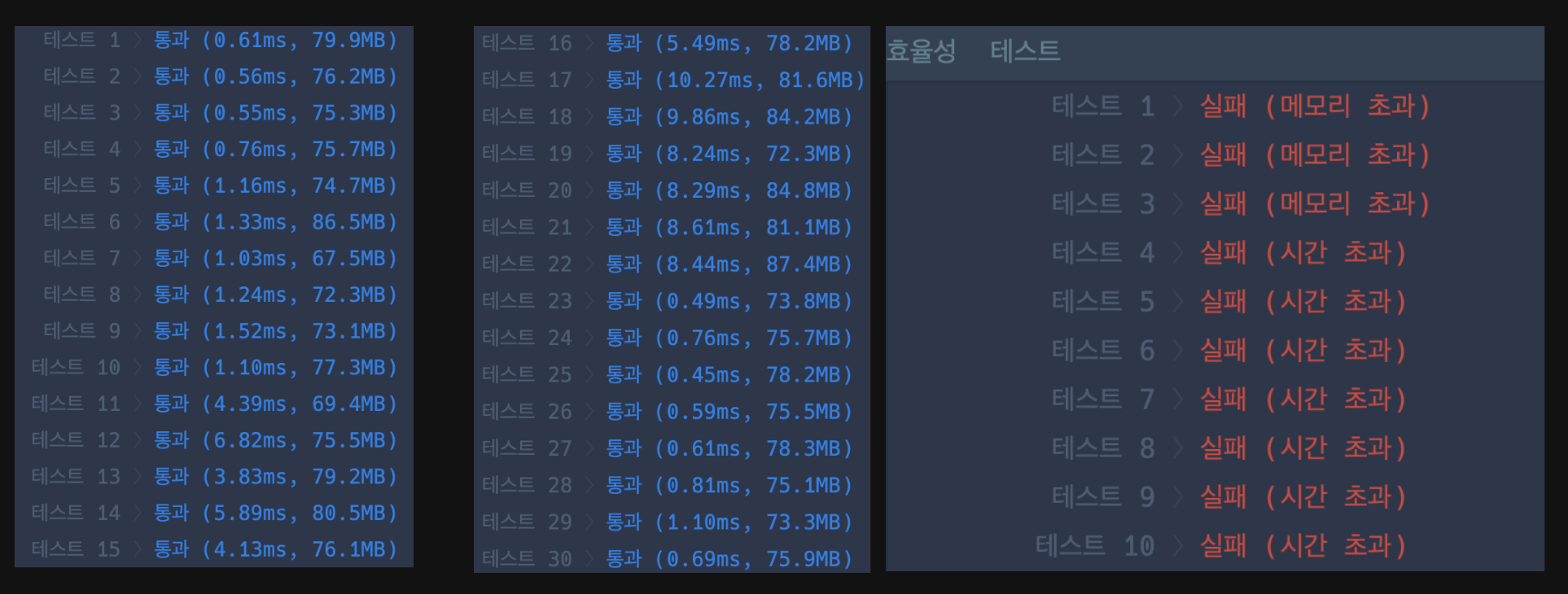
실패 로직을 보고 떠올랐던 생각은 카카오에서 이 문제로 채용을 진행한다면, 문제에 그 의도가 있지 않을까? 라는 생각을 먼저하게 되었다.
만약, DB에서 3천만개에 해당하는 테이블이 있다면, 내가 원하는 자료에 어떻게 쉽고 빠르게 접근할 수 있을까?
💡 즉, 단순 구현이 목적이 아니라, 제한된 상황에서 보다 쉽고 빠르게 원하는 데이터를 얻을 수 있는가를 중점으로 다시 생각을 해보았다.

그렇다면 나의 로직의 문제는 무엇일까?

1. 효율성 문제

• ArrayList의 remove와 add 연산 : 이러한 연산들은 ArrayList에서 비효율적일 수 있다. 특히, 중간에 있는 요소를 삭제하거나 추가할 때, 삭제된 요소 이후의 모든 요소를 한 칸씩 이동해야 하므로, 이러한 연산의 시간 복잡도는 O(n)이다. 대용량 데이터 처리 시, 이는 상당한 성능 저하를 야기할 수 있다.
• contains 메서드 사용 : contains 메서드 또한 내부적으로는 리스트를 순회하여 요소를 찾기 때문에 시간 복잡도가 O(n)이다. 최종적으로 상태 문자열을 생성할 때 모든 요소에 대해 contains를 호출하므로, 이 과정 또한 매우 비효율적이다.

2. 대용량 트래픽 및 빠른 응답 필요성 문제

• 대용량 처리 능력 부족 : 대용량 데이터에 대한 처리가 요구될 때, ArrayList의 remove와 add 연산의 비효율성은 처리 시간을 크게 증가시킬 수 있다. 때문에 이는 사용자에게 느린 응답 시간으로 이어질 수 있다.
• 삭제된 요소 복구 로직 : 삭제된 요소를 복구할 때, 해당 요소를 원래 위치에 정확히 삽입하는 처리가 필요하다. 이 과정에서 add 메서드를 사용하면 리스트의 나머지 부분을 조정해야 하므로, 대용량 데이터 처리 시 성능 저하의 원인이 된다.
• 응답 시간 증가 : 삭제나 복구, 현재 상태 확인 등의 연산이 빈번하게 발생하는 환경에서는, 각 연산의 처리 시간이 중요하다. 특히, DB에 대한 빠른 접근이 필요한 상황에서는, 위 로직의 비효율성이 심각한 지연을 초래할 수 있다.

개선 방안은?

연결 리스트 사용 : 삭제와 삽입이 빈번하게 발생하는 경우, 연결 리스트를 사용하면 각 연산을 O(1) 시간에 처리할 수 있다.
인덱스 관리 최적화 : 삭제된 요소의 인덱스를 관리하는 방식을 최적화하여, 복구 시 계산이 필요한 인덱스 조정을 최소화한다. 삭제된 요소를 스택에 저장할 때, 실제 삭제된 위치 정보를 함께 관리함으로써 복구 과정의 효율성을 높일 수 있다.
상태 확인 최적화 : 최종 상태를 확인할 때 contains 대신 더 효율적인 방법을 사용할 수 있다. 예를 들어, 삭제 여부를 나타내는 별도의 배열을 관리하여, 각 행의 상태를 O(1) 시간에 접근할 수 있도록 할 수 있다.

ArrayList와 LinkedList의 특징 및 장・단점

자료구조	주요 특징	장점	단점
ArrayList	- 인덱스 기반 데이터 접근 - 크기가 가변적으로 변함 - 연속된 메모리 위치 사용	- 데이터의 인덱스를 통한 빠른 접근 가능 - 데이터 추가 및 삭제 시 자동으로 크기 조정	- 데이터 추가 및 삭제 시 시간 복잡도가 O(n) - 크기 변경 시 메모리 재할당과 데이터 복사가 발생
LinkedList	- 데이터가 노드의 형태로 저장됨 - 각 노드는 다음 노드를 참조 - 추가적인 메모리 공간 사용	- 데이터 추가 및 삭제 시 빠른 처리 가능 - 크기 변경이 유연함	- 인덱스를 통한 데이터 접근 시 시간 복잡도가 O(n) - 추가적인 메모리 공간(노드의 참조) 필요

❗️ LinkedList로 구현 후 효율성 테스트 실패가 되었기 때문에, LinkedList를 직접 구현해보기로 함

Node 객체 배열을 크기 n으로 선언하고, 반복문을 사용하여 각 인덱스에 Node 객체를 생성하여 할당함

위 로직을 예로보면 i = 1일때

• nodes[0].next = nodes[1];
• nodes[1].prev = nodes[0];

각 노드들이 다음과 같이 연결됨을 알 수 있다.

다음으로 Node currentIndex = nodes[k] 인데, 이는 2번 노드부터 시작함을 알 수 있다.

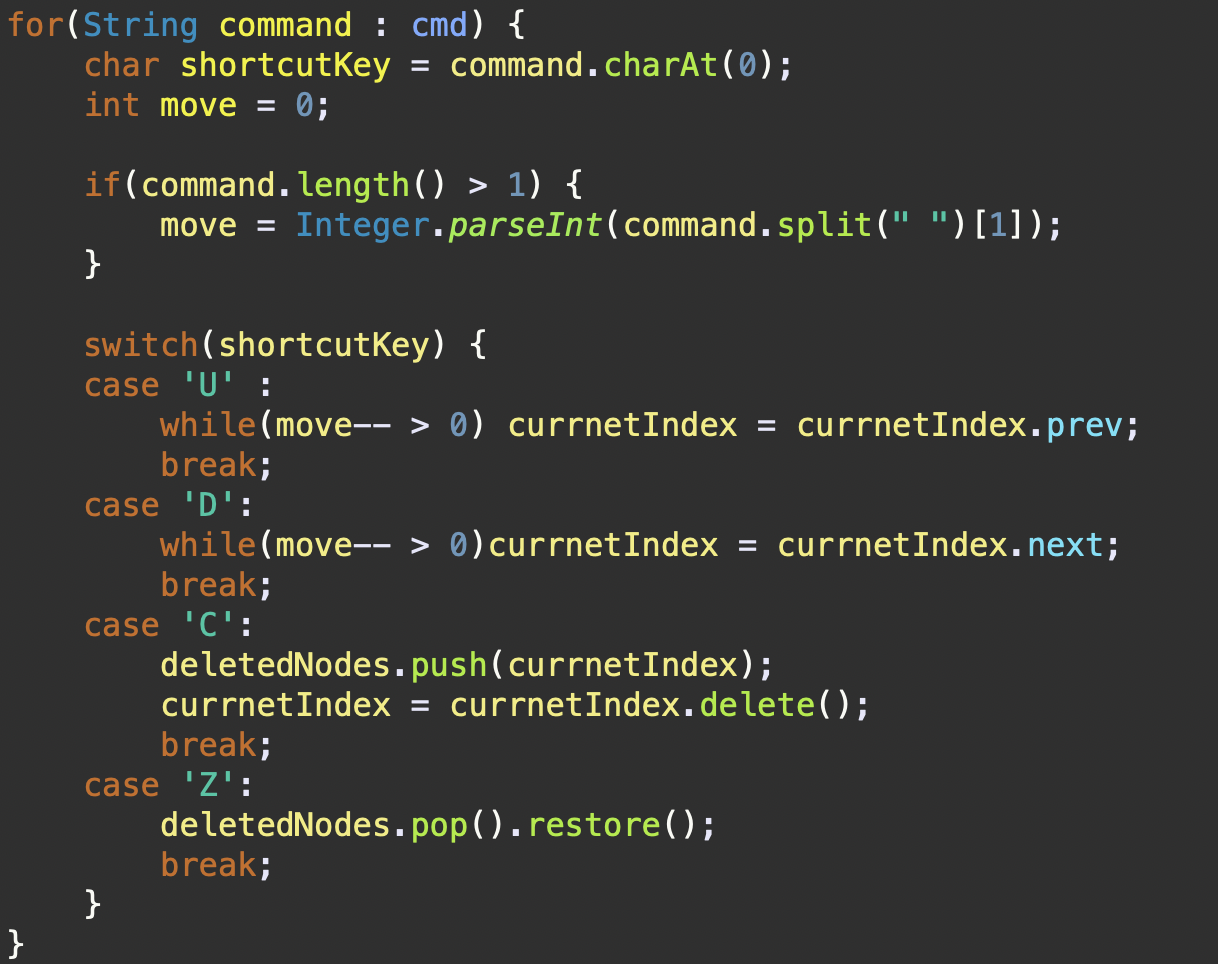
String[] cmd = {"D 2","C","U 3","C","D 4","C","U 2","Z","Z"}에 대해 각 단계에서 currentIndex의 변화를 설명하겠다.

초기 상태

1. D 2 명령어(2칸 아래로 이동)

• currentIndex는 처음 노드 2를 가리킨다.
• 첫 번째 반복 : move가 1 감소하여 1이된다. currentIndex는,current.next. 즉, 노드 3을 가리키게 된다.
• 두 번째 반복 : move가 다시 1 감소하여 0이 된다. currentIndex는,current.next. 즉, 노드 4를 가리키게 된다.
  

2. C 명령어(현재 선택된 노드 삭제)

• shortcutKey = 'C'
• deletedNodes 스택에 현재 currentIndex(nodes[4])를 푸시
• currentIndex를 nodes[4].delete()로 업데이트한다.
  만약 nodes[4]가 마지막 노드였다면 prev를, 그렇지 않다면 next를 가리키게 된다. 이 경우 nodes[5]를 가리키게 된다.
  

3. U 3 명령어(3칸 위로 이동)

• shortcutKey = 'U',move = 3
• currentIndex가 현재 nodes[5]를 가리키고 있다.
• while 루프를 세 번 실행한다
  • 첫 번째 반복 : currentIndex를 nodes[5].prev. 즉, nodes[3]로 업데이트
  • 두 번째 반복 : currentIndex를 node[3].prev. 즉, nodes[2]로 업데이트
  • 세 번쨰 반복 : currentIndex를 nodes[2].prev. 즉, nodes[1]로 업데이트
• currentIndex는 이제 nodes[2]를 가리킨다.
  

4. C 명령어(현재 선택된 노드 삭제)

• shortcutKey = 'C'
• deletedNodes 스택에 현재 currentIndex(nodes[1])를 푸시
• currentIndex를 node[1].delete()로 업데이트 한다.
  이 경우 nodes[2]를 가리키게 된다.
  

5. D 4 명령어(4칸 아래로 이동)

• shortcutKey = 'D',move = 4
• currentIndex가 현재 nodes[2]를 가리키고 있다.
• while 루프를 네 번 실행한다. 이동 중 삭제된 노드는 건너뛰고, 실제 존재하는 노드로 이동한다.
• currentIndex는 이제 마지막 노드를 가리킨다.
  

6. C 명령어(현재 선택된 노드 삭제)

• shortcutKey = 'C'
• deletedNodes 스택에 현재 currentIndex(nodes[7])를 푸시
• currentIndex를 node[7].delete()를 실행하여 삭제되고, 삭제된 노드가 리스트의 마지막 노드였기 때문에, prev 노드인 nodes[6]을 가리키게 된다.
  

7. U 2 명령어(2칸 위로 이동)

• shortcutKey = 'U', move = 2
• currentIndex는 현재 nodes[6]를 가리키고 있습니다.
  • 첫 번째 반복: currentIndex는 nodes[6].prev, 즉 nodes[5]를 가리키게 된다.
  • 두 번째 반복: currentIndex는 nodes[5].prev, 즉 nodes[3]를 가리키게 된다.
• currentIndex는 이제 nodes[3]을 가리킨다.
  

8. Z 명령어(삭제된 마지막 행 복구)

• shortcutKey = 'Z'
• 삭제된 마지막 노드 [7]을 복구하며, 이때 restore() 메서드가 호출되어, 노드 [7]의 removed플래그가 false로 설정되고 이전 노드 [6]의 next 포인트가 노드 [7]을 가리키도록 설정된다. 동시에 노드 [7]의 prev 포인트는 노드 [6]을 가리키게 된다.
• 이 과정에서 중요한 점은 노드 [7]에 들어 있는 prev,next값이 삭제 시점에 메모리에서 유지된다는 것이다. 즉, 노드 [7]이 삭제되었다가 복구될 때, 이 노드는 여전히 원래의 prev(노드[6]),next(null) 연결 정보를 가지고 있어서, 연결 리스트 내에서 정확한 위치로 복구될 수 있다.
  💡 즉, 삭제된 노드의 prev 및 next 정보는 해당 노드 객체 내에 계속해서 유지되므로, 삭제 이후에도 이 정보를 기반으로 리스트에 다시 삽입될 수 있다.
  
  삭제된 노드 [7]이 복구되어도 여전히 currentIndex는 node[3]을 가리킨다.

9. Z 명령어(삭제된 마지막 행 복구)

• shortcutKey = 'Z'
• deletedNodes 스택에서 또 다른 노드를 pop하여 복구한다. 이번에 복구되는 노드는 노드[1]이다.
• resotre() 메서드를 호출하여 노드 [1]을 복구한다. 이 과정에서 노드 [1]의 removed 플래그가 false로 설정되고, 이전 노드의 next포인터와 다음 노드의 prev 포인터가 각각 노드 [1]을 가리키도록 재설정된다.
  • 마찬가지로, 삭제 시 노드 [1]의 prev와next 정보는 메모리에 남아 있어 복구 과정에서 사용된다.
    

삭제된 행 상태를 문자열로 변환하기

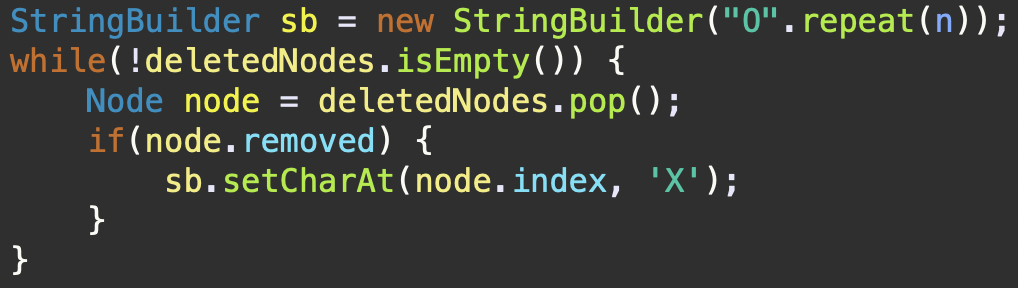
1. StringBuilder객체 sb를 생성하고, n의 길이만큼 O 문자로 초기화한다. 이는 모든 행이 처음에는 삭제되지 않았음을 의미한다.
2. deletedNodes 스택이 비어있지 않는 동안, 즉 삭제된 노드가 있다면, 다음 단계를 반복한다.
   • deletedNodes 스택에서 하나의 노드를 팝(pop)하여 Node node 변수에 할당한다. 여기서 pop() 메서드는 스택의 최상위에 있는 노드를 반환하고 스택에서 해당 노드를 제거한다.
3. if(node.removed) 조건문을 사용하여 팝된 노드가 삭제된 노드인지 확인한다. 삭제된 노드는 removed 속성이 true로 설정되어 있다.
4. 조건문이 true일 경우(노드가 삭제되었을 경우), sb의 setCharAt메서드를 사용하여 해당 노드 인덱스에 해당하는 위치의 문자를 X로 변경한다.
5. 이 과정이 모든 삭제된 노드에 대해 반복되고, 최종적으로 sb는 삭제되지 않은 행은 O, 삭제된 행은 X로 표시된 문자열을 가지게 된다.

---

길 찾기 게임

문5) 전무로 승진한 라이언은 기분이 너무 좋아 프렌즈를 이끌고 특별 휴가를 가기로 했다.
내친김에 여행 계획까지 구상하던 라이언은 재미있는 게임을 생각해냈고 역시 전무로 승진할만한 인재라고 스스로에게 감탄했다.

라이언이 구상한(그리고 아마도 라이언만 즐거울만한) 게임은, 카카오 프렌즈를 두 팀으로 나누고, 각 팀이 같은 곳을 다른 순서로 방문하도록 해서 먼저 순회를 마친 팀이 승리하는 것이다.

그냥 지도를 주고 게임을 시작하면 재미가 덜해지므로, 라이언은 방문할 곳의 2차원 좌표 값을 구하고 각 장소를 이진트리의 노드가 되도록 구성한 후, 순회 방법을 힌트로 주어 각 팀이 스스로 경로를 찾도록 할 계획이다.

라이언은 아래와 같은 특별한 규칙으로 트리 노드들을 구성한다.

• 트리를 구성하는 모든 노드의 x, y 좌표 값은 정수이다.
• 모든 노드는 서로 다른 x값을 가진다.
• 같은 레벨(level)에 있는 노드는 같은 y 좌표를 가진다.
• 자식 노드의 y 값은 항상 부모 노드보다 작다.
• 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
• 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.

아래 예시를 확인해보자.

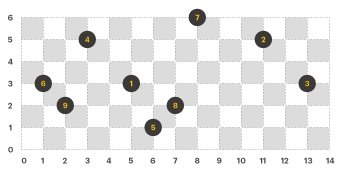
라이언의 규칙에 맞게 이진트리의 노드만 좌표 평면에 그리면 다음과 같다. (이진트리의 각 노드에는 1부터 N까지 순서대로 번호가 붙어있다.)

이제, 노드를 잇는 간선(edge)을 모두 그리면 아래와 같은 모양이 된다.

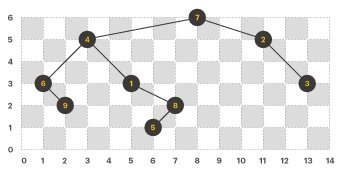
위 이진트리에서 전위 순회(preorder), 후위 순회(postorder)를 한 결과는 다음과 같고, 이것은 각 팀이 방문해야 할 순서를 의미한다.

• 전위 순회 : 7, 4, 6, 9, 1, 8, 5, 2, 3
• 후위 순회 : 9, 6, 5, 8, 1, 4, 3, 2, 7

다행히 두 팀 모두 머리를 모아 분석한 끝에 라이언의 의도를 간신히 알아차렸다.

그러나 여전히 문제는 남아있다. 노드의 수가 예시처럼 적다면 쉽게 해결할 수 있겠지만, 예상대로 라이언은 그렇게 할 생각이 전혀 없었다.

이제 당신이 나설 때가 되었다.

곤경에 빠진 카카오 프렌즈를 위해 이진트리를 구성하는 노드들의 좌표가 담긴 배열 nodeinfo가 매개변수로 주어질 때,
노드들로 구성된 이진트리를 전위 순회, 후위 순회한 결과를 2차원 배열에 순서대로 담아 return 하도록 solution 함수를 완성하자.

---

제한 사항

• nodeinfo는 이진트리를 구성하는 각 노드의 좌표가 1번 노드부터 순서대로 들어있는 2차원 배열이다.
  • nodeinfo의 길이는 1 이상 10,000 이하이다.
  • nodeinfo[i] 는 i + 1번 노드의 좌표이며, [x축 좌표, y축 좌표] 순으로 들어있다.
  • 모든 노드의 좌표 값은 0 이상 100,000 이하인 정수이다.
  • 트리의 깊이가 1,000 이하인 경우만 입력으로 주어진다.
  • 모든 노드의 좌표는 문제에 주어진 규칙을 따르며, 잘못된 노드 위치가 주어지는 경우는 없다.

---

입출력 예

nodeinfo	result
[[5,3],[11,5],[13,3],[3,5],[6,1],[1,3],[8,6],[7,2],[2,2]]	[[7,4,6,9,1,8,5,2,3],[9,6,5,8,1,4,3,2,7]]

---

나의 풀이

package programmers;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;



class Node implements Comparable<Node>{
	
	int x, y, id; // 노드의 x, y 좌표와 고유 식별자
    Node left, right; // 왼쪽 및 오른쪽자식 노드에 대한 참조
    
    // 노드 생성자
    Node(int x, int y, int id) {
        this.x = x;
        this.y = y;
        this.id = id;
    }
    
    // Comparable 인터페이스 구현 - 노드를 y 좌표에 따라 정렬, y가 같으면 x에 따라 정렬
	@Override
	public int compareTo(Node other) {
		if(this.y == other.y) return this.x - other.x;
		return other.y - this.y;
	}
	
}

public class PathFindingGame {
	
	static Node root; // 이진 트리의 루트 노드
	static List<Integer> preOrderList = new ArrayList<>(); // 전휘 순회
	static List<Integer> postOrderList = new ArrayList<>(); // 후휘 순회
	
	public static void insert(Node parent, Node child) {
		// 삽입할 노드의 x 좌표가 부모 노드보다 작으면 왼쪽 자식으로 삽입
		if(child.x < parent.x) {
			if(parent.left == null) {
				parent.left = child;
			}else {
				insert(parent.left, child); // 재귀적으로 왼쪽 서브트리 탐색
			}
		}else { // 삽입할 노드의 x 좌표가 부모 노드보다 크거나 같으면 오른쪽 자식으로 삽입
			if(parent.right == null) {
				parent.right = child;
			}else {
				insert(parent.right, child); // 재귀적으로 오른쪽 서브트리 탐색
			}
		}
	}
	// 전위 순회 메서드
	public static void preOrder(Node node) {
		if(node == null) return; // 기저조건 : 노드가 null이면 반환
		preOrderList.add(node.id); // 현재 노드 처리 (노드의 id 저장)
		preOrder(node.left); // 왼쪽 서브트리 순회
		preOrder(node.right); // 오른쪽 서브트리 순회
	}
	// 후위 순회 메서드
	public static void postOrder(Node node) {
        if (node == null) return; // 기저조건 : 노드가 null이면 반환
        postOrder(node.left); // 왼쪽 서브트리 순회
        postOrder(node.right); // 오른쪽 서브트리 순회
        postOrderList.add(node.id); // 현재 노드 처리 (노드의 id 저장)
    }
	
	public static int[][] solution(int[][] nodeinfo) {
        // 노드 객체를 저장할 리스트
		List<Node> nodes = new ArrayList<>();
		// 노드 정보를 바탕으로 Node 객체 생성 및 리스트에 추가
		for(int i= 0 ; i < nodeinfo.length; i++) {
			nodes.add(new Node(nodeinfo[i][0], nodeinfo[i][1], i+1));
		}
		
		// // 노드를 y 좌표에 따라 정렬 (내림차순), y가 같으면 x에 따라 정렬
		Collections.sort(nodes);
		
		root = nodes.get(0); // 정렬된 리스트의 첫 번째 노드를 루트로 설정
		// 나머지 노드들을 트리에 삽입
		for(int i = 1; i < nodes.size(); i++) {
			insert(root, nodes.get(i));
		}
		
		preOrder(root); // 전위 순회
        postOrder(root); // 후위 순회

        int[][] answer = new int[2][nodeinfo.length];
        for (int i = 0; i < nodeinfo.length; i++) {
            answer[0][i] = preOrderList.get(i);
            answer[1][i] = postOrderList.get(i);
        }
        
        
        for(int[] a : answer) {
        	System.out.println(Arrays.toString(a));
        }
        
        
        return answer;
	
    }
	
	public static void main(String[] args) {
		int[][] nodeinfo = {{5,3},{11,5},{13,3},{3,5},{6,1},
				{1,3},{8,6},{7,2},{2,2}};
		solution(nodeinfo);
	}

}

---

나의 생각

매개변수 nodeInfo

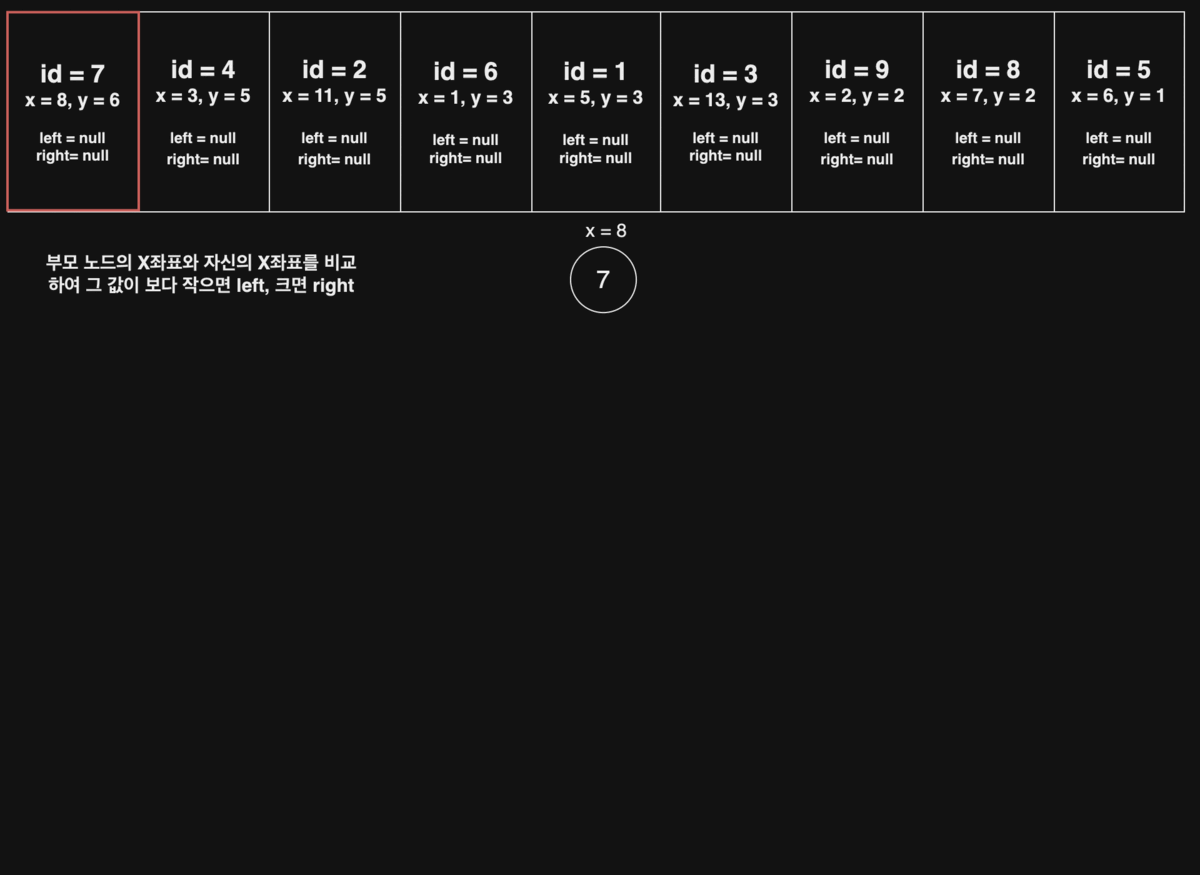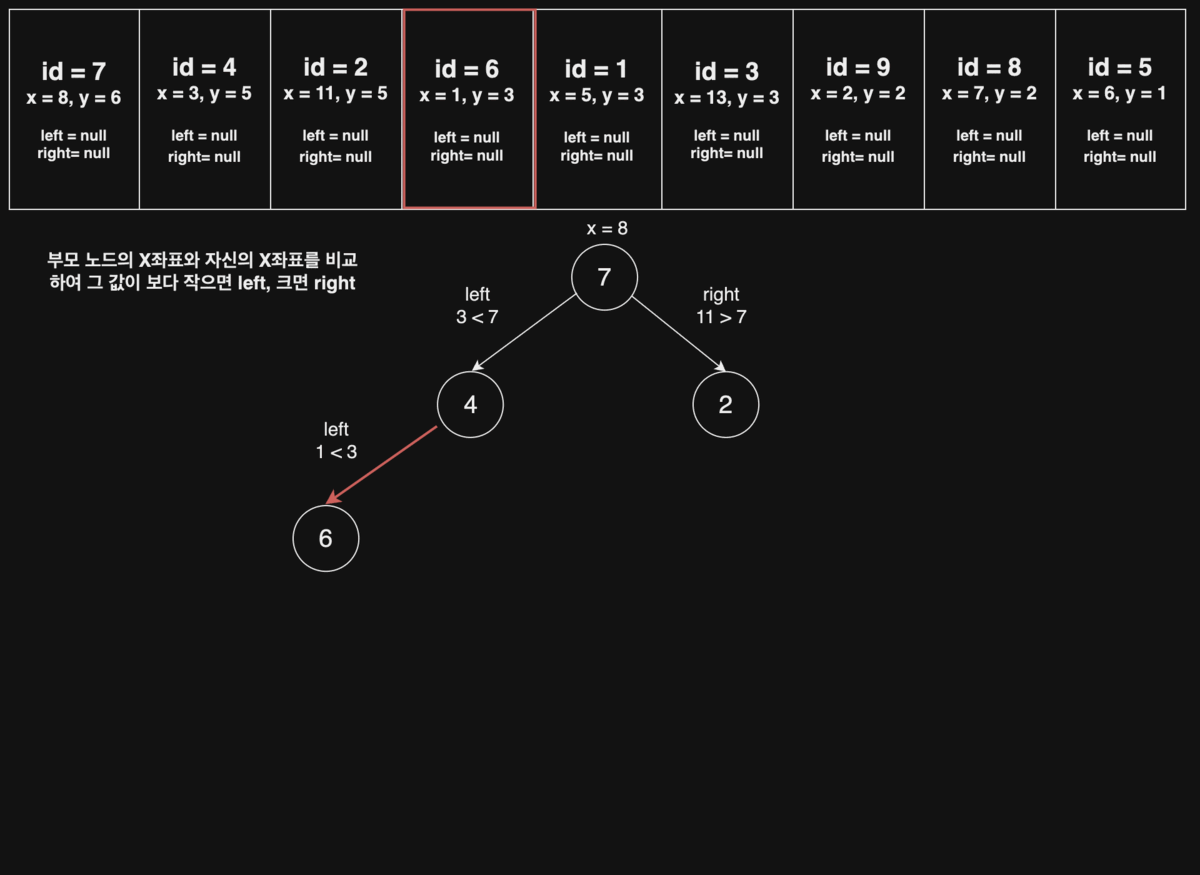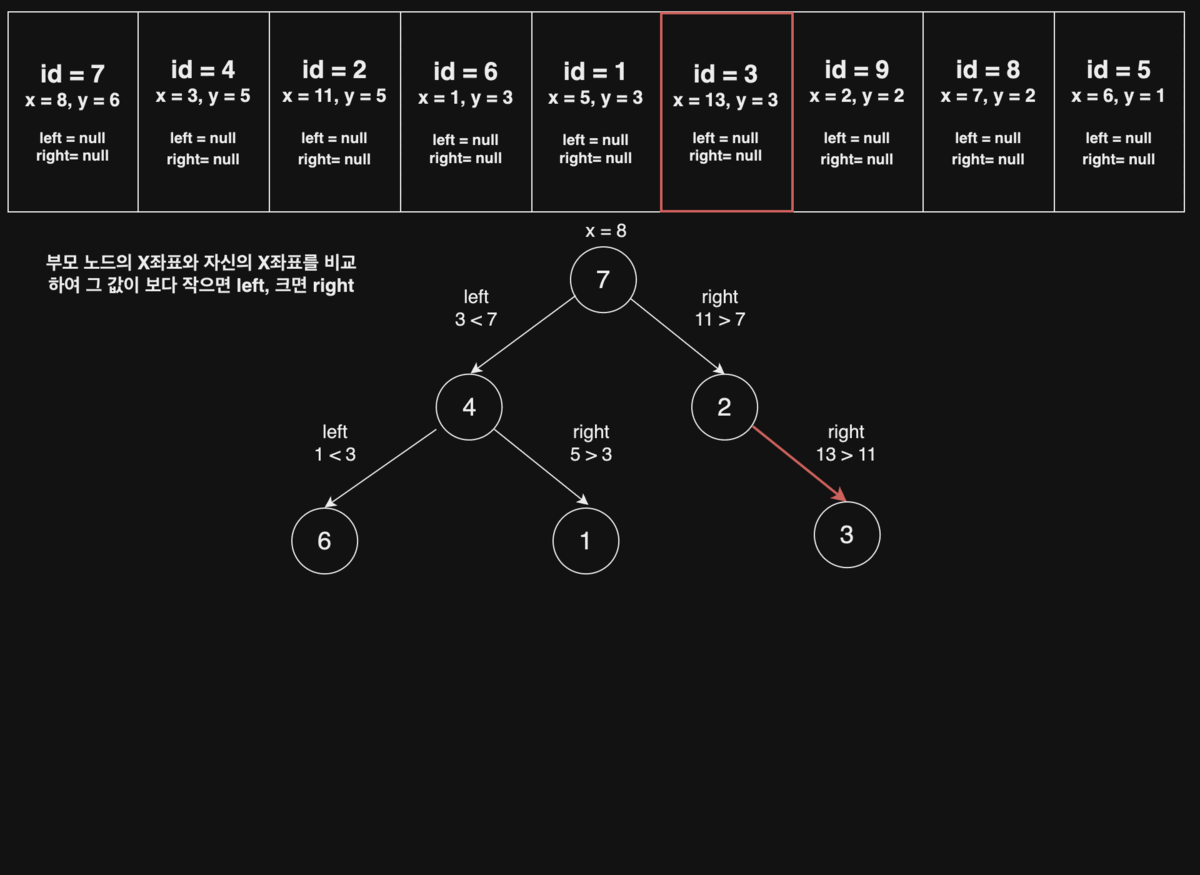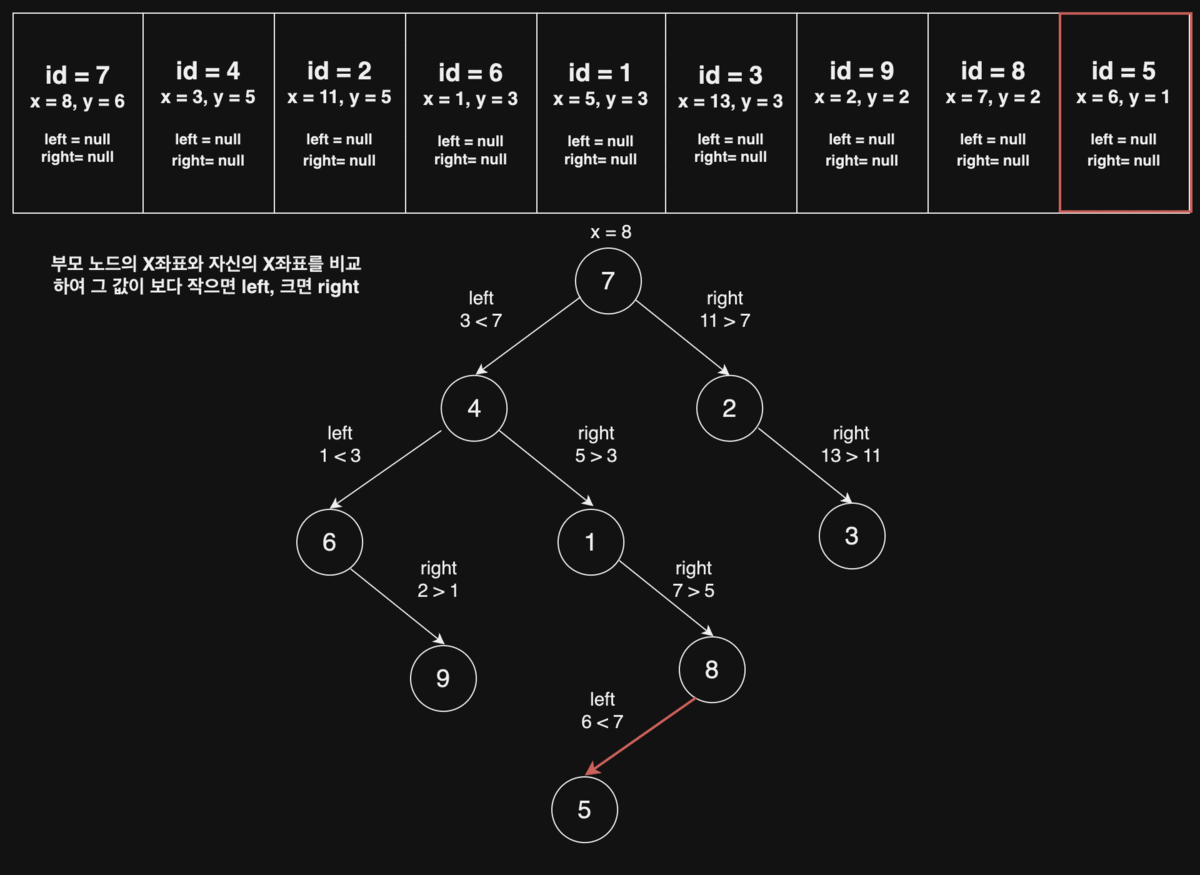
이진 트리를 구성하기 위해 노드의 y좌표는 내림차순으로 y좌표가 같다면, x좌표는 오름차순으로 정렬

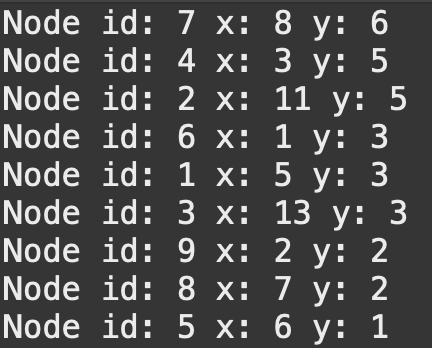
id = 7 를 Root Node라 할 때, 다음 오는 id = 4의 x좌표는 그 부모 노드(id = 7)의 x좌표 8보다 왼쪽에 존재, id = 2는 그 부모 노드(id = 7) x좌표 8보다 오른쪽에 존재하는 규칙을 찾을 수 있다.

Node 클래스 정의

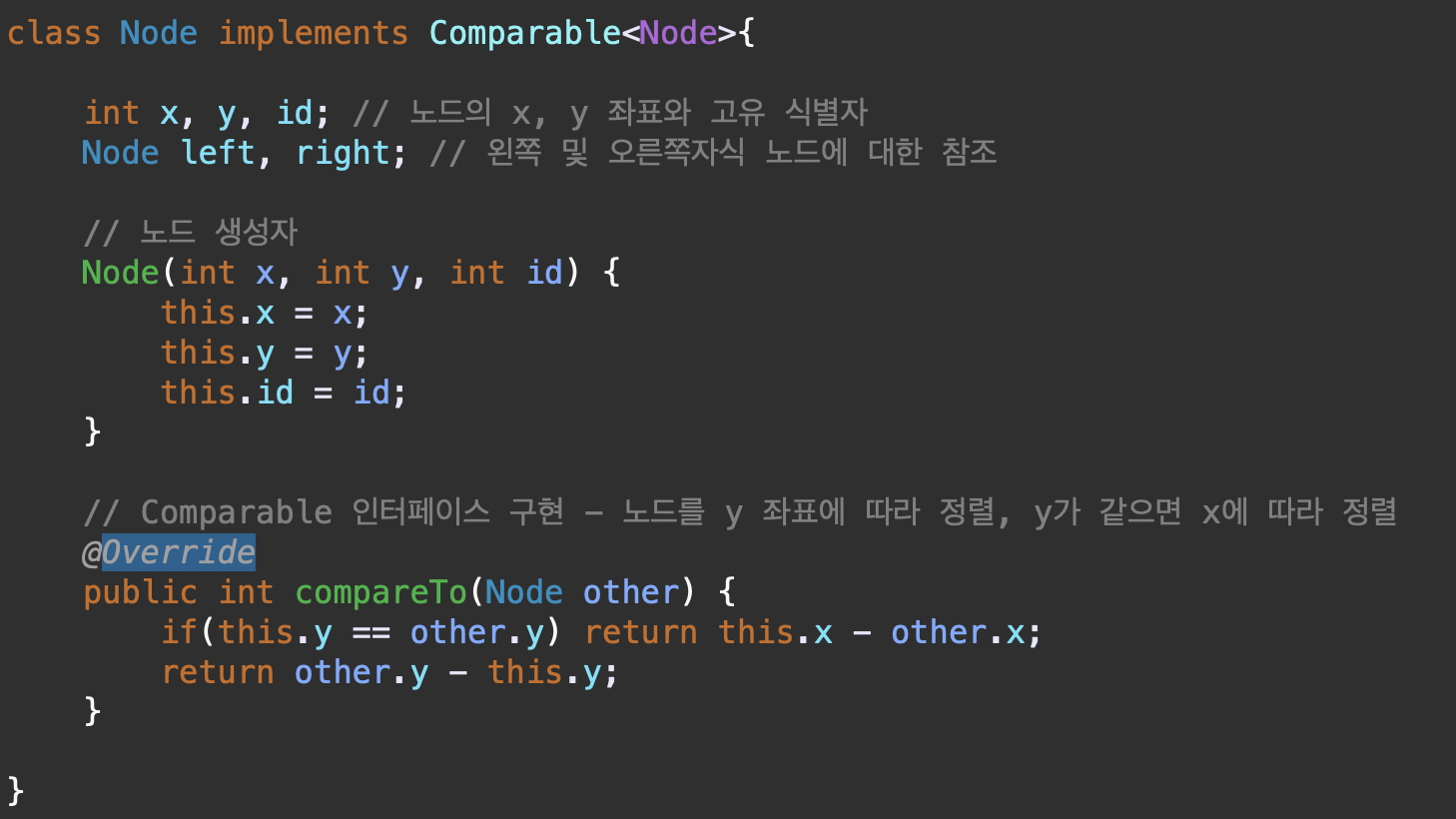
클래스 변수 정의

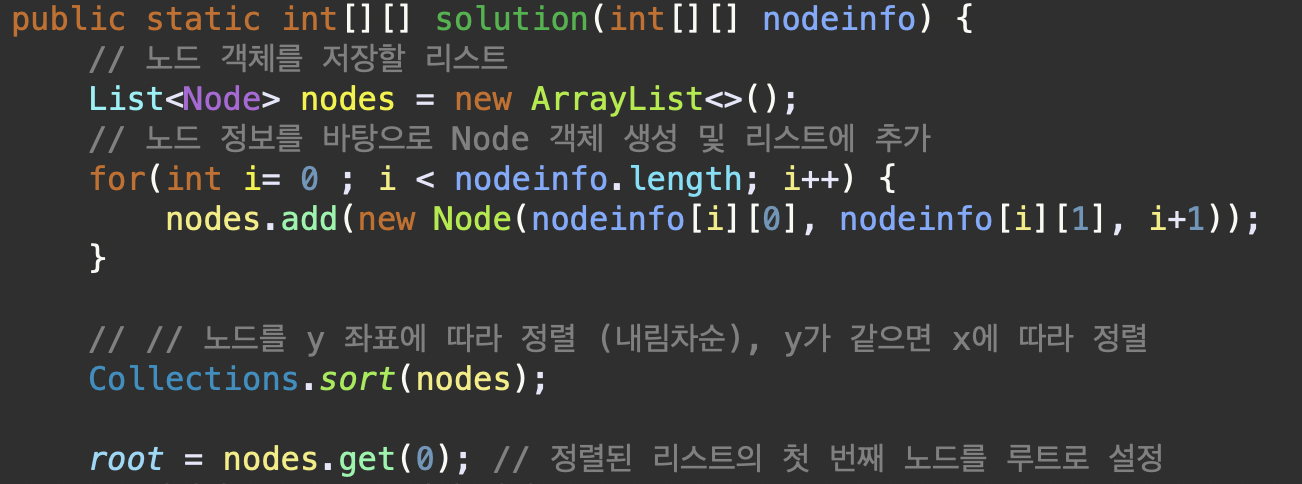
nodeinfo를 인자로 받아, 각 노드의 정보를 Node 객체로 변환하여 nodes 리스트에 추가한다. 이후, Collections.sort 메서드를 사용하여 Node 객체들을 compareTo 메서드에서 정의된 규칙에 따라 정렬한다.
👉🏻 여기서 정렬 규칙은 y좌표에 대해서는 내림차순, y좌표가 같은 경우 x 좌표에 대해서는 오름차순이다.

root Node에 나머지 노드들을 트리에 삽입

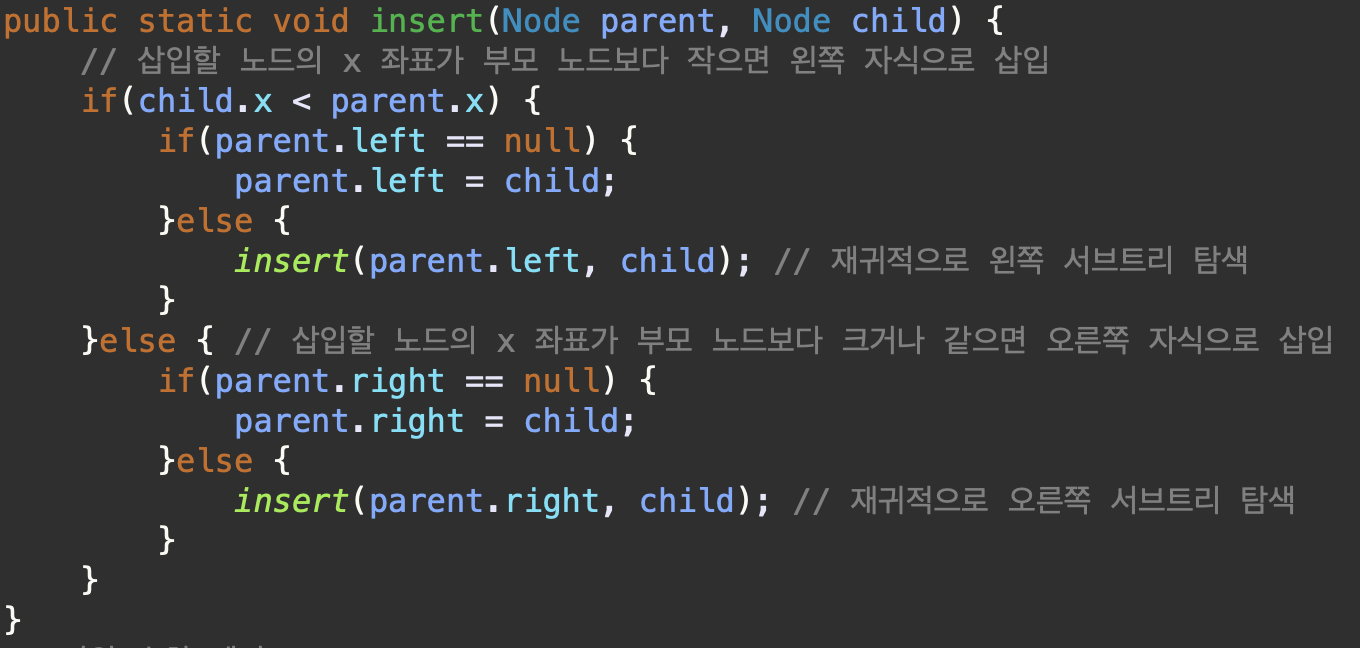
insert 메서드

전위, 후위 순회 함수 호출

전위 순회 찾기 메서드 구현

Root → left sub Tree → right sub Tree

후위 순회 찾기 메서드 구현

left sub Tree → right sub Tree → Root

전위, 후위 리스트를 2차원 answer 배열에 담기

최종 결과

---