Programmers #59

이강용·2024년 2월 27일

Programmers

목록 보기

58/58

`기둥과 보 설치`

문1) 빙하가 깨지면서 스노우타운에 떠내려 온 "죠르디"는 인생 2막을 위해 주택 건축사업에 뛰어들기로 결심하였습니다. "죠르디"는 기둥과 보를 이용하여 벽면 구조물을 자동으로 세우는 로봇을 개발할 계획인데, 그에 앞서 로봇의 동작을 시뮬레이션 할 수 있는 프로그램을 만들고 있습니다.
프로그램은 2차원 가상 벽면에 기둥과 보를 이용한 구조물을 설치할 수 있는데, 기둥과 보는 길이가 1인 선분으로 표현되며 다음과 같은 규칙을 가지고 있습니다.

기둥은 바닥 위에 있거나 보의 한쪽 끝 부분 위에 있거나, 또는 다른 기둥 위에 있어야 합니다.
보는 한쪽 끝 부분이 기둥 위에 있거나, 또는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 합니다.

단, 바닥은 벽면의 맨 아래 지면을 말합니다.

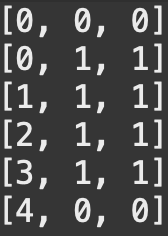
2차원 벽면은 n x n 크기 정사각 격자 형태이며, 각 격자는 1 x 1 크기입니다. 맨 처음 벽면은 비어있는 상태입니다. 기둥과 보는 격자선의 교차점에 걸치지 않고, 격자 칸의 각 변에 정확히 일치하도록 설치할 수 있습니다. 다음은 기둥과 보를 설치해 구조물을 만든 예시입니다.

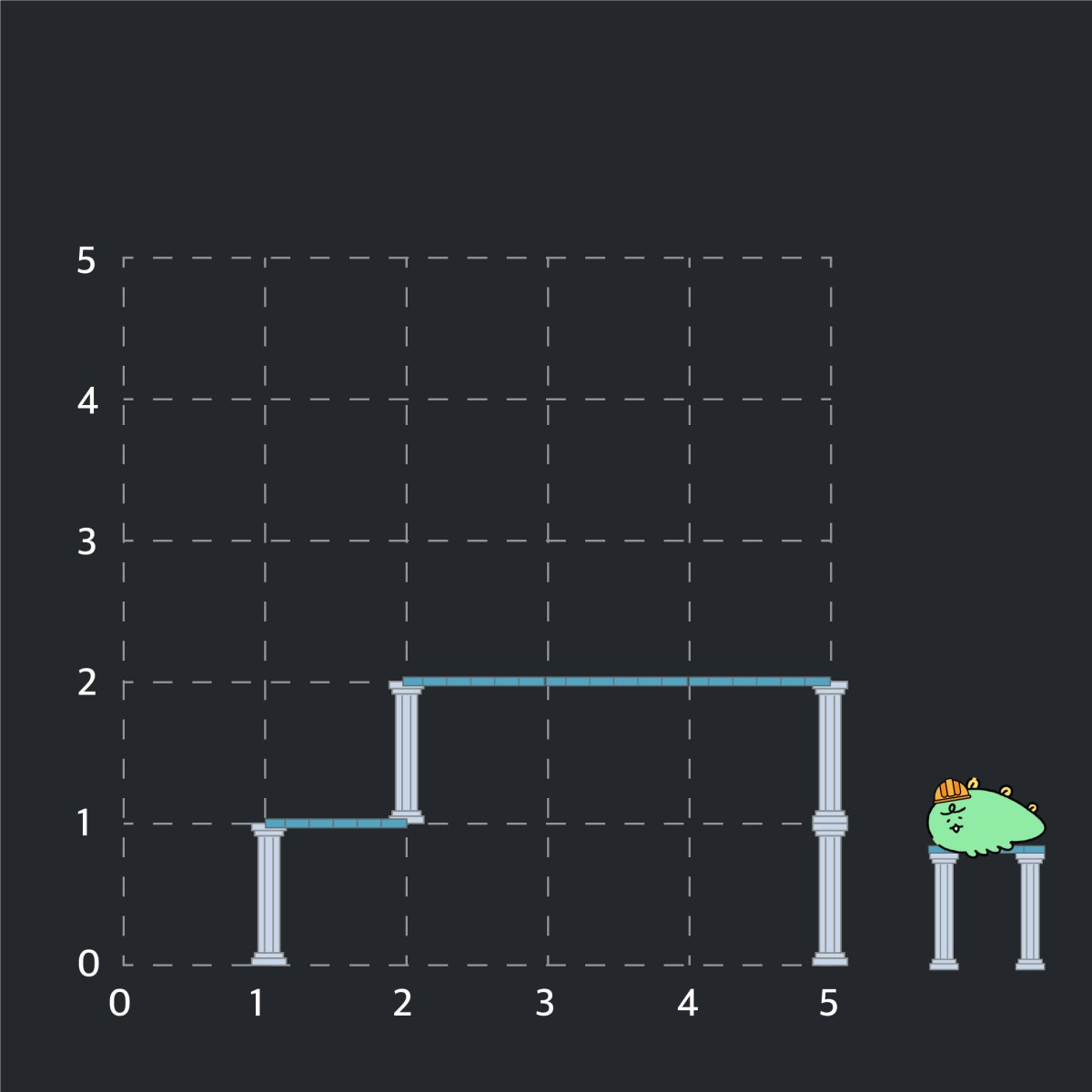
예를 들어, 위 그림은 다음 순서에 따라 구조물을 만들었습니다.

(1, 0)에서 위쪽으로 기둥을 하나 설치 후, (1, 1)에서 오른쪽으로 보를 하나 만듭니다.
(2, 1)에서 위쪽으로 기둥을 하나 설치 후, (2, 2)에서 오른쪽으로 보를 하나 만듭니다.
(5, 0)에서 위쪽으로 기둥을 하나 설치 후, (5, 1)에서 위쪽으로 기둥을 하나 더 설치합니다.
(4, 2)에서 오른쪽으로 보를 설치 후, (3, 2)에서 오른쪽으로 보를 설치합니다.

만약 (4, 2)에서 오른쪽으로 보를 먼저 설치하지 않고, (3, 2)에서 오른쪽으로 보를 설치하려 한다면 2번 규칙에 맞지 않으므로 설치가 되지 않습니다. 기둥과 보를 삭제하는 기능도 있는데 기둥과 보를 삭제한 후에 남은 기둥과 보들 또한 위 규칙을 만족해야 합니다. 만약, 작업을 수행한 결과가 조건을 만족하지 않는다면 해당 작업은 무시됩니다.

벽면의 크기 n, 기둥과 보를 설치하거나 삭제하는 작업이 순서대로 담긴 2차원 배열 build_frame이 매개변수로 주어질 때, 모든 명령어를 수행한 후 구조물의 상태를 return 하도록 solution 함수를 완성해주세요.

제한 사항

n은 5 이상 100 이하인 자연수입니다.
build_frame의 세로(행) 길이는 1 이상 1,000 이하입니다.
build_frame의 가로(열) 길이는 4입니다.
build_frame의 원소는 [x, y, a, b]형태입니다.
- x, y는 기둥, 보를 설치 또는 삭제할 교차점의 좌표이며, [가로 좌표, 세로 좌표] 형태입니다.
- a는 설치 또는 삭제할 구조물의 종류를 나타내며, 0은 기둥, 1은 보를 나타냅니다.
- b는 구조물을 설치할 지, 혹은 삭제할 지를 나타내며 0은 삭제, 1은 설치를 나타냅니다.
- 벽면을 벗어나게 기둥, 보를 설치하는 경우는 없습니다.
- 바닥에 보를 설치 하는 경우는 없습니다.
구조물은 교차점 좌표를 기준으로 보는 오른쪽, 기둥은 위쪽 방향으로 설치 또는 삭제합니다.
구조물이 겹치도록 설치하는 경우와, 없는 구조물을 삭제하는 경우는 입력으로 주어지지 않습니다.
최종 구조물의 상태는 아래 규칙에 맞춰 return 해주세요.
- return 하는 배열은 가로(열) 길이가 3인 2차원 배열로, 각 구조물의 좌표를 담고있어야 합니다.
- return 하는 배열의 원소는 [x, y, a] 형식입니다.
- x, y는 기둥, 보의 교차점 좌표이며, [가로 좌표, 세로 좌표] 형태입니다.
- 기둥, 보는 교차점 좌표를 기준으로 오른쪽, 또는 위쪽 방향으로 설치되어 있음을 나타냅니다.
- a는 구조물의 종류를 나타내며, 0은 기둥, 1은 보를 나타냅니다.
- return 하는 배열은 x좌표 기준으로 오름차순 정렬하며, x좌표가 같을 경우 y좌표 기준으로 오름차순 정렬해주세요.
- x, y좌표가 모두 같은 경우 기둥이 보보다 앞에 오면 됩니다.

입출력 예

n	build_frame	result
5	`[[1,0,0,1],[1,1,1,1],[2,1,0,1],[2,2,1,1],[5,0,0,1],[5,1,0,1],[4,2,1,1],[3,2,1,1]]`	`[[1,0,0],[1,1,1],[2,1,0],[2,2,1],[3,2,1],[4,2,1],[5,0,0],[5,1,0]]`
5	`[[0,0,0,1],[2,0,0,1],[4,0,0,1],[0,1,1,1],[1,1,1,1],[2,1,1,1],[3,1,1,1],[2,0,0,0],[1,1,1,0],[2,2,0,1]]`	`[[0,0,0],[0,1,1],[1,1,1],[2,1,1],[3,1,1],[4,0,0]]`

입출력 예 설명

입출력 예 #2

여덟 번째 작업을 수행 후 아래와 같은 구조물 만들어집니다.

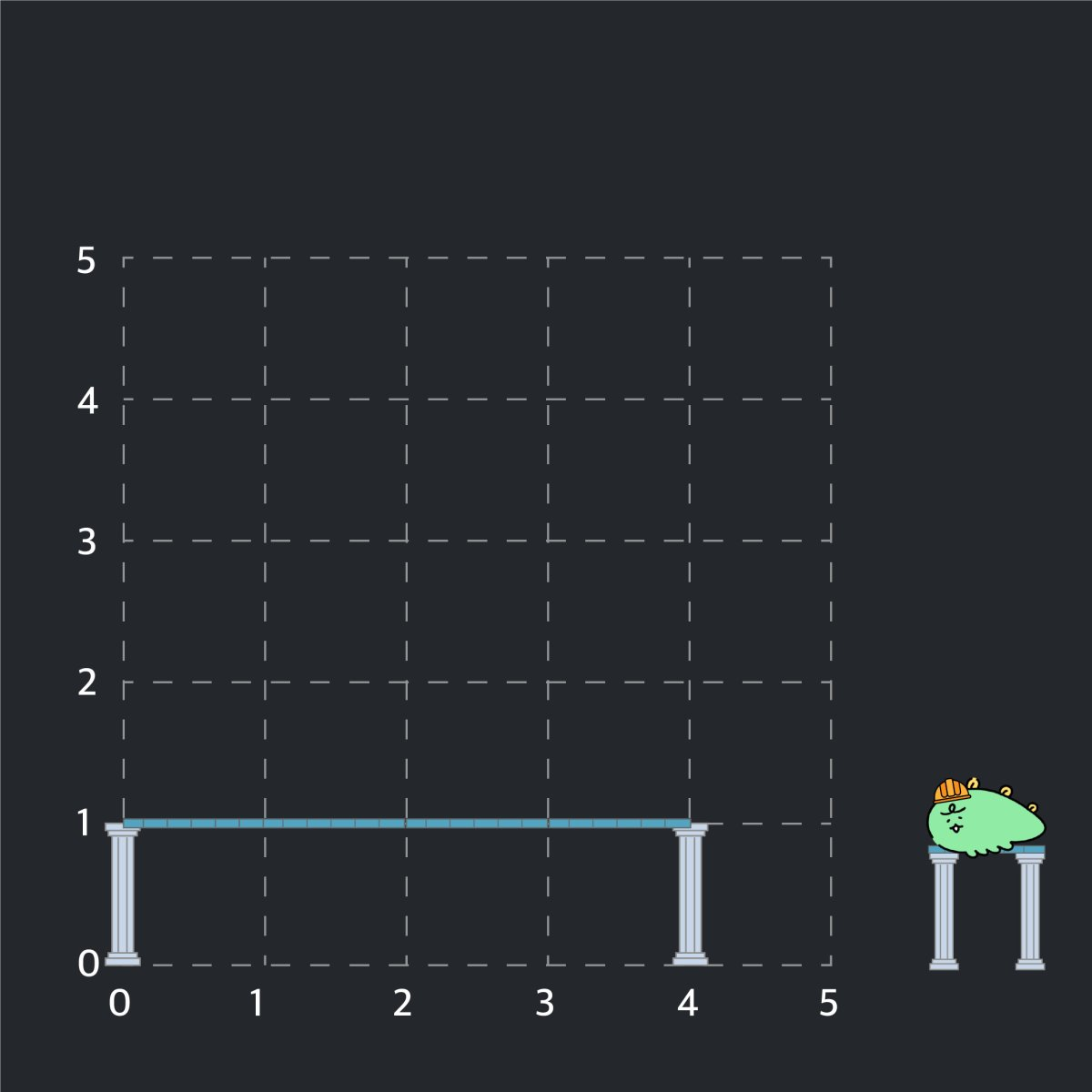
아홉 번째 작업의 경우, (1, 1)에서 오른쪽에 있는 보를 삭제하면 (2, 1)에서 오른쪽에 있는 보는 조건을 만족하지 않으므로 무시됩니다.

열 번째 작업의 경우, (2, 2)에서 위쪽 방향으로 기둥을 세울 경우 조건을 만족하지 않으므로 무시됩니다.

나의 풀이

import java.util.*;
class Solution {
     static Set<Build> structures = new HashSet<>();
	
	 static class Build{
		int x;
		int y;
		int type; // 0 for column, 1 for beam
	
		
		public Build(int x, int y, int type) {
			this.x = x;
			this.y = y;
			this.type = type;
		}
		
		
		@Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Build build = (Build) o;
            return x == build.x && y == build.y && type == build.type;
        }

        @Override
        public int hashCode() {
            return (31 * x + y) * 31 + type;
        }
	}
	 
	
	 public static boolean existsColumn(int x, int y) {
	     return structures.contains(new Build(x, y, 0));
	 }

	 public static boolean existsBeam(int x, int y) {
	     return structures.contains(new Build(x, y, 1));
	 }

	 public static boolean canPlaceBuild(Build build) {
	     if (build.type == 0) { 
	        
	         if (build.y == 0) return true;
	       
	         if (existsBeam(build.x - 1, build.y) || existsBeam(build.x, build.y)) return true;
	        
	         if (existsColumn(build.x, build.y - 1)) return true;
	     } else { 
	      
	         if (existsColumn(build.x, build.y - 1) || existsColumn(build.x + 1, build.y - 1)) return true;
	         
	         if (existsBeam(build.x - 1, build.y) && existsBeam(build.x + 1, build.y)) return true;
	     }
	     return false;
	 }

	 public static boolean canRemoveBuild(Build build) {
	    
	     structures.remove(build);
	     
	    
	     for (Build otherBuild : structures) {
	         if (!canPlaceBuild(otherBuild)) {
	            
	             structures.add(build);
	             return false;
	         }
	     }
	     
	     return true;
	 }
	
	public static int[][] solution(int n, int[][] build_frame) {
       
        for(int[] frame : build_frame) {
        	Build build = new Build(frame[0], frame[1], frame[2]);
        	
        	if(frame[3] == 1) { 
        		if(canPlaceBuild(build)) {
        			structures.add(build);
        		}
        	}else { 
        		if(canRemoveBuild(build)) {
        			structures.remove(build);
        		}
        	}
        }
        
        int[][] answer = new int[structures.size()][3];
        int index = 0;
        for (Build build : structures) {
            answer[index][0] = build.x;
            answer[index][1] = build.y;
            answer[index][2] = build.type;
            index++;
        }
        
        Arrays.sort(answer, (a, b) -> {
            if (a[0] != b[0])
                return Integer.compare(a[0], b[0]);
            else if (a[1] != b[1])
                return Integer.compare(a[1], b[1]);
            else
                return Integer.compare(a[2], b[2]);
        });
        
        return answer;
    }
}

2차원 배열로 푼 로직


package programmers;

public class ColumnAndBeamInstallation {
	
	
	static boolean[][] column;
	static boolean[][] beam;
	
	
	public static boolean checkColumn(int x, int y) {
		if(y == 0 || column[x][y-1]) return true; // 지면 위에 
		
		//현재 x좌표 이전(x-1)에 보가 있는지 또는 현재 x좌표에 보가 있는지
		if((x > 0 && beam[x-1][y]) || beam[x][y]) return true; 
		
		
		return false;
				
	}
	
	public static boolean checkBeam(int x, int y) {
		// 현재 x, y-1 좌표에 기둥이 있는 경우, 현재 x+1, y-1 좌표에 기둥이 있는 경우
		if(column[x][y-1] || column[x+1][y-1]) return true;
		
		// 양쪽에 보가 있는 경우
		if(x > 0 && beam[x-1][y] && beam[x+1][y]) return true;
		
		return false;
	}
	
	public static boolean canDelete(int x, int y) {
		for(int i = Math.max(x - 1, 0); i <= x + 1; i++) {
			for(int j = y; j <= y + 1; j++) {
				if(column[i][j] && !checkColumn(i, j)) {
					return false;
				}
				if(beam[i][j] && !checkBeam(i, j)) {
					return false;
				}
			}
		}
		
		return true;
	}
	
	public static int[][] solution(int n, int[][] build_frame) {
       
		column = new boolean[n+2][n+2];
		beam = new boolean[n+2][n+2];
        
		int count = 0;
		for(int[] build : build_frame) {
			int x = build[0];
			int y = build[1];
			int type = build[2];
			int cmd = build[3];
			
			
			if(type == 0) { // column
				if(cmd == 1) { // 설치
					if(checkColumn(x,y)) {
						column[x][y] = true;
						count++;
					}
				}else { // 삭제
					column[x][y] = false;
					if(!canDelete(x,y)) {
						column[x][y] = true;
					}else {
						count--;
					}
				}
				
			}else { // beam
				if(cmd == 1) {
					if(checkBeam(x,y)) {
						beam[x][y] = true;
						count++;
					}
				}else { // 삭제
					beam[x][y] = false;
					if(!canDelete(x,y)) {
						beam[x][y] = true;
							
					}else {
						count--;
					}
				}					
				
			}
		}
			
		
		
		int[][] answer = new int[count][3];
		count = 0;
		
		
		
		for(int x = 0; x <= n; x++) {
			for(int y = 0; y <= n; y++) {
				if(column[x][y]) {
					answer[count][0] = x;
					answer[count][1] = y;
					answer[count++][2] = 0;
				}
				if(beam[x][y]) {
					answer[count][0] = x;
					answer[count][1] = y;
					answer[count++][2] = 1;
				}
			}
		}

		
        return answer;
    }
	
	public static void main(String[] args) {
		
		
		
		int[][] build_frame = {{0,0,0,1},{2,0,0,1},{4,0,0,1},{0,1,1,1},{1,1,1,1},
				{2,1,1,1},{3,1,1,1},{2,0,0,0},{1,1,1,0},{2,2,0,1}
		};
		
		solution(5, build_frame);
	}

}

나의 생각

문제를 보며 가장 먼저 들었던 생각은 2차원 배열로 기둥과 보를 줬다는건 위 문제도 2차원 배열로 풀 수 있지않을까 생각하였다. 틀에 박힌 생각으로 2차원 배열의 크기를 키울 생각을 못했던게 이번 문제의 포인트를 놓치지않았을까 라는 생각이 들었다. 아래 그림처럼 2차원 배열 크기를 n보다 + 1 만큼 사이즈를 키워 기둥과 보 모두가 2차원 배열안에 놓이도록 하는게 핵심이였던것같다.

n+1 만큼 배열 크기를 설정, 기둥 배열과 보 배열을 개별로 선언

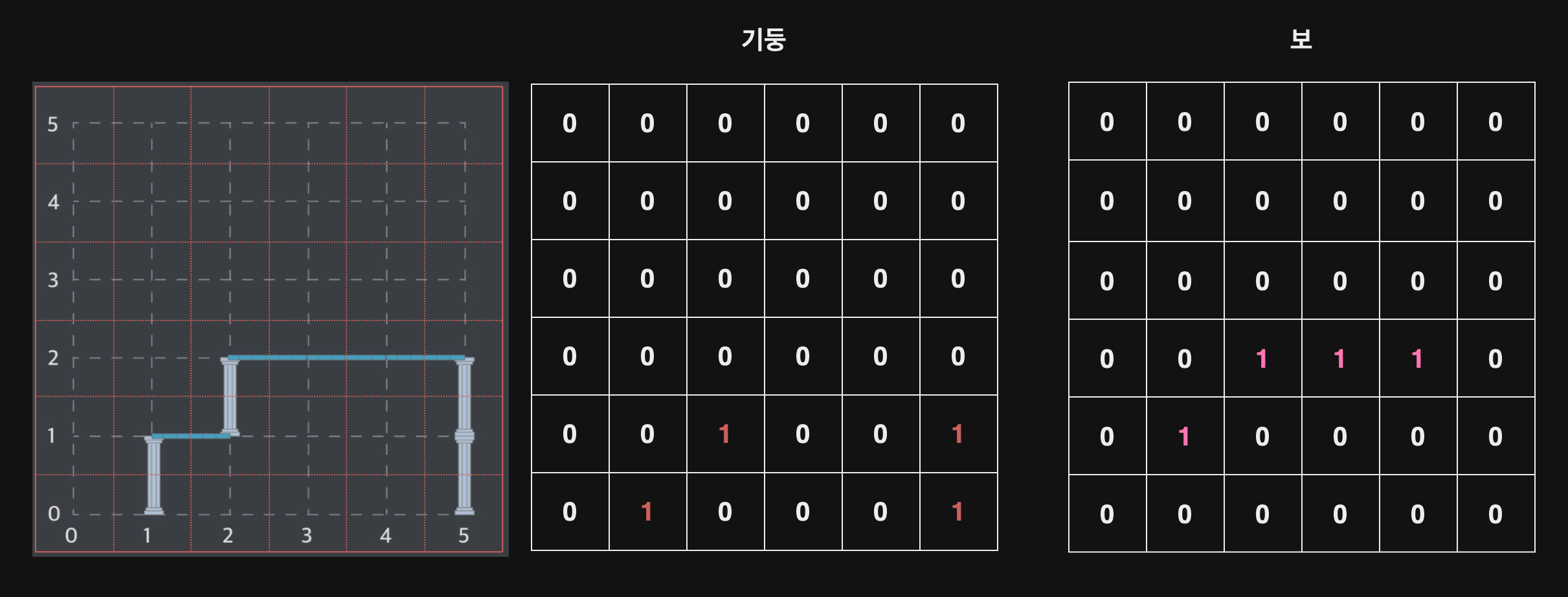
문제의 조건

기둥은 바닥 위에 있거나 보의 한쪽 끝 부분 위에 있거나, 또는 다른 기둥 위에 있어야 합니다.
보는 한쪽 끝 부분이 기둥 위에 있거나, 또는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 합니다.

위 그림 및 문제의 조건을 보면 몇 가지 특징을 알 수 있다.
y = 0일때 기둥은 존재할 수 있다.
기둥 위에 기둥이 존재할 수 있다.
기둥 위에 보가 존재할 수 있다.
보 한쪽 끝에 기둥이 존재할 수 있다.
보와 보 사이에 보가 존재할 수 있다.

`column & beam 정적 변수 선언`

`배열 크기 할당 (n+2)`

👉🏻 처음 로직을 구성할 때 n+1로 크기를 정했지만, 추후 반복문에서 배열의 범위를 초과할 수 있는 문제가 발생할 수 있으므로 이를 미연에 방지하는 목적으로 배열의 크기를 n + 2로 할당

`매개변수 build_frame 순회 및 변수 초기화`

x,y 좌표, type (0 : 기둥, 1: 보) 그리고 cmd(0: 삭제, 1: 설치)

`핵심 로직 #1`

type == 0은 build_frame를 순회하면서 기둥이 나올 때를 검출하는 로직으로
기둥이면서 설치 또는 삭제 인지를 판별한다.

`checkColumn()`

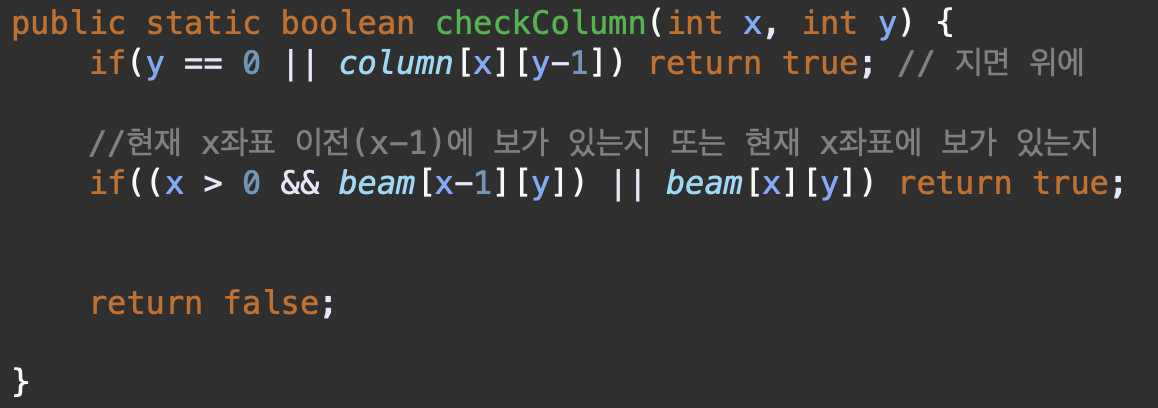
지면 위(y = 0)이나 기둥위에 기둥이 있을 경우( column[x][y-1])
현재 x좌표 이전(x-1)에 보가 있는지 또는 현재 x좌표에 보가 있는지

cmd == 1면서, checkColumn이 true 이면 2차원 column 배열 해당 좌표에 true로 할당

`핵심 로직 #2`

type == 1은 build_frame를 순회하면서 보가 나올 때를 검출하는 로직으로
보이면서 설치 또는 삭제 인지를 판별한다.

`checkBeam()`

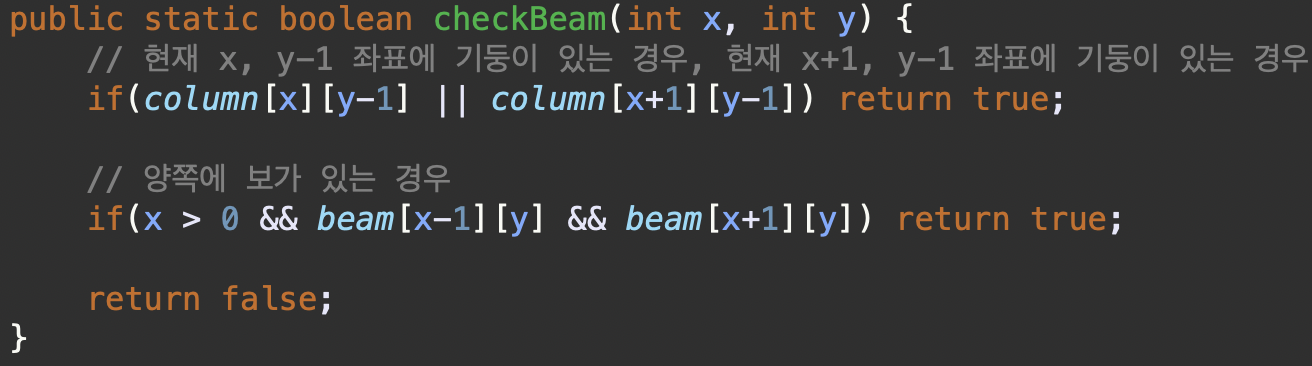
현재 좌표(x,y)를 기준으로 보의 왼쪽, 오른쪽 끝 부분이 기둥 위에 있는지 확인
양옆에 보가 있는 경우 보가 존재할 수 있다.

`canDelete()`

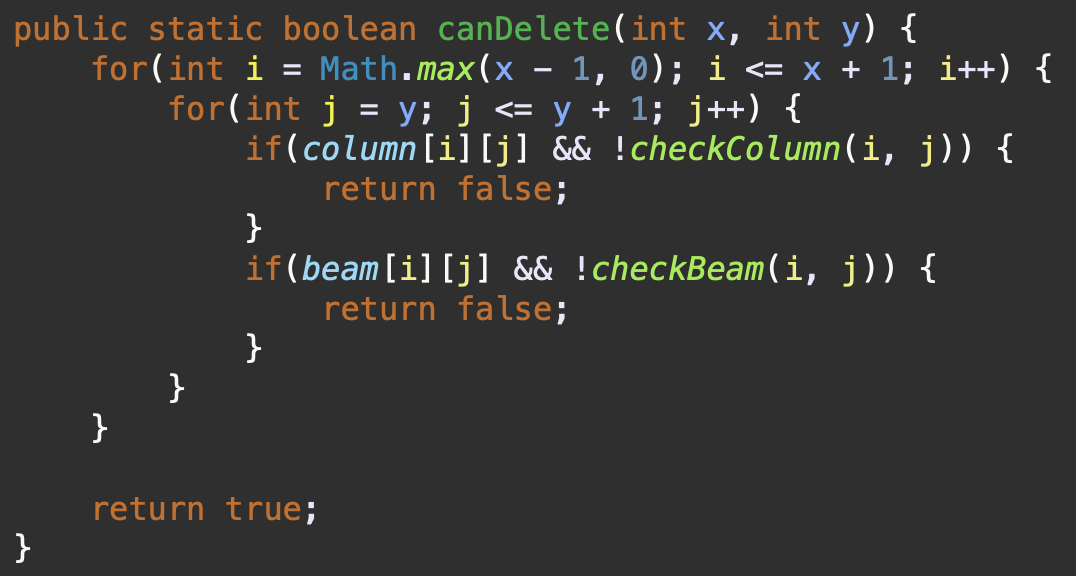
주어진 x,y 좌표에 있는 구조물을 삭제할 수 있는지 검사하는 로직으로, 삭제하려는 구조물의 x,y 좌표 기준으로 주변 6개의 격자 칸을 확인하면 된다.

(x - 1, y)

(x, y)

(x + 1, y)

(x - 1, y + 1)

(x, y + 1)

(x + 1, y + 1)

기둥(column)의 경우

기둥은 바닥(y = 0) 위에 있거나 다른 기둥 위에 있어야 한다.

기둥의 한쪽 끝 부분이 어떤 보의 한쪽 끝 부분 위에 있어야 한다.

보(beam)의 경우

보의 한쪽 끝 부분이 기둥 위에 있어야 한다.

보는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 한다.

삭제 과정

삭제 시도 : 우선, column[x][y] = false; 또는 beam[x][y] = false; 를 통해 기둥이나 보를 격자에서 제거한다. 이는 코드 상에서 해당 구조물의 존재 여부를 표시하는 배열의 값을 변경하는 것으로, 실제 구조물을 제거한 것 처럼 표시

주변 구조 안정성 확인 : 이후 canDelete(x,y) 함수를 호출하여 기둥이나 보를 제거했을 때 주변 구조물들이 안정적으로 설치되어 있는지 확인. 함수는 주변 6개의 격자 칸에 대해 각 기둥과 보가 설치 규칙을 만족하는지 검사

기둥 확인 : if(column[i][j] && !checkColumn(i, j)) 조건을 통해 주변에 있는 기둥들이 격자에 남아 있는 경우, 그 기둥이 설치 규칙을 만족하는지 검사한다. 만약 설치 규칙을 만족하지 않는다면, 즉 기둥이 떠 있게 되면 false를 반환하여 삭제가 불가능함을 나타낸다.

보 확인 : if(beam[i][j] && !checkBeam(i, j)) 조건을 통해 주변에 있는 보들이 격자에 남아있는 경우, 그 보가 설치 규칙을 만족하는지 검사한다. 만약 설치 규칙을 만족하지 않는다면, 즉 보가 한쪽이나 양쪽 끝에서 지지를 받지 못한다면, false를 반환하여 삭제가 불가능함을 나타낸다.

결과 처리 : canDelete 함수의 결과에 따라 다음과 같이 처리한다.

canDelete에서 true를 반환하면, 삭제가 가능한 것으로 간주하고, 구조물의 삭제를 확정한다. 이 경우 count를 감소시켜 구조물의 총 개수를 업데이트한다.

canDelete에서 false를 반환하면, 삭제가 불가능한 것으로 간주하고, 원래의 column[x][y] = true; 또는 beam[x][y] = true;를 통해 구조물을 원상 복구한다.

`결과 반환`

여기서 count는 최종적으로 격자에 남아 있는 구조물의 총 개수를 나타내며 2차원 answer 배열의 행 크기를 의미한다.

Build 객체를 활용한 로직	2차원 배열 로직

`광고 삽입`

문2) 카카오TV에서 유명한 크리에이터로 활동 중인 죠르디는 환경 단체로부터 자신의 가장 인기있는 동영상에 지구온난화의 심각성을 알리기 위한 공익광고를 넣어 달라는 요청을 받았습니다. 평소에 환경 문제에 관심을 가지고 있던 "죠르디"는 요청을 받아들였고 광고효과를 높이기 위해 시청자들이 가장 많이 보는 구간에 공익광고를 넣으려고 합니다. "죠르디"는 시청자들이 해당 동영상의 어떤 구간을 재생했는 지 알 수 있는 재생구간 기록을 구했고, 해당 기록을 바탕으로 공익광고가 삽입될 최적의 위치를 고를 수 있었습니다.
참고로 광고는 재생 중인 동영상의 오른쪽 아래에서 원래 영상과 동시에 재생되는 PIP(Picture in Picture) 형태로 제공됩니다.

다음은 "죠르디"가 공익광고가 삽입될 최적의 위치를 고르는 과정을 그림으로 설명한 것입니다.

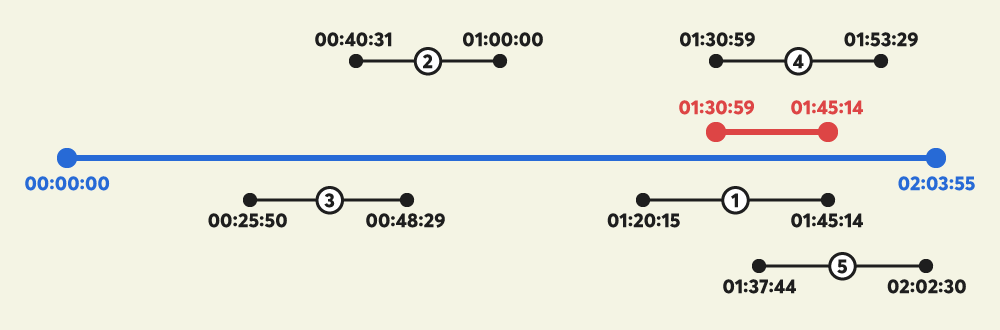
그림의 파란색 선은 광고를 검토 중인 "죠르디" 동영상의 전체 재생 구간을 나타냅니다.
- 위 그림에서, "죠르디" 동영상의 총 재생시간은 02시간 03분 55초 입니다.
그림의 검은색 선들은 각 시청자들이 "죠르디"의 동영상을 재생한 구간의 위치를 표시하고 있습니다.
- 검은색 선의 가운데 숫자는 각 재생 기록을 구분하는 ID를 나타냅니다.
- 검은색 선에 표기된 왼쪽 끝 숫자와 오른쪽 끝 숫자는 시청자들이 재생한 동영상 구간의 시작 시각과 종료 시각을 나타냅니다.
- 위 그림에서, 3번 재생 기록은 00시 25분 50초 부터 00시 48분 29초 까지 총 00시간 22분 39초 동안 죠르디의 동영상을 재생했습니다.
- 위 그림에서, 1번 재생 기록은 01시 20분 15초 부터 01시 45분 14초 까지 총 00시간 24분 59초 동안 죠르디의 동영상을 재생했습니다.
그림의 빨간색 선은 "죠르디"가 선택한 최적의 공익광고 위치를 나타냅니다.
- 만약 공익광고의 재생시간이 00시간 14분 15초라면, 위의 그림처럼 01시 30분 59초 부터 01시 45분 14초 까지 공익광고를 삽입하는 것이 가장 좋습니다. 이 구간을 시청한 시청자들의 누적 재생시간이 가장 크기 때문입니다.
- 01시 30분 59초 부터 01시 45분 14초 까지의 누적 재생시간은 다음과 같이 계산됩니다.
  - 01시 30분 59초 부터 01시 37분 44초 까지 : 4번, 1번 재생 기록이 두차례 있으므로 재생시간의 합은 00시간 06분 45초 X 2 = 00시간 13분 30초
  - 01시 37분 44초 부터 01시 45분 14초 까지 : 4번, 1번, 5번 재생 기록이 세차례 있으므로 재생시간의 합은 00시간 07분 30초 X 3 = 00시간 22분 30초
  - 따라서, 이 구간 시청자들의 누적 재생시간은 00시간 13분 30초 + 00시간 22분 30초 = 00시간 36분 00초입니다.

문제

"죠르디"의 동영상 재생시간 길이 play_time, 공익광고의 재생시간 길이 adv_time, 시청자들이 해당 동영상을 재생했던 구간 정보 logs가 매개변수로 주어질 때, 시청자들의 누적 재생시간이 가장 많이 나오는 곳에 공익광고를 삽입하려고 합니다. 이때, 공익광고가 들어갈 시작 시각을 구해서 return 하도록 solution 함수를 완성해주세요. 만약, 시청자들의 누적 재생시간이 가장 많은 곳이 여러 곳이라면, 그 중에서 가장 빠른 시작 시각을 return 하도록 합니다.

제한 사항

play_time, adv_time은 길이 8로 고정된 문자열입니다.
- play_time, adv_time은 HH:MM:SS 형식이며, 00:00:01 이상 99:59:59 이하입니다.
- 즉, 동영상 재생시간과 공익광고 재생시간은 00시간 00분 01초 이상 99시간 59분 59초 이하입니다.
- 공익광고 재생시간은 동영상 재생시간보다 짧거나 같게 주어집니다.
logs는 크기가 1 이상 300,000 이하인 문자열 배열입니다.
- logs 배열의 각 원소는 시청자의 재생 구간을 나타냅니다.
- logs 배열의 각 원소는 길이가 17로 고정된 문자열입니다.
- logs 배열의 각 원소는 H1:M1:S1-H2:M2:S2 형식입니다.
  - H1:M1:S1은 동영상이 시작된 시각, H2:M2:S2는 동영상이 종료된 시각을 나타냅니다.
  - H1:M1:S1는 H2:M2:S2보다 1초 이상 이전 시각으로 주어집니다.
  - H1:M1:S1와 H2:M2:S2는 play_time 이내의 시각입니다.
시간을 나타내는 HH, H1, H2의 범위는 00~99, 분을 나타내는 MM, M1, M2의 범위는 00~59, 초를 나타내는 SS, S1, S2의 범위는 00~59까지 사용됩니다. 잘못된 시각은 입력으로 주어지지 않습니다. (예: 04:60:24, 11:12:78, 123:12:45 등)
return 값의 형식
- 공익광고를 삽입할 시각을 HH:MM:SS 형식의 8자리 문자열로 반환합니다.

입출력 예

play_time	adv_time	logs	result
`"02:03:55"`	`"00:14:15"`	`["01:20:15-01:45:14", "00:40:31-01:00:00", "00:25:50-00:48:29", "01:30:59-01:53:29", "01:37:44-02:02:30"]`	`"01:30:59"`
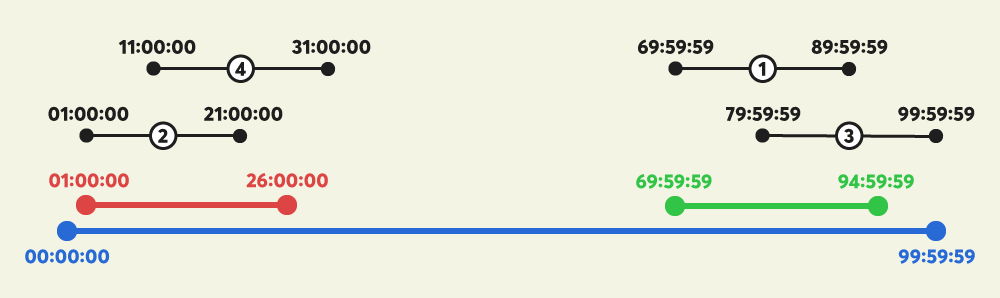
`"99:59:59"`	`"25:00:00"`	`["69:59:59-89:59:59", "01:00:00-21:00:00", "79:59:59-99:59:59", "11:00:00-31:00:00"]`	`"01:00:00"`
`"50:00:00"`	`"50:00:00"`	`["15:36:51-38:21:49", "10:14:18-15:36:51", "38:21:49-42:51:45"]`	`"00:00:00"`

입출력 예 설명

입출력 예 #2

01:00:00에 공익광고를 삽입하면 26:00:00까지 재생되며, 이곳이 가장 좋은 위치입니다. 이 구간의 시청자 누적 재생시간은 다음과 같습니다.

01:00:00-11:00:00 : 해당 구간이 1회(2번 기록) 재생되었으므로 누적 재생시간은 10시간 00분 00초 입니다.
11:00:00-21:00:00 : 해당 구간이 2회(2번, 4번 기록) 재생되었으므로 누적 재생시간은 20시간 00분 00초 입니다.
21:00:00-26:00:00 : 해당 구간이 1회(4번 기록) 재생되었으므로 누적 재생시간은 05시간 00분 00초 입니다.
따라서, 이 구간의 시청자 누적 재생시간은 10시간 00분 00초 + 20시간 00분 00초 + 05시간 00분 00초 = 35시간 00분 00초 입니다.
초록색으로 표시된 구간(69:59:59-94:59:59)에 광고를 삽입해도 동일한 결과를 얻을 수 있으나, 01:00:00이 69:59:59 보다 빠른 시각이므로, "01:00:00"을 return 합니다.

입출력 예 #3

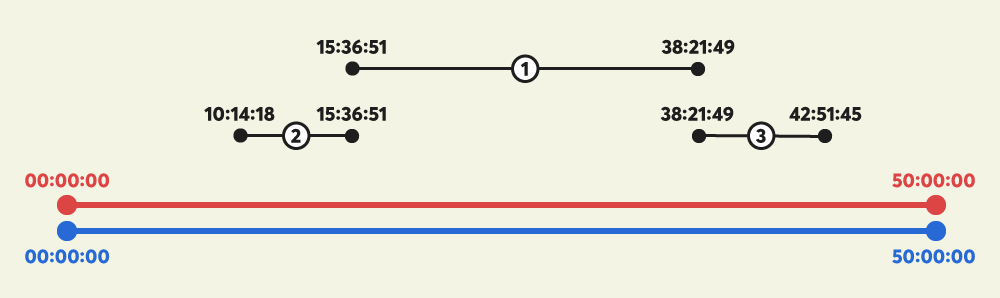
동영상 재생시간과 공익광고 재생시간이 같으므로, 삽입할 수 있는 위치는 맨 처음(00:00:00)이 유일합니다.

✓ 동영상 재생시간 = 재생이 종료된 시각 - 재생이 시작된 시각(예를 들어, 00시 00분 01초부터 00시 00분 10초까지 동영상이 재생되었다면, 동영상 재생시간은 9초 입니다.)

나의 풀이

package programmers;

public class InsertAdvertisement {
	
	
	
	public static int convert(String time) {
		
		String[] nums = time.split(":");
		
		return (Integer.parseInt(nums[0]) * 3600) + (Integer.parseInt(nums[1]) * 60) + Integer.parseInt(nums[2]);
	}
	
	
	public static String solution(String play_time, String adv_time, String[] logs) {
        
        
        int playSec = convert(play_time);
        int advSec = convert(adv_time);
        int[] totalSec = new int[100 * 3600];
        
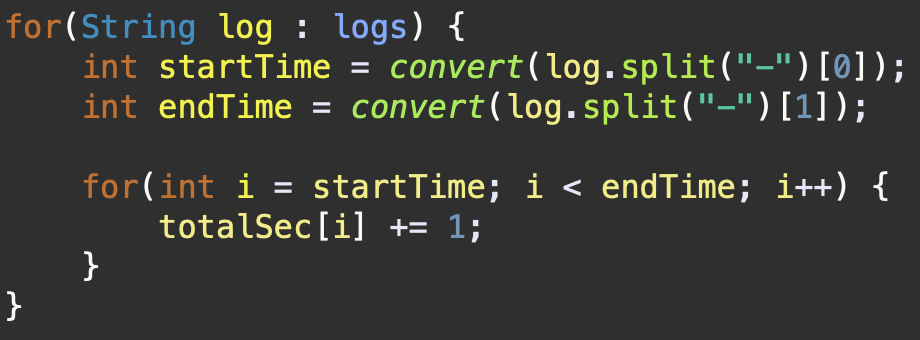
        for(String log : logs) {
        	int startTime = convert(log.split("-")[0]);
        	int endTime = convert(log.split("-")[1]);
        	
        	for(int i = startTime; i < endTime; i++) {
        		totalSec[i] += 1;
        	}
        }
        
        
        long cumulativeTimeSum = 0;
        
        for(int i = 0; i < advSec; i++) {
        	cumulativeTimeSum += totalSec[i];
        }
        
        long maxSum = cumulativeTimeSum;
        int maxIndex = 0;
        for(int i = advSec; i < playSec; i++) {
        	cumulativeTimeSum = cumulativeTimeSum + totalSec[i] - totalSec[i-advSec];
        	if(cumulativeTimeSum > maxSum) {
        		maxSum = cumulativeTimeSum;
        		maxIndex = i - advSec + 1;
        	}
        }
        
        
        System.out.println(String.format("%02d:%02d:%02d", maxIndex/3600, maxIndex/60 % 60, maxIndex % 60));
        
        return String.format("%02d:%02d:%02d", maxIndex/3600, maxIndex/60 % 60, maxIndex % 60);
    }
	
	
	public static void main(String[] args) {
		
		String[] logs = {"01:20:15-01:45:14", "00:40:31-01:00:00", "00:25:50-00:48:29", 
				"01:30:59-01:53:29", "01:37:44-02:02:30"};
		
		solution("02:03:55", "00:14:15", logs);
	}

}

나의 생각

매개변수로 주어지는 시간(HH:MM:SS)을 적절히 처리하는게 중요한 포인트였는데, 모든 시간을 초로 변환시키는 방법을 사용하였다. 예를들어, 01:20:15를 초로 변환하면 다음과 같다.

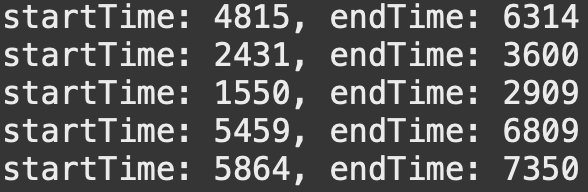
1 * 3600 + 20 * 60 + 15 = 3600 + 1200 + 15 = 4815초

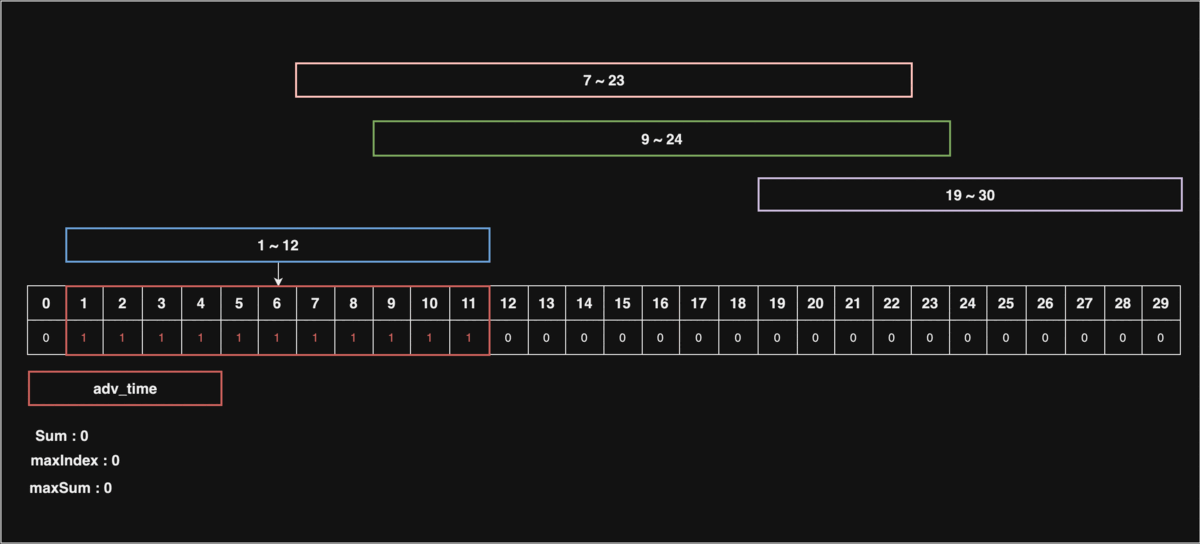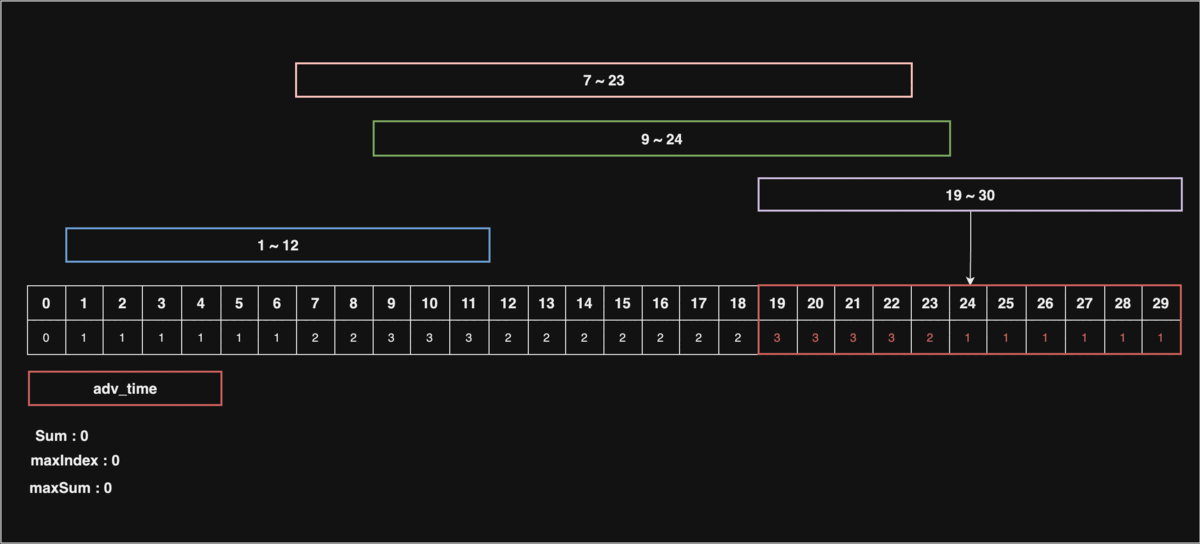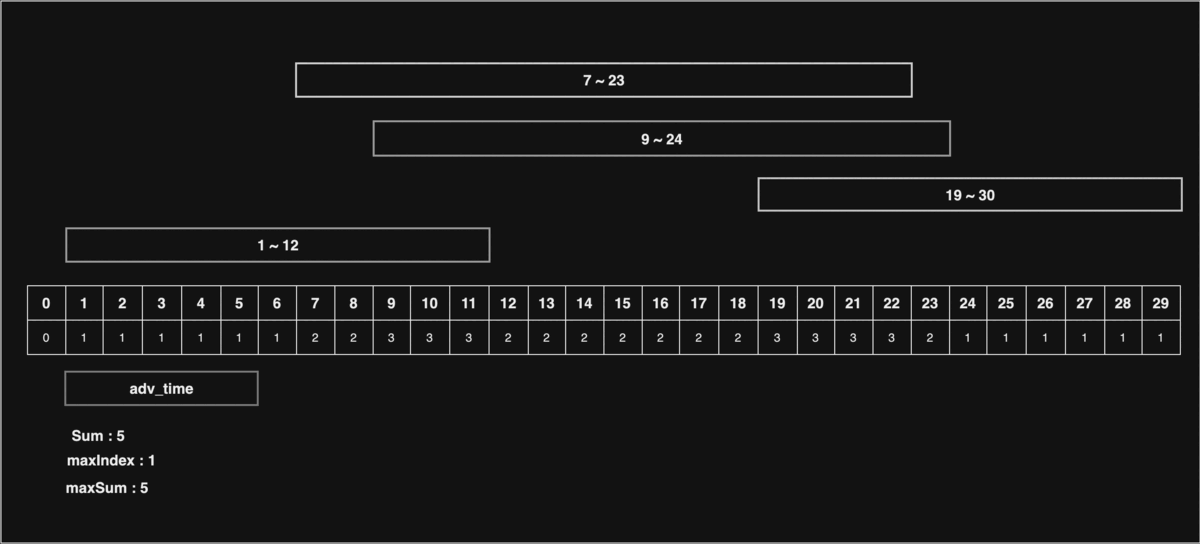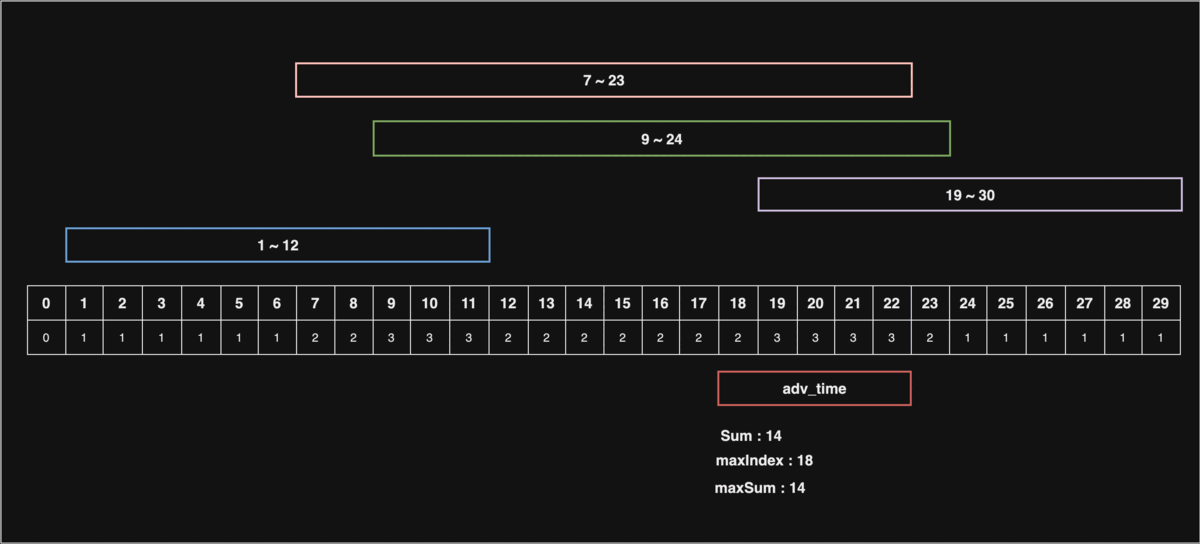
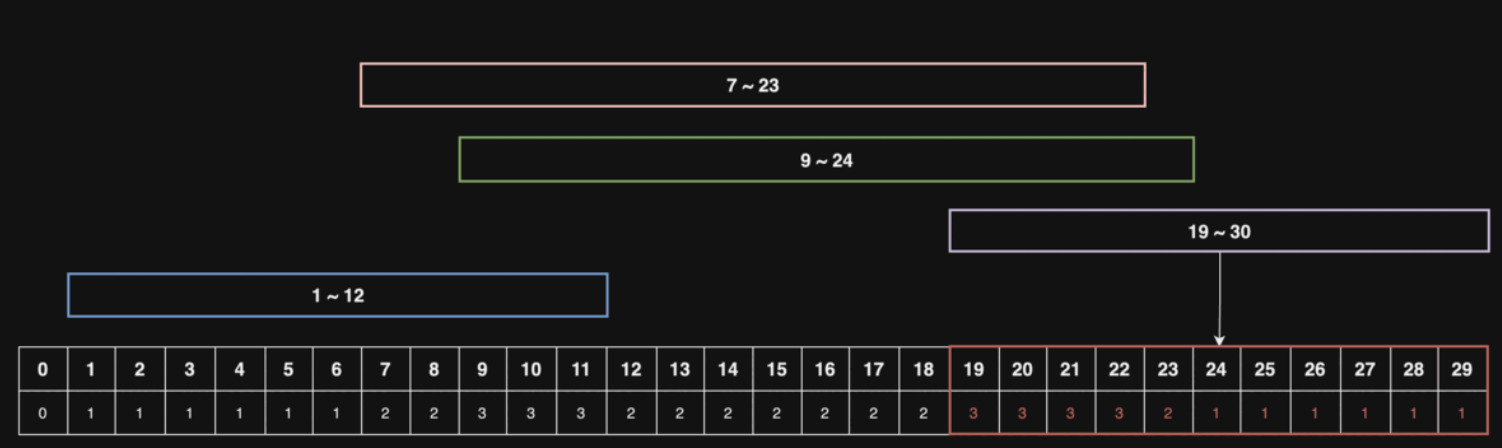
위 동적 이미지를 보면서 설명을 하자면, 만약 30초 상당의 동영상이 있다고 하자.

시청자들의 구간 정보를 1초 ~ 12초, 7초 ~ 23초, 9초 ~ 24초, 19초 ~ 30초로 나타내고, 구간을 모두 카운팅하여, 제일 많이 카운팅된 구간에서 공익광고를 재생한다면 가장 큰 효과를 낼 것이다.
전체 배열을 순회하며 공익광고 재생시간만큼 반복을 진행하여 구간별 누적 재생시간이 가장 많을 때의 index를 다시 시,분,초로 변환하여 리턴하면 된다.
위 동적 이미지에서는 18초 부터 22초까지(5초간) 재생해야 극대의 효과를 낼 수 있다.

위 내용을 정리하면 다음과 같다.
1. 시청자들의 시청 구간 정보를 통해 가장 많이 중첩되는 시간대를 찾고, 공익 광고를 삽입할 최적의 구간을 찾는다.
2. 전체 시청 구간에 걸쳐 각 초마다 몇 명의 시청자가 동영상을 시청하고 있는지의 누적 값을 계산한다. 이를 통해 가장 높은 시청자 수를 보이는 구간을 찾는다.
3. 공익광고의 재생 시간을 고려하여, 이 시간 동안 최대한 많은 시청자가 광고를 볼 수 있는 시작 지점(초)를 찾는다.

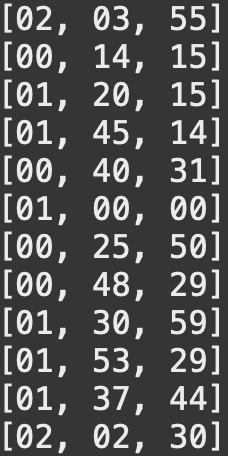
시,분,초 형식으로 된 시간 정보를 모두 초단위의 시간으로 변환하는 로직이다.

변환전 nums	변환 후 return 값

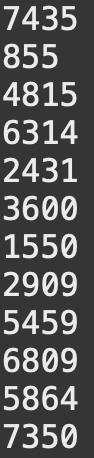totalSec 배열의 크기는 문제에서 시간의 범위를 0~99 시간으로 주어졌기때문에, 시간을 대략 100h * 3600 (시간(h) → 초(s))로 변환한 크기로 설정한다.

즉, 위 사진과 같이 4815 ~ 6314, 2431 ~ 3600, 1550 ~ 2909, 5459 ~ 6809, 5864 ~ 7350 구간별로 순회하며 totalSec 배열의 값을 1씩 증가시킨다.
👉🏻 totalSec 배열에서 큰 값을 가진다는 것은 누적 재생 시간이 많다는 의미가 된다.

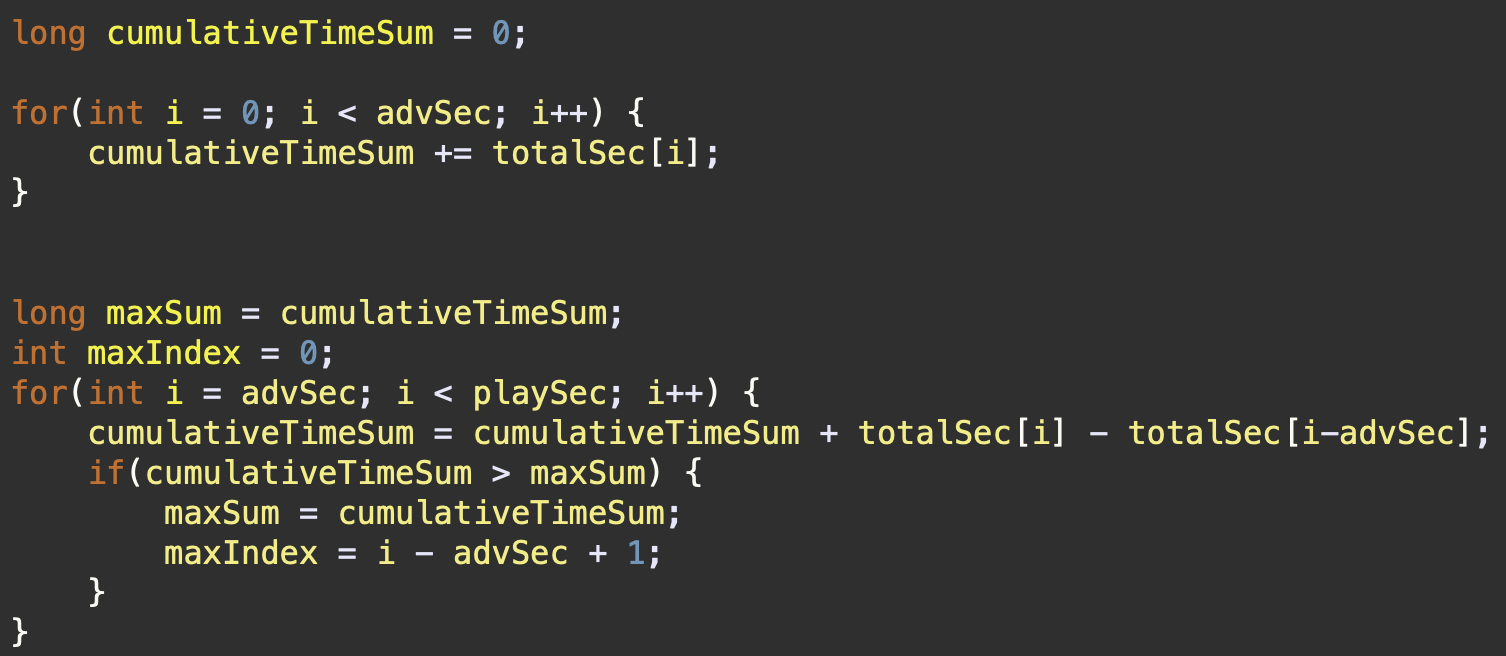
위 로직은 슬라이딩 윈도우 기법을 이용한 방법으로 전체 배열을 매번 처음부터 끝까지 다시 계산하지 않고도, 윈도우(광고 재생시간에 해당하는 구간)를 한 칸씩 옮기면서 누적 시청 시간을 효율적으로 업데이트할 수 있다.

초기 누적 시간을 계산하는 로직은 슬라이딩 원도우 알고리즘을 시작하기 전에 필요한 기준점을 설정한다. 이는 슬라이딩 윈도우의 첫 번째 위치에 해당하며, 이후 윈도우를 한 칸씩 옮겨가며 각 구간의 누적 시청 시간을 계산할 때 기준으로 사용된다.

초기 누적 시청 시간 설정 :

(cumulativeTimeSum) 변수는 공익광고의 전체 길이 (advSec)에 대해 동영상이 재생된 시간을 누적하는 데 사용된다.

첫 번째 for 루프( 0부터 advSec까지)는 초기 윈도우에 해당하는 모든 시청자의 시청 시간을 더하여 cumulativeTimeSum을 계산한다.

이 값은 최적의 광고 삽입 지점을 결정하기 위한 첫 번째 데이터 포인트로, 이후 윈도우를 이동하며 각 위치에서의 누적 시청 시간을 비교하는 기준점이 된다.

슬라이딩 윈도우를 이용한 누적 시청 시간 업데이트 :

윈도우를 한 칸씩 오른쪽으로 이동하면서, 새로운 구간의 시작점을 포함하고 이전 구간의 시작점을 제외함으로써 누적 시청 시간을 갱신한다. 이 때문에 광고 재생 시간(advSec) 이후부터 시작하는 두 번째 for루프가 필요하다.

이 과정에서 각 단계에서 윈도우의 오른쪽 끝에 있는 새 시청자 수(totalSec[i])를 추가하고, 윈도우의 왼쪽 끝에 있던 시청자 수(totalSec[i - advSec]를 빼줌으로써, 빠르게 누적 시청 시간을 업데이트할 수 있다.

이러한 방식으로 전체 배열을 한 번만 순회하면서 각 시점에서의 누적 시청 시간을 효율적으로 계산할 수 있다.

최대 누적 시청 시간과 인덱스 찾기 :

슬라이딩 윈도우가 전체 재생 시간(playSec)동안 이동할 때마다, 현재의 cumulativeTimeSum이 이전의 최대 누적 시청 시간(maxSum)보다 큰지 비교한다.

만약 현재의 누적 시청 시간이 더 크다면, 이는 새로운 최적의 광고 삽입 지점을 찾은 것이므로, maxSum과 maxIndex를 현재 값으로 업데이트한다.

👏🏻 슬라이딩 윈도우 기법의 시간 복잡도는 O(n)으로 최적의 광고 삽입 지점을 효과적이고 정확하게 찾을 수 있다. 전체 시청 시간이 n일 때, 각 시점에 대해 최대 한 번의 연산만 수행되므로, 이 알고리즘은 대량의 데이터에서도 빠르게 최적의 광고 삽입 지점을 찾을 수 있다.

`양과 늑대`

문3) 2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다. 이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다. 각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다. 이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며, 당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다. 당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서 최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.

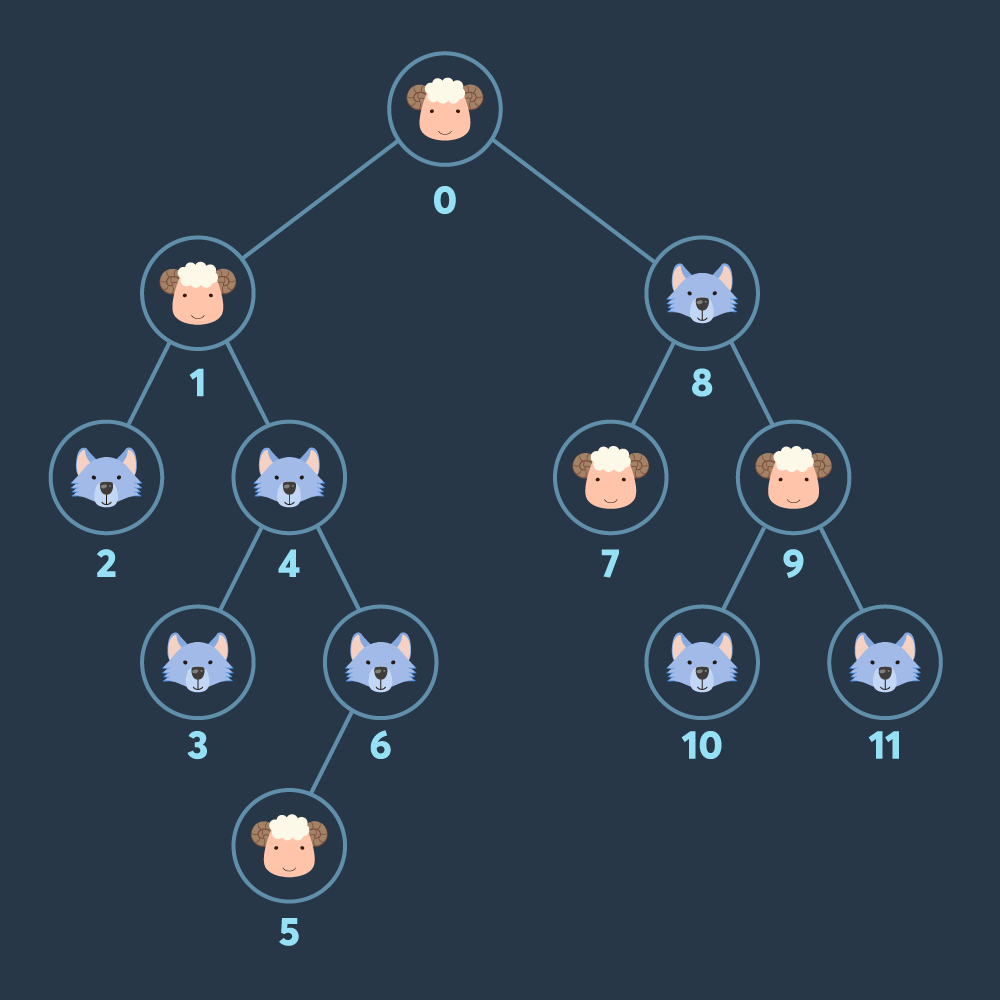
예를 들어, 위 그림의 경우(루트 노드에는 항상 양이 있습니다) 0번 노드(루트 노드)에서 출발하면 양을 한마리 모을 수 있습니다. 다음으로 1번 노드로 이동하면 당신이 모은 양은 두 마리가 됩니다. 이때, 바로 4번 노드로 이동하면 늑대 한 마리가 당신을 따라오게 됩니다. 아직은 양 2마리, 늑대 1마리로 양이 잡아먹히지 않지만, 이후에 갈 수 있는 아직 방문하지 않은 모든 노드(2, 3, 6, 8번)에는 늑대가 있습니다. 이어서 늑대가 있는 노드로 이동한다면(예를 들어 바로 6번 노드로 이동한다면) 양 2마리, 늑대 2마리가 되어 양이 모두 잡아먹힙니다. 여기서는 0번, 1번 노드를 방문하여 양을 2마리 모은 후, 8번 노드로 이동한 후(양 2마리 늑대 1마리) 이어서 7번, 9번 노드를 방문하면 양 4마리 늑대 1마리가 됩니다. 이제 4번, 6번 노드로 이동하면 양 4마리, 늑대 3마리가 되며, 이제 5번 노드로 이동할 수 있게 됩니다. 따라서 양을 최대 5마리 모을 수 있습니다.

각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info, 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges가 매개변수로 주어질 때, 문제에 제시된 조건에 따라 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리인지 return 하도록 solution 함수를 완성해주세요.

제한 사항

제한사항

2 ≤ info의 길이 ≤ 17
- info의 원소는 0 또는 1 입니다.
- info[i]는 i번 노드에 있는 양 또는 늑대를 나타냅니다.
- 0은 양, 1은 늑대를 의미합니다.
- info[0]의 값은 항상 0입니다. 즉, 0번 노드(루트 노드)에는 항상 양이 있습니다.
edges의 세로(행) 길이 = info의 길이 - 1
- edges의 가로(열) 길이 = 2
- edges의 각 행은 [부모 노드 번호, 자식 노드 번호] 형태로, 서로 연결된 두 노드를 나타냅니다.
- 동일한 간선에 대한 정보가 중복해서 주어지지 않습니다.
- 항상 하나의 이진 트리 형태로 입력이 주어지며, 잘못된 데이터가 주어지는 경우는 없습니다.
- 0번 노드는 항상 루트 노드입니다.

입출력 예

info	edges	result
`[0,0,1,1,1,0,1,0,1,0,1,1]`	`[[0,1],[1,2],[1,4],[0,8],[8,7],[9,10],[9,11],[4,3],[6,5],[4,6],[8,9]]`	5
`[0,1,0,1,1,0,1,0,0,1,0]`	`[[0,1],[0,2],[1,3],[1,4],[2,5],[2,6],[3,7],[4,8],[6,9],[9,10]]`	5

입출력 예 설명

입출력 예 #2

주어진 입력은 다음 그림과 같습니다.

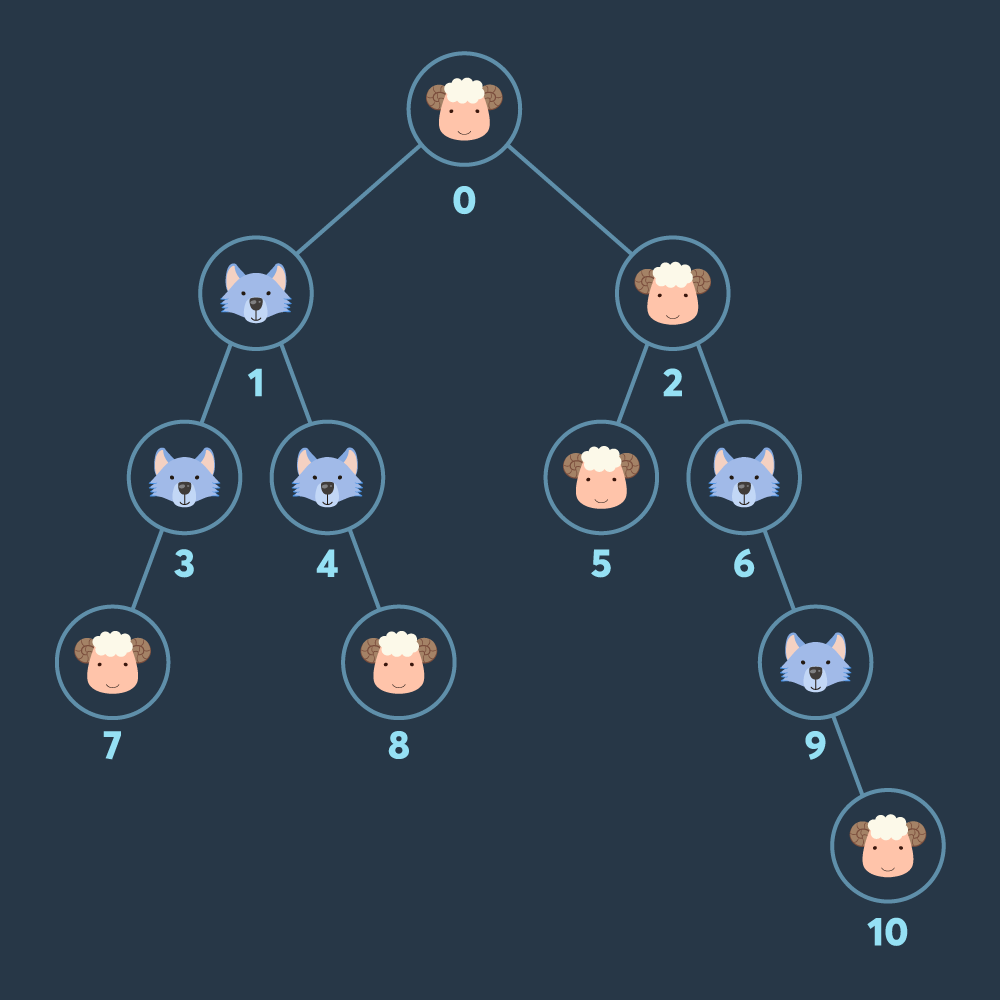
0번 - 2번 - 5번 - 1번 - 4번 - 8번 - 3번 - 7번 노드 순으로 이동하면 양 5마리 늑대 3마리가 됩니다. 여기서 6번, 9번 노드로 이동하면 양 5마리, 늑대 5마리가 되어 양이 모두 잡아먹히게 됩니다. 따라서 늑대에게 잡아먹히지 않도록 하면서 최대로 모을 수 있는 양은 5마리입니다.

나의 풀이

visited 3차원 배열을 사용한 dfs 풀이

package programmers;

import java.util.ArrayList;

public class SheepAndWolf {
	
	
	static int[] Node;
	static ArrayList<Integer>[]  graph = new ArrayList[17];
	static boolean[][][] visited;
	static int maxSheep;
	
	static void dfs(int pos, int sheep, int wolves) {
		if(visited[pos][sheep][wolves]) return;
		visited[pos][sheep][wolves] = true;
		
		int backupSheep = sheep;
		int backupWolves = wolves;
		
		int backupNode = Node[pos];
		
		
		if(Node[pos] == 0) sheep++;
		else if(Node[pos] == 1) wolves++;
		
		Node[pos] = -1;
		
		if(wolves < sheep) {
			maxSheep = Math.max(maxSheep, sheep);
			for(int next : graph[pos]) {
				dfs(next, sheep, wolves);
			}
		}
		
		Node[pos] = backupNode;
		visited[pos][backupSheep][backupWolves] = false;
		
	}
	
	public static int solution(int[] info, int[][] edges) {
        
		Node = info; 
		
        for(int i = 0; i < Node.length; i++) {
        	graph[i] = new ArrayList<>();
        }
        
        for(int[] edge : edges) {
        	graph[edge[0]].add(edge[1]);
        	graph[edge[1]].add(edge[0]);
        }
        
        visited = new boolean[17][18][18];
        maxSheep = 0;
        dfs(0, 0, 0);
       
        
        
       
        System.out.println(maxSheep);
        return maxSheep;
    }
	
	public static void main(String[] args) {
		int[] info = {0,0,1,1,1,0,1,0,1,0,1,1};
		int[][] edges = {{0,1},{1,2},{1,4},{0,8},{8,7},{9,10},{9,11},{4,3},{6,5},{4,6},{8,9}};
		solution(info, edges);
	}

}

리스트 타입의 배열 및 Set을 활용한 풀이

package programmers;

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;

public class SheepAndWolf {
    
	static List<Integer>[] graph;
	static int answer = 0;
	
	public static void dfs(int index, int sheep, int wolves, int[] info, Set<Integer> unused ) {
		
		if(sheep == wolves) return;
		
		answer = Math.max(answer, sheep);
		
		for(int next : graph[index]) {
			unused.add(next);
		}
		
		
		for(int next : unused) {
			
			Set<Integer> set = new HashSet<>(unused);
			set.remove(next);
			if(info[next] == 1) {
				dfs(next, sheep, wolves+1, info, set);
			}else {
				dfs(next, sheep+1, wolves, info, set);
			}
		}
	}

    
    public static int solution(int[] info, int[][] edges) {
       
    	int n = info.length;
    	graph = new List[n];
    	
    	for(int i = 0; i < n; i++) graph[i] = new ArrayList<>();
    	
    	for(int[] edge : edges) {
    		graph[edge[0]].add(edge[1]);
    	}

    	
    	
    	dfs(0, 1, 0, info, new HashSet<>());
    	
    	
        return answer;
    }
	
	public static void main(String[] args) {
		int[] info = {0,0,1,1,1,0,1,0,1,0,1,1};
		int[][] edges = {{0,1},{1,2},{1,4},{0,8},{8,7},{9,10},{9,11},{4,3},{6,5},{4,6},{8,9}};
		solution(info, edges);
	}

}

나의 생각

재방문 가능성 : 이 문제에서는 노드의 재방문이 가능해야 한다. 이는 양을 더 모으기 위해 이전에 방문한 노드로 다시 돌아갈 수 있어야함을 의미한다.

상태 추적 : 각 노드 방문 시 양과 늑대의 수를 추적해야한다. 늑대의 수가 양의 수보다 많아지는 순간 탐색을 중단하고 다른 경로를 탐색해야한다.

visited 3차원 배열을 사용한 dfs 풀이	리스트 타입의 배열 및 Set을 활용한 풀이

특징	첫 번째 풀이	두 번째 풀이
탐색 방법	깊이 우선 탐색(DFS)	깊이 우선 탐색(DFS) + 동적 계획법(DP)적 요소
상태 관리	3차원 배열을 이용한 방문 상태 관리	HashSet을 이용한 유연한 상태 관리
노드 처리	노드의 상태를 변경하며 탐색 후 복구	노드의 상태를 변경하지 않고 탐색
이점	상태 복구를 통한 명확한 백트래킹	유연한 경로 변경과 다양한 경우의 수 탐색
효율성	높은 메모리 사용량, 중복 상태 방문 최소화	더 낮은 메모리 사용량, 탐색 공간의 유연한 확장
적합한 문제 유형	상태 변화가 중요한 문제 해결에 적합	다양한 경로와 상태를 고려해야 하는 문제에 적합

위 문제에서 내가 특히 고민했던 두 가지 사항은 다음과 같다.

간선 정보의 저장 방식 선택 :
👉🏻 배열과 리스트 두 가지 방법이 생각났는데, 리스트 구조를 사용함으로써 노드 간의 동적인 연결 관계를 나타내었음

상태 관리를 위한 자료구조 선택 :
👉🏻 보통 1차원 visited 배열로 선언하였는데, 위 문제의 경우 재방문을 할 수 있기때문에 조금 더 복잡한 상태 관리가 필요했음

👏🏻 위 문제의 경우 Set 자료 구조를 선택한 이점은 다음과 같다.

중복 제거 : Set은 중복된 요소를 저장하지 않음. 이 문제에서는 같은 노드를 여러 번 방문할 수 있지만, 특정 상태(현재 노드, 양의 수, 늑대의 수)에서 방문 가능한 노드들의 집합을 관리할 때 중복된 노드를 추가로 고려할 필요가 없다. 따라서, Set을 사용하면 자동으로 중복을 제거하여 효율적으로 상태를 관리할 수 있다.

탐색 효율성 : Set은 요소의 존재 여부를 빠르게 확인할 수 있다. 이는 다음 탐색 단계를 결정할 때 이미 방문했거나 방문할 예정인 노드를 효율적으로 필터링할 수 있게 해준다. 특히, HashSet을 사용할 경우, 평균적으로 상수 시간에 요소의 존재 여부를 확인할 수 있어 탐색 과정이 빨라진다.

동적 상태 관리 : 문제 해결 과정에서 다음에 방문할 노드들의 집합은 동적으로 변화한다. Set을 사용하면 이러한 동적 상태를 쉽게 관리할 수 있다. 새로운 노드를 방문할 때마다 Set에 추가하고, 더 이상 방문하지 않을 노드를 Set에서 제거함으로써 현재 상태를 유연하게 업데이트 할 수 있다.

재귀 호출 용이성 : 이 문제의 해결 방법에서는 재귀 호출을 사용하여 깊이 우선 탐색(DFS)을 수행한다. Set을 사용하면 현재 상태(방문하지 않은 노드들의 집합)를 새로운 재귀 호출에 쉽게 전달할 수 있다. 각 재귀 단계에서 Set의 복사본을 만들어 수정함으로써, 다른 탐색 경로에서의 상태 변화가 서로에게 영향을 주지 않도록 할 수 있다.

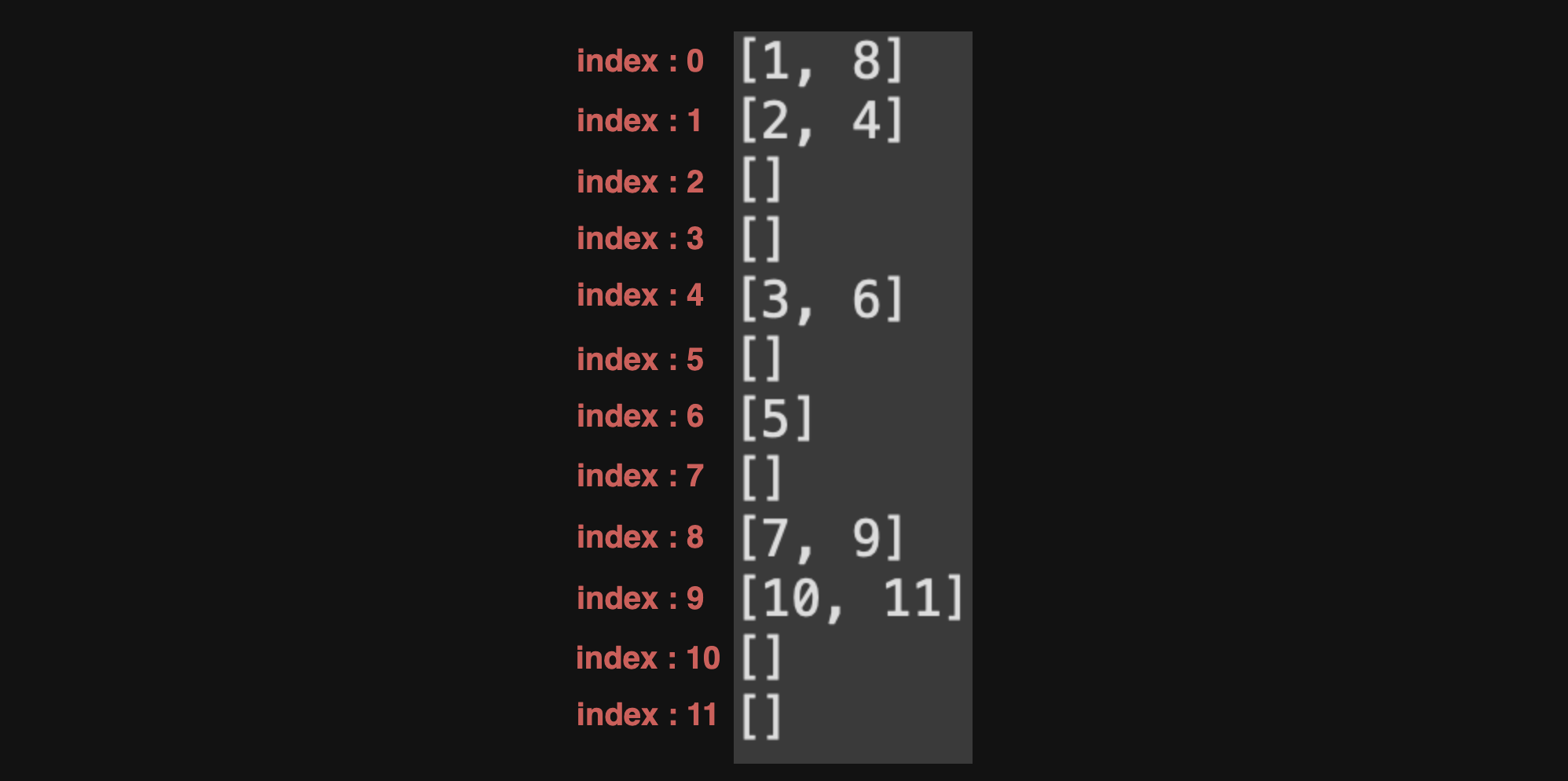
위 정보에서 알 수 있는 정보는
index 0 → 1, 8과 연결
index 1 → 2, 4와 연결
index 2 → ❌
index 3 → ❌
index 4 → 3, 6과 연결
index 5 → ❌
index 6 → 5와 연결
index 7 → ❌
index 8 → 7, 9와 연결
index 9 → 10, 11과 연결
index 10 → ❌
index 11 → ❌

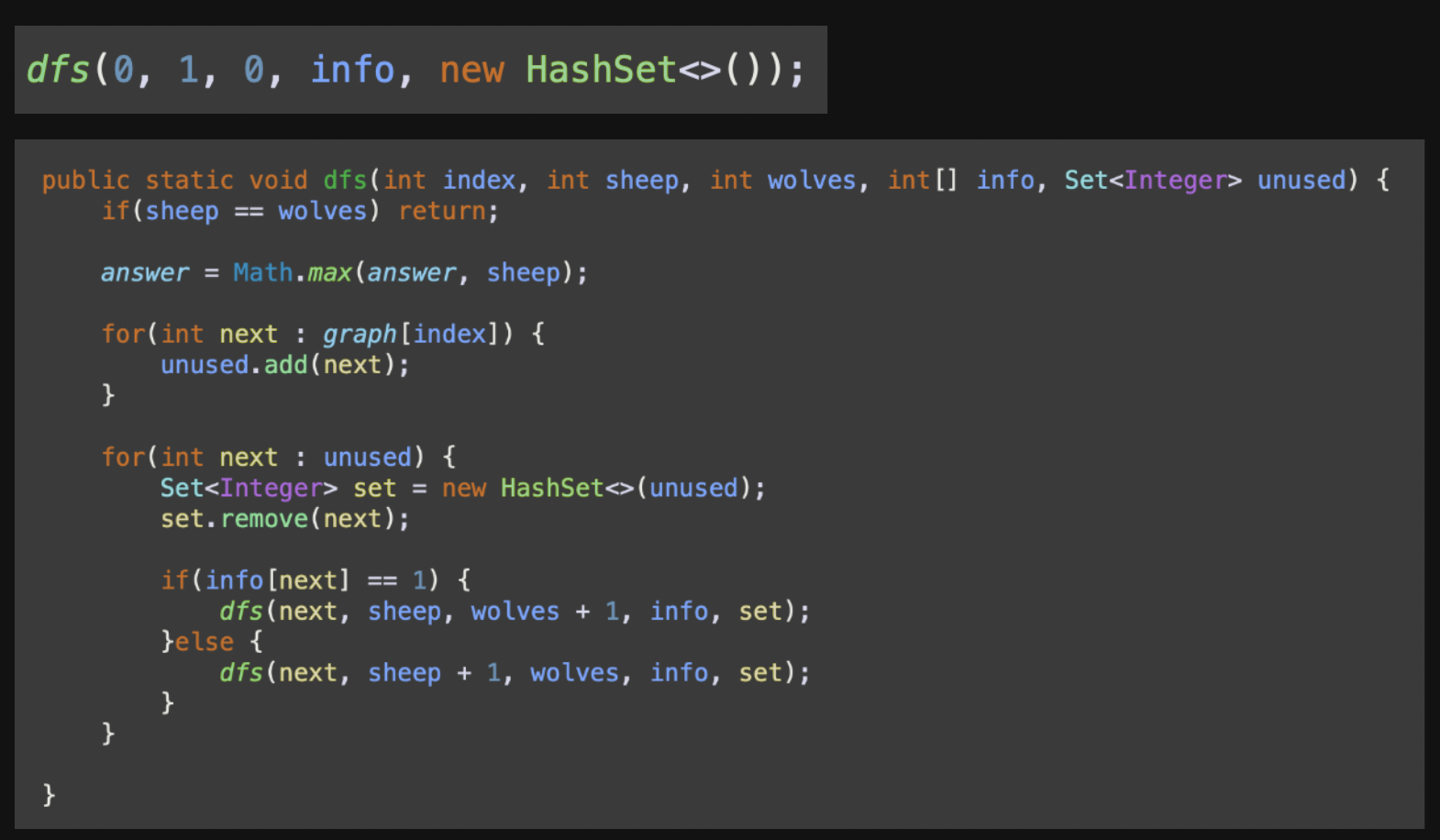
index 0을 예로 들면,
Root Node(0)은 1,8과 연결되어 있다.
따라서, unused set 자료 구조에
[1,8]이 저장된다.

다음, unused를 순회하면,
int next = 1부터 시작,
unused의 복사본 set에서 1을 제거

info[1] = 0 즉, 1번 node는 양이란 의미이므로, else문을 실행

dfs(1, 2 , 0 , info, set(8)) 호출
graph(1)

unsued set 자료구조에 [2,4] 저장

복사본 set 자료구조에서 int next = 2 제거
info[2] = 1 즉, 2번 node는 늑대이므로, if문 실행

dfs(2, 2, 1, info, set(4,8) 호출
・
・
・
👉🏻 graph 순회를 모두 마친 후의 answer 최대값을 answer 전역변수에 저장하여 이를 리턴

보행자 천국

문4) 카카오내비 개발자인 제이지는 시내 중심가의 경로 탐색 알고리즘 개발 업무를 담당하고 있다. 최근 들어 보행자가 자유롭고 편리하게 걸을 수 있도록 보행자 중심의 교통 체계가 도입되면서 도심의 일부 구역은 자동차 통행이 금지되고, 일부 교차로에서는 보행자 안전을 위해 좌회전이나 우회전이 금지되기도 했다. 복잡해진 도로 환경으로 인해 기존의 경로 탐색 알고리즘을 보완해야 할 필요가 생겼다.

도시 중심가의 지도는 m × n 크기의 격자 모양 배열 city_map으로 주어진다. 자동차는 오른쪽 또는 아래 방향으로 한 칸씩 이동 가능하다.

city_map[i][j]에는 도로의 상황을 나타내는 값이 저장되어 있다.

0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)

도시의 도로 상태가 입력으로 주어졌을 때, 왼쪽 위의 출발점에서 오른쪽 아래 도착점까지 자동차로 이동 가능한 전체 가능한 경로 수를 출력하는 프로그램을 작성하라. 이때 가능한 경로의 수는 컴퓨터가 표현할 수 있는 정수의 범위를 넘어설 수 있으므로, 가능한 경로 수를 20170805로 나눈 나머지 값을 출력하라.

입력 형식

입력은 도시의 크기를 나타내는 m과 n, 그리고 지도를 나타내는 2차원 배열 city_map으로 주어진다. 제한조건은 아래와 같다.

1 <= m, n <= 500
city_map의 크기는 m × n이다.
배열의 모든 원소의 값은 0, 1, 2 중 하나이다.
출발점의 좌표는 (0, 0), 도착점의 좌표는 (m - 1, n - 1)이다.
출발점과 도착점의 city_map[i][j] 값은 0이다.

출력 형식

출발점에서 도착점까지 이동 가능한 전체 경로의 수를 20170805로 나눈 나머지를 리턴한다.

예제 입출력

m	n	city_map	answer
3	3	`[[0, 0, 0], [0, 0, 0], [0, 0, 0]]`	6
3	6	`[[0, 2, 0, 0, 0, 2], [0, 0, 2, 0, 1, 0], [1, 0, 0, 2, 2, 0]]`	2

입출력 예 설명

첫 번째 예제는 모든 도로가 제한 없이 통행 가능한 경우로, 가능한 경우의 수는 6가지이다.
두 번째 예제는 문제 설명에 있는 그림의 경우이다. 가능한 경우의 수는 빨간 실선과 노란 점선 2가지뿐이다.

나의 풀이

package programmers;

import java.util.Arrays;

public class PedestrianParadise {
	static int MOD = 20170805;
   
	public static int solution(int m, int n, int[][] cityMap) {
		
		int[][] right = new int[m + 1][n + 1];
        int[][] down = new int[m + 1][n + 1];
        
        right[0][0] = 1;
        

        
        for (int y = 0; y < m; y++) {
            for (int x = 0; x < n; x++) {
                if (cityMap[y][x] == 0) {
                    down[y+1][x] += (right[y][x] + down[y][x]) % MOD;
                    right[y][x+1] += (right[y][x] + down[y][x]) % MOD;
                } else if (cityMap[y][x] == 2) {
                    down[y+1][x] = down[y][x] % MOD;
                    right[y][x+1] = right[y][x] % MOD;
                }
                
            }
        }
        
        
        return (right[m-1][n-1] + down[m-1][n-1]) % MOD ;
    }
	
	public static void main(String[] args) {
		int[][] cityMap = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
		solution(3, 3, cityMap);
	}

}

두번째 방법

package programmers;

public class PedestrianParadise {
	static int MOD = 20170805;
   
	public static int solution(int m, int n, int[][] cityMap) {
		
		int[][] right = new int[m + 1][n + 1];
        int[][] down = new int[m + 1][n + 1];
        
        right[1][1] = 1;
        down[1][1] = 1;
        
        for(int y = 1; y <= m; y++) {
        	for(int x = 1; x <= n; x++) {
        		if(cityMap[y-1][x-1] == 0) {
        			right[y][x] += (right[y][x-1] + down[y-1][x]) % MOD;
        			down[y][x] += (right[y][x-1] + down[y-1][x]) % MOD;
        		}else if(cityMap[y-1][x-1] == 2) {
        			right[y][x] = right[y][x-1];
        			down[y][x] = down[y-1][x];
        		}
        	}
        }
      
       
        
        System.out.println((right[m][n - 1] + down[m - 1][n]) % MOD);
        return (right[m][n - 1] + down[m - 1][n]) % MOD;
    }
	
	public static void main(String[] args) {
		int[][] cityMap = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
		solution(3, 3, cityMap);
	}

}

나의 생각

문제를 보자마자 본능적으로 DP로 문제를 접근해야겠다고 생각들었다. 그 이유는 출발 지점에서 목적지 까지 가는 길이 중복될 수 있기 때문이다.

문제에서 주어진 조건을 먼저 살펴보자.

자동차는 오른쪽 또는 아래 방향으로 한 칸씩 이동 가능하다.
👉🏻 즉 상,하,좌,우 모든 방향을 확인할 필요는 없다.
0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
👉🏻 이 경우도, 오른쪽 방향과 아래 방향만 확인하면 된다.
1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
👉🏻 1인 경우 무시(갈 수 있는 길이 없기때문에 아무런 동작을 하지 않는다)
2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)
👉🏻 말그대로 이전 위치의 값을 그대로 사용한다는 의미가 된다.

위 조건을 바탕으로 경우의 수를 생각해보자

cityMap[y][x] == 0 인 경우

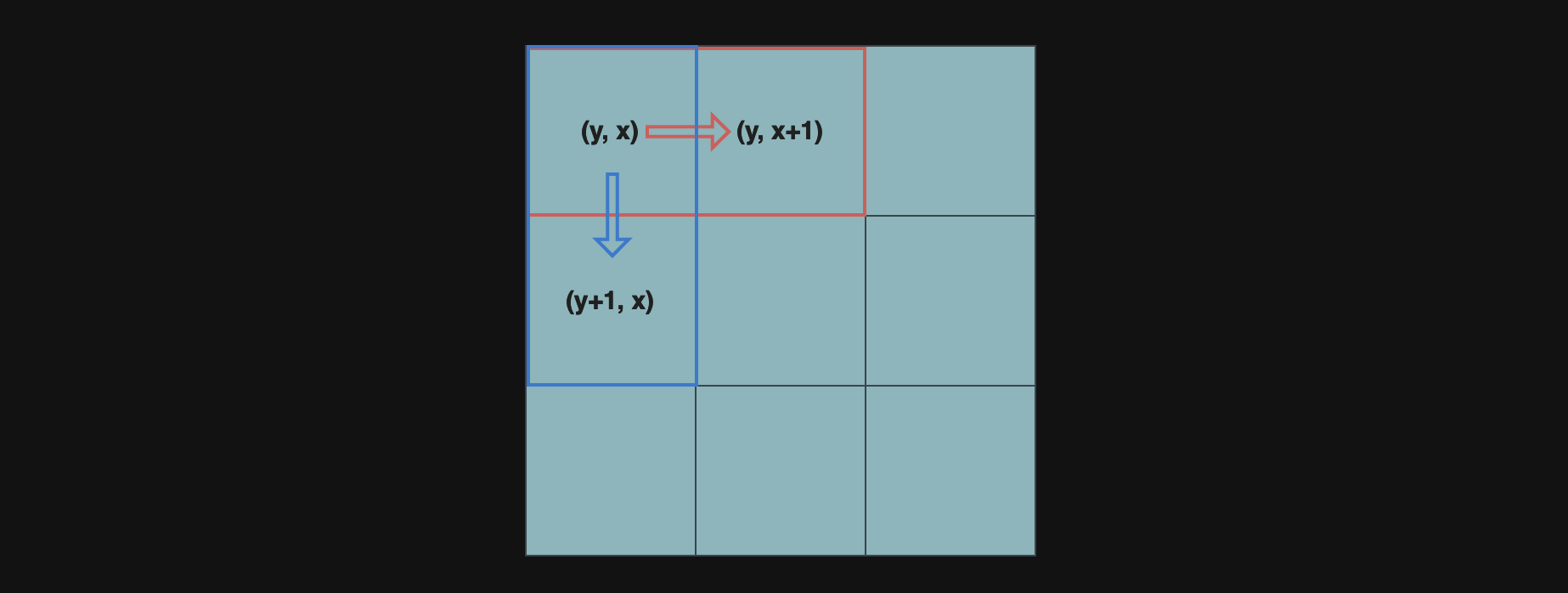
그림에 나타난 상황처럼, cityMap[y][x] == 0 인 경우 (y,x) 위치에서는 오른쪽((y, x+1))과 아래쪽 (y+1, x)으로의 이동이 가능하다.
이때, (y+1,x)로 내려가는 경로의 수(down[y+1][x])는 현재 위치 (y,x)로 오는 두 가지 경우, 즉 위에서 내려오는 경로(down[y][x])와 왼쪽에서 오른쪽으로 오는 경로(right[y][x])의 합과 같다.
왜냐하면, (y,x)위치에서 오른쪽 또는 위에서 온 모든 사람들은 아래로 내려갈 수 있기 때문이다.
마찬가지로, (y, x+1)로 오른쪽으로 이동하는 경로의 수(right[y][x+1])는 현재 위치 (y, x)로 오는 위에서 내려오는 경로(down[y][x])와 왼쪽에서 오른쪽으로 오는 경로(right[y][x])의 합과 같다. (y, x) 위치에서 오른쪽으로 이동할 수 있는 모든 사람들은 왼쪽 또는 위에서 온 사람들이기 때문이다.

이를 점화식으로 나타내면 다음과 같다.

down[y+1][x] += (right[y][x] + down[y][x]) % MOD;

right[y][x+1] += (right[y][x] + down[y][x]) % MOD;

cityMap[y][x] == 1 인 경우

👉🏻 어느 쪽으로도 이동할 수 없으므로 무시한다.

cityMap[y][x] == 2 인 경우

왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다.
- 이는 각 위치에서 차량이 이전에 이동해 온 방향을 계속해서 유지해야함을 의미한다.

이를 그림으로 나타내면 다음과 같다.

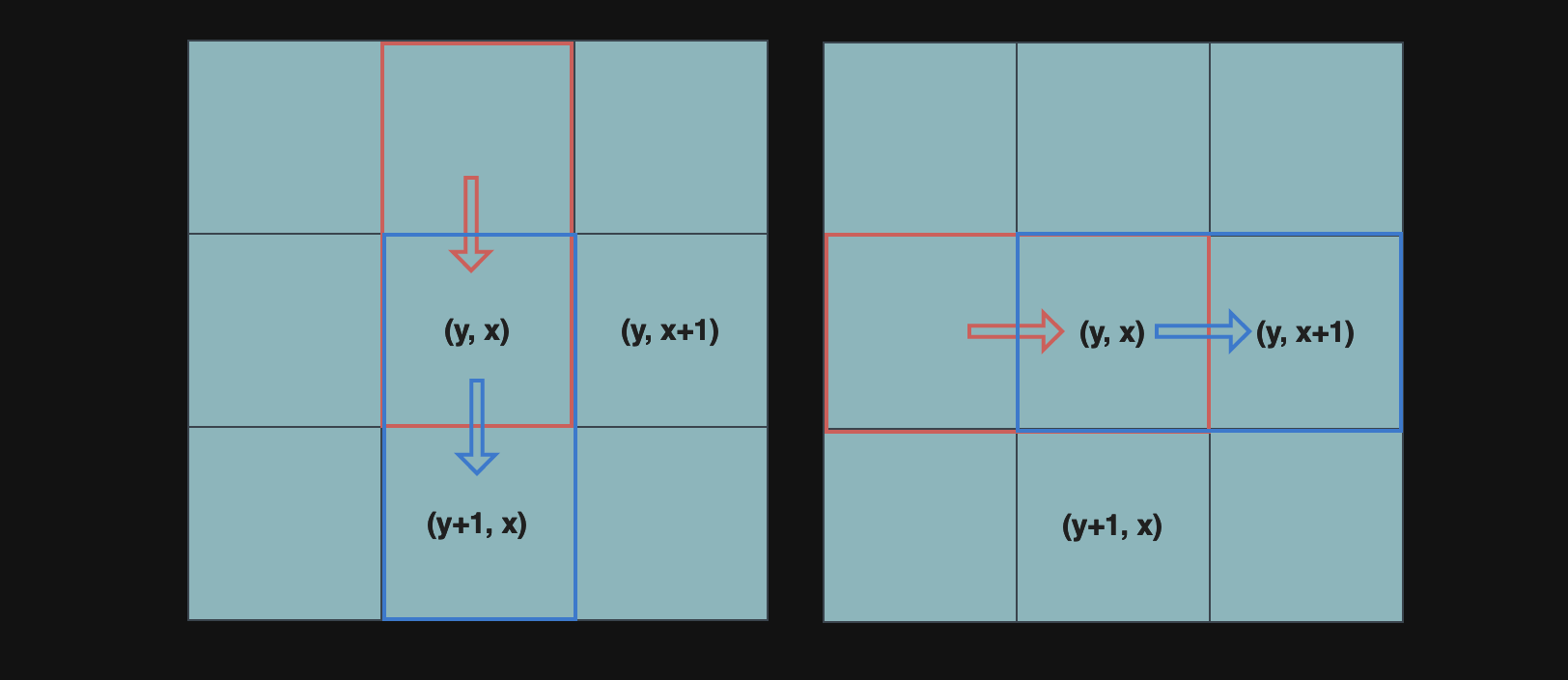
down 배열은 오직 위에서 아래로 내려오는 경로만 계산한다. 이는 해당 위치에 위쪽에서 내려온 차량만이 계속해서 아래쪽으로 진행할 수 있음을 의미하므로, down[y+1][x]의 값은 이전 down[y][x] 값에만 의존한다.
right 배열은 오직 왼쪽에서 오른쪽으로 이동하는 경로만 계산한다. 이는 해당 위치에 왼쪽에서 온 차량만이 계속해서 오른쪽으로 진행할 수 있음을 의미하므로, right[y][x+1]의 값은 이전 right[y][x]값에만 의존한다.

이를 점화식으로 나타내면 다음과 같다.

down[y+1][x] = down[y][x] % MOD;

right[y][x+1] = right[y][x] % MOD;

배열의 초기값을 right, down 둘 중 하나만 1로 초기화한 이유는 무엇인가?

right[0][0] = 1 or down[0][0] = 1로 설정하는 것은 시작점에서 이동 경로를 시작할 수 있는 방향을 나타낸다. 그러나 둘 다 1로 설정하면, 시작점에서 오른쪽 또는 아래로의 이동이 두 번 카운트되어, 실제 가능한 경로 수보다 더 많은 경로 수가 계산되는 문제가 발생한다.
문제의 초기 조건에서 시작점에서 오른쪽으로 이동하거나 아래로 이동하는 경우는 각각 하나의 유효한 경로만 존재한다. 따라서, 시작점에서 오른쪽으로 이동할 수 있는 경로를 right 배열을 통해 1로 설정하고, down 배열은 0으로 남겨두어야 한다. 이렇게 하면 시작점에서 오른쪽으로 이동하는 경로는 한 번만 계산되고, 시작점에서 바로 아래로 이동하는 경로는 계산되지 않는다.

미로 탈출 명령어

문5) n x m 격자 미로가 주어집니다. 당신은 미로의 (x, y)에서 출발해 (r, c)로 이동해서 탈출해야 합니다.

단, 미로를 탈출하는 조건이 세 가지 있습니다.

격자의 바깥으로는 나갈 수 없습니다.
(x, y)에서 (r, c)까지 이동하는 거리가 총 k여야 합니다. 이때, (x, y)와 (r, c)격자를 포함해, 같은 격자를 두 번 이상 방문해도 됩니다.
미로에서 탈출한 경로를 문자열로 나타냈을 때, 문자열이 사전 순으로 가장 빠른 경로로 탈출해야 합니다.

이동 경로는 다음과 같이 문자열로 바꿀 수 있습니다.

l: 왼쪽으로 한 칸 이동
r: 오른쪽으로 한 칸 이동
u: 위쪽으로 한 칸 이동
d: 아래쪽으로 한 칸 이동

예를 들어, 왼쪽으로 한 칸, 위로 한 칸, 왼쪽으로 한 칸 움직였다면, 문자열 "lul"로 나타낼 수 있습니다.

미로에서는 인접한 상, 하, 좌, 우 격자로 한 칸씩 이동할 수 있습니다.

예를 들어 다음과 같이 3 x 4 격자가 있다고 가정해 보겠습니다.

....
..S.
E...

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (3, 4)입니다. .은 빈 공간, S는 출발 지점, E는 탈출 지점입니다.

탈출까지 이동해야 하는 거리 k가 5라면 다음과 같은 경로로 탈출할 수 있습니다.

lldud
ulldd
rdlll
dllrl
dllud
...

이때 dllrl보다 사전 순으로 빠른 경로로 탈출할 수는 없습니다.

격자의 크기를 뜻하는 정수 n, m, 출발 위치를 뜻하는 정수 x, y, 탈출 지점을 뜻하는 정수 r, c, 탈출까지 이동해야 하는 거리를 뜻하는 정수 k가 매개변수로 주어집니다. 이때, 미로를 탈출하기 위한 경로를 return 하도록 solution 함수를 완성해주세요. 단, 위 조건대로 미로를 탈출할 수 없는 경우 "impossible"을 return 해야 합니다.

제한사항

2 ≤ n (= 미로의 세로 길이) ≤ 50
2 ≤ m (= 미로의 가로 길이) ≤ 50
1 ≤ x ≤ n
1 ≤ y ≤ m
1 ≤ r ≤ n
1 ≤ c ≤ m
(x, y) ≠ (r, c)
1 ≤ k ≤ 2,500

입출력 예

n	m	x	y	r	c	k	result
3	4	2	3	3	1	5	`dllrl`
2	2	1	1	2	2	2	`dr`
3	3	1	2	3	3	4	`impossible`

입출력 예 설명

입출력 예 #2

미로의 크기는 2 x 2입니다. 출발 지점은 (1, 1)이고, 탈출 지점은 (2, 2)입니다.
빈 공간은 ., 출발 지점을 S, 탈출 지점을 E로 나타내면 다음과 같습니다.

S.
.E

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (2, 2)입니다.

탈출까지 이동해야 하는 거리 k가 2이므로 다음과 같은 경로로 탈출할 수 있습니다.

"dr"이 사전 순으로 가장 빠른 경로입니다. 따라서 "dr"을 return 해야 합니다.

입출력 예 #3

미로의 크기는 3 x 3입니다. 출발 지점은 (1, 2)이고, 탈출 지점은 (3, 3)입니다.

빈 공간은 ., 출발 지점을 S, 탈출 지점을 E로 나타내면 다음과 같습니다.

.S.
...
..E

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (3, 3)입니다.

탈출까지 이동해야 하는 거리 k가 4입니다. 이때, 이동 거리가 4이면서, S에서 E까지 이동할 수 있는 경로는 존재하지 않습니다.

따라서 "impossible"을 return 해야 합니다.

나의 풀이

dfs풀이 (시간초과로 실패)

package programmers;

public class MazeEscapeCommand {
	
	static int[][] DIRS = {{1,0},{0,-1},{0,1},{-1,0}}; 
	static char[] dirChars = {'d', 'l', 'r', 'u'}; 
	static String bestPath = null; 	
	
	
	public static void dfs(int x, int y, int r, int c, int k, StringBuilder path, int n, int m) {
		
		int remainingDistance = Math.abs(r - x) + Math.abs(c - y);
		
		if (k < remainingDistance) return;
        
        if ((k - remainingDistance) % 2 != 0) return;
		
        if (x == r && y == c && k == 0) {
            bestPath = path.toString();
            return;
        }
          
		for (int i = 0; i < 4; i++) { 
            int nx = x + DIRS[i][0];
            int ny = y + DIRS[i][1];
            if (nx > 0 && nx <= n && ny > 0 && ny <= m) { 
                path.append(dirChars[i]); 
                dfs(nx, ny, r, c, k - 1, path, n, m); 
                path.deleteCharAt(path.length() - 1); 
            }
        }
		
	}
	
	public static String solution(int n, int m, int x, int y, int r, int c, int k) {
		
		int length = Math.abs(x - r) + Math.abs(y - c);
        if (k < length || (k - length) % 2 != 0) {
            return "impossible";
        }
		
		StringBuilder path = new StringBuilder();
		dfs(x, y, r, c, k, path, n, m);
        
        return bestPath != null ? bestPath : "impossible";
    }
	public static void main(String[] args) {
		solution(3, 3, 1, 2, 3, 3, 4);
	}

}

dfs 최적화 로직(정답)

package programmers;

public class MazeEscapeCommand {
	
	static int[][] DIRS = {{1,0}, {0,-1}, {0,1}, {-1,0}};
    static char[] dirChars = {'d', 'l', 'r', 'u'};
    static String bestPath = null;

    public static boolean dfs(int x, int y, int r, int c, int k, StringBuilder path, int n, int m) {
        int remainingDistance = Math.abs(r - x) + Math.abs(c - y);

        if (k < remainingDistance || (k - remainingDistance) % 2 != 0) return false;

        if (x == r && y == c && k == 0) {
            bestPath = path.toString();
            return true; 
        }

        for (int i = 0; i < 4; i++) {
            int nx = x + DIRS[i][0];
            int ny = y + DIRS[i][1];
            if (nx > 0 && nx <= n && ny > 0 && ny <= m) {
                path.append(dirChars[i]);
                if (dfs(nx, ny, r, c, k - 1, path, n, m)) {
                    return true; 
                }
                path.deleteCharAt(path.length() - 1);
            }
        }
        return false; 
    }

    public static String solution(int n, int m, int x, int y, int r, int c, int k) {
        StringBuilder path = new StringBuilder();
        if (!dfs(x, y, r, c, k, path, n, m)) {
            return "impossible";
        }
        return bestPath;
    }
	public static void main(String[] args) {
		solution(3, 3, 1, 2, 3, 3, 4);
	}

}

조건 기반 경로 생성 로직

class Solution {
    public String solution(int n, int m, int x, int y, int r, int c, int k) {
        int distance = Math.abs(r - x) + Math.abs(c - y);
        if (distance > k) {
            return "impossible";
        }

        if ((k - distance) % 2 != 0) {
            return "impossible";
        }

        int down = Math.max(r - x, 0);
        int left = Math.max(y - c, 0);
        int right = Math.max(c - y, 0);
        int up = Math.max(x - r, 0);
        int pair = (k - distance) / 2;

        StringBuilder answer = new StringBuilder();

        for (int i = 0; i < k; i++) {
            if ((down > 0 || pair > 0) && x < n) {
                answer.append('d');
                if (down > 0) {
                    down--;
                } else {
                    pair--;
                    up++;
                }
                x++;
            } else if ((left > 0 || pair > 0) && y > 1) {
                answer.append('l');
                if (left > 0) {
                    left--;
                } else {
                    pair--;
                    right++;
                }
                y--;
            } else if ((right > 0 || pair > 0) && y < m) {
                answer.append('r');
                if (right > 0) {
                    right--;
                } else {
                    pair--;
                    left++;
                }
                y++;
            } else { 
                answer.append('u');
                if (up > 0) {
                    up--;
                } else {
                    pair--;
                    down++;
                }
                x--;
            }
        }
        return answer.toString();
    }
}

나의 생각

특성	원래 로직	최적화된 로직
DFS 반환 타입	`void`	`boolean`
탐색 중단 조건	최적 경로를 찾은 후에도 탐색 계속	최적 경로를 찾으면 즉시 탐색 중단
경로 찾기 성공 여부	`bestPath`가 `null`이 아닌지로 판단	직접적으로 `true` 또는 `false` 반환하여 성공 여부 판단
목적지 도달 조건	목적지에 도달하고 `k`가 0인 경우 `bestPath` 업데이트 후 탐색 중단 없음	목적지에 도달하고 `k`가 0인 경우 `bestPath` 업데이트 및 `true` 반환하여 탐색 중단
탐색 실패 시 반환값	`bestPath`가 `null`이면 "impossible" 반환	`dfs` 함수에서 `false` 반환 시 "impossible" 반환
반환 방식의 차이	`bestPath` 초기화 후 모든 탐색 시도	최적 경로 찾는 즉시 탐색 중단 및 `bestPath` 반환

처음 내가 생각했던 방법은 dfs를 사용한 방법이였는데, 탈출 조건을 찾아서 설정하면 불필요한 탐색을 줄일수 있겠다고 생각하였다.

분명 정답을 도출하긴하나, 시간초과로 실패를 반복하였다.

`DFS와 가지치기(Pruning)`

1. 첫 번째 로직의 한계

첫 번째 로직은 깊이 우선 탐색(DFS)을 이용하여 미로 탈출 경로를 찾는 알고리즘을 구현하였는데, 유효한 경로를 찾은 후에도 계속해서 탐색을 수행하는 비효율성 문제를 갖고 있었다. 특히, 목적지에 도달하고 필요한 이동 횟수를 모두 사용했음에도 불구하고, 모든 가능한 경로에 대한 추가 탐색을 계속하였다.

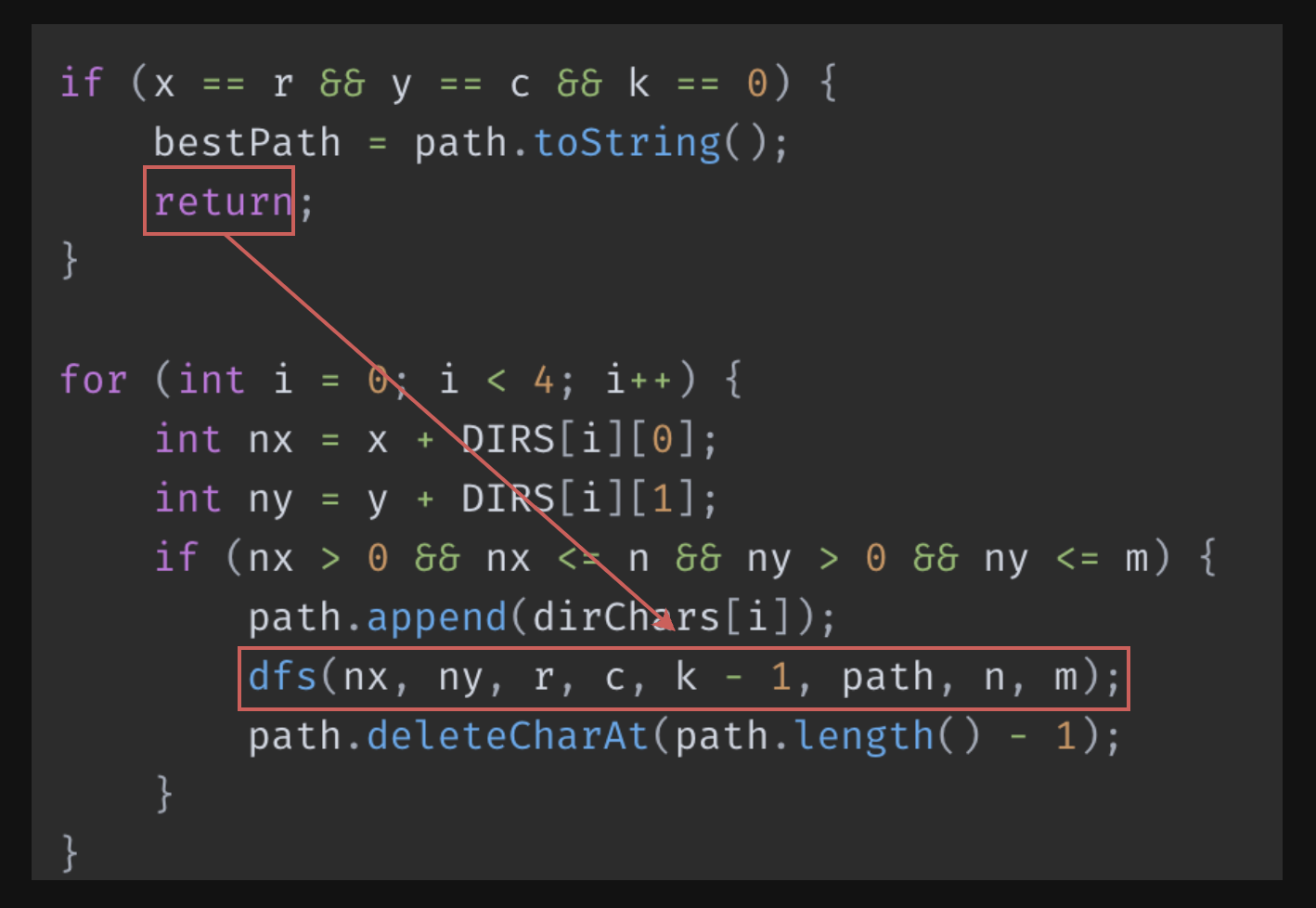
위 조건문에서 경로를 찾았을 때 return을 통해 탐색을 종료한다. 그러나 이는 현재 경로에서만 탐색을 종료하며, 다른 잠재적 경로에 대한 탐색을 중단하지 않는다는것을 발견하였다.

2. 두 번째 로직으로의 개선

두 번째 로직은 첫 번째 로직의 비효율성을 해결하기 위해 몇 가지 중요한 개선을 하였다. 핵심 개선 사항으로 유효한 경로를 찾으면 즉시 탐색을 중단하고 true를 반환하여, 추가적인 탐색을 방지하는 것이였다.

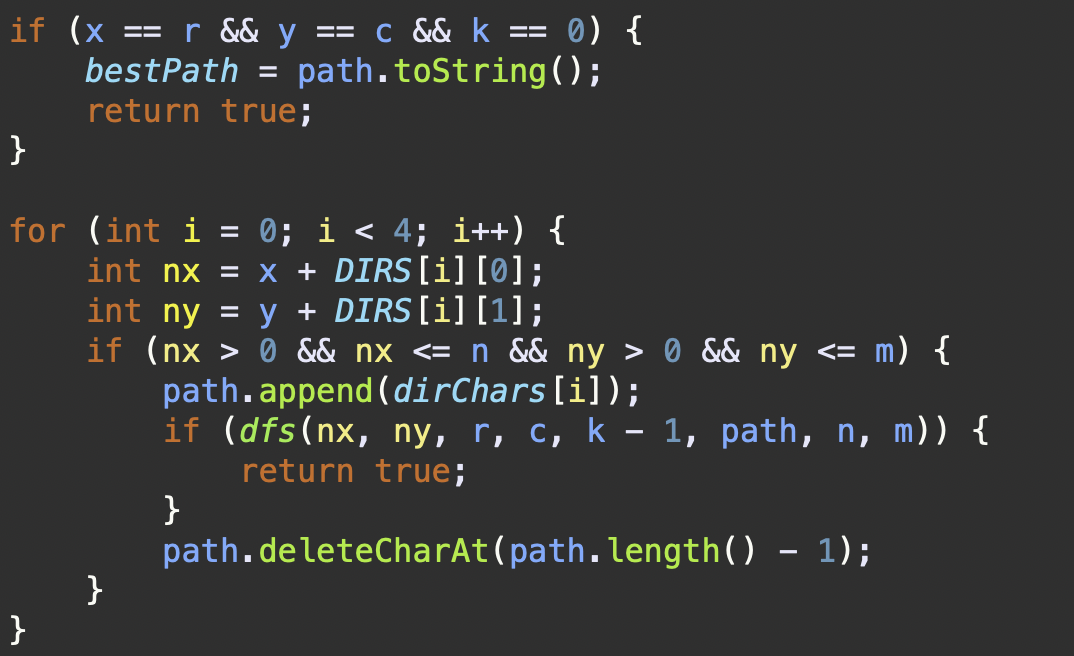
위 코드는 유효한 경로를 찾았을 때, 즉시 모든 상위 재귀 호출을 종료하고, 최적의 경로가 이미 찾아졌음을 나타낸다. 이는 탐색 과정에서 발견된 첫 번째 유효한 경로가 사전 순으로 가장 빠른 경로임을 보장한다.

DFS를 탈출할 수 있는 기저조건(base case) 두 가지

이동 가능성 검증 (if(k < remainingDistance) : 출발점에서 도착점까지의 최소 거리보다 주어진 이동 횟수 k가 작은 경우, 목적지에 도달할 수 없으므로, 더 이상 탐색은 의미가 없다.
(k - remainingDistance) % 2 != 0 조건은 탐색 알고리즘에서 가지치기(pruning)를 수행하는 데 필요한 조건으로, 특히 같은 길을 반복해서 오갈수 있는 상황을 고려한다. 이 조건은 주어진 이동 횟수 k와 목적지까지의 최소 거리인 remainingDistance 사이의 관계를 활용하여, 남은 이동 횟수를 모두 소진할 수 있는지 판단한다.

홀수 / 짝수 일치성 검증의 필요성

짝수 예시 (k = 6, remainingDistance = 4) : 목적지에 도착한 후 (remainingDistance = 4로 이동하여 목적지에 도착), 남은 이동 횟수 k가 2가 된다. 이 경우, 도착점 바로 직전으로 다시 한 번 이동했다가 목적지로 돌아올 수 있다(k = 6을 만족). 즉, 남은 이동 횟수를 정확히 소진할 수 있어, 탐색을 계속할 수 있다는 의미이다.

홀수 예시 (k = 5, remainingDistance = 4) : 목적지까지의 이동을 완료한 후 남은 이동 횟수가 1이다. 이 상황에서는 남은 이동 횟수를 정확히 사용할 방법이 없다. 도착점 바로 직전으로 다시 돌아가면 (remainingDistance = 4로 이동 후 한 번 더 이동하여 k = 5가 되지만), 다시 목적지로 돌아올 수 없다. 이 경우, 남은 이동 횟수를 효과적으로 사용할 수 없으므로, 더 이상의 탐색은 의미가 없다는 뜻이다.

이강용

HW + SW = 1

이전 포스트

Programmers #59

Programmers

`기둥과 보 설치`

`column & beam 정적 변수 선언`

`배열 크기 할당 (n+2)`

`매개변수 build_frame 순회 및 변수 초기화`

`핵심 로직 #1`

`checkColumn()`

`핵심 로직 #2`

`checkBeam()`

`canDelete()`

`결과 반환`

`광고 삽입`

`양과 늑대`

보행자 천국

미로 탈출 명령어

`DFS와 가지치기(Pruning)`

1. 첫 번째 로직의 한계

2. 두 번째 로직으로의 개선

DFS를 탈출할 수 있는 기저조건(base case) 두 가지

`홀수 / 짝수 일치성 검증의 필요성`

Programmers #58

0개의 댓글