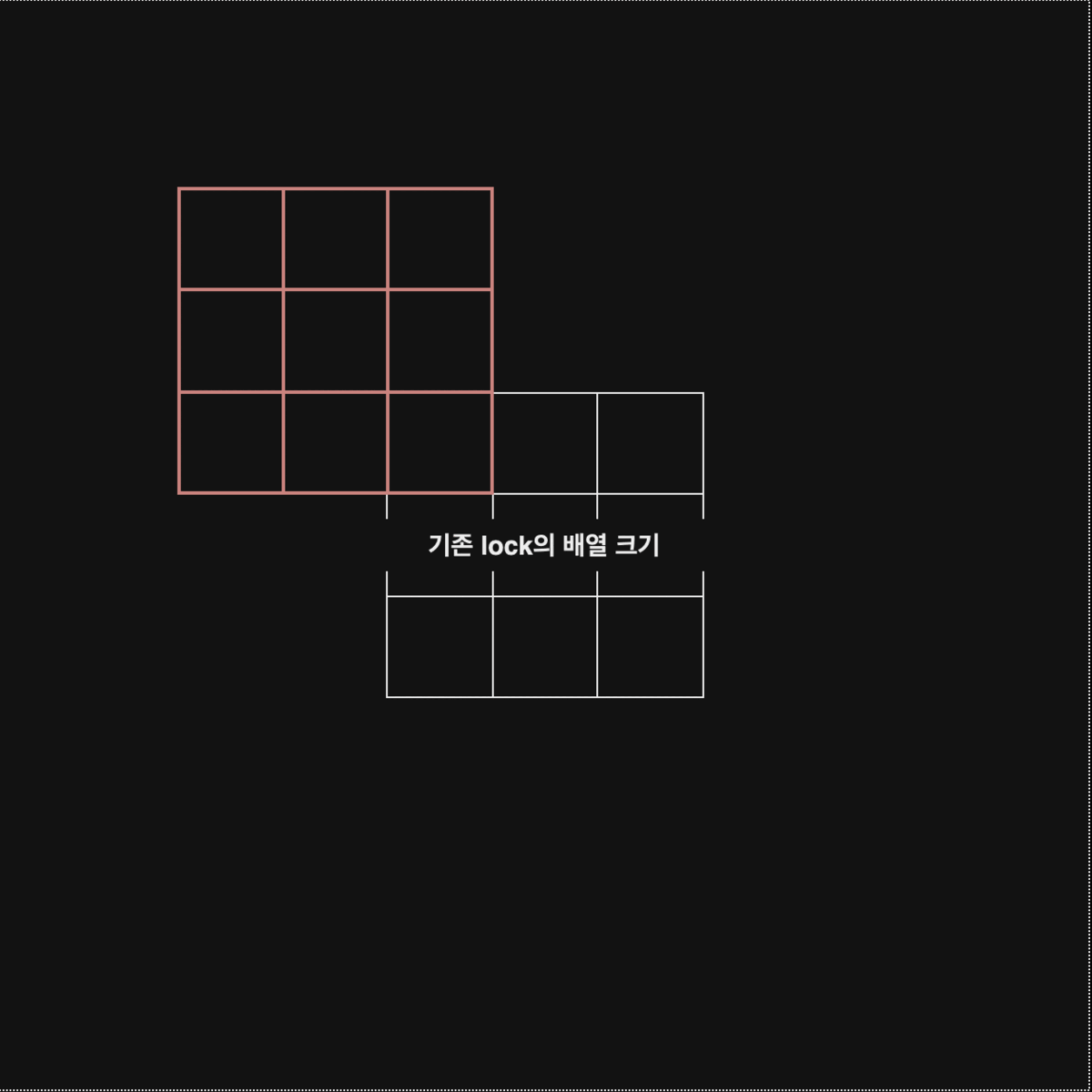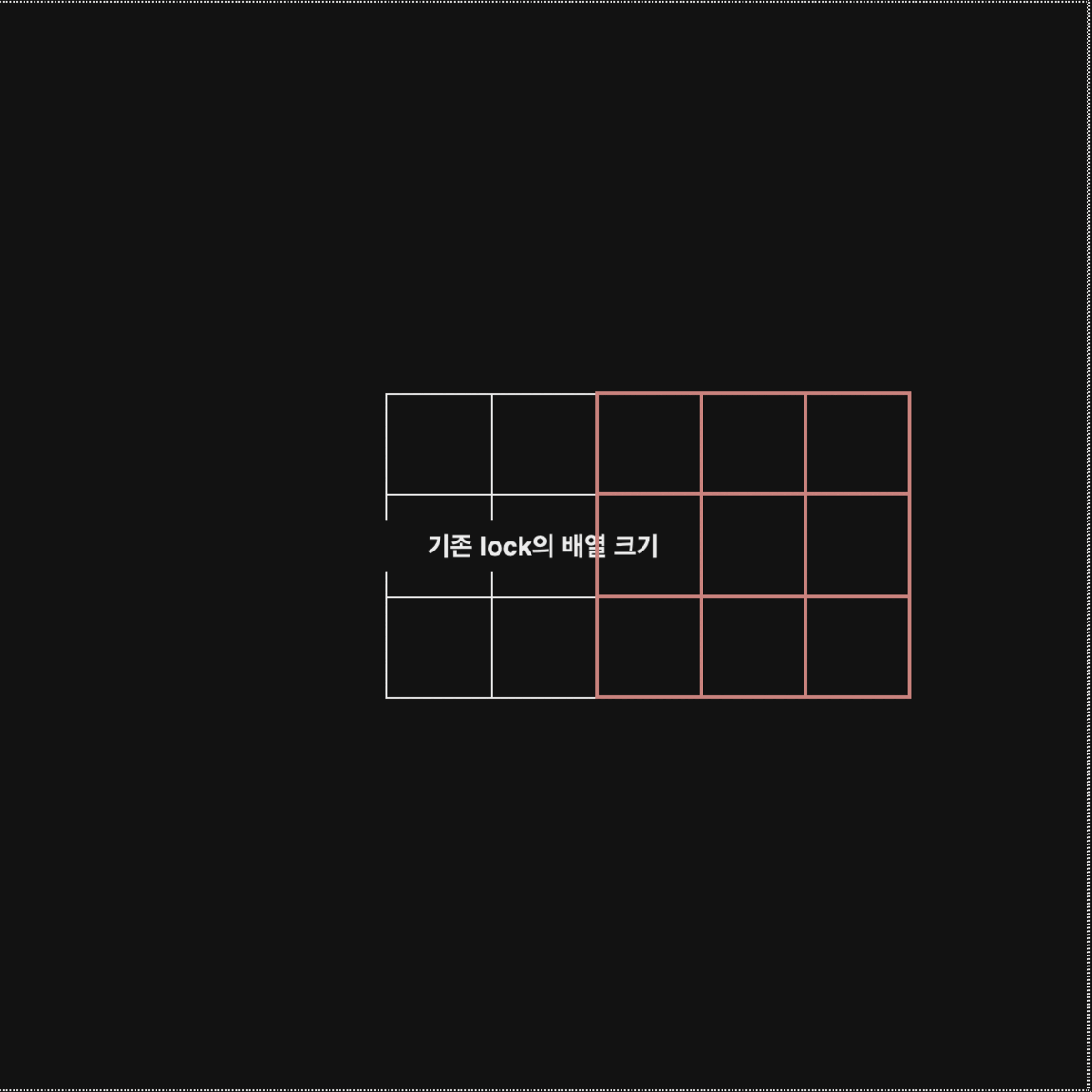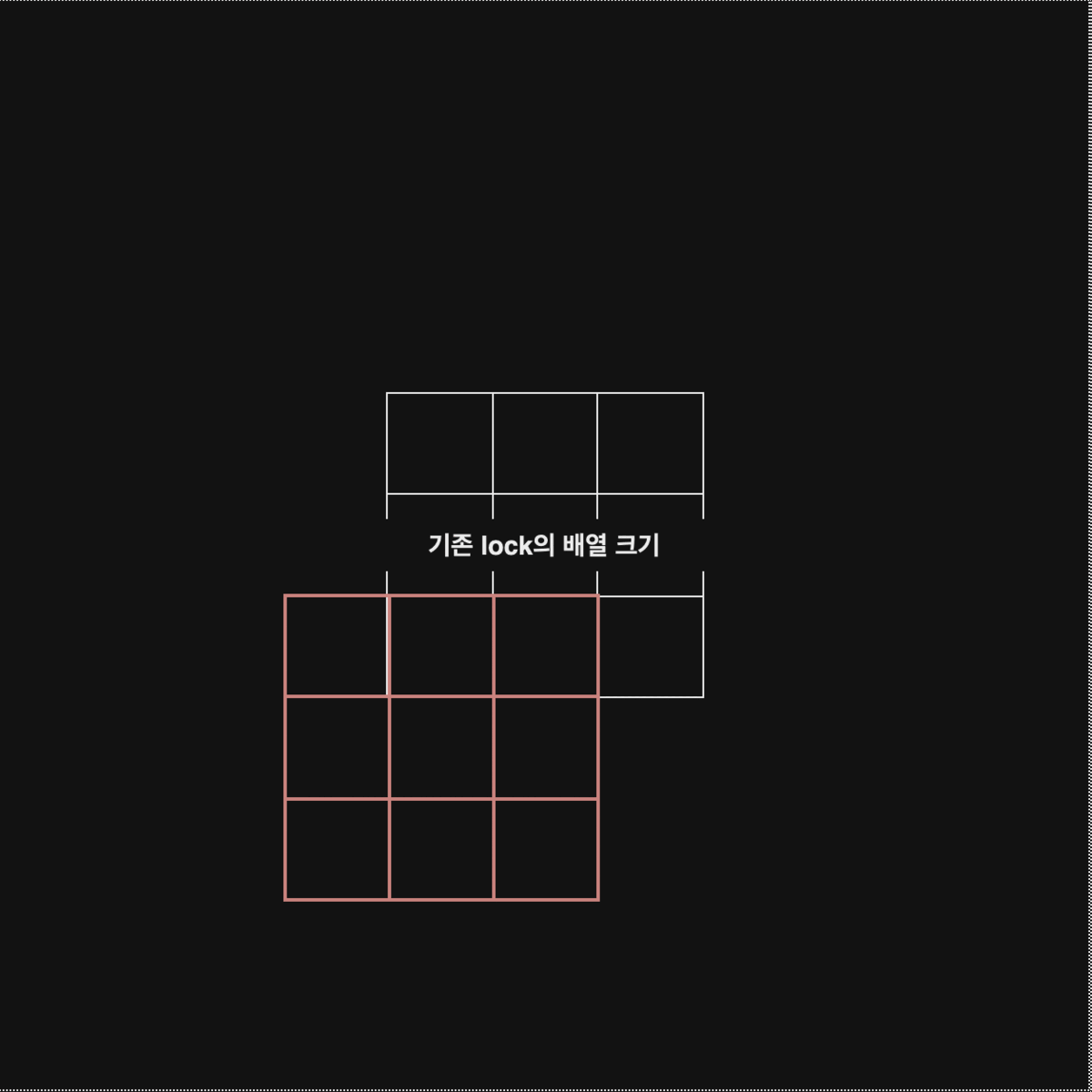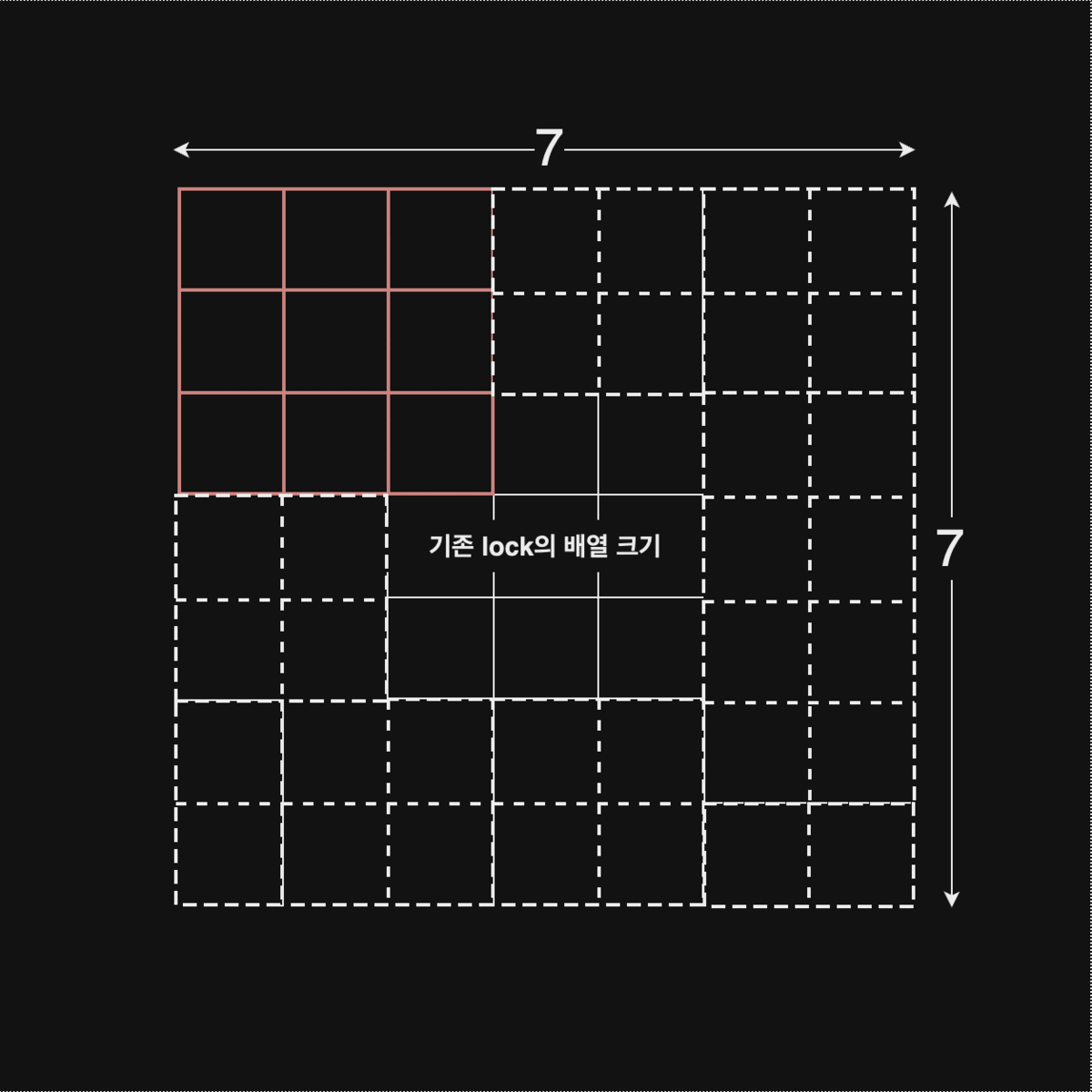Programmers #57

이강용·2024년 2월 10일

Programmers

목록 보기

56/58

풍선 터트리기

문1) 일렬로 나열된 n개의 풍선이 있습니다. 모든 풍선에는 서로 다른 숫자가 써져 있습니다. 당신은 다음 과정을 반복하면서 풍선들을 단 1개만 남을 때까지 계속 터트리려고 합니다.

임의의 인접한 두 풍선을 고른 뒤, 두 풍선 중 하나를 터트립니다.
터진 풍선으로 인해 풍선들 사이에 빈 공간이 생겼다면, 빈 공간이 없도록 풍선들을 중앙으로 밀착시킵니다.

여기서 조건이 있습니다. 인접한 두 풍선 중에서 번호가 더 작은 풍선을 터트리는 행위는 최대 1번만 할 수 있습니다. 즉, 어떤 시점에서 인접한 두 풍선 중 번호가 더 작은 풍선을 터트렸다면, 그 이후에는 인접한 두 풍선을 고른 뒤 번호가 더 큰 풍선만을 터트릴 수 있습니다.

당신은 어떤 풍선이 최후까지 남을 수 있는지 알아보고 싶습니다. 위에 서술된 조건대로 풍선을 터트리다 보면, 어떤 풍선은 최후까지 남을 수도 있지만, 어떤 풍선은 무슨 수를 쓰더라도 마지막까지 남기는 것이 불가능할 수도 있습니다.

일렬로 나열된 풍선들의 번호가 담긴 배열 a가 주어집니다. 위에 서술된 규칙대로 풍선들을 1개만 남을 때까지 터트렸을 때 최후까지 남기는 것이 가능한 풍선들의 개수를 return 하도록 solution 함수를 완성해주세요.

제한 사항

a의 길이는 1 이상 1,000,000 이하입니다.
- a[i]는 i+1 번째 풍선에 써진 숫자를 의미합니다.
- a의 모든 수는 -1,000,000,000 이상 1,000,000,000 이하인 정수입니다.
- a의 모든 수는 서로 다릅니다.

입출력 예

a	result
`[9,-1,-5]`	3
`[-16,27,65,-2,58,-92,-71,-68,-61,-33]`	6

입출력 예 설명

입출력 예 #1

첫 번째 풍선(9가 써진 풍선)을 최후까지 남기는 방법은 다음과 같습니다.
1. [9, -1, -5] 에서 -1, -5가 써진 풍선을 고른 뒤, -1이 써진 풍선(번호가 더 큰 것)을 터트립니다.
2. [9, -5] 에서 9, -5가 써진 풍선을 고른 뒤, -5가 써진 풍선(번호가 더 작은 것)을 터트립니다.
두 번째 풍선(-1이 써진 풍선)을 최후까지 남기는 방법은 다음과 같습니다.
1. [9, -1, -5] 에서 9, -1이 써진 풍선을 고른 뒤, 9가 써진 풍선(번호가 더 큰 것)을 터트립니다.
2. [-1, -5] 에서 -1, -5가 써진 풍선을 고른 뒤, -5가 써진 풍선(번호가 더 작은 것)을 터트립니다.
세 번째 풍선(-5가 써진 풍선)을 최후까지 남기는 방법은 다음과 같습니다.
1. [9, -1, -5] 에서 9, -1이 써진 풍선을 고른 뒤, 9가 써진 풍선(번호가 더 큰 것)을 터트립니다.
2. [-1, -5] 에서 -1, -5가 써진 풍선을 고른 뒤, -1이 써진 풍선(번호가 더 큰 것)을 터트립니다.
3개의 풍선이 최후까지 남을 수 있으므로, 3을 return 해야 합니다.

입출력 예 #2

최후까지 남을 수 있는 풍선은 -16, -92, -71, -68, -61, -33이 써진 풍선으로 모두 6개입니다.

나의 풀이

package programmers;

import java.util.Arrays;

public class PopTheBalloon {
	
	public static int solution(int[] a) {
        int answer = 0;
        int length = a.length;
        
        int[] leftMin = new int[length];
        int[] rightMin = new int[length];
        
        
        leftMin[0] = a[0];
        rightMin[length-1] = a[length-1];
        
        for(int i = 1; i < length; i++) {
        	leftMin[i] = Math.min(leftMin[i-1], a[i]);
        }
       
        
        
        for(int i = length - 2; i >= 0; i-- ) {
        	rightMin[i] = Math.min(rightMin[i+1], a[i]);
        }
       
        
        for(int i = 0; i < length; i++) {
        	if (i == 0 || i == length - 1 || a[i] < leftMin[i - 1] || a[i] < rightMin[i + 1]) {
                answer++;
            }
        }
        
        return answer;
    }
	
	public static void main(String[] args) {
		int[] a = {9,-1,-5};
		solution(a);
	}

}

set을 이용한 풀이법

package programmers;

import java.util.HashSet;
import java.util.Set;

public class PopTheBalloon {
	
	public static int solution(int[] a) {
        
        int leftMin = Integer.MAX_VALUE;
        int rightMin = Integer.MAX_VALUE;
        Set<Integer> set = new HashSet<>();
        
        for(int i = 0; i < a.length; i++) {
        	leftMin = Math.min(leftMin, a[i]);
        	rightMin = Math.min(rightMin, a[a.length-1-i]);
        	set.add(leftMin);
        	set.add(rightMin);
        }
        
        System.out.println(set);
        
        
        return set.size();
    }
	
	public static void main(String[] args) {
		int[] a = {-16,27,65,-2,58,-92,-71,-68,-61,-33};
		solution(a);
	}

}

나의 생각

이번 문제의 핵심은 특정 조건 하에 풍선을 터트릴 때, 어떤 풍선들이 최후까지 남을 수 있는지 파악하는 것이였다. 핵심 조건은

임의의 인전합 두 풍선 중 하나를 터트릴 수 있다.

번호가 더 작은 풍선을 터트리는 행위는 최대 한 번만 허용된다.

이 규칙들로, 각 풍선이 마지막까지 남을 수 있는지 여부를 결정하는 핵심 요소는 그 풍선이 위치한 곳의 양쪽에 있는 풍선들의 번호이다.

자신보다 작은 풍선을 터트리는 기회를 언제 사용할 것인가?

이 기회는 매우 중요하며, 특정 풍선을 최후까지 남기기 위해 전략적으로 사용해야한다.
만약 어떤 풍선이 자신의 왼쪽과 오른쪽에 모두 자신보다 작은 번호의 풍선이 있다면, 그 풍선은 최후까지 남을 수 없다.(기회를 이미 사용했다고 가정할 때) 왜냐하면 두 방향 모두에서 작은 풍선을 터트려야 하기 때문(~~불가능~~)

양쪽 방향에서의 최소값을 알아내는 것

각 풍선 위치에서 왼쪽 방향으로의 최소값과 오른쪽 방향으로의 최소값을 알면, 그 위치의 풍선이 최후까지 남을 수 잇는지 판단할 수 있음
어떤 위치의 풍선이 그 위치에서 왼쪽 방향의 최소값보다 크고 오른쪽 방향의 최소값보다도 크다면, 그 풍선은 최후까지 남을 수 없음. 왜냐하면 양쪽에서 더 작은 풍선을 최소 한 번 이상 터트려야 하기 때문
반대로, 어떤 위치의 풍선이 왼쪽 또는 오른쪽 방향의 최소값보다 작다면, 그 풍선은 최후까지 남을 수 있음. 그 방향에서 더 작은 풍선을 터트릴 필요가 없기 떄문

부대복귀

문2) 강철부대의 각 부대원이 여러 지역에 뿔뿔이 흩어져 특수 임무를 수행 중입니다. 지도에서 강철부대가 위치한 지역을 포함한 각 지역은 유일한 번호로 구분되며, 두 지역 간의 길을 통과하는 데 걸리는 시간은 모두 1로 동일합니다. 임무를 수행한 각 부대원은 지도 정보를 이용하여 최단시간에 부대로 복귀하고자 합니다. 다만 적군의 방해로 인해, 임무의 시작 때와 다르게 되돌아오는 경로가 없어져 복귀가 불가능한 부대원도 있을 수 있습니다.

강철부대가 위치한 지역을 포함한 총지역의 수 n, 두 지역을 왕복할 수 있는 길 정보를 담은 2차원 정수 배열 roads, 각 부대원이 위치한 서로 다른 지역들을 나타내는 정수 배열 sources, 강철부대의 지역 destination이 주어졌을 때, 주어진 sources의 원소 순서대로 강철부대로 복귀할 수 있는 최단시간을 담은 배열을 return하는 solution 함수를 완성해주세요. 복귀가 불가능한 경우 해당 부대원의 최단시간은 -1입니다.

제한 사항

3 ≤ n ≤ 100,000
- 각 지역은 정수 1부터 n까지의 번호로 구분됩니다.
2 ≤ roads의 길이 ≤ 500,000
- roads의 원소의 길이 = 2
- roads의 원소는 [a, b] 형태로 두 지역 a, b가 서로 왕복할 수 있음을 의미합니다.(1 ≤ a, b ≤ n, a ≠ b)
- 동일한 정보가 중복해서 주어지지 않습니다.
  - 동일한 [a, b]가 중복해서 주어지지 않습니다.
  - [a, b]가 있다면 [b, a]는 주어지지 않습니다.
1 ≤ sources의 길이 ≤ 500
- 1 ≤ sources[i] ≤ n
1 ≤ destination ≤ n

입출력 예

n	roads	sources	destination	result
3	`[[1,2],[2,3]]`	`[2,3]`	1	`[1,2]`
5	`[[1, 2], [1, 4], [2, 4], [2, 5], [4, 5]]`	`[1, 3, 5]`	5	`[2, -1, 0]`

입출력 예 설명

입출력 예 #1

지역 2는 지역 1과 길로 연결되어 있기 때문에, 지역 2에서 지역 1의 최단거리는 1입니다.
지역 3에서 지역 1로 이동할 수 있는 최단경로는 지역 3 → 지역 2 → 지역 1 순으로 이동하는 것이기 때문에, 지역 3에서 지역 1의 최단거리는 2입니다.
따라서 [1, 2]를 return합니다.

입출력 예 #2

지역 1에서 지역 5의 최단경로는 지역 1 → 지역 2 → 지역 5 또는 지역 1 → 지역 4 → 지역 5 순으로 이동하는 것이기 때문에, 최단거리는 2입니다.
지역 3에서 지역 5로 가는 경로가 없기 때문에, 지역 3에서 지역 5로 가는 최단거리는 -1입니다.
지역 5에서 지역 5는 이동할 필요가 없기 때문에, 최단거리는 0입니다.
따라서 [2, -1, 0]을 return합니다.

나의 풀이

플로이드 와샬 알고리즘으로 접근한 풀이(시간 초과)

package programmers;

import java.util.Arrays;

public class ReturnToUnit {
	
	public static final int INF = 10_000_000;
	
	public static int[] solution(int n, int[][] roads, int[] sources, int destination) {
        
        int[][] graph = new int[n+1][n+1];
        
        for(int i = 1; i <= n; i++) {
        	for(int j = 1; j <= n; j++) {
        		if(i == j) graph[i][j] = 0;
        		else graph[i][j] = INF;
        	}
        }
        
       for(int[] road : roads) {
    	   int x = road[0];
    	   int y = road[1];
    	   
    	   graph[x][y] = 1;
    	   graph[y][x] = 1;
       }
       
       for(int k = 1; k <= n; k++) {
    	   for(int i = 1; i <= n; i++) {
    		   for(int j = 1; j <= n; j++) {
    			   if(graph[i][k] != INF && graph[k][j] != INF) {
    				   graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
    			   }
    		   }
    	   }
       }
        
       
       for(int[] a : graph) {
    	   System.out.println(Arrays.toString(a));
       }
       int[] answer = new int[sources.length];
       
       for (int i = 0; i < answer.length; i++) {
    	    answer[i] = (graph[destination][sources[i]] == INF) ? -1 : graph[destination][sources[i]];
    	}

        
       System.out.println(Arrays.toString(answer)); 
       return answer;
    }
	
	public static void main(String[] args) {
		
		int[][] roads = {{1,2},{1,4},{2,4},{2,5},{4,5}};
		int[] sources = {1,3,5};
		
		solution(5, roads, sources, 5);
		
	}

}

다익스트라(Dijkstra) 알고리즘 우선순위 큐로 구현

java

import java.util.*;

class Solution {
    public static final int INF = 10_000_000;

    public static int[] solution(int n, int[][] roads, int[] sources, int destination) {
        ArrayList<ArrayList<Node>> graph = new ArrayList<>();
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<>());
        }

        for (int[] road : roads) {
            int a = road[0];
            int b = road[1];
            graph.get(a).add(new Node(b, 1));
            graph.get(b).add(new Node(a, 1));
        }

        int[] shortestPaths = dijkstra(graph, destination, n);

        int[] answer = new int[sources.length];
        for (int i = 0; i < sources.length; i++) {
            int distance = shortestPaths[sources[i]];
            answer[i] = distance == INF ? -1 : distance;
        }

        return answer;
    }

    public static int[] dijkstra(ArrayList<ArrayList<Node>> graph, int start, int n) {
        int[] distances = new int[n + 1];
        Arrays.fill(distances, INF);
        distances[start] = 0;
        PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a.cost));
        pq.offer(new Node(start, 0));

        while (!pq.isEmpty()) {
            Node current = pq.poll();
            int currentNode = current.vertex;
            int currentDistance = current.cost;

            if (distances[currentNode] < currentDistance) {
                continue;
            }

            for (Node node : graph.get(currentNode)) {
                int cost = currentDistance + node.cost;
                if (cost < distances[node.vertex]) {
                    distances[node.vertex] = cost;
                    pq.offer(new Node(node.vertex, cost));
                }
            }
        }

        return distances;
    }

    static class Node {
        int vertex;
        int cost;

        Node(int vertex, int cost) {
            this.vertex = vertex;
            this.cost = cost;
        }
    }

    public static void main(String[] args) {
        int[][] roads = {{1, 2}, {1, 4}, {2, 4}, {2, 5}, {4, 5}};
        int[] sources = {1, 3, 5};

        int[] result = solution(5, roads, sources, 5);
        System.out.println(Arrays.toString(result)); // 출력: [2, -1, 0]
    }
}

나의 생각

👉🏻 다익스트라 알고리즘 개념

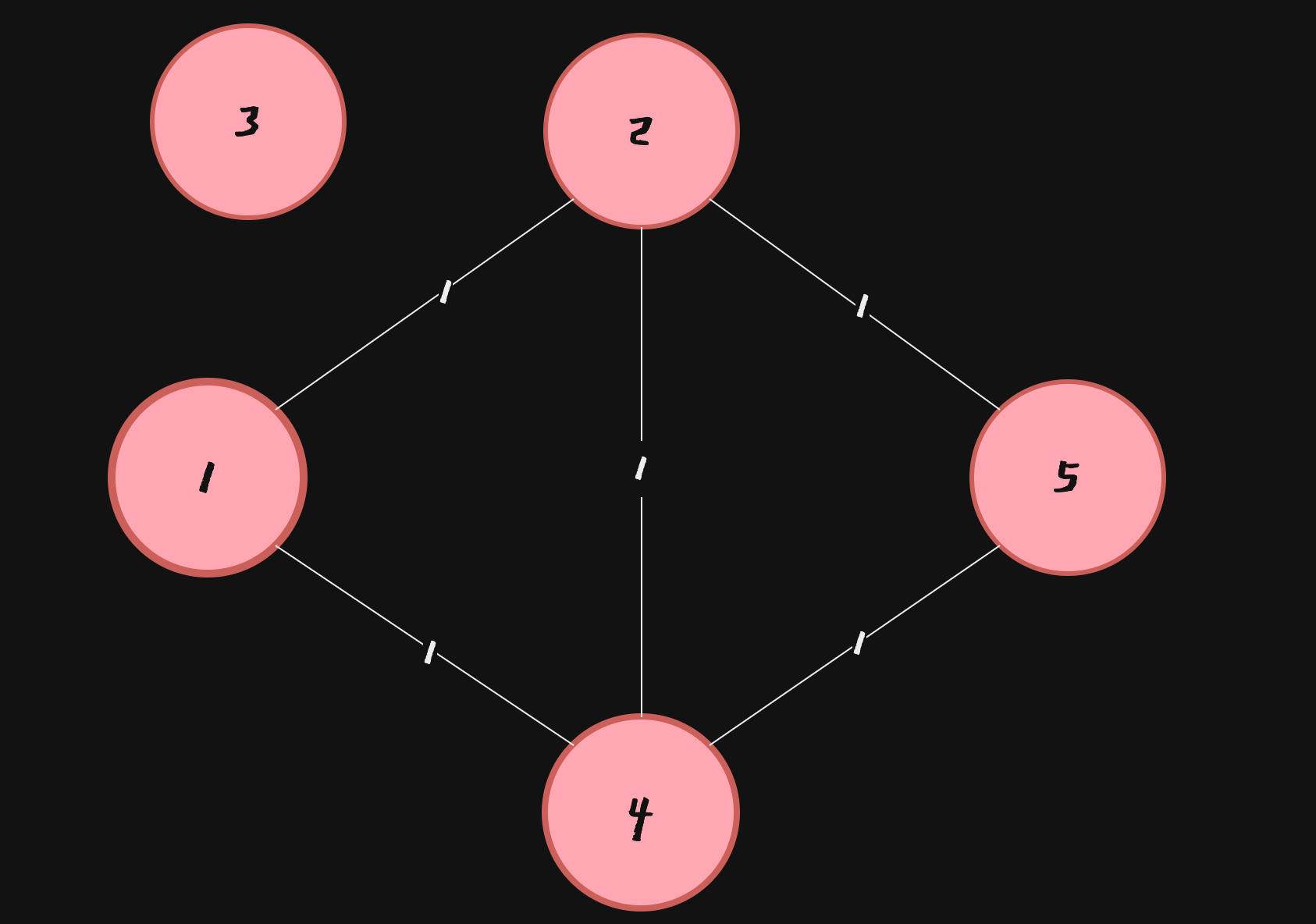
node 1 : (2,1) , (4,1)
node 2 : (1,1), (4,1), (5,1)
node 3 : X
node 4 : (1,1), (2,1), (5,1)
node 5 : (2,1), (4,1)

> 여기서 (2,1)은 Node 2까지 비용이 1이라는 의미이다

초기설정

distance 배열을 INF로 초기화하고, 시작점인 노드 5의 거리는 0으로 설정

우선순위 큐 pq에 시작 노드 5를 (노드 번호, 비용) 쌍으로 추가함
👉🏻 pq.offer(new Node(5,0))

다익스트라 알고리즘 순서

처음 상태 :

pq : [(5,0)]

distance :[INF,INF,INF,INF,0]

Node 5 처리 :

pq.poll()로 (5,0)을 꺼냄

노드 5에 인접한 노드는 2와 4임. 이들의 거리를 갱신하고 우선순위 큐에 추가

노드 2의 거리를 1로 갱신하고 큐에 추가 : pq.offer(new Node(2,1))

노드 4의 거리를 1로 갱신하고 큐에 추가 : pq.offer(new Node(4,1))

pq : [(2,1),(4,1)]

distance : [INF,1,INF,1,0]

Node 2 처리 :

pq.poll()로 (2,1)을 꺼냄

노드 2에 인접한 노드는 1,4,5임. 노드 5는 이미 처리됐으므로 무시함

노드 1의 거리를 2로 갱신하고 큐에 추가 : pq.offer(new Node(1,2))

노드 5 → 노드 4 기존 비용 1, 노드 5 → 노드 2 → 노드 4 비용이 2이기때문에 기존 비용이 더 최소값이기 때문에 갱신하지 않음

pq : [(4,1),(2,1)]

distance : [2,1,INF,1,0]

Node 4 처리 :

pq.poll()로 (4,1)을 꺼냄

노드 4에 인접한 노드는 1,2,5임. 노드 5와 노드2는 이미 처리되엇거나 대기 중이므로 무시

노드 1의 현재 거리는 2이고, 노드 4를 거쳐갈 경우의 거리도 2(노드 5 → 노드 4 → 노드 1 = 1+1)이므로 갱신하지 않음

pq : [(1,2)]

distance : [2,1,INF,1,0]

Node 1 처리 :

pq.poll()로 (1,2)를 꺼냄

노드 1에 인접한 노드는 2와 4임. 이들은 이미 처리되었거나 처리 대기 중이므로 무시

pq : []

distance : [2,1,INF,1,0]

최종 거리 배열

문제에서 원하는 결과값은 sources[i]에서 목적지까지의 최단 거리 이기때문에
sources = {1,3,5}라 할때,
int distance = shortestPaths[1,3,5] 값이 들어간다.
distance = 2, INF, 0이 되는데, INF는 최단 거리가 없단 의미로 -1을 따로 반환해주면 된다.
따라서, 최종 answer 배열의 결과는 ✍🏻 [2,-1,0]

인사고과

문3) 완호네 회사는 연말마다 1년 간의 인사고과에 따라 인센티브를 지급합니다. 각 사원마다 근무 태도 점수와 동료 평가 점수가 기록되어 있는데 만약 어떤 사원이 다른 임의의 사원보다 두 점수가 모두 낮은 경우가 한 번이라도 있다면 그 사원은 인센티브를 받지 못합니다. 그렇지 않은 사원들에 대해서는 두 점수의 합이 높은 순으로 석차를 내어 석차에 따라 인센티브가 차등 지급됩니다. 이때, 두 점수의 합이 동일한 사원들은 동석차이며, 동석차의 수만큼 다음 석차는 건너 뜁니다. 예를 들어 점수의 합이 가장 큰 사원이 2명이라면 1등이 2명이고 2등 없이 다음 석차는 3등부터입니다.

각 사원의 근무 태도 점수와 동료 평가 점수 목록 scores이 주어졌을 때, 완호의 석차를 return 하도록 solution 함수를 완성해주세요.

제한 사항

1 ≤ scores의 길이 ≤ 100,000
scores의 각 행은 한 사원의 근무 태도 점수와 동료 평가 점수를 나타내며 [a, b] 형태입니다.
- scores[0]은 완호의 점수입니다.
- 0 ≤ a, b ≤ 100,000
완호가 인센티브를 받지 못하는 경우 -1을 return 합니다.

입출력 예

scores	result
`[[2,2],[1,4],[3,2],[3,2],[2,1]]`	4

입출력 예 설명

5 번째 사원은 3 번째 또는 4 번째 사원보다 근무 태도 점수와 동료 평가 점수가 모두 낮기 때문에 인센티브를 받을 수 없습니다. 2 번째 사원, 3 번째 사원, 4 번째 사원은 두 점수의 합이 5 점으로 최고점이므로 1 등입니다. 1 등이 세 명이므로 2 등과 3 등은 없고 1 번째 사원인 완호는 두 점수의 합이 4 점으로 4 등입니다.

나의 풀이

package programmers;

import java.util.Arrays;

public class PerformanceReview {
	
	public static int solution(int[][] scores) {
		int[] wanHo = scores[0];
		Arrays.sort(scores, (a,b) -> a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]);
		
		int answer = 1;
		int maxScore = 0;
		int wanHoSum = wanHo[0] + wanHo[1];
		
		for (int[] score : scores) {
            
            if (score[1] < maxScore) {
              
                if (Arrays.equals(score, wanHo))
                    return -1;
            } else {
               
                maxScore = score[1];
                if (score[0] + score[1] > wanHoSum)
                    answer++;
            }
        }
        System.out.println(answer);
        return answer;
    }
	
	public static void main(String[] args) {
		int[][] scores = {{2,2},{1,4},{3,2},{3,2},{2,1}};
		solution(scores);
	}

}

자물쇠와 열쇠

문4) 고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.

잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.

자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.

열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.

제한사항

key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
M은 항상 N 이하입니다.
key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
- 0은 홈 부분, 1은 돌기 부분을 나타냅니다.

입출력 예

key	lock	result
`[[0, 0, 0], [1, 0, 0], [0, 1, 1]]`	`[[1, 1, 1], [1, 1, 0], [1, 0, 1]]`	true

입출력 예 설명

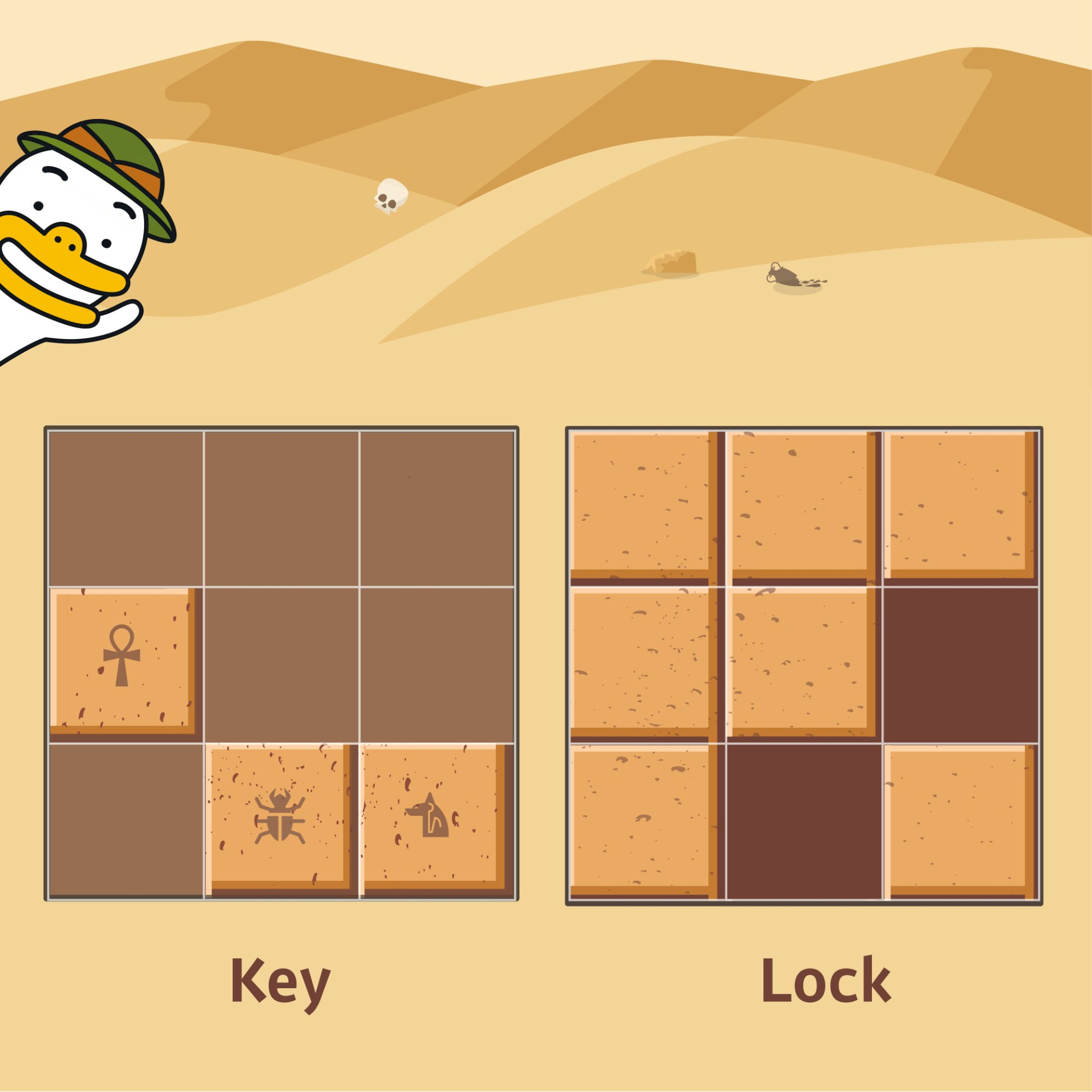
나의 풀이

package programmers;

public class LockAndKey {
	
	public static int[][] rotate(int[][] matrix){
		int m = matrix.length;
		int n = matrix[0].length;
		int[][] rotated = new int[n][m];
		
		for(int i = 0; i < m; i++) {
			for(int j = 0; j < n; j++) {
				rotated[j][m - 1 - i] = matrix[i][j];
			}
		}
		
		return rotated;
	}
	
	public static boolean check(int[][] largeLock, int[][] key, int startRow, int startCol) {
	    int N = largeLock.length - (2 * (key.length - 1));
	    int M = key.length;
	    int offset = M - 1;

	    for (int i = 0; i < M; i++) {
	        for (int j = 0; j < M; j++) {
	            largeLock[startRow + i][startCol + j] += key[i][j];
	        }
	    }

	    for (int i = offset; i < offset + N; i++) {
	        for (int j = offset; j < offset + N; j++) {
	            if (largeLock[i][j] != 1) {
	               
	                for (int x = 0; x < M; x++) {
	                    for (int y = 0; y < M; y++) {
	                        largeLock[startRow + x][startCol + y] -= key[x][y];
	                    }
	                }
	                return false;
	            }
	        }
	    }

	    

	    return true;
	}
	
	
	
	public static boolean solution(int[][] key, int[][] lock) {
        
		int N = lock.length; 
		int M = key.length;
		int extendedSize = N + 2 * (M - 1);
        int[][] largeLock = new int[extendedSize][extendedSize];
        
        for(int i = 0; i < N; i++) {
        	for(int j = 0; j < N; j++) {
        		largeLock[i + M - 1][j + M - 1] = lock[i][j];
        	}
        }
        
       for(int r = 0; r < 4; r++) {
    	   key = rotate(key);
    	   for(int x = 0; x <= extendedSize - M; x++) {
    		   for(int y = 0; y <= extendedSize - M; y++) {
    			   if(check(largeLock, key, x, y)) {
    				   return true;
    			   }
    		   }
    	   }
       
       
       }
       
        return false;
    }
	
	
	public static void main(String[] args) {
		int[][] key = {{0,0,0},{1,0,0},{0,1,1}};
		int[][] lock = {{1,1,1},{1,1,0},{1,0,1}};
		solution(key, lock);
	}

}

나의 생각

이번 문제를 보면서 해결해야하는 몇 가지 부분을 먼저 살펴보았다.

lock 배열 확장하기 : 자물쇠 배열(lock)을 확장하여 열쇠(key)가 자물쇠 영역 밖으로 이동 할 수 있게 하면서도 자물쇠의 홈 부분에 정확히 맞출 수 있도록 한다.
👉🏻 확장된 lock 배열 크기를 정하는 방법

열쇠 회전 : 열쇠(key)를 90도 단위로 회전시켜 모든 가능한 방향에서 자물쇠(lock)의 홈과 맞출 수 있도록 한다.
👉🏻 배열 전체를 네 가지 방향(0도, 90도, 180도, 270도)으로 회전하는 방법

열쇠 이동 : 회전된 열쇠를 자물쇠의 확장된 영역 내에서 모든 가능한 위치로 이동시켜 보며, 열쇠의 돌기 부분이 자물쇠의 홈 부분에 정확히 들어맞는지 확인한다.
👉🏻 열쇠의 돌기 부분과 자물쇠의 홈 부분의 일치 여부 확인 방법

매칭 검사 : 열쇠를 회전시키고 이동시킨후, 자물쇠의 모든 홈이 열쇠의 돌기 부분으로 정확히 채워지는지 검사한다. 이 때, 자물쇠 영역 내에서는 열쇠의 홈과 돌기가 겹치지 않아야 하며, 자물쇠의 모든 홈이 채워져야 한다.

성공 조건 판별 : 위의 조건들을 모두 만족하는 경우(자물쇠의 모든 홈이 채워질 때), 함수는 true를 반환, 아니면 false를 반환

1. lock 배열 확장하기

문제의 예시를 보면 아래와 같은 그림을 먼저 보자.

int[][] key = {{0,0,0},{1,0,0},{0,1,1}};
int[][] lock = {{1,1,1},{1,1,0},{1,0,1}};
즉, key와 lock의 size는 3이다.

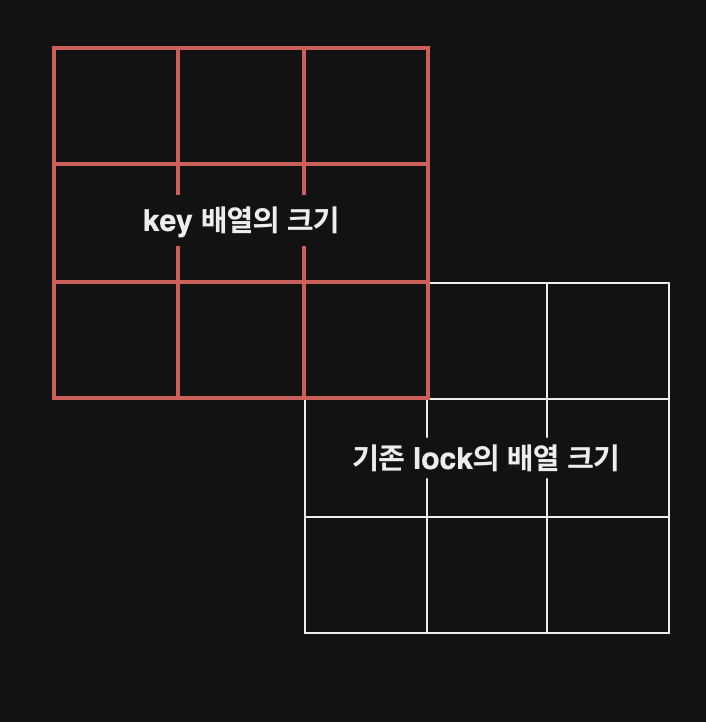
기존의 lock 배열의 좌측 상단 모서리 부분에 크기3인 key 배열이 온다면 다음과 같다.
기존의 lock 배열의 가장자리 부분을 key배열이 걸쳐서 이동한다면 다음과 같다.
따라서, 기존의 배열크기 3에서 확장된 배열의 크기는 7이다.
- 이것을 식으로 유도하면 다음과 같다. $int extendedSize = N + 2 * (M - 1);$

세로 길이만 보면, 기존의 배열의 크기 N + (위, 아래 총 2개) 2 * (key의 배열 크기 - 1) 만큼 확장하였기 때문이다.

2. largeLock 중간 부분을 lock의 값으로 채우기

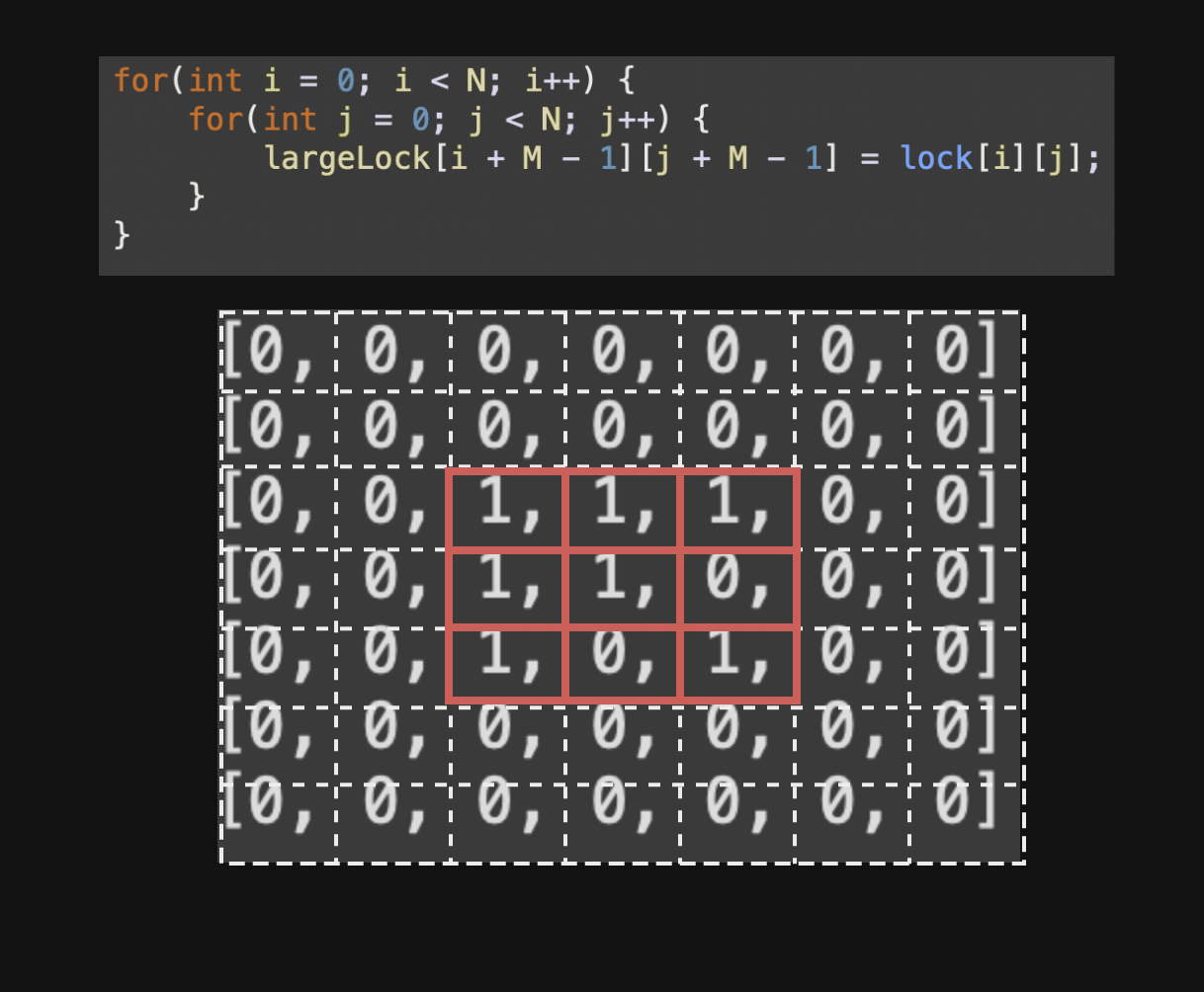
3. 열쇠 회전

예를들어, 1부터 9까지 숫자가 포함된 2차원 배열이 있다. 이를 90도로 오른쪽으로 회전시키면 그림과 같은 형태가 된다.

먼저 1의 위치를 보면 
(0,0) → (0,2) 위치로 이동
(0,1) → (1,2) 위치로 이동
(0,2) → (2,2) 위치로 이동
를 보면, 원본 행렬의 행이 회전된 행렬의 열이 되는 규칙을 찾을 수 있다.
👉🏻 즉, 원본 행렬의 (i, j) 위치에 있던 요소는 회전된 행렬에서 (j, ?)의 형태를 갖는다.

(1,0) → (0,1) 위치로 이동
(1,1) → (1,1) 위치로 이동
(1,2) → (2,1) 위치로 이동
를 보면, 마찬가지로 원본 행렬의 행이 회전된 행렬의 열이 된다. 
👉🏻 즉, 원본 행렬의 최상단 행이 회전된 행렬에서는 가장 오른쪽 열로, 
 그리고 원본 행렬의 하단 행이 회전된 행렬에서는 가장 왼쪽 열로 이동함을 알 수 있다.

이를 변환식으로 나타내면 다음과 같다.

rotated[j][m - 1 - i] = matrix[i][j];

따라서

for(int r = 0; r < 4; r++) {
    	   key = rotate(key);
           
           ・
           ・
           ・
           ・
}

r값에 따라, 2차원 배열 key가 rotate배열의 매개변수로 들어가면서
key값에 각 반복마다 90도씩 회전한 배열의 값이 들어가게 된다.

4. 열쇠 이동

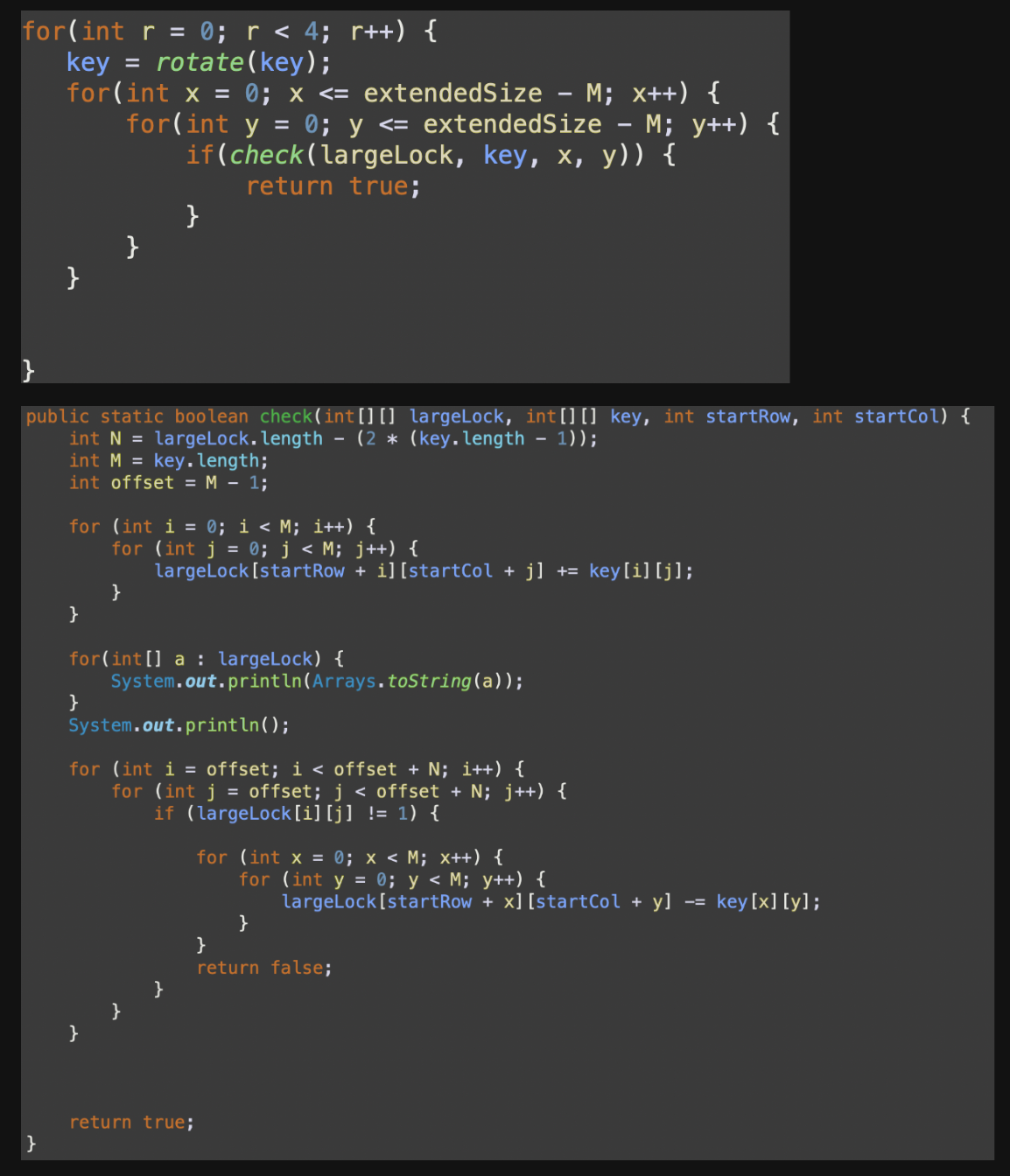
for(int x = 0; x <= extendedSize - M; x++) {
	for(int y = 0; y <= extendedSize - M; y++) {
    	if(check(largeLock, key, x, y)) {
        	return true;
        }
    }
}

위 로직을 먼저보면 x,y의 범위를 extendedSize - M 으로 하고 있는데 2차원 배열 largeLock에서 index를 0 ~ extendedSize - M만 확인하면 범위를 초과하지 않고 모든 자물쇠 영역을 확인할 수 있기때문이다.
아래의 그림을 보자

따라서, extendedSize - M 까지 범위를 설정하면 largeLock의 모든 값을 확인할 수 있다는 의미이다.

check Method()

핵심을 설명한 로직은 다음과 같다.

public static boolean check(int[][] largeLock, int[][] key, int startRow, int startCol) {
   
    int N = largeLock.length - (2 * (key.length - 1));
    int M = key.length;
    // offset은 확장된 자물쇠에서 실제 자물쇠 부분이 시작하는 인덱스
    int offset = M - 1;

   
    // 열쇠를 확장된 자물쇠에 더하는 과정
    // 열쇠 배열을 확장된 자물쇠 격자의 startRow, startCol 위치에 맞춰 더함
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < M; j++) {
            largeLock[startRow + i][startCol + j] += key[i][j];
        }
    }

    // 확장된 자물쇠의 실제 자물쇠 부분을 검사
    for (int i = offset; i < offset + N; i++) {
        for (int j = offset; j < offset + N; j++) {
            // 자물쇠의 돌기와 열쇠의 돌기가 겹치거나 홈이 채워지지 않았으면 false 반환
            if (largeLock[i][j] != 1) {
                // 검사가 실패했으므로 열쇠를 더한 부분을 다시 빼서 원상태로 복구
                for (int x = 0; x < M; x++) {
                    for (int y = 0; y < M; y++) {
                        largeLock[startRow + x][startCol + y] -= key[x][y];
                    }
                }
                return false; // 검사 실패
            }
        }
    }
    // 모든 검사를 통과했으면 true 반환
    return true;
}

이 로직은 largeLock 배열의 값을 바탕으로, key 배열을 largeLock 배열에 더해주는데,
이 로직의 핵심은 원본 lock 배열의 위치(3 X 3)에 모든 값이 1로 채워져있으면 자물쇠의 홈과, key의 돌기가 완벽하게 일치함을 의미한다. 이 경우만 true를 반환하고, 나머지 경우는 모두 false처리와 동시에, 검사가 실패했으므로 열쇠를 더한 부분을 다시 빼서 원상태로 복구하는 방식으로 로직을 구성하였다.

N으로 표현

문5) 아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.

12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5

5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.

제한 사항

N은 1 이상 9 이하입니다.
number는 1 이상 32,000 이하입니다.
수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
최솟값이 8보다 크면 -1을 return 합니다.

입출력 예

N	number	return
5	12	4
2	11	3

입출력 예 설명

예제 #2

11 = 22 / 2와 같이 2를 3번만 사용하여 표현할 수 있습니다.

나의 풀이

package programmers;

import java.util.HashSet;
import java.util.Set;

public class ExpressedAsN {
	
	public static int solution(int N, int number) {
		if(N == number) return 1;
		
		Set<Integer>[] dp = new Set[9];
		int t = N;
		
		
		for(int i = 1; i < 9; i++) {
			dp[i] = new HashSet<>();
			dp[i].add(t);
			t = t * 10 + N;
		}
		
		for(int i = 1; i < 9; i++) {
			for(int j = 1; j < i; j++) {
				for(Integer a : dp[j]) {
					for(Integer b : dp[i - j]) {
						dp[i].add(a + b);
						dp[i].add(a - b);
						dp[i].add(b - a);
						dp[i].add(a * b);
						if(b != 0) {
							dp[i].add(a/b);
						}
						if(a != 0) {
							dp[i].add(b/a);
						}
					}
				}
			}
		
			
			if (dp[i].contains(number)) {
				
                return i;
            }
		}
		
		
		return -1;
    }
	
	public static void main(String[] args) {
		solution(2, 11);
	}

}

이강용

HW + SW = 1

이전 포스트

Programmers #56

다음 포스트

Programmers #57

Programmers

풍선 터트리기

부대복귀

인사고과

자물쇠와 열쇠

N으로 표현

Programmers #56

Programmers #58

0개의 댓글