거스름돈
문1) Finn은 편의점에서 야간 아르바이트를 하고 있습니다. 야간에 손님이 너무 없어 심심한 Finn은 손님들께 거스름돈을 n 원을 줄 때 방법의 경우의 수를 구하기로 하였습니다.
예를 들어서 손님께 5원을 거슬러 줘야 하고 1원, 2원, 5원이 있다면 다음과 같이 4가지 방법으로 5원을 거슬러 줄 수 있습니다.
- 1원을 5개 사용해서 거슬러 준다.
- 1원을 3개 사용하고, 2원을 1개 사용해서 거슬러 준다.
- 1원을 1개 사용하고, 2원을 2개 사용해서 거슬러 준다.
- 5원을 1개 사용해서 거슬러 준다.
거슬러 줘야 하는 금액 n과 Finn이 현재 보유하고 있는 돈의 종류 money가 매개변수로 주어질 때, Finn이 n 원을 거슬러 줄 방법의 수를 return 하도록 solution 함수를 완성해 주세요.
제한 사항
- n은 100,000 이하의 자연수입니다.
- 화폐 단위는 100종류 이하입니다.
- 모든 화폐는 무한하게 있다고 가정합니다.
- 정답이 커질 수 있으니, 1,000,000,007로 나눈 나머지를 return 해주세요.
입출력 예
| n | money | result |
|---|---|---|
| 5 | [1,2,5] | 4 |
입출력 예 설명
- 문제의 예시와 같음
나의 풀이
package programmers;
import java.util.Arrays;
public class Change {
public static int solution(int n, int[] money) {
int[] dp = new int[n+1];
dp[0] = 1;
for(int coin : money) {
for(int amount = coin; amount <= n; amount++) {
dp[amount] += dp[amount - coin];
dp[amount] %= 1_000_000_007;
}
}
return dp[n];
}
public static void main(String[] args) {
int[] money = {1,2,5};
solution(5, money);
}
}
나의 생각
우리가 흔히 알고 있는 거스름돈 관련 문제들은 보통 거슬러 줄 수 있는 최소 동전의 개수를 찾는 문제가 일반적이다. 이 경우, 탐욕법으로 적용할 수 있지만 이번 문제는 최소 동전의 개수를 찾는 문제가 아닌, 거슬러 줄 수 있는 방법의 수를 묻는 문제였다.
문제의 예시처럼 손님께 5원을을 거슬러줘야 하고, 1원,2원, 5원이 있다면 거슬러 줄 수 있는 방법은 몇 가지일까를 생각해보면
- 1원 짜리 5개
- 1원 짜리 3개, 2원 짜리 1개
- 1원 짜리 1개, 2원 짜리 2개
- 5원 짜리 1개
총 네 가지의 경우가 존재한다.
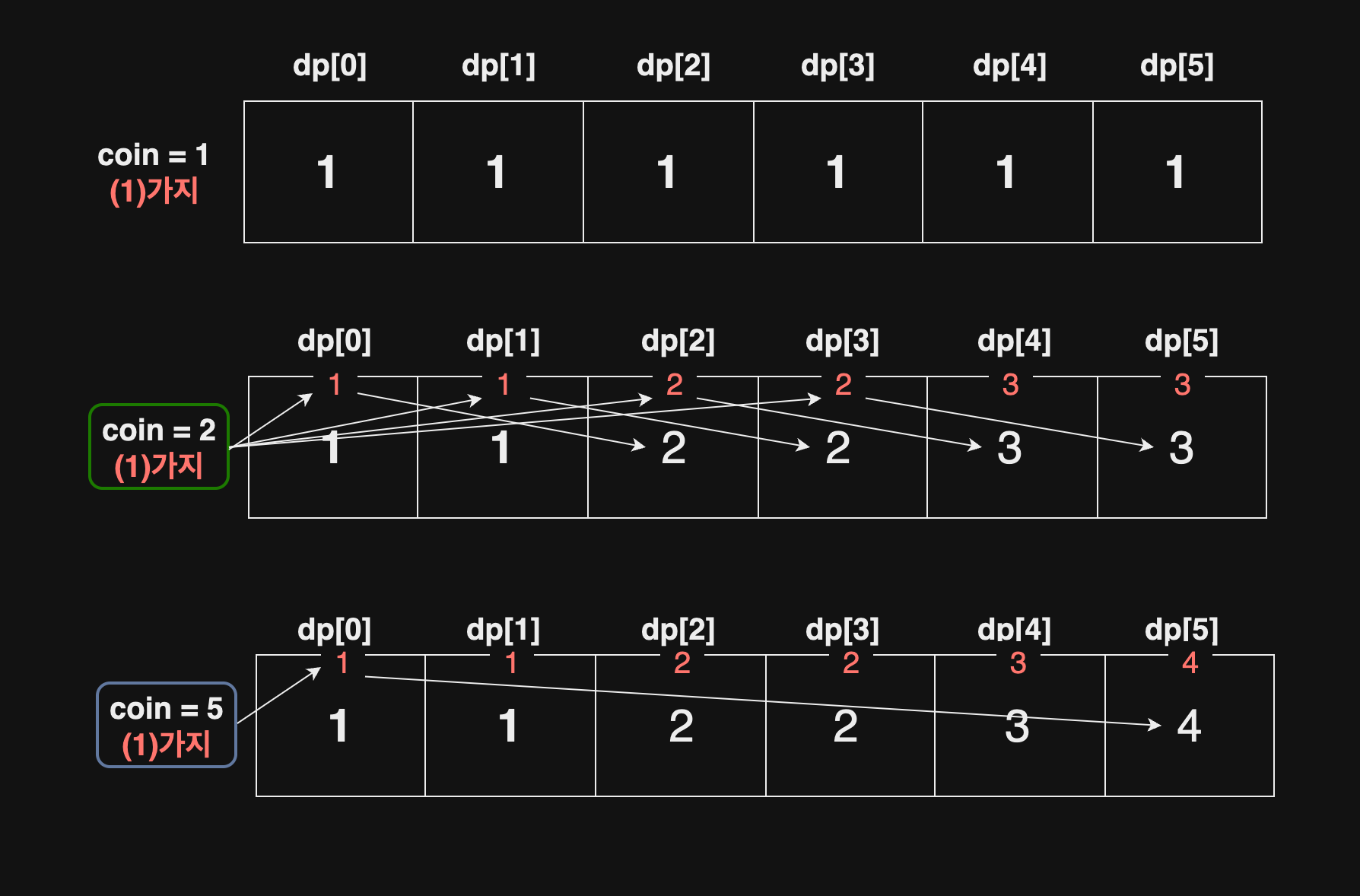
👉🏻 특정 금액을 거슬러 주는 방법의 수를 계산할 때, 더 작은 금액에 대한 문제들이 반복해서 등장한다. 이러한 중복되는 부분 문제들은 DP(Dynamic Programming)를 사용하여 효율적으로 해결 할 수 있다.

- 배열은 각 금액을 만들기 위한 방법의 수를 저장하는 배열로 n + 1 길이로 초기화하는 이유는 0원부터 n원까지 각 금액에 대한 해결책을 저장하기 위함이다.
- dp[0] = 1은 0원을 만드는 방법은 동전을 아무것도 선택하지 않는 한 가지 방법이 있다는 것을 의미한다.



순위
문2) n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
입출력 예
| n | reuslts | return |
|---|---|---|
| 5 | [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5] | 2 |
입출력 예 설명
2번 선수는 [1, 3, 4] 선수에게 패배했고 5번 선수에게 승리했기 때문에 4위입니다.
5번 선수는 4위인 2번 선수에게 패배했기 때문에 5위입니다.
나의 풀이
플로이드 와샬 알고리즘
package programmers;
public class Ranking {
public static int solution(int n, int[][] results) {
boolean[][] graph = new boolean[n+1][n+1];
for(int[] result : results) {
graph[result[0]][result[1]] = true;
}
for(int k = 1; k <= n; k++) {
for(int i = 1; i <=n; i++) {
for(int j = 1; j <= n; j++) {
if(graph[i][k] && graph[k][j]) {
graph[i][j] = true;
}
}
}
}
int answer = 0;
for(int i = 1; i <= n; i++) {
int count = 0;
for(int j = 1; j <= n; j++) {
if(graph[i][j] || graph[j][i]) count++;
}
if(count == n - 1) answer++;
}
return answer;
}
public static void main(String[] args) {
int[][] results = {{4, 3}, {4, 2}, {3, 2}, {1, 2}, {2, 5}};
solution(5, results);
}
}
dfs
package programmers;
public class Ranking {
static boolean[][] graph; // 각 선수 간의 경기 결과를 저장
static boolean[] visited; // DFS 수행 시 방문 여부를 확인하는 배열
static int winCount; // 한 선수가 이긴 횟수
static int loseCount; // 한 선수가 진 횟수
// DFS를 이용하여 한 선수가 이긴 횟수와 진 횟수를 계산하는 함수
public static void dfs(int node, int n, boolean reverse) {
visited[node] = true; // 현재 노드를 방문 처리
for (int i = 1; i <= n; i++) {
// reverse가 true일 경우, 선수가 진 경기를 확인
// reverse가 false일 경우, 선수가 이긴 경기를 확인
if (!visited[i] && (reverse ? graph[i][node] : graph[node][i])) {
if (reverse) {
loseCount++; // 진 경기 수 증가
} else {
winCount++; // 이긴 경기 수 증가
}
dfs(i, n, reverse); // 다음 경기 결과를 확인하기 위해 DFS 재귀 호출
}
}
}
// 주어진 경기 결과를 바탕으로 선수들의 순위를 계산하는 함수
public static int solution(int n, int[][] results) {
graph = new boolean[n+1][n+1]; // 경기 결과를 저장할 그래프 초기화
int answer = 0; // 순위를 확실히 알 수 있는 선수의 수
// 주어진 경기 결과를 바탕으로 선수들의 순위를 계산하는 함수
for(int[] result : results) {
graph[result[0]][result[1]] = true;
}
// 각 선수에 대해 순위를 계산
for(int i = 1; i <= n; i++) {
visited = new boolean[n+1];
winCount = 0;
loseCount = 0;
dfs(i, n, false); // 선수가 이긴 경기 수 계산
visited = new boolean[n+1];
dfs(i, n, true); // 선수가 진 경기 수 계산
// 이긴 경기 수와 진 경기 수의 합이 n-1이면 해당 선수의 순위를 확실히 알 수 있음
if (winCount + loseCount == n - 1) {
answer++;
}
}
System.out.println(answer);
return answer;
}
public static void main(String[] args) {
int[][] results = {{4, 3}, {4, 2}, {3, 2}, {1, 2}, {2, 5}};
solution(5, results);
}
}
나의 생각
처음 문제를 보고 그래프 카테고리에 있어... dfs로 문제를 풀어야겠다고 생각했다. 물론 dfs로 푸는 방법이 존재하긴 하나... dfs로 문제를 풀기가 쉽지않았다. 제일 먼저 든 생각이 모든 반복의 결과로 등수가 확실한 선수를 어떻게 판별할 것인가를 무척 고민하였다. 그러던 와중 플로이드 와샬 알고리즘에 대해서 알게 되었고, 먼저 플로이드 와샬 알고리즘이 뭔지 공부한 뒤 이 문제를 풀어보았다.
👉🏻 플로이드 와샬 알고리즘
먼저 이 문제의 핵심은, 매개변수로 알 수 있는 직접적인 승・패 결과와, 간접적으로 알 수 있는 승・패 결과였다. 해당 문제를 예로들어보면
4 > 3, 4 > 2, 3 > 2, 1 > 2, 2 > 5 (직접적 승・패 결과)
4 > 2 > 5 = 4 > 5 (간접적 승・패 결과)
3 > 2 > 5 = 3 > 5 (간접적 승・패 결과)
1 > 2 > 5 = 1 > 5 (간접적 승・패 결과)
해당 결과를 알 수 있다.
이를 그림으로 나타내면 다음과 같다.
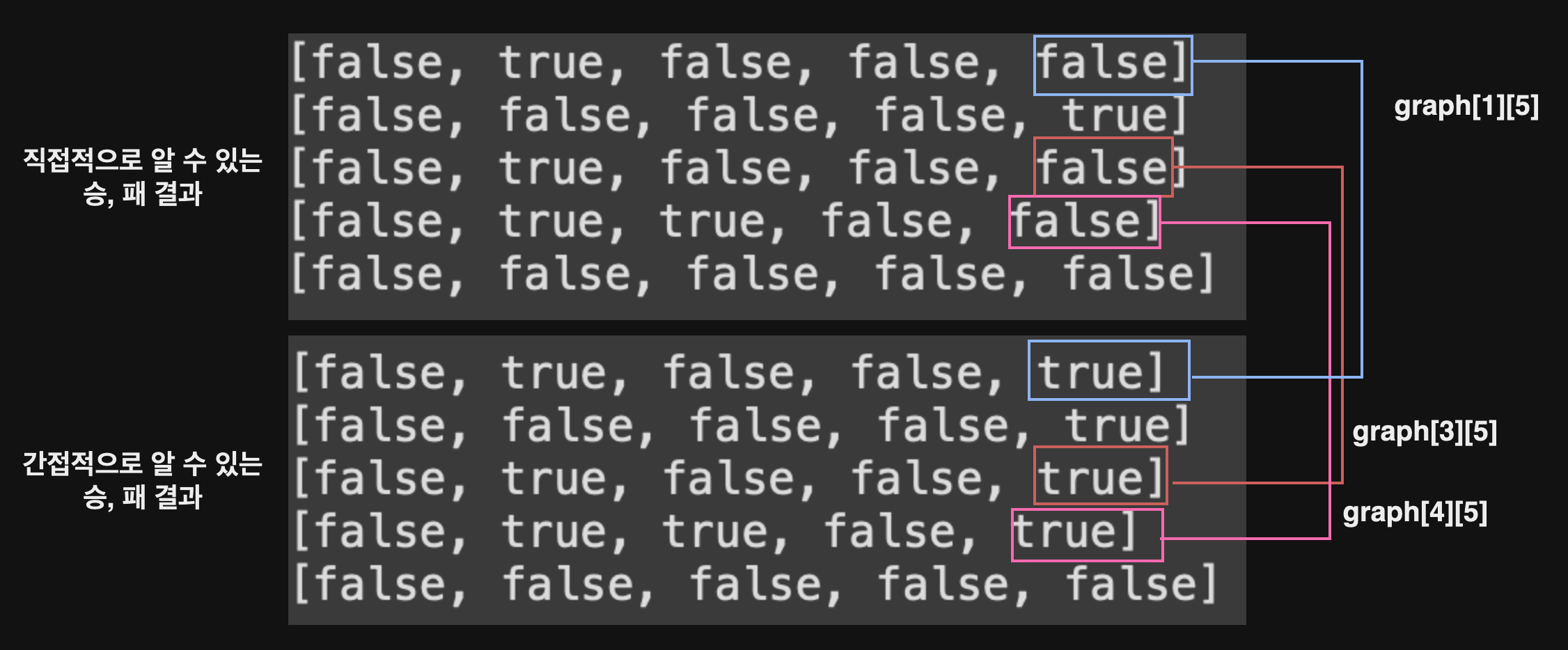
간접적으로 알 수 있는 승・패 결과를 보면 2번 선수는 1,3,4번의 선수에게 지고, 5번 선수에게만 승리하였다. 👉🏻
4위
5번 선수는 모든 선수에게 패배하였다. 👉🏻5위
핵심 로직
int answer = 0;
for(int i = 1; i <= n; i++) {
int count = 0;
for(int j = 1; j <= n; j++) {
if(graph[i][j] || graph[j][i]) count++;
}
if(count == n - 1) answer++;
}2번 선수를 예를들면,
- 2번은 1번에게 패배, 1번은 2번에게 승리 (승 ・ 패가 확실)
- 2번은 3번에게 패배, 3번은 2번애게 승리 (승 ・ 패가 확실)
- 2번은 4번에게 패배, 4번은 2번에게 승리 (승 ・ 패가 확실)
- 2번은 5번에게 승리, 5번은 2번에게 패배 (승 ・ 패가 확실)
👉🏻 즉, 자기 자신을 제외한 나머지 결과가 확실함count == n-1를 만족
플로이드 워샬 알고리즘, dfs 알고리즘 속도차이
| 플로이드 워샬 알고리즘 | dfs 알고리즘 |
|---|---|
 |  |
경주로 건설

문3) 건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.
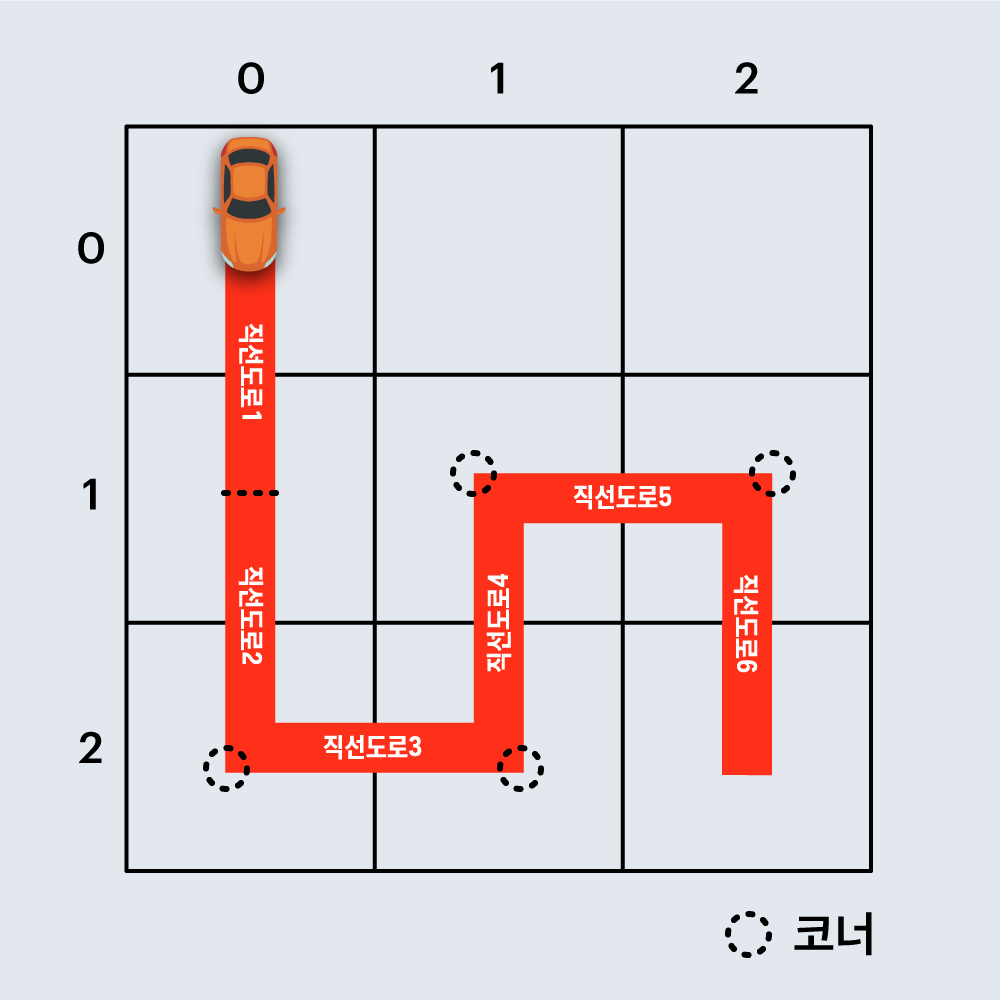
또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.
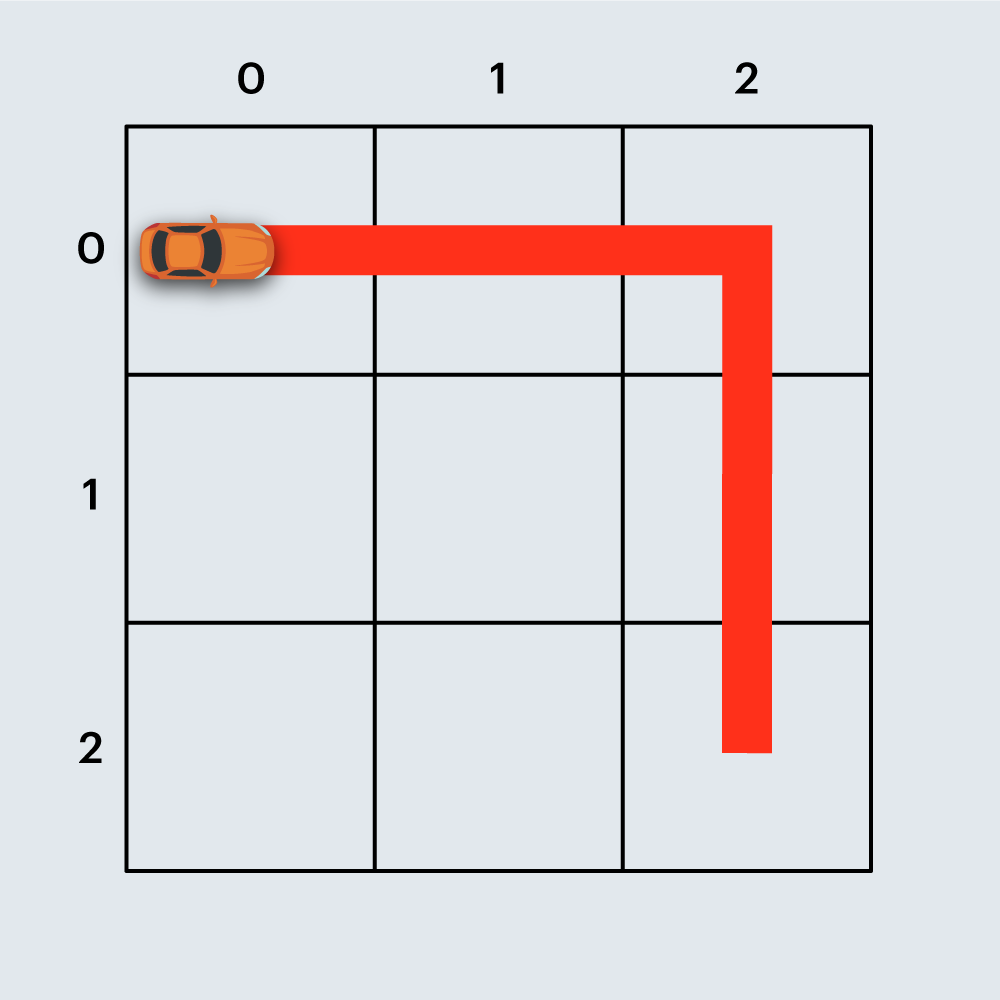
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
제한 사항
- board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
- board 배열의 각 원소의 값은 0 또는 1 입니다.
- 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
- 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
- board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
- 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.
입출력 예
| board | result |
|---|---|
| [[0,0,0],[0,0,0],[0,0,0]] | 900 |
| [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] | 3800 |
| [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] | 2100 |
| [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] | 3200 |
입출력 예 설명
입출력 예 #2
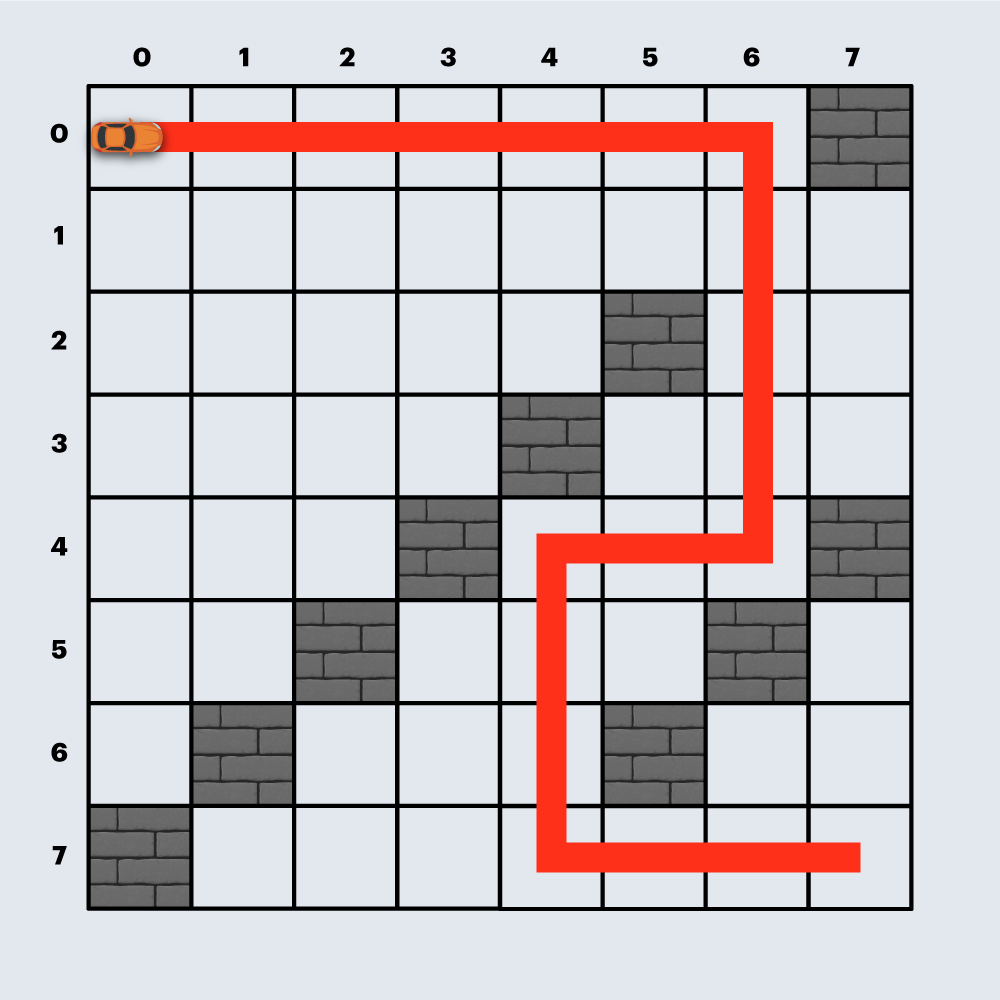
- 위와 같이 경주로를 건설하면 직선 도로 18개, 코너 4개로 총 3800원이 듭니다.
입출력 예 #3
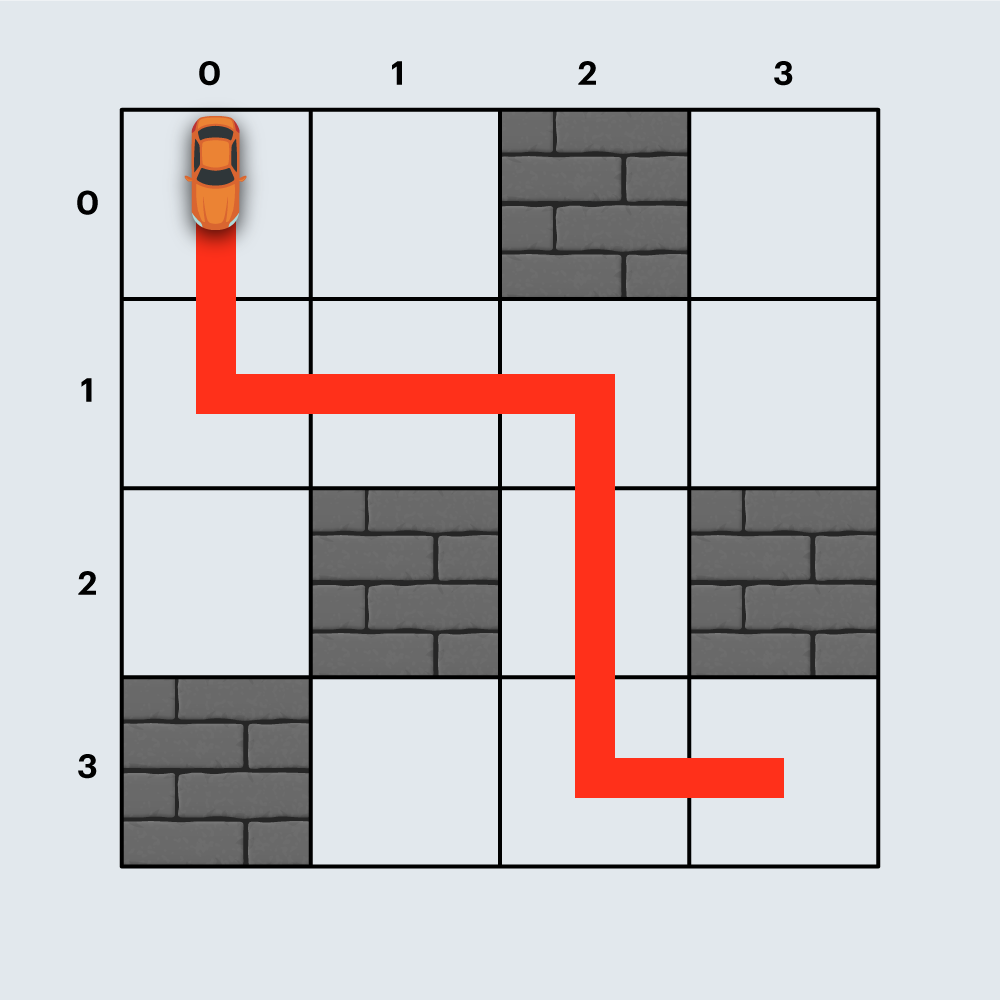
- 위와 같이 경주로를 건설하면 직선 도로 6개, 코너 3개로 총 2100원이 듭니다.
입출력 예 #4
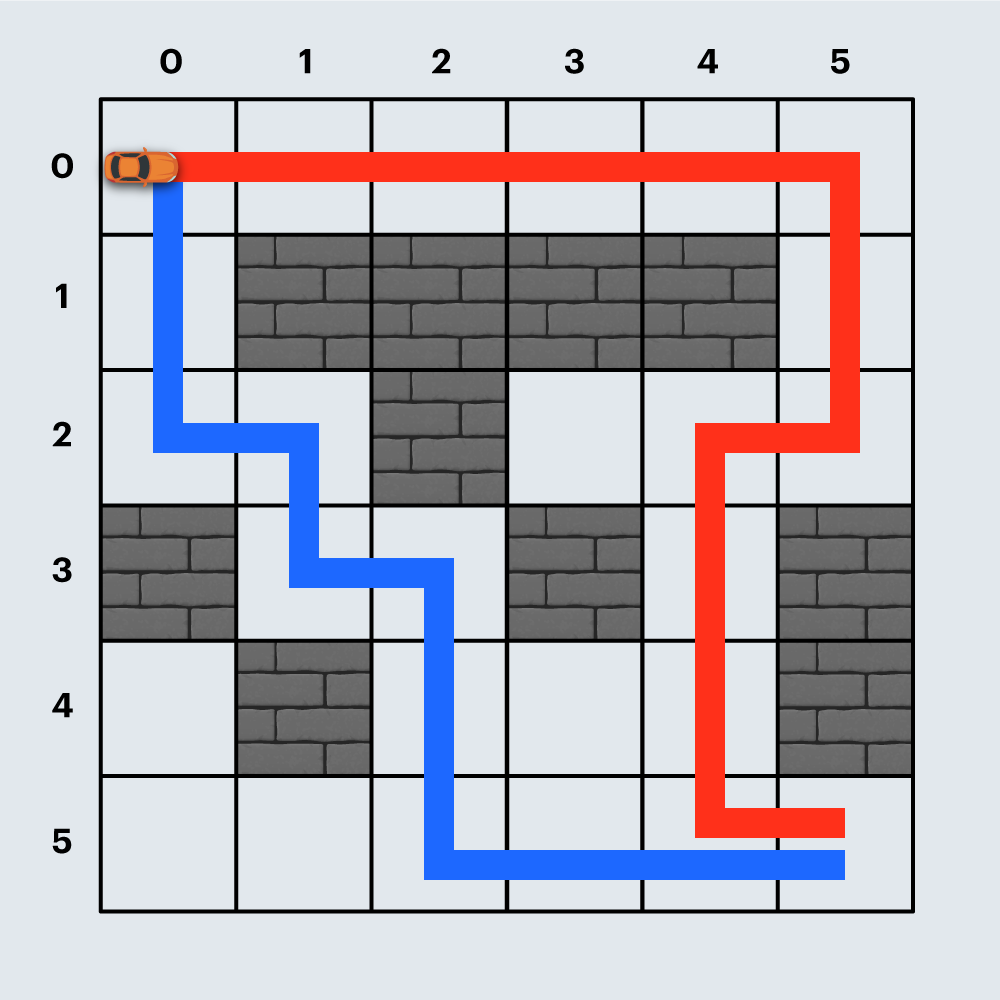
- 붉은색 경로와 같이 경주로를 건설하면 직선 도로 12개, 코너 4개로 총 3200원이 듭니다.
만약, 파란색 경로와 같이 경주로를 건설한다면 직선 도로 10개, 코너 5개로 총 3500원이 들며, 더 많은 비용이 듭니다.
나의 풀이
DFS로 접근한 풀이
package programmers;
import java.util.Arrays;
public class RaceRoadConstruction {
static int[][] DIRS = {{-1,0},{1,0},{0,-1},{0,1}};
static int[][][] cost;
static int N;
static final int STRAIGHT_COST = 100;
static final int CORNER_COST = 500;
public static void dfs(int[][] board, int y, int x, int prevDir, int accCost) {
if (y == N - 1 && x == N - 1) {
cost[y][x][prevDir] = Math.min(cost[y][x][prevDir], accCost);
return;
}
for (int i = 0; i < 4; i++) {
int newY = y + DIRS[i][0];
int newX = x + DIRS[i][1];
if (newY >= 0 && newY < N && newX >= 0 && newX < N && board[newY][newX] == 0) {
int newCost = accCost + STRAIGHT_COST;
if (prevDir != -1 && prevDir != i) {
newCost += CORNER_COST;
}
if (newCost < cost[newY][newX][i]) {
cost[newY][newX][i] = newCost;
dfs(board, newY, newX, i, newCost);
}
}
}
}
public static int solution(int[][] board) {
N = board.length;
cost = new int[N][N][4];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
Arrays.fill(cost[i][j], Integer.MAX_VALUE);
}
}
for (int i = 0; i < 4; i++) {
cost[0][0][i] = 0;
}
dfs(board, 0, 0, -1, 0);
int minCost = Integer.MAX_VALUE;
for (int i = 0; i < 4; i++) {
if (cost[N-1][N-1][i] < minCost) {
minCost = cost[N-1][N-1][i];
}
}
return minCost;
}
public static void main(String[] args) {
int[][] board = {{0,0,0},{0,0,0},{0,0,0}};
}
}
BFS로 접근한 풀이
package programmers;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class RaceRoadConstruction {
static int[][] DIRS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
static int[][][] cost;
static int N;
static final int STRAIGHT = 100;
static final int CORNER = 500;
public static void bfs(int[][] board) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{0, 0, -1, 0});
while (!queue.isEmpty()) {
int[] current = queue.poll();
int y = current[0];
int x = current[1];
int prevDir = current[2];
int accCost = current[3];
for (int i = 0; i < 4; i++) {
int newY = y + DIRS[i][0];
int newX = x + DIRS[i][1];
if (newY >= 0 && newY < N && newX >= 0 && newX < N && board[newY][newX] == 0) {
int newCost = accCost + STRAIGHT;
if (prevDir != -1 && prevDir != i) {
newCost += CORNER;
}
if (newCost < cost[newY][newX][i]) {
cost[newY][newX][i] = newCost;
queue.offer(new int[]{newY, newX, i, newCost});
}
}
}
}
}
public static int solution(int[][] board) {
N = board.length;
cost = new int[N][N][4];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
Arrays.fill(cost[i][j], Integer.MAX_VALUE);
}
}
for (int i = 0; i < 4; i++) {
cost[0][0][i] = 0;
}
bfs(board);
int minCost = Integer.MAX_VALUE;
for (int i = 0; i < 4; i++) {
if (cost[N-1][N-1][i] < minCost) {
minCost = cost[N-1][N-1][i];
}
}
return minCost;
}
public static void main(String[] args) {
int[][] board = {{0,0,0},{0,0,0},{0,0,0}};
solution(board);
}
}
나의 생각
시작점에서 도착지점까지 가는데 설치하는 경주로의 최소 비용을 리턴하는 문제임을 파악하자마자 BFS로 문제를 풀어야겠다는 생각이 들었다. 하지만 큰 틀을 잡는 부분에서 헤매다가 DFS로 먼저 접근을 해보았다.
- 클래스 변수 설정
static int[][] DIRS = {{-1,0},{1,0},{0,-1},{0,1}}; // 이동 가능한 방향(상, 하, 좌, 우)을 나타내는 2차원 배열
static int[][][] cost; // 각 위치까지 이동하는 데 드는 비용을 저장할 3차원 배열
static int N; // 보드의 크기(N x N)를 저장할 변수
static final int STRAIGHT_COST = 100; // 직선 도로 건설 비용
static final int CORNER_COST = 500; // 코너 도로 건설 비용 - 주요 메서드
public static int solution(int[][] board) {
N = board.length; // 보드 크기를 N으로 초기화
cost = new int[N][N][4]; // 비용 배열을 N * N * 4 크기로 초기화
// 모든 비용을 최댓값으로 초기화
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
Arrays.fill(cost[i][j], Integer.MAX_VALUE);
}
}
// 시작 위치의 비용을 0으로 초기화
for (int i = 0; i < 4; i++) {
cost[0][0][i] = 0;
}
// DFS 시작
dfs(board, 0, 0, -1, 0);
// BFS 시작
bfs(board);
// 도착지점까지의 최소 비용을 계산
int minCost = Integer.MAX_VALUE;
for (int i = 0; i < 4; i++) {
if (cost[N-1][N-1][i] < minCost) {
minCost = cost[N-1][N-1][i];
}
}
return minCost;
}public static void dfs(int[][] board, int y, int x, int prevDir, int accCost) {
if (y == N - 1 && x == N - 1) { // 목적지에 도착했을 경우 최소 비용을 리턴
cost[y][x][prevDir] = Math.min(cost[y][x][prevDir], accCost);
return;
}
for (int i = 0; i < 4; i++) { // 모든 방향에 대해서 탐색
int newY = y + DIRS[i][0]; // 다음 y 좌표 계산
int newX = x + DIRS[i][1]; // 다음 x 좌표 계산
// 보드 범위 안에 있고, 벽이 아닌 경우에만 진행
if (newY >= 0 && newY < N && newX >= 0 && newX < N && board[newY][newX] == 0) {
int newCost = accCost + STRAIGHT_COST; // 직선 도로 비용을 추가
// 이전 방향과 다른 경우 코너 비용 추가
if (prevDir != -1 && prevDir != i) {
newCost += CORNER_COST;
}
// 새로운 비용이 기존 비용보다 적을 때만 진행
if (newCost < cost[newY][newX][i]) {
cost[newY][newX][i] = newCost; // 비용 업데이트
dfs(board, newY, newX, i, newCost); // 새 위치에서 다시 DFS 수행
}
}
}
}public static void bfs(int[][] board) { // 너비 우선 탐색(BFS) 알고리즘을 구현한 메서드
Queue<int[]> queue = new LinkedList<>(); // BFS를 위한 큐 생성
queue.offer(new int[]{0, 0, -1, 0}); // 시작 지점과 초기 비용을 큐에 추가
while (!queue.isEmpty()) { // 큐가 비어있지 않는 동안 반복
int[] current = queue.poll(); // 큐에서 현재 위치와 비용 정보를 가져옴
int y = current[0]; // 현재 y 좌표
int x = current[1]; // 현재 x 좌표
int prevDir = current[2]; // 이전에 이동한 방향
int accCost = current[3]; // 현재까지 누적된 비용
for (int i = 0; i < 4; i++) { // 모든 방향에 대해 탐색
int newY = y + dirs[i][0]; // 다음 y 좌표 계산
int newX = x + dirs[i][1]; // 다음 x 좌표 계산
// 다음 좌표가 범위 내에 있고 벽이 아닌 경우
if (newY >= 0 && newY < N && newX >= 0 && newX < N && board[newY][newX] == 0) {
int newCost = accCost + STRAIGHT; // 직선 비용을 더함
// 이전 방향과 다른 경우 코너 비용 추가
if (prevDir != -1 && prevDir != i) {
newCost += CORNER;
}
// 새 비용이 기존 비용보다 적을 경우 업데이트
if (newCost < cost[newY][newX][i]) {
cost[newY][newX][i] = newCost; // 비용을 업데이트
queue.offer(new int[]{newY, newX, i, newCost}); // 큐에 새 위치와 비용 정보 추가
}
}
}
}
}| 측면 | BFS 메서드 | DFS 메서드 |
|---|---|---|
| 주요 메서드 | 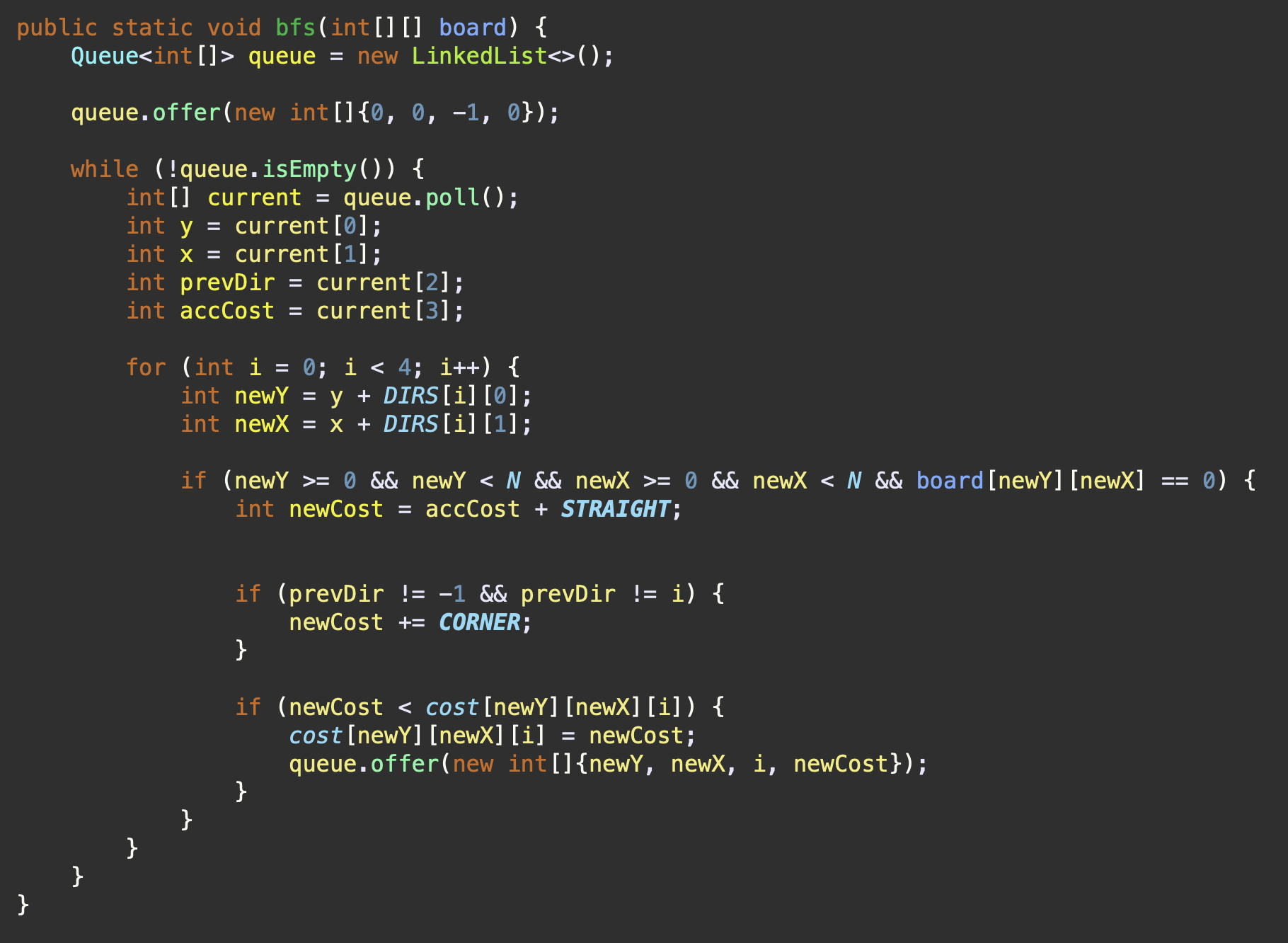 | 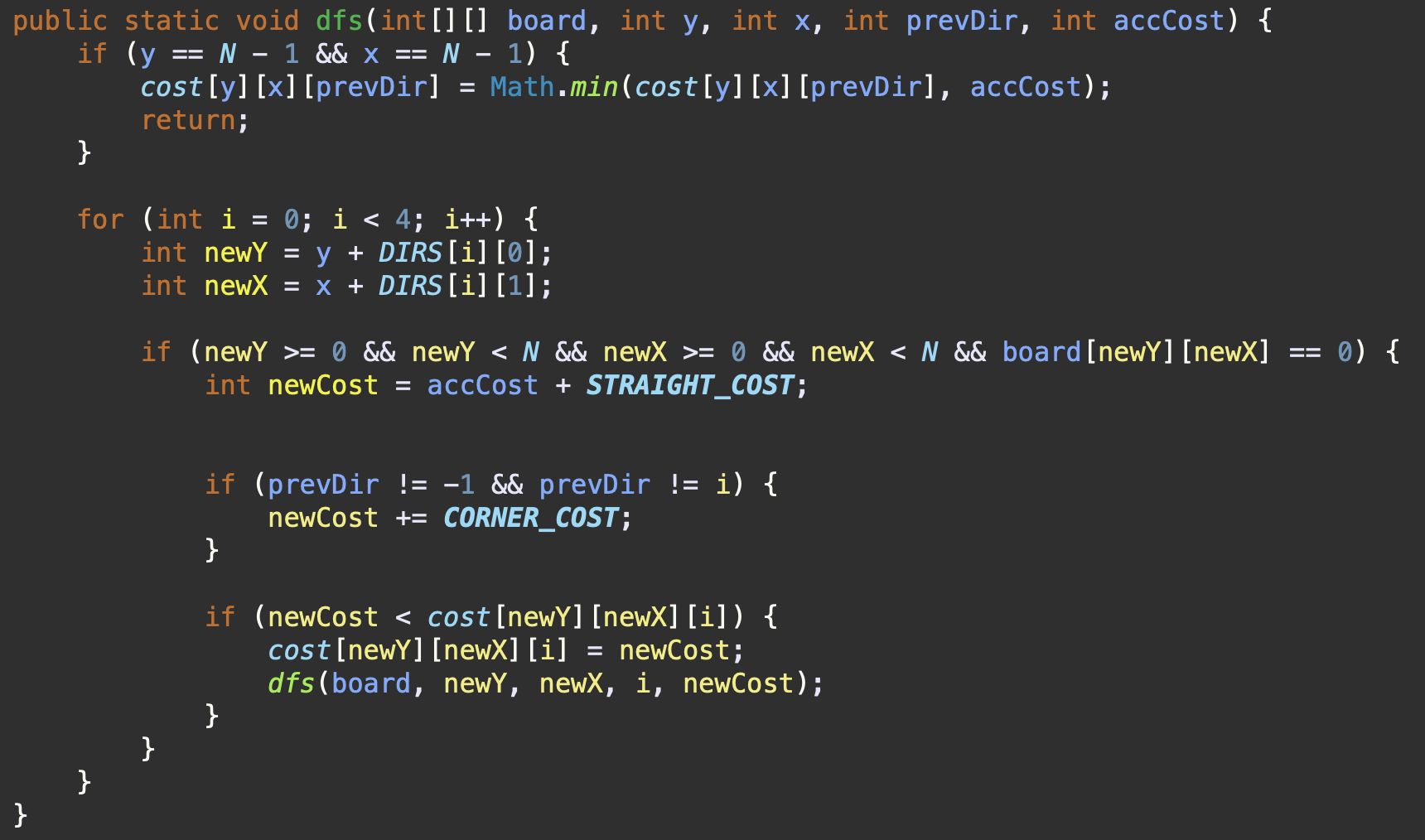 |
| 측면 | BFS 메서드 | DFS 메서드 |
|---|---|---|
| 검색 전략 | 너비 우선 탐색 | 깊이 우선 탐색 |
| 데이터 구조 | 큐 | 스택 (재귀를 통해 암시적으로 사용) |
| 초기화 | 시작점 (0,0)으로 큐 초기화 | 시작점 (0,0)으로 재귀 호출 시작 |
| 루프 메커니즘 | 큐가 비어있지 않는 동안 반복 | 기저 조건이 만족될 때까지 재귀 |
| 경로 확장 | 가능한 모든 다음 이동을 큐에 추가 | 가능한 각 다음 이동에 대해 재귀 호출 |
| 비용 계산 | STRAIGHT 비용 추가, 방향 변경 시 CORNER 비용 추가 | STRAIGHT_COST 추가, 방향 변경 시 CORNER_COST 추가 |
| 비용 비교 | 새 비용이 현재 위치의 비용보다 낮으면 비용 업데이트 후 큐에 추가 | 새 비용이 현재 위치의 비용보다 낮으면 비용 업데이트 후 해당 위치로 재귀 |
| 종료 조건 | 큐가 비어 있음 | 기저 조건 만족 (대개 목표 도달 시 또는 더 이상 이동 가능하지 않을 때) |
| 방향 변경 | 방향 변경 확인 후 CORNER 비용 추가 | 방향 변경 확인 후 CORNER_COST 추가 |
| 최적성 | 존재하는 경우 항상 최단 경로를 찾음 | 비가중 그래프에서는 최단 경로를 보장하지 않음 |
| 효율성 | 현재 너비 레벨의 모든 노드를 저장하기 때문에 메모리 사용 면에서 비효율적일 수 있음 | 현재 노드까지의 경로만 저장하기 때문에 메모리 사용 면에서 더 효율적임 |
| 복잡도 | O(V+E) 여기서 V는 정점의 수, E는 간선의 수 | O(V+E)지만 최악의 경우에 덜 효율적일 수 있음 |
| 사용 상황 | 최단 경로가 필요할 때 사용됨 | 목표까지의 경로가 있으면 되는 경우나 가능한 모든 경로를 탐색할 때 사용됨 |
| dfs 속도 | bfs 속도 |
|---|---|
 | 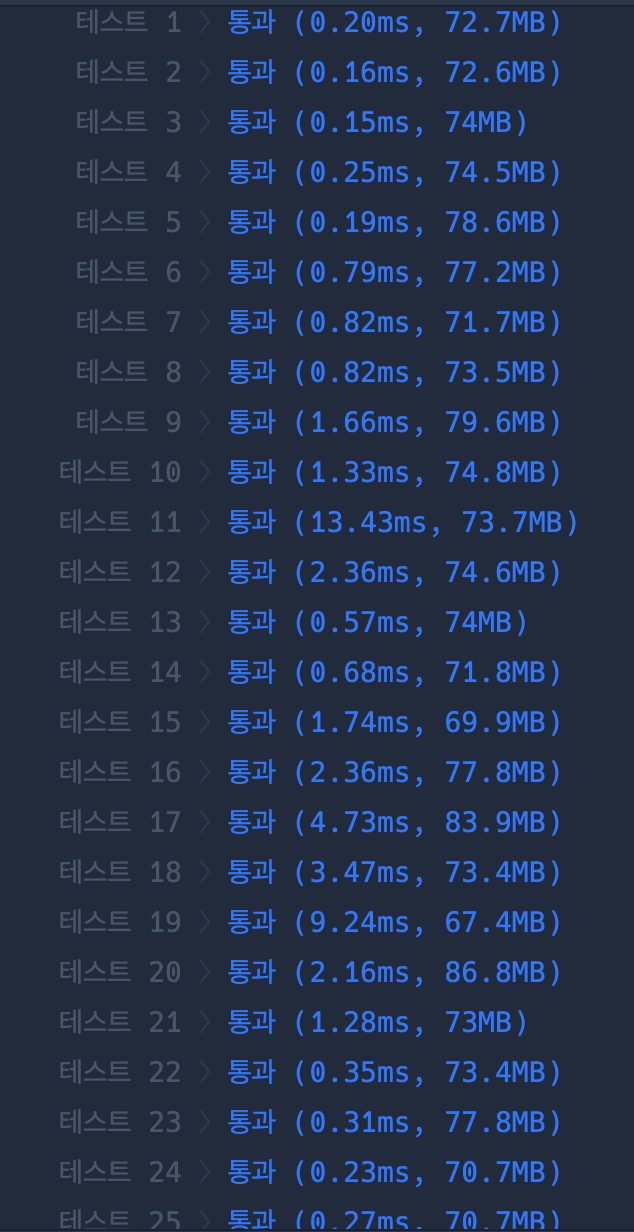 |
셔틀버스
문4) 카카오에서는 무료 셔틀버스를 운행하기 때문에 판교역에서 편하게 사무실로 올 수 있다. 카카오의 직원은 서로를 '크루'라고 부르는데, 아침마다 많은 크루들이 이 셔틀을 이용하여 출근한다. 이 문제에서는 편의를 위해 셔틀은 다음과 같은 규칙으로 운행한다고 가정하자.
- 셔틀은 09:00부터 총 n회 t분 간격으로 역에 도착하며, 하나의 셔틀에는 최대 m명의 승객이 탈 수 있다.
- 셔틀은 도착했을 때 도착한 순간에 대기열에 선 크루까지 포함해서 대기 순서대로 태우고 바로 출발한다. 예를 들어 09:00에 도착한 셔틀은 자리가 있다면 09:00에 줄을 선 크루도 탈 수 있다.
일찍 나와서 셔틀을 기다리는 것이 귀찮았던 콘은, 일주일간의 집요한 관찰 끝에 어떤 크루가 몇 시에 셔틀 대기열에 도착하는지 알아냈다. 콘이 셔틀을 타고 사무실로 갈 수 있는 도착 시각 중 제일 늦은 시각을 구하여라.
단, 콘은 게으르기 때문에 같은 시각에 도착한 크루 중 대기열에서 제일 뒤에 선다. 또한, 모든 크루는 잠을 자야 하므로 23:59에 집에 돌아간다. 따라서 어떤 크루도 다음날 셔틀을 타는 일은 없다.
입력 형식
셔틀 운행 횟수 n, 셔틀 운행 간격 t, 한 셔틀에 탈 수 있는 최대 크루 수 m, 크루가 대기열에 도착하는 시각을 모은 배열 timetable이 입력으로 주어진다.
- 0 < n ≦ 10
- 0 < t ≦ 60
- 0 < m ≦ 45
timetable은 최소 길이 1이고 최대 길이 2000인 배열로, 하루 동안 크루가 대기열에 도착하는 시각이HH:MM형식으로 이루어져 있다.- 크루의 도착 시각
HH:MM은00:01에서23:59사이이다.
출력 형식
콘이 무사히 셔틀을 타고 사무실로 갈 수 있는 제일 늦은 도착 시각을 출력한다. 도착 시각은 HH:MM 형식이며, 00:00에서 23:59 사이의 값이 될 수 있다.
입출력 예제
| n | t | m | timetable | answer |
|---|---|---|---|---|
| 1 | 1 | 5 | ["08:00", "08:01", "08:02", "08:03"] | "09:00" |
| 2 | 10 | 2 | ["09:10", "09:09", "08:00"] | "09:09" |
| 2 | 1 | 2 | ["09:00", "09:00", "09:00", "09:00"] | "08:59" |
| 1 | 1 | 5 | ["00:01", "00:01", "00:01", "00:01", "00:01"] " | "00:00" |
| 1 | 1 | 1 | ["23:59"] | "09:00" |
| 10 | 60 | 45 | ["23:59","23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59", "23:59"] | "18:00" |
나의 풀이
처음 구현한 로직
package programmers;
import java.time.LocalTime;
import java.time.format.DateTimeFormatter;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class ShuttleBus {
static LocalTime[] busOperatingTimeList ;
static class Bus{
int n;
int t;
int m;
public Bus(int n, int t, int m) {
this.n = n;
this.t = t;
this.m = m;
}
public void getTime() {
busOperatingTimeList = new LocalTime[n];
LocalTime startTime = LocalTime.of(9, 0);
for(int i = 0; i < n; i++) {
busOperatingTimeList[i] = startTime;
startTime = startTime.plusMinutes(t);
}
}
}
public static String solution(int n, int t, int m, String[] timetable) {
List<LocalTime> crewList = new ArrayList<>();
DateTimeFormatter formatter = DateTimeFormatter.ofPattern("HH:mm");
Bus bus = new Bus(n, t, m);
bus.getTime();
for(String time : timetable) {
LocalTime crewTime = LocalTime.parse(time, formatter);
if (!crewTime.equals(LocalTime.of(23, 59))) {
crewList.add(crewTime);
}
}
Collections.sort(crewList);
LocalTime answer = LocalTime.of(9, 0);
int crewIndex = 0;
for(int i = 0; i < n; i++) {
int thisBusCapacity = m;
LocalTime lastCrewTime = null;
while (crewIndex < crewList.size() && thisBusCapacity > 0 && crewList.get(crewIndex).compareTo(busOperatingTimeList[i]) <= 0) {
lastCrewTime = crewList.get(crewIndex);
crewIndex++;
thisBusCapacity--;
}
if (i == n - 1) {
if (thisBusCapacity > 0) {
answer = busOperatingTimeList[i];
} else {
answer = lastCrewTime.minusMinutes(1);
}
}
}
return answer.format(formatter);
}
public static void main(String[] args) {
String[] timetable = {"09:10", "09:09", "08:00"};
solution(2, 10, 2, timetable);
}
}
최적화 로직
package programmers;
import java.time.LocalTime;
import java.time.format.DateTimeFormatter;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class ShuttleBus {
public static String solution(int n, int t, int m, String[] timetable) {
List<LocalTime> crewTimes = new ArrayList<>();
DateTimeFormatter formatter = DateTimeFormatter.ofPattern("HH:mm");
LocalTime maxTime = LocalTime.of(23, 59);
for (String time : timetable) {
LocalTime crewTime = LocalTime.parse(time, formatter);
if (!crewTime.equals(maxTime)) {
crewTimes.add(crewTime);
}
}
Collections.sort(crewTimes);
LocalTime busTime = LocalTime.of(9, 0);
int lastBusTime = 0;
int crewIndex = 0;
for(int i = 0; i < n; i++) {
int capacity = m;
while (capacity > 0 && crewIndex < crewTimes.size() && crewTimes.get(crewIndex).compareTo(busTime) <= 0) {
lastBusTime = crewIndex;
crewIndex++;
capacity--;
}
if (i == n - 1) {
if (capacity > 0) {
return busTime.format(formatter);
} else {
return crewTimes.get(lastBusTime).minusMinutes(1).format(formatter);
}
}
busTime = busTime.plusMinutes(t);
}
return "";
}
public static void main(String[] args) {
String[] timetable = {"09:10", "09:09", "08:00"};
solution(2, 10, 2, timetable);
}
}
나의 생각
위 문제는 크루들의 도착 시간을 관리하고, 각 셔틀버스가 도착하는 시간 을 계산한 다음, 각 셔틀버스 별로 크루들을 태우는 과정에서 크루의 탑승 시간 및 콘이 탑승할 수 있는 마지막 시간을 계산하는게 주요 포인트였던것 같다.
최적화 이후의 로직을 세부적으로 나누어서 설명하겠다.
- 크루원들의 탑승시간(문자열)을 시간 객체로 파싱하기
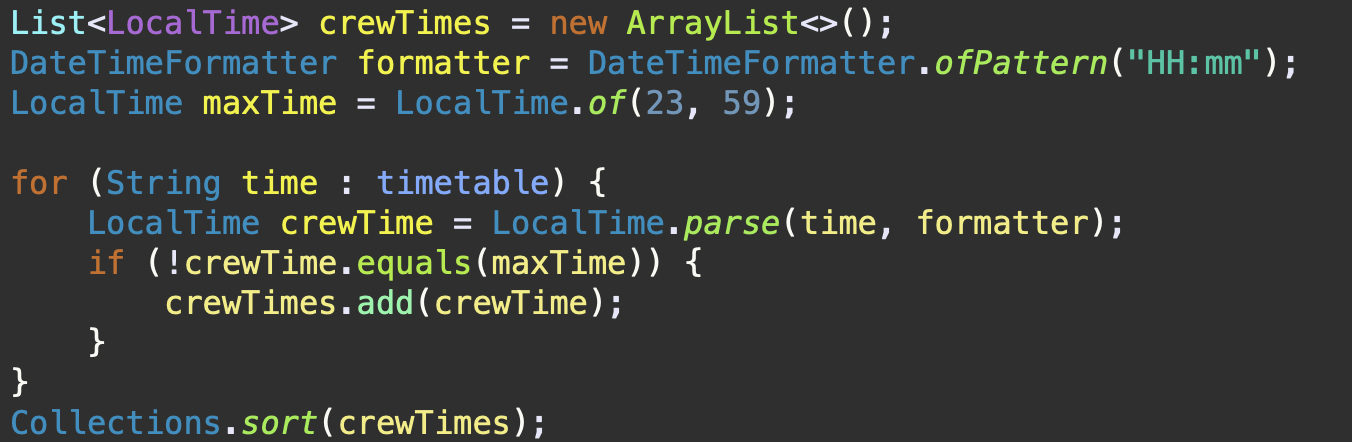
매개변수로 주어진
timetable을 가공없이 사용하면 좋겠지만,23:59과 같이 계산할 필요가 없는 값이나, 크루들의 도착시간을 오름차순으로 정렬하기위해 이 시간을 리스트로 관리

해당 포맷은 시간을 "HH:mm" 패턴으로 저장하겠다는 의미로 0~23시까지를 나타낼 때에는 HH, 0~12시 까지를 나타낼 때에는
hh:mm을 사용

해당 로직은 timetable의 문자열을 시간 객체로 파싱하여 저장하고, 그 시간이
23:59인지를 먼저 확인하여23:59이 아니면crewTime리스트에 저장하고, 최종적으로 오름차순 정렬을 하여 리스트를 나타낸다. 위 과정으로 timetable에 있는 모든 문자열이 시간객체로 변환되어 crewTime 리스트에 저장(오름차순) 된다.


- crewTime 리스트의 값을 바탕으로 콘이 마지막으로 타야할 셔틀버스의 시간을 검출하는 로직
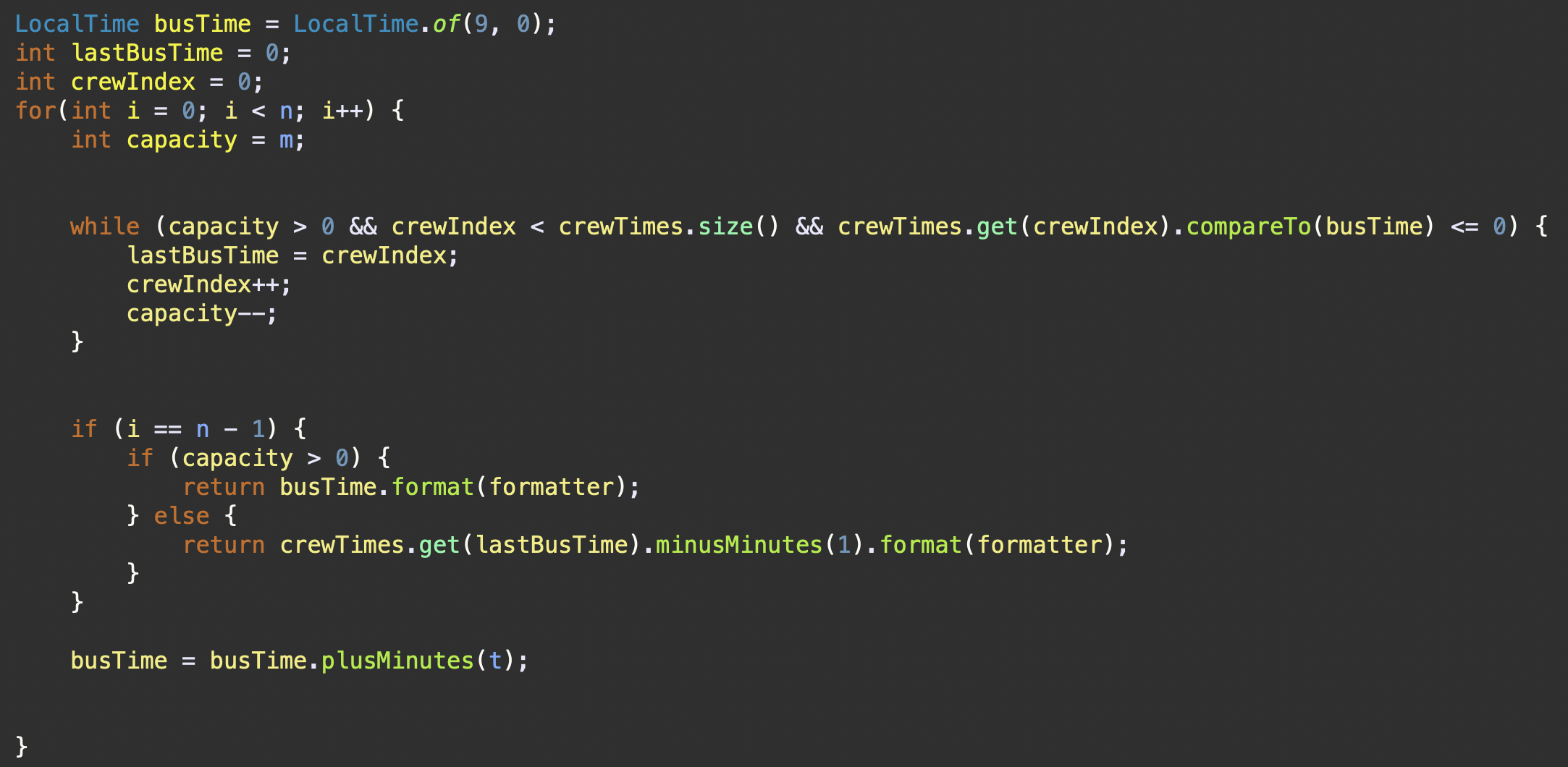
첫 번째 셔틀버스의 도착 시간(
busTime)은09:00으로 고정
lastBusTime = 0, crewIndex = 0으로 초기화 및 반복문 실행
반복은 n 크기만큼 수행
capacity는 각 각의 버스가 수용할 수 있는 인원을 의미 (m = 2명이면, 한 버스당 2명의 인원을 태울 수 있음)
핵심 로직
while (capacity > 0 && crewIndex < crewTimes.size() &&
crewTimes.get(crewIndex).compareTo(busTime) <= 0) {
lastBusTime = crewIndex;
crewIndex++;
capacity--;
}위 로직의 세 조건이 모두 참일 경우 루프의 내용이 실행되는데,
capacity > 0셔틀 버스에 아직 자리가 남아 있는지
crewIndex < crewTime.size()처리할 크루가 더 남았는지
crewTimes.get(crewIndex).compareTo(busTime) <= 0현재 처리 중인 크루의 도착 시간이 셔틀버스 도착 시간 이전이거나 같은지 모든 조건을 확인한다.
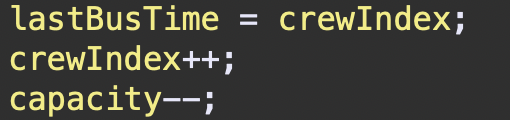
현재 셔틀버스의 출발 시간 전에 도착한 크루를 탑승시키고, 버스의 탑승 인원을 관리하는 것

마지막 셔틀버스를 처리하는 로직
만약 마지막 버스에 자리가 남아있다면(capacity > 0), 콘은 그 버스의 출발 시간에 맞춰 도착할 수 있음
만약 마지막 버스가 꽉 찼다면(capacity == 0), 콘은 마지막으로 탑승한 크루가 도착한 시간보다 1분 먼저 도착해야 함

셔틀버스의 다음 출발 시간을 계산하기 위해 현재 버스 시간에
t분을 더함
| 최적화 전 | 최적화 이후 |
|---|---|
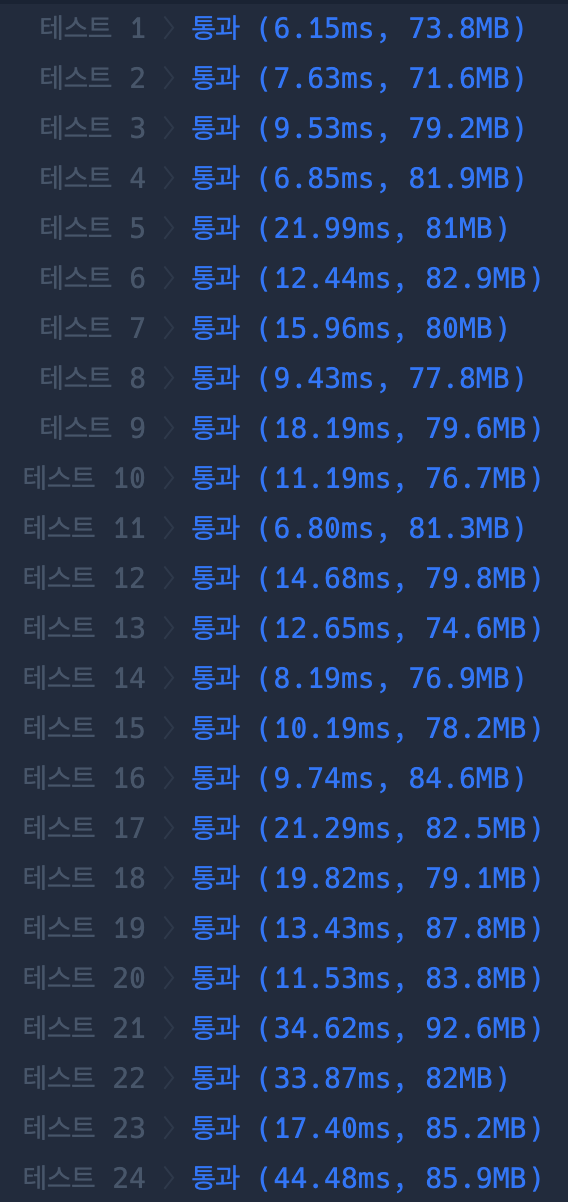 | 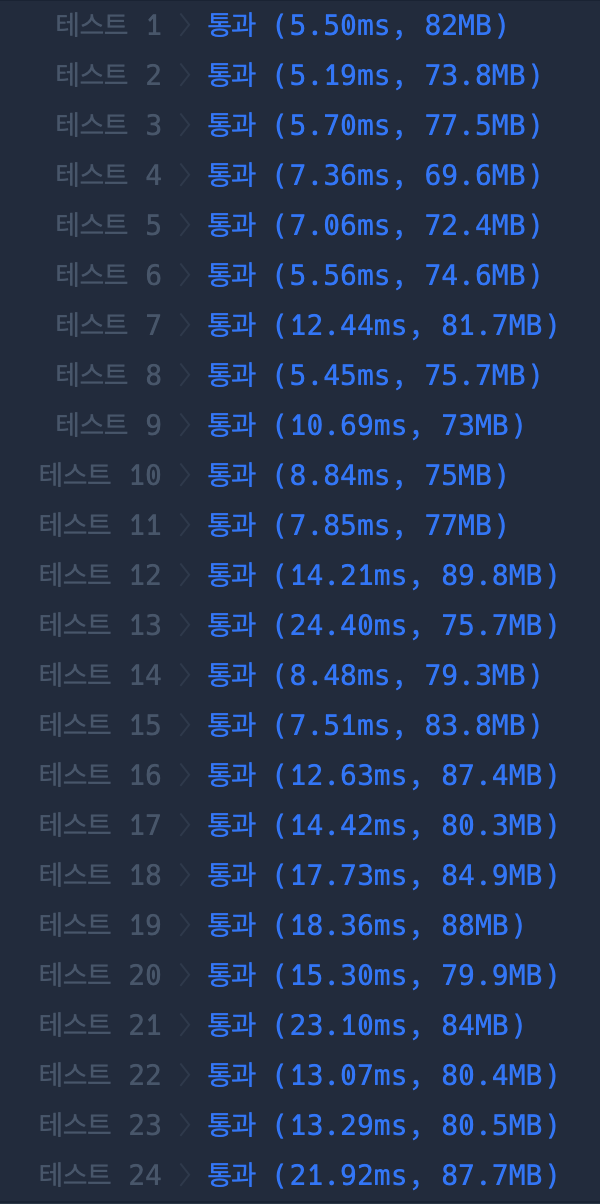 |
합승 택시 요금
문5) 밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.
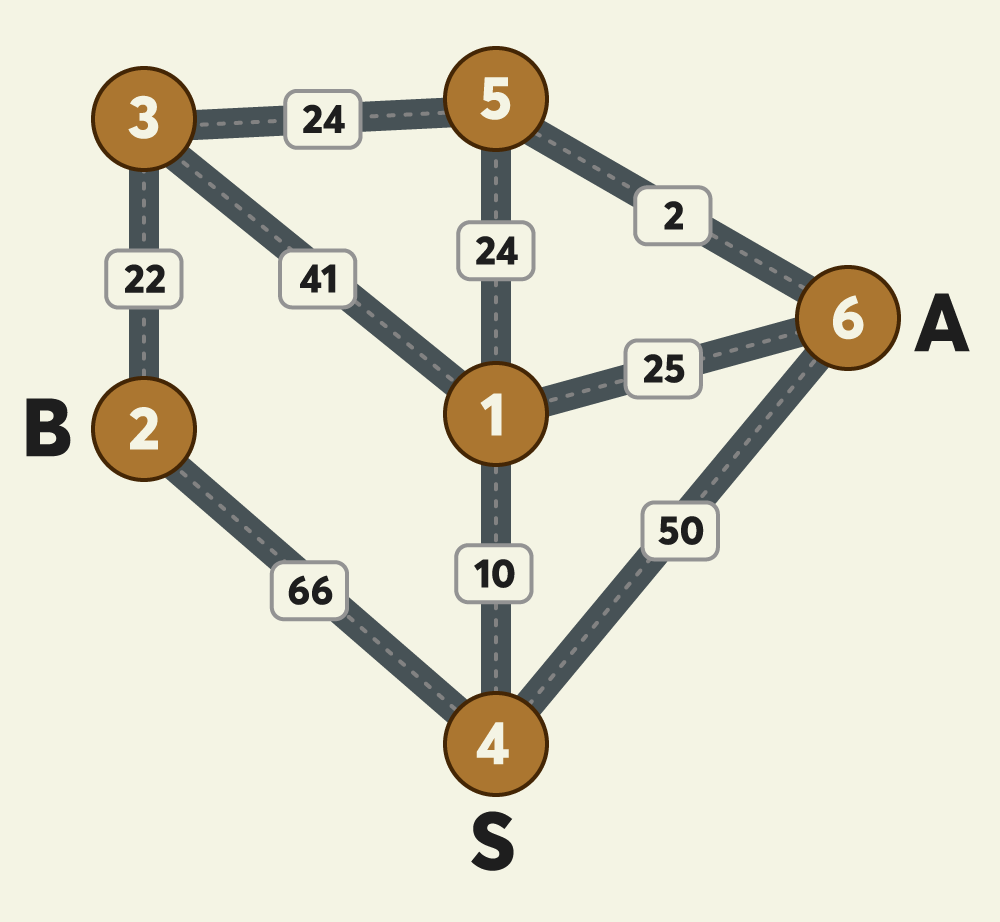
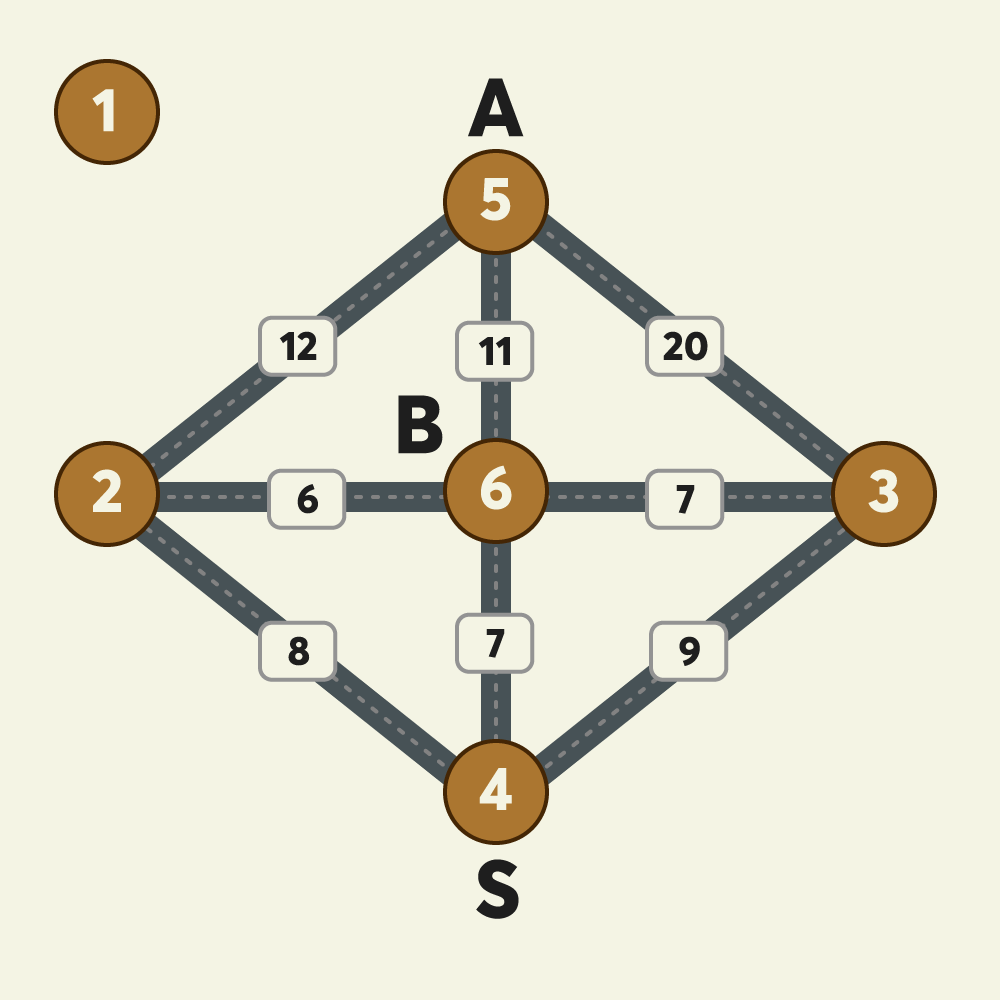
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시노선과 예상요금을 보여주고 있습니다.
그림에서 A와 B 두 사람은 출발지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.
- 그림의 원은 지점을 나타내며 원 안의 숫자는 지점 번호를 나타냅니다.
- 지점이 n개일 때, 지점 번호는 1부터 n까지 사용됩니다.
- 지점 간에 택시가 이동할 수 있는 경로를 간선이라 하며, 간선에 표시된 숫자는 두 지점 사이의 예상 택시요금을 나타냅니다.
- 간선은 편의 상 직선으로 표시되어 있습니다.
- 위 그림 예시에서, 4번 지점에서 1번 지점으로(4→1) 가거나, 1번 지점에서 4번 지점으로(1→4) 갈 때 예상 택시요금은 10원으로 동일하며 이동 방향에 따라 달라지지 않습니다.
- 예상되는 최저 택시요금은 다음과 같이 계산됩니다.
- 4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원 입니다.
- 5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원 입니다.
- 5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원 입니다.
- A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원 입니다.
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.
제한사항
- 지점갯수 n은 3 이상 200 이하인 자연수입니다.
- 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 즉, 출발지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다.
- fares는 2차원 정수 배열입니다.
- fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.
- 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15)
- fares 배열의 각 행은 [c, d, f] 형태입니다.
- c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다. - 요금 f는 1 이상 100,000 이하인 자연수입니다.
- fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.
- 출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
입출력 예
| n | s | a | b | fares | result |
|---|---|---|---|---|---|
| 6 | 4 | 6 | 2 | [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]] | 82 |
| 7 | 3 | 4 | 1 | [[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]] | 14 |
| 6 | 4 | 5 | 6 | [[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4,8], [4,3,9]] | 18 |
입출력 예 설명
입출력 예 #2
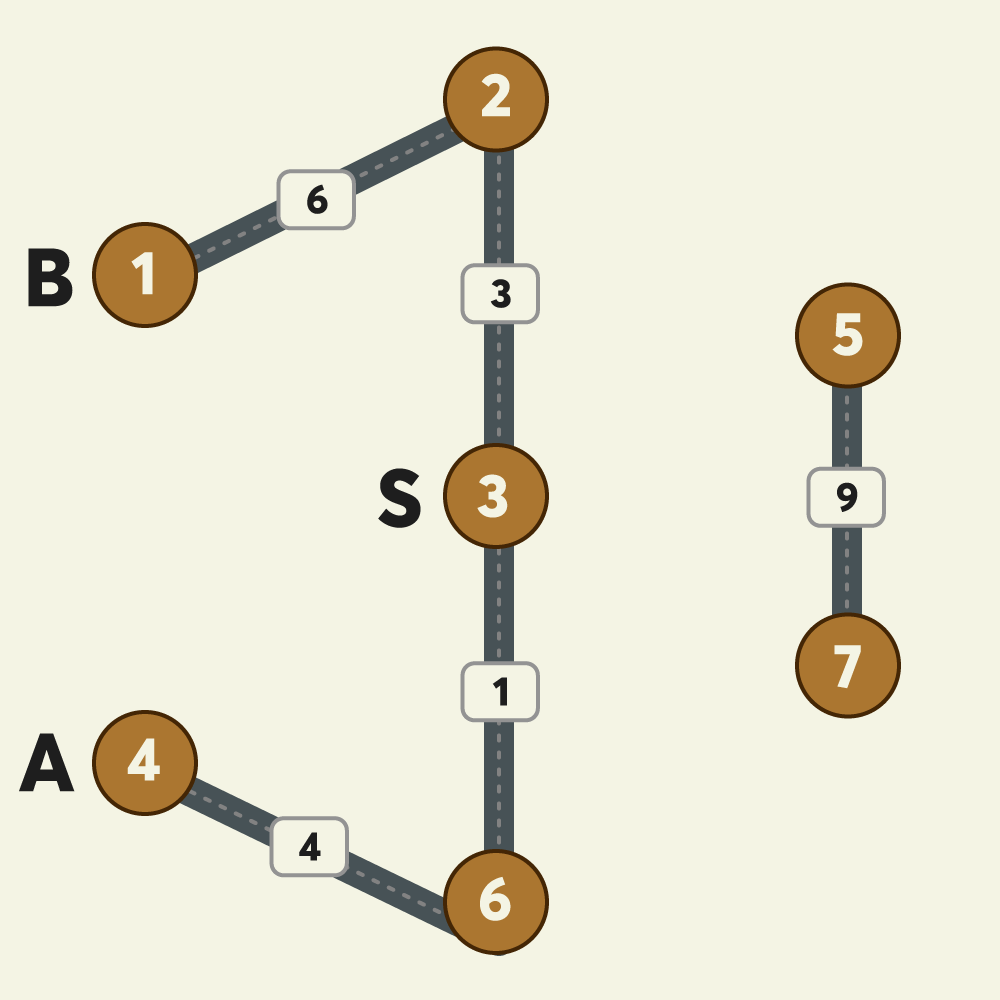
- 합승을 하지 않고, B는 3→2→1, A는 3→6→4 경로로 각자 택시를 타고 가는 것이 최저 예상 택시요금입니다.
- 따라서 최저 예상 택시요금은 (3 + 6) + (1 + 4) = 14원 입니다.
입출력 예 #3
- A와 B가 4→6 구간을 합승하고 B가 6번 지점에서 내린 후, A가6→5` 구간을 혼자 타고 가는 것이 최저 예상 택시요금입니다.
- 따라서 최저 예상 택시요금은 7 + 11 = 18원 입니다.
나의 풀이
package programmers;
public class SharedTaxiFare {
public static final int INF = 10_000_000;
public static int solution(int n, int s, int a, int b, int[][] fares) {
int[][] graph = new int[n+1][n+1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(i == j) graph[i][j] = 0;
else graph[i][j] = INF;
}
}
for(int[] fare : fares) {
int x = fare[0];
int y = fare[1];
int fee = fare[2];
graph[x][y] = fee;
graph[y][x] = fee;
}
for(int k = 1; k <= n; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(graph[i][k] != INF && graph[k][j] != INF){
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}
}
}
}
int minFare = graph[s][a] + graph[s][b];
for(int i = 1; i <= n; i++) {
minFare = Math.min(minFare, graph[s][i] + graph[i][a] + graph[i][b]);
}
return minFare;
}
public static void main(String[] args) {
int[][] fares = {{4, 1, 10}, {3, 5, 24}, {5, 6, 2}, {3, 1, 41}, {5, 1, 24}, {4, 6, 50},
{2, 4, 66}, {2, 3, 22}, {1, 6, 25}};
solution(6, 4, 6, 2, fares);
}
}
나의 생각
서로의 노드가 연결되어 있고, 특정 노드 A에서 특정 노드 B까지의 비용(가중치)이 있는 것으로 보고 BFS를 떠올렸다. 하지만 문뜩, 며칠전에 공부했던 플로이드 와샬 알고리즘이 떠올랐다.특정 노드에서 노드까지 길이 없다면 이 값을 무한대로 두고, 자기자신에서 자신까지는 0으로 두며, 모든 노드 간의 최단 경로(최소 비용)가 필요한 경우 사용하기 좋은 알고리즘이였다.

INF값은 노드와 노드가 연결되어있지 않을 경우를 의미하며 제한사항을 보고 충분히 큰 값으로 설정한다.
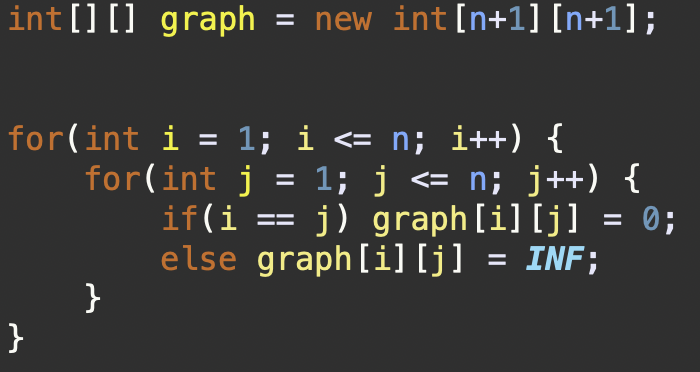
2차원 배열 grpah를 선언하며, 2차원 배열의 크기는 n+1 사이즈로 잡는다.
👉🏻 배열의 인덱스는 0부터 시작하지만, 문제에서 지점 번호가 1부터 시작하므로, 인덱스를 문제의 지점 번호에 맞추기 위해 배열의 크기를 n+1로 설정
if문에서는
i = j조건으로 자기 자신의 노드에서 자기 자신의 노드로 가는 것은0이며 다른 노드 간 걸리는 알려지지 않았으므로 무한대(INF)로 초기화한다.
초기 설정

경로 비용 설정
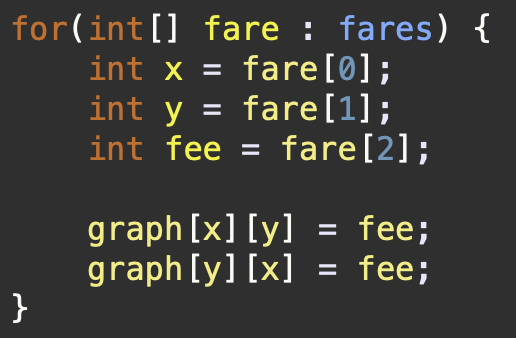
매개변수로 주어지는 fares는 x좌표, y좌표, 노선 비용을 의미한다.
가령,(2,1,10)이라는 fare 값이 있다고 할때,
graph[2][1]과 graph[1][2]는 같은 노선 비용을 가진다. (양방향 그래프에서 간선의 가중치가 양쪽 방향으로 동일함)
💡 플로이드 와샬 알고리즘(핵심)

플로이드 와샬 알고리즘의 시간 복잡도는 O(n^3)으로, 삼중 루프문으로 구성되어 있어, 제한사항의 n의 크기가 적당한지 먼저 파악해야한다. 위 문제에서 n의 크기는 최대 200이다.
if(graph[i][k] != INF && graph[k][j] != INF){
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}플로이드 와샬 알고리즘의 핵심 부분으로, 모든 노드 쌍 간의 최단 거리(최소 비용)을 계산하는 과정을 나타낸다. 여기서
graph배열은 각 노드 간의 최소 경로 비용을 저장하고 있으며INF는 두 노드 간에 경로가 없음을 의미한다.
if(graph[i][k] != INF && graph[k][j] != INF)조건문은 노드 i에서 k를 거쳐 j로 가는 경로가 실제로 존재하는지 확인하며, i에서 k까지의 경로와 k에서 j까지의 경로가 둘 다 존재할 때만, 그 경로를 사용하여 i에서 j까지의 거리를 갱신할 수 있음
모든 순회를 종료한 시점에서의 배열 값
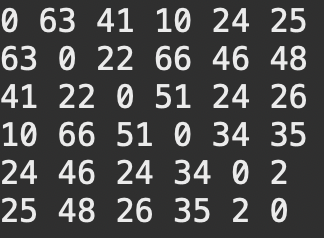
현재의 2차원 배열에는 각 쌍 노드의 택시 최소 운행 비용이 최신화되어있다.
이 2차원 배열에서, 배열의 행과 열은 각각 출발 노드와 도착 노드를 나타내고, 배열의 각 위치에 있는 값은 해당 노드 쌍을 연결하는 최소 비용을 의미한다. 예를 들어, graph[1][2]는 노드 1에서 노드 2로 가는 최소 비용을, graph[2][1]은 노드 2에서 노드 1로 가는 최소 비용을 나타낸다.
내가 고민했던 점
매개변수로 주어진 `s, a, b`를 가지고 s → a , s → b 따로 가는게 나은지,
s → 합승 구간 → a, s → 합승 구간 → b
즉, 합승 후 목적지까지 따로 가는게 나은지 어떻게 판별 할 것인가?💡 진짜 핵심 로직

알고보면 이미 플로이드 와샬 알고리즘에서 각 노드 간의 최소 비용을 이미 계산하였음
예를들어,s = 4, a = 6, b = 2라 할때
int minFare = graph[4][6] + graph[4][2]
graph[s][i] + graph[i][a] + graph[i][b]
graph[s][i]는 시작점 4번에서 합승 지점 i까지의 비용graph[i][a]는 합승 지점 i에서 A의 목적지인 6번까지 가는 비용graph[i][b]는 합승 지점 i에서 B의 목적지인 2번까지 가는 비용즉,
minFare와graph[s][i] + graph[i][a] + graph[i][b]를 비교하여 더 작은 값이 최소 비용이다.
