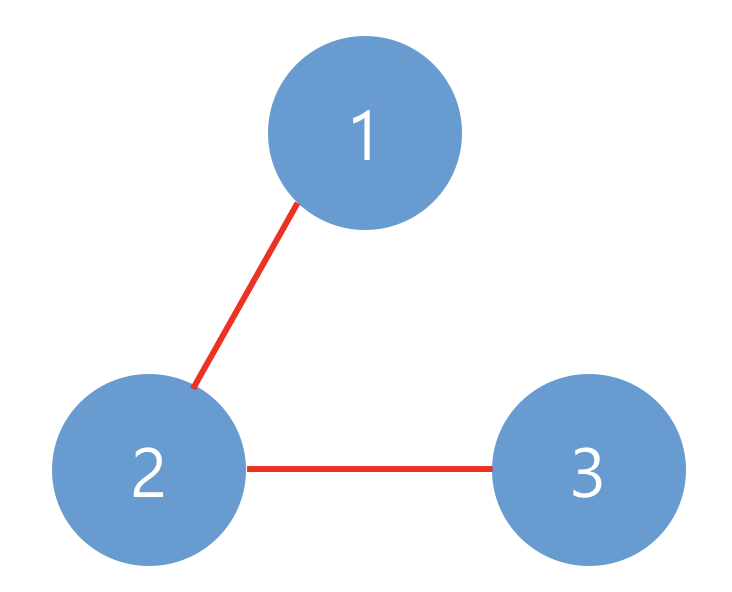
네트워크
문1) 네트워크란 컴퓨터 상호 간에 정보를 교환할 수 있도록 연결된 형태를 의미합니다. 예를 들어, 컴퓨터 A와 컴퓨터 B가 직접적으로 연결되어있고, 컴퓨터 B와 컴퓨터 C가 직접적으로 연결되어 있을 때 컴퓨터 A와 컴퓨터 C도 간접적으로 연결되어 정보를 교환할 수 있습니다. 따라서 컴퓨터 A, B, C는 모두 같은 네트워크 상에 있다고 할 수 있습니다.
컴퓨터의 개수 n, 연결에 대한 정보가 담긴 2차원 배열 computers가 매개변수로 주어질 때, 네트워크의 개수를 return 하도록 solution 함수를 작성하시오.
제한사항
- 컴퓨터의 개수 n은 1 이상 200 이하인 자연수입니다.
- 각 컴퓨터는 0부터 n-1인 정수로 표현합니다.
- i번 컴퓨터와 j번 컴퓨터가 연결되어 있으면 computers[i][j]를 1로 표현합니다.
- computer[i][i]는 항상 1입니다.
입출력 예
| n | computers | return |
|---|---|---|
| 3 | [[1, 1, 0], [1, 1, 0], [0, 0, 1]] | 2 |
| 3 | [[1, 1, 0], [1, 1, 1], [0, 1, 1]] | 1 |
입출력 예 설명
예제 #1
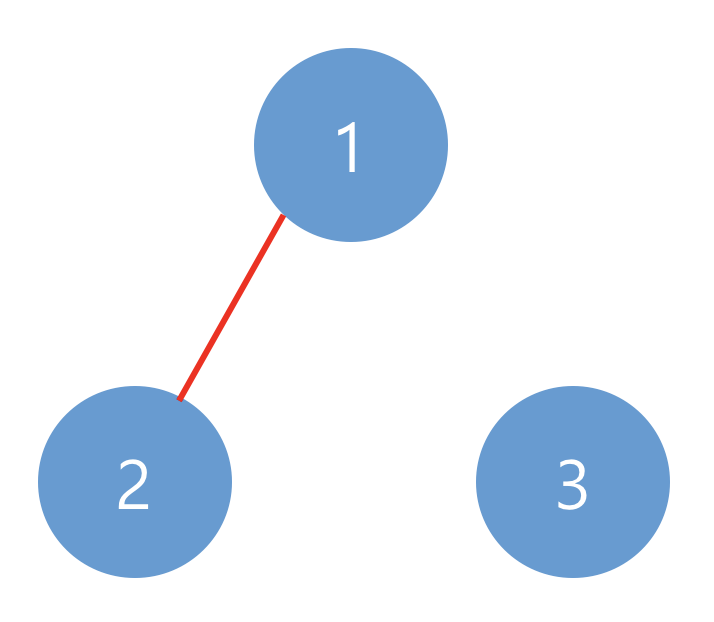
예제 #2
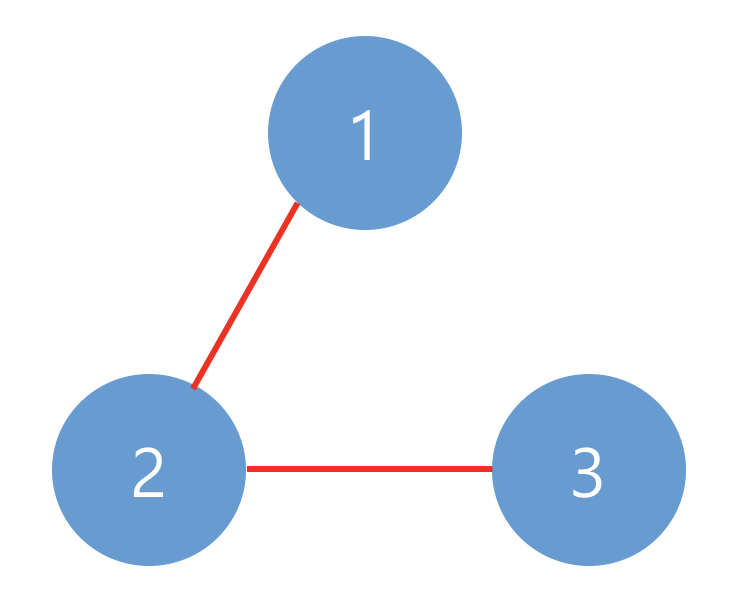
나의 풀이
visited 1차원 배열, map 2차원 배열 사용
package programmers;
public class Network {
static boolean[][] map;
static boolean[]visited;
static int n;
public static void dfs(int node) {
visited[node] = true;
for(int i = 0; i < n; i++) {
if(map[node][i] && !visited[i]) {
dfs(i);
}
}
}
public static int solution(int n, int[][] computers) {
Network.n = n;
map = new boolean[n][n];
visited = new boolean[n];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
map[i][j] = computers[i][j] == 1;
}
}
int answer = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
dfs(i);
answer++;
}
}
System.out.println(answer);
return answer;
}
public static void main(String[] args) {
int n = 3;
int[][] computers = {{1, 1, 0}, {1, 1, 0}, {0, 0, 1}};
solution(n, computers);
}
}
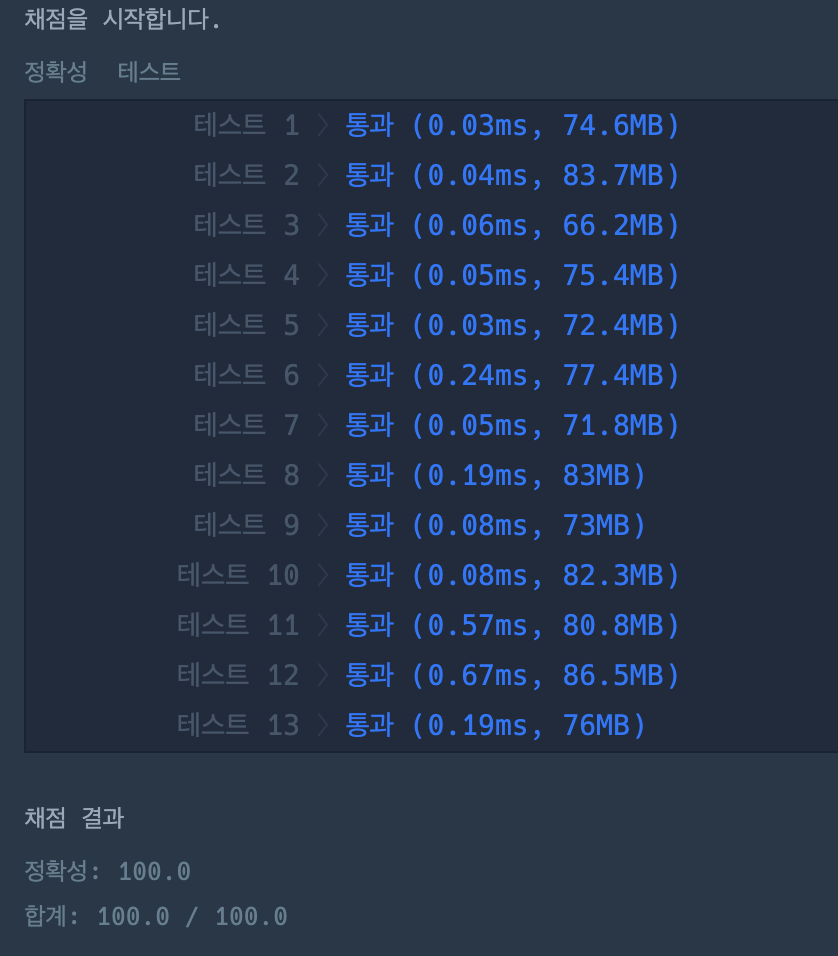
visited 1차원 배열을 쓰지 않는 방법
package programmers;
public class Network {
static int n;
public static void dfs(int node, int[][] computers) {
for (int i = 0; i < n; i++) {
if (computers[node][i] == 1) {
computers[node][i] = 0; // 방문한 노드를 0으로 표시
dfs(i, computers);
}
}
}
public static int solution(int n, int[][] computers) {
Network.n = n;
int answer = 0;
for (int i = 0; i < n; i++) {
if (computers[i][i] == 1) {
dfs(i, computers);
answer++;
}
}
return answer;
}
public static void main(String[] args) {
int n = 3;
int[][] computers = {{1, 1, 0}, {1, 1, 0}, {0, 0, 1}};
solution(n, computers);
}
}
나의 생각
문제를 보다가 dfs로 문제를 해결할 수 있겠다고 생각했는데, 어디서 많이 본 문제여서 확인해보니 [백준 11724 연결 요소의 개수](https://www.acmicpc.net/problem/11724)와 문제는 다르지만 푸는 방법이 아주 흡사했던 것 같다.
내가 부족한 부분이 dfs/dfs 라고 생각하여, dfs 관련 인강도 찾아보고, 관련 문제를 여러개 풀다보니 비슷한 유형의 문제가 눈에 들어온것 같다.
내가 생각한 풀이는 다음과 같다.
- 매개변수로 주어진 연결 정보를 map 2차원 배열에 넣자. ( 매개변수를 직접 활용하는 방법도 있음)
int[][] computers = {{1, 1, 0}, {1, 1, 0}, {0, 0, 1}};
위 정보에서 알 수 있는 내용은
2차원 배열 좌표계로 보면 y좌표, x좌표를 알 수 있다.
{1,1,0}은 y = 0, x = 0 일때 이 값은 1
y = 0, x = 1 일때 이 값은 1
y = 0, x = 2 일때 이 값은 0
{1,1,0}은 y = 1, x = 0 일때 이 값은 1
y = 1, x = 1 일때 이 값은 1
y = 1, x = 2 일때 이 값은 0
y = 2, x = 0 일때 이 값은 0
y = 2, x = 1 일때 이 값은 0
y = 2, x = 2 일때 이 값은 1
을 의미한다.여기서 컴퓨터 1, 2, 3이 존재할 때, 배열의 index(java 배열의 index는 0번부터 시작하기때문)를 좌표랑 일치시키기 위해 각 좌표 +1을 한다.
y,x 좌표에 +1을 해서 컴퓨터 번호와 일치 시킨다.
y = 1, x = 1 일때 이 값은 1 (computer[i][i]는 항상 1 = 자기 자신)
y = 1, x = 2 일때 이 값은 1
y = 1, x = 3 일때 이 값은 0
y = 2, x = 1 일때 이 값은 1
y = 2, x = 2 일때 이 값은 1 (computer[i][i]는 항상 1 = 자기 자신)
y = 2, x = 3 일때 이 값은 0
y = 3, x = 1 일때 이 값은 0
y = 3, x = 2 일때 이 값은 0
y = 3, x = 3 일때 이 값은 1 (computer[i][i]는 항상 1 = 자기 자신)매개변수의 내용을 바탕으로 위 내용을 표에 넣으면 다음과 같다.
표의 1은 true(연결O), 0은 false(연결X)를 의미한다.
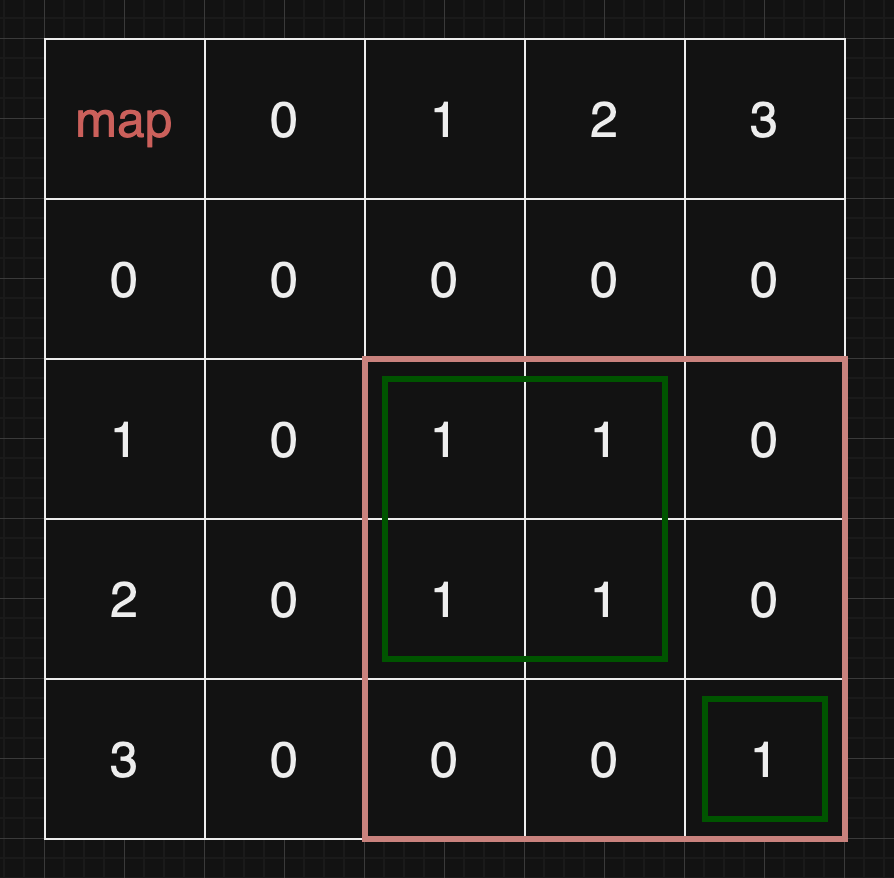
즉, 두개의 네트워크가 존재함을 표로 확인할 수 있다.
- 그렇다면, 어떻게 재방문을 방지할 수 있을까?
- visited 배열을 사용하여 방문하면 true, 방문하지 않으면 false값으로 나타내기
방문 전

방문 후

- 동작 순서는 어떻게?
- 이번 문제의 핵심은 예를들어
1번과 연결된 컴퓨터가 몇대인가?가 아닌, 서로 연결된 네트워크를 묻는 질문이므로, 모든visited배열을 방문해야하는 것이다.
1번 컴퓨터는 먼저 자기 자신에서 시작 (visited[1] = true)
map에서 1번 컴퓨터가 연결된 컴퓨터가 어디인지 탐색
1번 컴퓨터가 2번 컴퓨터와 연결돼있기때문에 2번으로 이동 (visited[2] = true)
2번은 1번과 연결돼있고, 이미 한번 방문 했기때문에 dfs를 종료 (answer 1증가)
다시 3번부터 dfs가 동작하고, 3번은 자기자신이랑만 연결돼있기때문에 dfs종료 (answer 1증가)
최종적으로 answer = 2야근 지수
문2) 회사원 Demi는 가끔은 야근을 하는데요, 야근을 하면 야근 피로도가 쌓입니다. 야근 피로도는 야근을 시작한 시점에서 남은 일의 작업량을 제곱하여 더한 값입니다. Demi는 N시간 동안 야근 피로도를 최소화하도록 일할 겁니다.Demi가 1시간 동안 작업량 1만큼을 처리할 수 있다고 할 때, 퇴근까지 남은 N 시간과 각 일에 대한 작업량 works에 대해 야근 피로도를 최소화한 값을 리턴하는 함수 solution을 완성해주세요.
제한 사항
- works는 길이 1 이상, 20,000 이하인 배열입니다.
- works의 원소는 50000 이하인 자연수입니다.
- n은 1,000,000 이하인 자연수입니다.
입출력 예
| works | n | result |
|---|---|---|
| [4,3,3] | 4 | 12 |
| [2,1,2] | 1 | 6 |
| 1,1 | 3 | 0 |
입출력 예 설명
입출력 예 #1
n=4 일 때, 남은 일의 작업량이 [4, 3, 3] 이라면 야근 지수를 최소화하기 위해 4시간동안 일을 한 결과는 [2, 2, 2]입니다. 이 때 야근 지수는 22 + 22 + 22 = 12 입니다.
입출력 예 #2
n=1일 때, 남은 일의 작업량이 [2,1,2]라면 야근 지수를 최소화하기 위해 1시간동안 일을 한 결과는 [1,1,2]입니다. 야근지수는 12 + 12 + 22 = 6입니다.
입출력 예 #3
남은 작업량이 없으므로 피로도는 0입니다.
나의 풀이
package programmers;
import java.util.Comparator;
import java.util.PriorityQueue;
public class OvertimeIndex {
public static long solution(int n, int[] works) {
PriorityQueue<Integer> priorityWork = new PriorityQueue<>(Comparator.reverseOrder());
for(int work : works) {
priorityWork.add(work);
}
while( n > 0 && !priorityWork.isEmpty()) {
int priorWork = priorityWork.poll();
if(priorWork > 0) {
priorityWork.add(priorWork - 1);
n--;
}
}
System.out.println(priorityWork);
long overtimeIndex = 0;
while(!priorityWork.isEmpty()) {
int work = priorityWork.poll();
overtimeIndex += (long) work * work;
}
System.out.println(overtimeIndex);
return overtimeIndex;
}
public static void main(String[] args) {
int n = 1;
int[] works = {2,1,2};
solution(n, works);
}
}
나의 생각
문제를 보며, 제한 사항을 보는데, 막연하게 떠오르는 생각은 brute Force 와 Greedy 알고리즘 이였다.
제한 사항을 보면 알 수 있듯이, 완전 탐색으로는 제한 시간 안에는 풀 수 없겠다라고 생각들면서도, 내가 원하는 답이 나오면 break나, return으로 빠져나오면 되니 시간이 단축될꺼라 생각했다.
내가 제일 처음 한 생각은 n을 int[] works 배열의 크기에 맞게 분배하는것이다.
예를들어 n = 4, works 배열의 크기가 3일 때를 먼저 보자.
해당되는 경우의 수
{4, 0, 0}
{3, 1, 0}
{3, 0, 1}
{2, 2, 0}
{2, 0, 2}
{2, 1, 1} - > 야근 지수가 최소가 될 때의 경우
{1, 2, 1}
{1, 1, 2}
...
{0, 0, 4}위 경우의 수는 최악의 경우라 해봐야 15번째에 답을 도출할 수 있지만, 경우가 커지면 커질수록 기하급수적으로 그 경우의 수는 증가한다. 따라서 문제에 주어진 예만 보고 판단할 것이 아니라
제한사항을 면밀히 검토한 뒤 로직을 설계하는 것이 우선이였다. 나의 경우는 재귀로 n = 4이고, 배열의 크기가 3일 때 만들 수 있는 경우의수를 재귀적으로 조합하는 메서드를 만드는 연습을 하기위해서였지만, 이 조차도 쉽지않았다.
package programmers;
import java.util.Arrays;
public class OvertimeIndex {
public static void findDistribution(int n, int size, int[]distribution, int index) {
if(index == size - 1) {
distribution[index] = n;
System.out.println(Arrays.toString(distribution));
return;
}
for(int i = 0; i <= n; i++) {
distribution[index] = i;
findDistribution(n - i, size, distribution, index + 1);
}
}
public static long solution(int n, int[] works) {
int size = works.length;
int[] distribution = new int[size];
findDistribution(n, size, distribution, 0);
return 0;
}
public static void main(String[] args) {
int n = 4;
int[] works = {3,2,2};
solution(n, works);
}
}
위 로직을 실행하면 다음과 같은 조합을 얻을 수 있다.
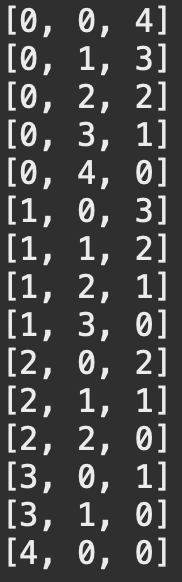
위 경우는 크기가 매우 작은 경우임에도 불구하고 15가지의 경우를 가진다.
그래서 나는 조합까지만 구하고 위 문제를 다시 탐욕법으로 풀고자 로직을 다시 설계했다.
- 우선 순위 큐를 생성하여 큐에 works의 원소값을 넣음

이때, Comparator.reverseOrder()은 정렬은 하는데 내림차순으로 한다는 의미이다.
즉, 잔업량이 가장 많은(큰) 순서로 나열된다는 의미이다.
n = 4일때

n > 0과 우선 순위 큐에 든 원소가 존재할 때 까지 반복 수행
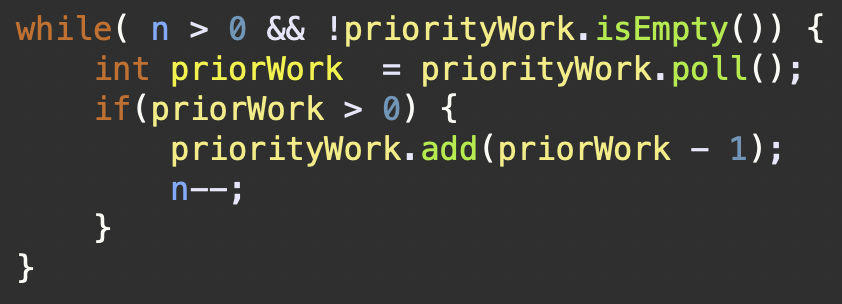
- 위 값에서 내림차순으로 정렬된 우선순위 큐에서 `poll()`을 수행하면 `4`가 나온다.
- 이때의 `int priorWork = 4`를 저장하고
- `priorWork > 0` 조건을 만족하면, `priorWork - 1` 을 하여 우선순위 큐에 다시. 넣는다.
- 그리고, `n`의 값을 `-1` 감소시킨다.n = 3 일때

n = 2 일때

n = 1 일때

n = 0 일때

남은 시간이 0이되면(야근에 쓸 시간을 모두 소진하면) 최종적으로 남은 작업량만 남게된다.
- 배열값을 바탕으로 야근지수 구하기
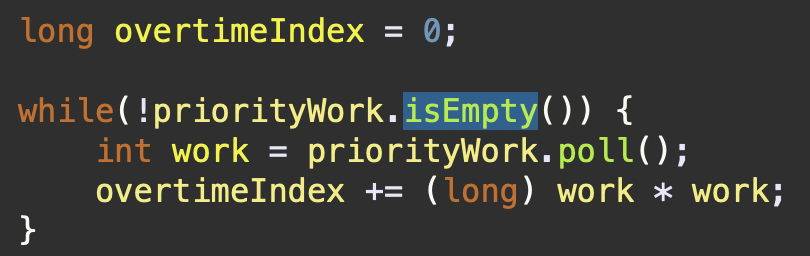
overtimeIndex의 long의 데이터 타입을 갖는데, 이는 int형의 데이터 크기를 초과할 수 있음을 시사한다(힌트)
위 로직으로 최종적으로 가공이 완료된 priorityWork에서 값을 하나씩 빼고, 그 값을 제곱한 것을 차례로 더하면 우리가 구하고자하는 overtimeIndex를 도출할 수 있게된다.
느낌점
위 문제를 완전 탐색과 그리드 알고리즘 측면에서 보면, 완전 탐색은 모든 조합을 고려해야한다. 하지만, 그리드 알고리즘은 현재에 할 수 있는 로컬 최적해를 도출해냄으로써 전역 최적해를 구할 수 있었으므로 완전탐색보다 빠른 시간으로 답을 도출할 수있었다. 탐욕법을 쓰면서 우선순위 큐 자료 구조를 활용하였는데, 이는 우선 순위 큐에서 가장 큰 작업량을 우선적으로 감소시키는 것이 문제의 핵심 로직이였기 때문이다.
최고의 집합
문3) 자연수 n 개로 이루어진 중복 집합(multi set, 편의상 이후에는 "집합"으로 통칭) 중에 다음 두 조건을 만족하는 집합을 최고의 집합이라고 합니다.
- 각 원소의 합이 S가 되는 수의 집합
- 위 조건을 만족하면서 각 원소의 곱 이 최대가 되는 집합
예를 들어서 자연수 2개로 이루어진 집합 중 합이 9가 되는 집합은 다음과 같이 4개가 있습니다.
{ 1, 8 }, { 2, 7 }, { 3, 6 }, { 4, 5 }
그중 각 원소의 곱이 최대인 { 4, 5 }가 최고의 집합입니다.
집합의 원소의 개수 n과 모든 원소들의 합 s가 매개변수로 주어질 때, 최고의 집합을 return 하는 solution 함수를 완성해주세요.
제한사항
- 최고의 집합은 오름차순으로 정렬된 1차원 배열(list, vector) 로 return 해주세요.
- 만약 최고의 집합이 존재하지 않는 경우에 크기가 1인 1차원 배열(list, vector) 에 -1 을 채워서 return 해주세요.
- 자연수의 개수 n은 1 이상 10,000 이하의 자연수입니다.
- 모든 원소들의 합 s는 1 이상, 100,000,000 이하의 자연수입니다.
입출력 예
| n | s | result |
|---|---|---|
| 2 | 9 | [4,5] |
| 2 | 1 | [-1] |
| 2 | 8 | [4,4] |
입출력 예 설명
입출력 예 #2
- 자연수 2개를 가지고는 합이 1인 집합을 만들 수 없습니다. 따라서 -1이 들어있는 배열을 반환합니다.
입출력 예 #3
-
자연수 2개로 이루어진 집합 중 원소의 합이 8인 집합은 다음과 같습니다.
-
{ 1, 7 }, { 2, 6 }, { 3, 5 }, { 4, 4 }
-
그중 각 원소의 곱이 최대인 { 4, 4 }가 최고의 집합입니다.
나의 풀이
효율성 테스트 실패 로직
package programmers;
import java.util.Arrays;
import java.util.PriorityQueue;
public class BestSet {
public static int[] solution(int n, int s) {
PriorityQueue<Integer> bestPick = new PriorityQueue<>();
int middleNum = s / n;
if(middleNum == 0) return new int[] {-1};
for(int i = 0; i < n; i++) {
bestPick.add(middleNum);
s -= middleNum;
}
while(s > 0) {
if(!bestPick.isEmpty()) {
int temp = bestPick.poll() + 1;
bestPick.add(temp);
s--;
}
}
int[] answer = new int[n];
for(int i = 0; i < answer.length; i++) {
if(!bestPick.isEmpty()) {
answer[i] = bestPick.poll();
}
}
System.out.println(Arrays.toString(answer));
return answer;
}
public static void main(String[] args) {
solution(10, 11);
}
}
int[] answer 배열을 직접 사용한 로직
package programmers;
import java.util.Arrays;
public class BestSet {
public static int[] solution(int n, int s) {
if(s < n) return new int[] {-1};
int[] answer = new int[n];
Arrays.fill(answer, s / n);
int remainder = s % n;
for(int i = n - 1; i >= n - remainder; i--) {
answer[i]++;
}
return answer;
}
public static void main(String[] args) {
solution(3, 11);
}
}
단어 변환
문4) 두 개의 단어 begin, target과 단어의 집합 words가 있습니다. 아래와 같은 규칙을 이용하여 begin에서 target으로 변환하는 가장 짧은 변환 과정을 찾으려고 합니다.
1. 한 번에 한 개의 알파벳만 바꿀 수 있습니다.
2. words에 있는 단어로만 변환할 수 있습니다.예를 들어 begin이 "hit", target가 "cog", words가 ["hot","dot","dog","lot","log","cog"]라면 "hit" -> "hot" -> "dot" -> "dog" -> "cog"와 같이 4단계를 거쳐 변환할 수 있습니다.
두 개의 단어 begin, target과 단어의 집합 words가 매개변수로 주어질 때, 최소 몇 단계의 과정을 거쳐 begin을 target으로 변환할 수 있는지 return 하도록 solution 함수를 작성해주세요.
제한사항
- 각 단어는 알파벳 소문자로만 이루어져 있습니다.
- 각 단어의 길이는 3 이상 10 이하이며 모든 단어의 길이는 같습니다.
- words에는 3개 이상 50개 이하의 단어가 있으며 중복되는 단어는 없습니다.
- begin과 target은 같지 않습니다.
- 변환할 수 없는 경우에는 0를 return 합니다.
입출력 예
| begin | target | words | return |
|---|---|---|---|
hit | cog | ["hot", "dot", "dog", "lot", "log", "cog"] | 4 |
hit | cog | ["hot", "dot", "dog", "lot", "log"] | 0 |
입출력 예 설명
예제 #2
- target인
cog는 words 안에 없기 때문에 변환할 수 없습니다.
나의 풀이
DFS 풀이
package programmers;
import java.util.Arrays;
public class WordConversion {
public static int transform(String begin, String target, String[] words, boolean[] visited) {
if(begin.equals(target)) return 0;
int minSteps = Integer.MAX_VALUE;
for (int i = 0; i < words.length; i++) {
if (!visited[i] && oneCharDiff(begin, words[i])) {
visited[i] = true;
int steps = transform(words[i], target, words, visited);
if (steps != Integer.MAX_VALUE) {
minSteps = Math.min(minSteps, steps + 1);
}
visited[i] = false;
}
}
return minSteps;
}
public static boolean oneCharDiff(String a, String b) {
int count = 0;
for (int i = 0; i < a.length(); i++) {
if (a.charAt(i) != b.charAt(i)) count++;
}
return count == 1;
}
public static int solution(String begin, String target, String[] words) {
if(!Arrays.asList(words).contains(target)) return 0;
boolean[] visited = new boolean[words.length];
int steps = transform(begin, target, words, visited);
System.out.println(steps);
return steps == Integer.MAX_VALUE ? 0 : steps;
}
public static void main(String[] args) {
String begin = "hit";
String target = "cog";
String[] words = {"hot", "dot", "dog", "lot", "log", "cog"};
solution(begin, target, words);
}
}BFS 풀이
package programmers;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class WordConversion {
static class Pair {
String word;
int depth;
public Pair(String word, int depth) {
this.word = word;
this.depth = depth;
}
}
public static boolean canTransform(String word1, String word2) {
int count = 0;
for(int i = 0; i < word1.length(); i++) {
if (word1.charAt(i) != word2.charAt(i)) {
count++;
if (count > 1) {
return false;
}
}
}
return count == 1;
}
public static int solution(String begin, String target, String[] words) {
if(!Arrays.asList(words).contains(target)) return 0;
Queue<Pair> queue = new LinkedList<>();
boolean[] visited = new boolean[words.length];
queue.add(new Pair(begin, 0));
while(!queue.isEmpty()) {
Pair current = queue.poll();
String currentWord = current.word;
int currentDepth = current.depth;
if(currentWord.equals(target)) {
return currentDepth;
}
for (int i = 0; i < words.length; i++) {
if (!visited[i] && canTransform(currentWord, words[i])) {
visited[i] = true;
queue.add(new Pair(words[i], currentDepth + 1));
}
}
}
return 0;
}
public static void main(String[] args) {
String begin = "hit";
String target = "cog";
String[] words = {"hot", "dot", "dog", "lot", "log", "cog"};
solution(begin, target, words);
}
}나의 생각
DFS

매개변수로 주어진 target 단어가 words 배열에 없다면
변환할 수 없으므로 0을 반환한다.
기본적으로 BFS는 방문을 했는지 안했는지 추적하기 위해 배열을 선언한다.
boolean[] visited = new boolean[words.length];
transform 함수를 호출하여 최소 단계 수를 계산한다.
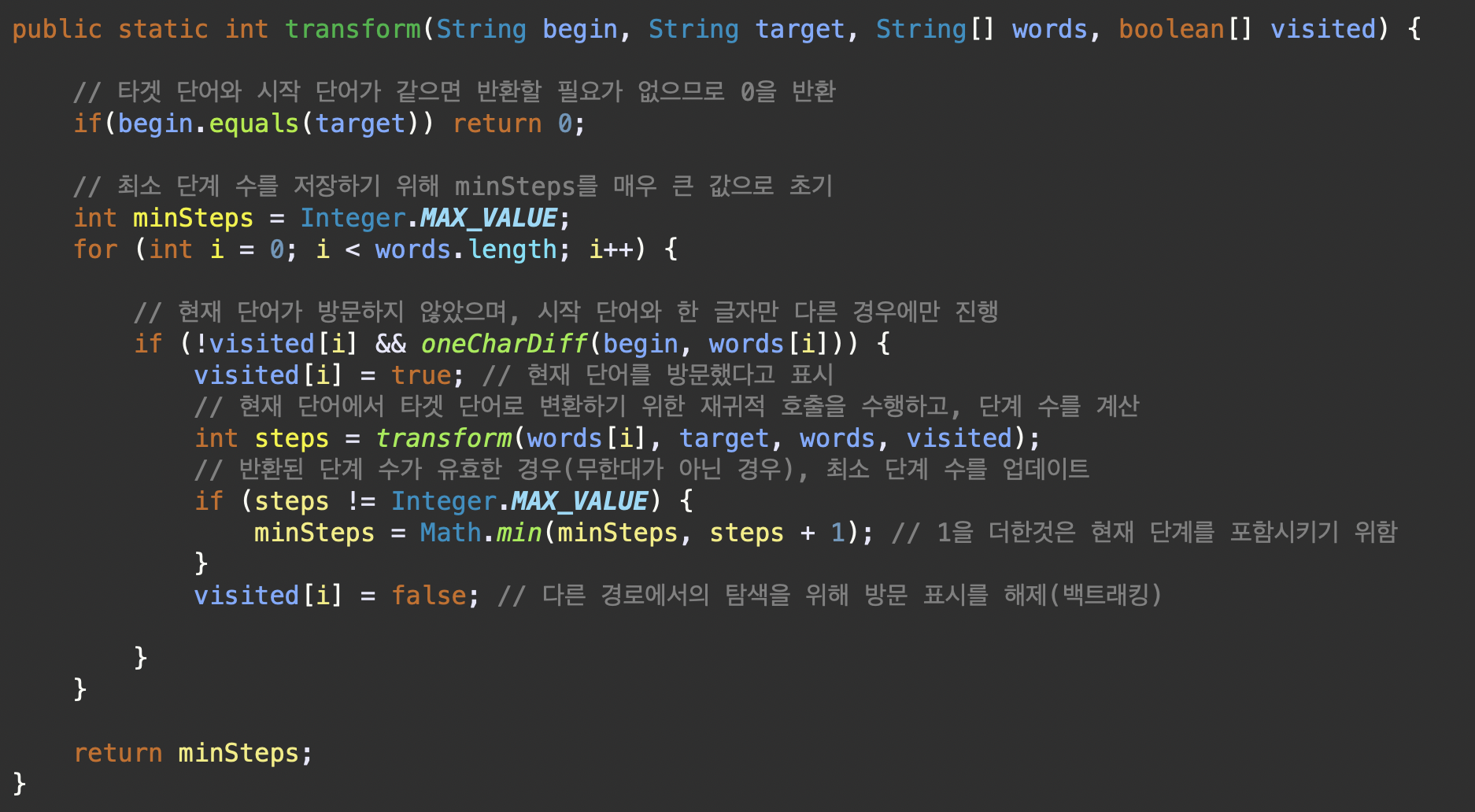
BFS
기본적인 BFS(Breadth First Search, 너비 우선 탐색)은 시작 노드에서 시작하여 인접합 노드를 먼전 탐색하는 방식이다. 일반적으로 Queue 인터페이스를 사용하여 구현하는데, Queue는 FIFO(First-In-First-Out, 선입선출)구조로, 먼저 들어온 요소가 먼저 나가는 특성을 가지고 있어서 BFS 구현에 적합하다.
BFS 알고리즘의 구현은 다음과 같은 단계를 포함한다.
1. Queue를 생성하고 시작노드를 큐에 넣는다.
2. visited 배열이나 Set을 사용하여 방문한 노드를 기록한다.
3. 큐가 비어있지 않은 동안 다음을 반복한다.
- 큐에서 노드를 dequeue한다
- 해당 노드를 방문 처리한다
- 해당 노드에 인접한 모드 노드에 대해, 방문하지 않았다면 큐에 넣고 방문 처리한다.- 먼저,
String[] words배열에target문자가 있는지 확인한다.


당연하게, words 배열안에 target 문자가 없다는 것은 아무리 변환해봐야 words 배열 내, target 문자가 없기때문에 0을 반환한다.
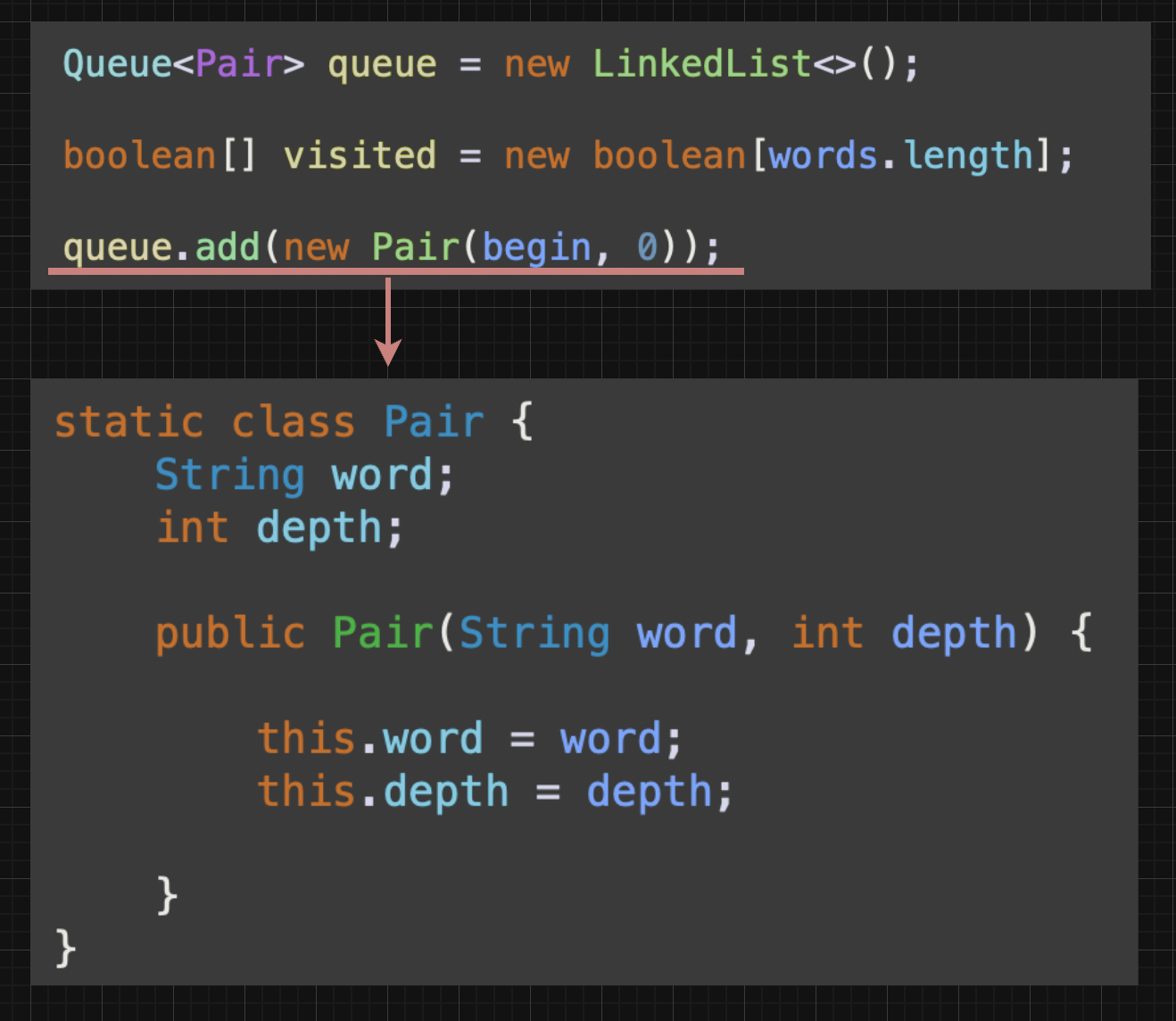

위와 같이 queue 자료 구조에 새로운 Pair 객체가 생성되고 그 안에 begin과 0이 들어가게 된다.
핵심 로직
while(!queue.isEmpty()) {
Pair current = queue.poll();
String currentWord = current.word;
int currentDepth = current.depth;
if(currentWord.equals(target)) {
return currentDepth;
}
for (int i = 0; i < words.length; i++) {
if (!visited[i] && canTransform(currentWord, words[i])) {
visited[i] = true;
queue.add(new Pair(words[i], currentDepth + 1));
}
}
}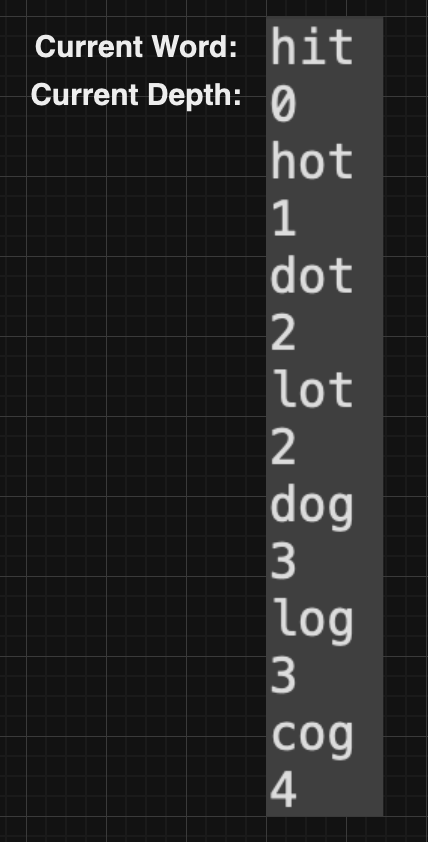
위 로직을 순서대로 나열하면 다음과 같다.
처음 큐에 담긴 내용은
hit, 0
if(currentWord.equals(target)) {
return currentDepth;
}
현재의 단어가 target 단어와 같은가?
- 같다면, 현재의 depth 0을 반환
- 그렇지않으면, if문을 건너뛴다.
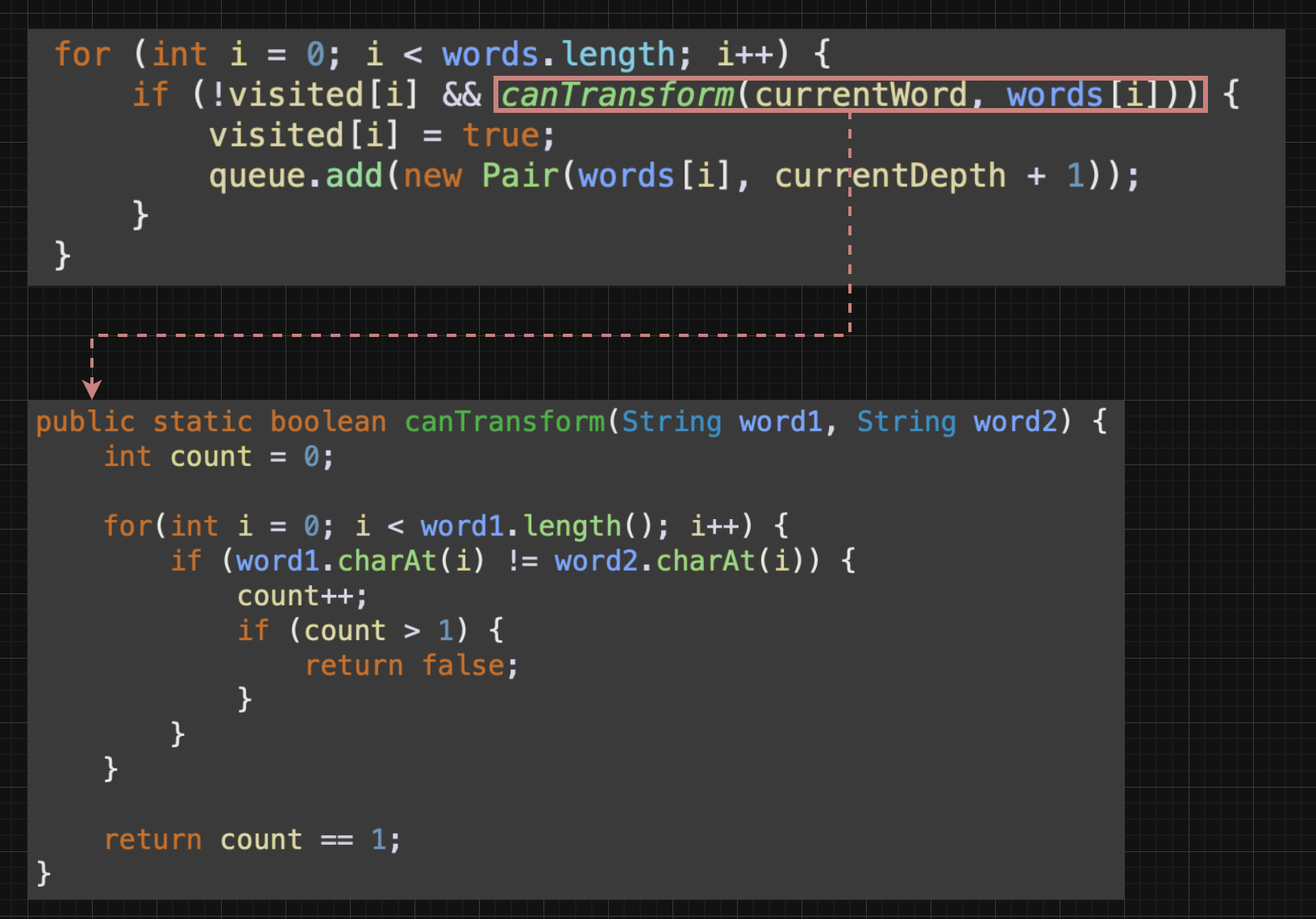
canTransform 메서드는 매개변수 word1, word2를 받아
두 문자를 비교하여 다른 글자가 몇개가 있는지 판별하는 로직이다.
예를들어,
word1 : hit, word2 : hot 일때
가운데 글자만 다르기때문에 count = 1이 된다.
즉, count = 1이면 true, 나머지는 false로 한 글자만 다르면 true를 반환하게된다.
if (!visited[i] && canTransform(currentWord, words[i])) {
의 두개의 명제 모두 참일 경우 (visited[i] 값이 false, canTransform 값이 true 일때)
1. 첫 번째 단계 (hit → hot)
- queue에서 Pair("hit", 0)을 꺼냄
- "hit"과 한 글자만 다른 단어는 "hot"이믈로 queue에 Pair("hot", 1)을 추가
2. 두 번째 단계(hot → dot, lot)
- queue에서 Pair("hot", 1)을 꺼냄
- "hot"와 한 글자만 다른 단어들은 "dot","lot"이므로, queue에 Pair("dot", 2)
Pair("lot", 2)를 추가
3. 세 번째 단계(dot → dog, lot → log)
- queue에서 Pair("dot", 2)을 꺼냄
- "dot"와 한 글자만 다른 단어는 "dog"이므로, Pair("dog", 3)을 추가
- queue에서 Pair("lot", 2)를 꺼냄
- "lot"와 한 글자만 다른 단어는 "log"이므로, Pair("log", 3)을 추가
4. 네 번째 단계(dog → cog, log → cog)
- queue에서 Pair("dog", 3)을 꺼냄
- "dog"와 한 글자만 다른 단어는 "cog"이므로, queue에 Pair("cog", 4)를 추가
- queue에서 Pair("log", 3)을 꺼냄
- "log"와 한 글자만 다른 단어도 "cog"이므로, queue에 Pair("cog", 4)를 추가
5. 최종 단계
- queue에서 Pair("cog", 4)를 꺼내고, currentWord가 target "cog"와 일치함을 확인, 이때의 currentDepth는 4이며, 이는 최소 변환 횟수를 의미함고찰
나는 두 가지 경우(DFS/BFS)로 모두 풀어봤는데
`words`의 길이가 크고 최단 경로를 찾는 것이
목적일 때는 BFS가 더 나은 선택같아 보였다.
DFS인 경우 모든 가능한 경로를 탐색하기 때문에, 최악의 경우 모든 단어를
방문할 때까지 깊게 들어갈 수 있으므로, 시간 복잡도는 O(N!)에 가까울수 있다.
이는 상태 공간 트리에서 모든 경로를 탐색하기 때문이며, DFS는 재귀적으로 구현되는
경우가 많아 호출 스택이 깊어질 수 있으며, 이는 스택 오버플로를 일으킬 위험이 있다.
반면, BFS는 각 단계에서 모든 가능한 변환을 단계별로
탐색(단어 하나를 변경할 때마다 새로운 단계로 넘어)하(가)므로,
최단 경로를 찾는 데에 효과적이다. BFS의 시간 복잡도는 O(N^2)이며
단어가 많아질수록 BFS가 훨씬 효율적이다.
단, 배열에 많은 단어가 서로 연결되지 않고 탐색 공간이 제한적인 경우
DFS가 더 효율적일 수 있기때문에 문제의 특성과 입력 데이터의 크기를 고려하여
알고리즘을 선택해야할꺼 같다.
등굣길
문5) 계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.
아래 그림은 m = 4, n = 3 인 경우입니다.
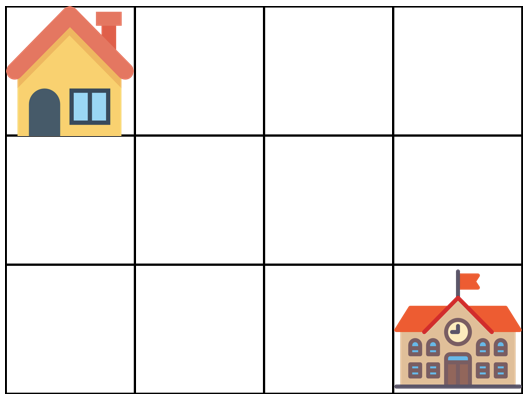
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.
격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
- m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
- 물에 잠긴 지역은 0개 이상 10개 이하입니다.
- 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.
입출력 예
| m | n | puddles | return |
|---|---|---|---|
| 4 | 3 | [[2,2]] | 4 |
입출력 예 설명
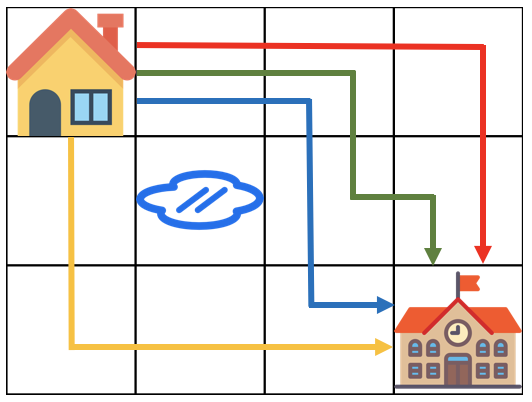
나의 풀이
package programmers;
public class OnTheWayToSchool {
public static final int MOD = 1_000_000_007;
public static int solution(int m, int n, int[][] puddles) {
int[][] dp = new int[n + 1][m + 1];
for(int[] puddle : puddles) {
dp[puddle[1]][puddle[0]] = -1;
}
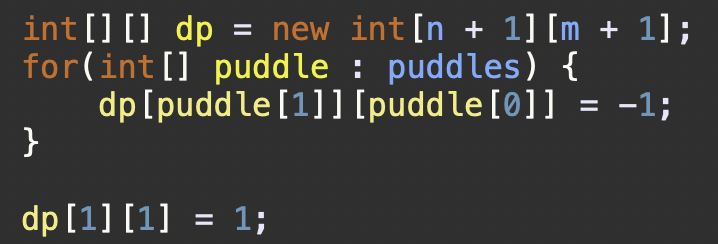
dp[1][1] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (dp[i][j] == -1) {
dp[i][j] = 0;
} else {
dp[i][j] += dp[i-1][j] % MOD;
dp[i][j] += dp[i][j-1] % MOD;
}
}
}
return dp[n][m] % MOD;
}
public static void main(String[] args) {
int m = 4;
int n = 3;
int[][] puddles = {{2,2}};
solution(m, n, puddles);
}
}
나의 생각
이번 문제를 보자마자 중고등학교 시절 수학시간에 배웠던 경우의 수(경로 계산 문제) 구하는 방법이 떠올랐다. 맵에서 장애물이 있는 곳을 0으로 채워 해당 지점의 한칸 왼쪽, 한칸 위쪽의 수를 더한 것이 그 지점까지 갈 수 있는 경우의 수를 나타낸다.
아래는 시작점과 끝점 사이 갈 수 있는 경우의 수를 나타낸 표다.
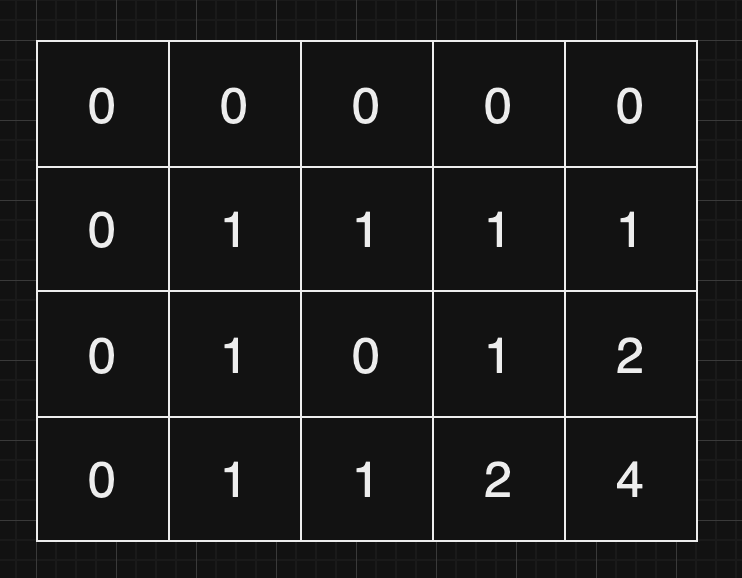
위 문제는 다이나믹 동적프로그래밍 알고리즘으로 쉽게 구현할 수 있는데, 먼저 2차원 dp 배열의 크기를 n + 1, m + 1만큼으로 잡아준다.
👉🏻 그 이유는,
1. 인덱스 조정: 자바에서는 배열의 인덱스는 보통 0부터 시작하는데, 이 문제에서는 격자의 위치를
1부터 시작하기 때문이다. (즉, 집의 위치 (1,1)) 배열의 인덱스를 1부터 시작하도록
조정함으로써, 문제 설명과 코드 내의 인덱스 사용을 직관적으로 일치시키기 위함이다.
2. 경계 조건 처리 : dp 배열의 추가된 행과 열(즉, 0번째 행과 열)은 경계 조건
처리를 용이하게 한다.
예를들어, dp[i][j]를 계산할 때 dp[i-1][j]와 dp[i][j-1]의 값을 사용하는데,
이러한 계산을 시작점에서도 적용할 수 있도록 하기 위함이다.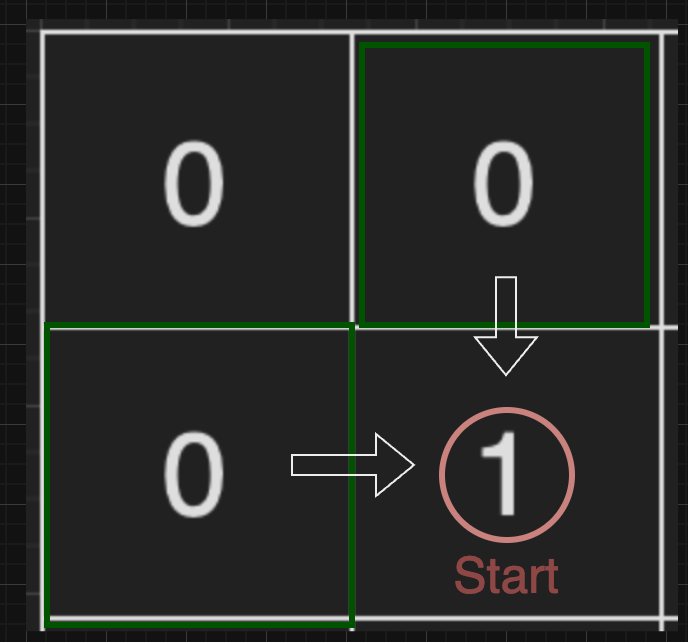

위 로직은 dp[i][j] == -1이면 웅덩이가 있는 곳이기 때문에 dp[i][j] = 0으로 하고
웅덩이가 없는 곳의 좌표에서는 해당 좌표의 한 칸 왼쪽, 한 칸 위쪽의 값을 더하여 경우의 수를 표현하였다.
💡 위 문제를 동적 프로그래밍을 사용한 이유가 있는것인가?
- 위 문제의 경우, 주어진 문제가 겹치는 하위 문제들로 구성되어 있고, 이러한 하위 문제들의 결과를 재활용할 수 있기 때문에
dp로 문제를 접근하였다.
dp를 사용하여 문제를 푸는 이유는 다음과 같다.
- 중복 계산의 제거 : 각 격자점까지의 경로 수는 한 번 계산되면 그 값이 변하지 않으므로,
한 번 계산한 값을 저장해두고 팔요할 때마다 재사용할 수 있음 👉🏻 계산 시간을 크게 줄여줌
- 하향식 접근법 : 격자의 시작점에서 출발하여 목적지에 도달할 때까지의 경로를 단계적으로
구축, 이는 각 단계에서 최적의 결정만을 취함으로써 최종적으로 최적의 해답을 도출
❗️ DFS 또는 BFS로는 풀 수 없는건가?
- 두 알고리즘으로도 문제를 풀 수 있지만, 이 경우 시간 복잡도가 증가할 수 있음
이는 격자의 각 점마다 가능한 모든 경로를 탐색해야 하기때문
특히, DFS는 모든 가능한 경로를 다 탐색해야 하므로, 경로의 수가 많은 경우
매우 비효율적임
| 알고리즘 | 시간 복잡도 | 메모리 사용량 | 특징 |
|---|---|---|---|
| DP | ( O(mn) ) | ( O(mn) ) | 최적화 문제에 적합, 재귀 호출 오버헤드 없음 |
| DFS/BFS | ( O(2^{m+n}) ) | BFS: 경로 수에 비례 | 모든 가능한 해를 찾을 때 사용 |
