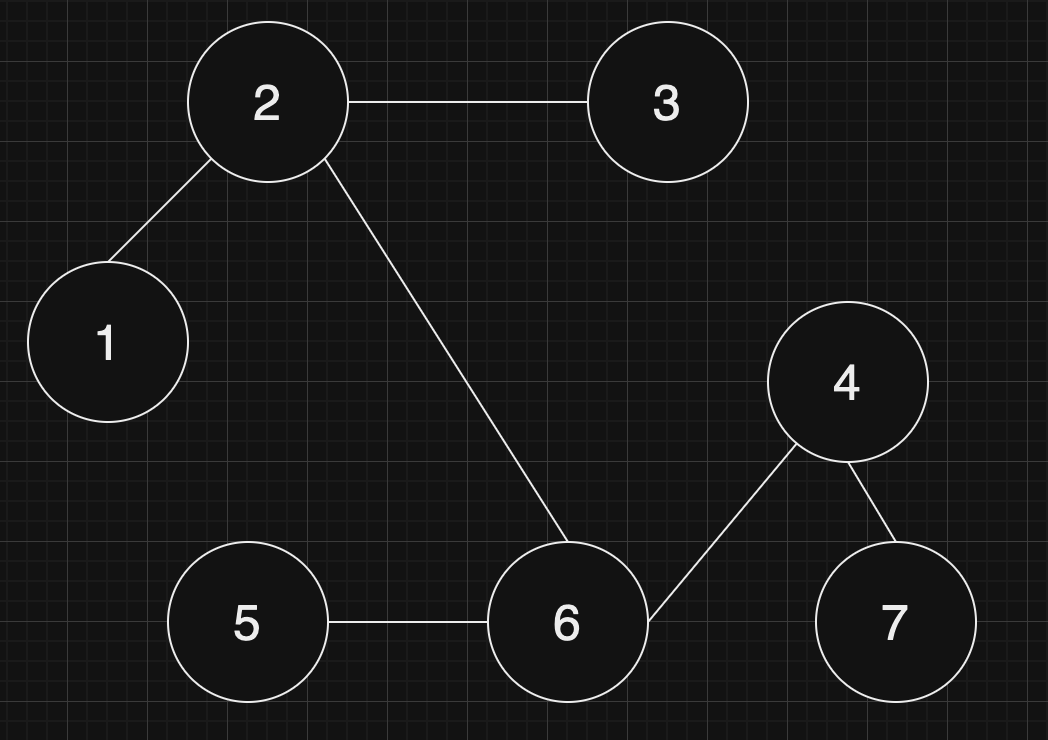
단속카메라
문1) 고속도로를 이동하는 모든 차량이 고속도로를 이용하면서 단속용 카메라를 한 번은 만나도록 카메라를 설치하려고 합니다.
고속도로를 이동하는 차량의 경로 routes가 매개변수로 주어질 때, 모든 차량이 한 번은 단속용 카메라를 만나도록 하려면 최소 몇 대의 카메라를 설치해야 하는지를 return 하도록 solution 함수를 완성하세요.
제한사항
- 차량의 대수는 1대 이상 10,000대 이하입니다.
- routes에는 차량의 이동 경로가 포함되어 있으며 routes[i][0]에는 i번째 차량이 고속도로 에 진입한 지점, routes[i][1]에는 i번째 차량이 고속도로에서 나간 지점이 적혀 있습니다.
- 차량의 진입/진출 지점에 카메라가 설치되어 있어도 카메라를 만난것으로 간주합니다.
- 차량의 진입 지점, 진출 지점은 -30,000 이상 30,000 이하입니다.
입출력 예
| routes | return |
|---|---|
[[-20,-15], [-14,-5], [-18,-13], [-5,-3]] | 2 |
입출력 예 설명
-5 지점에 카메라를 설치하면 두 번째, 네 번째 차량이 카메라를 만납니다.
-15 지점에 카메라를 설치하면 첫 번째, 세 번째 차량이 카메라를 만납니다.
나의 풀이
package programmers;
import java.util.Arrays;
import java.util.Comparator;
public class SurveillanceCamera {
public static int solution(int[][] routes) {
Arrays.sort(routes, Comparator.comparing(o -> o[1]));
int cameraCount = 0;
int cameraLocation = Integer.MIN_VALUE;
for(int[] route : routes) {
if(route[0] > cameraLocation) {
cameraCount++;
cameraLocation = route[1];
}
}
return cameraCount;
}
public static void main(String[] args) {
int[][] routes = {{-20,-15}, {-14,-5}, {-18,-13}, {-5,-3}};
solution(routes);
}
}
나의 생각
👉🏻 탐욕법 알고리즘 설명
탐욕법의 핵심은 정렬과 부분 최적화의 합이 전체 최적화가 되도록 설계하는것이다. 하지만, 모든 탐욕법 문제에서 정렬이 필요한 것은 아니며, 탐욕법이 효과적으로 작동하기 위해서는 두 가지 속성이 충족되어야 한다.
- 탐욕적 선택 속성 : 매 순간 최적이라고 생각되는 선택을 해도 최종 해답에 도달할 수 있어야 한다.
- 최적 부분 구조 (Optimal Substructure) : 문제에 대한 최적의 해답이 그 하위 문제에 대한 최적의 해답으로부터 구성될 수 있어야 한다.
- 해당
routes를 어떻게 정렬할 것인가?
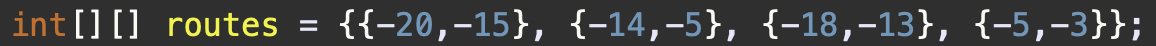
나는 고속도도를 나간 시점을 기준으로 먼저 정렬을 진행하였다.


즉, -15, -13, -5, -3 고속도를 나간 시점을 가지고 최소로 설치할 카메라 대수를 계산할 수 있도록 구현하였다.
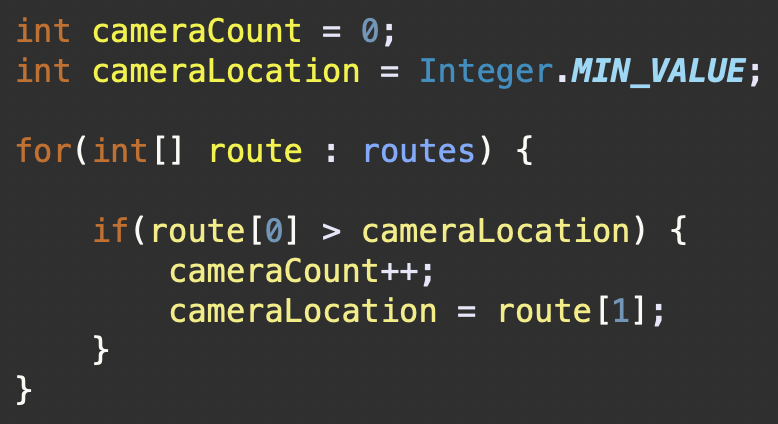
각 차량의 고속도로 진입 지점이 현재 카메라 위치보다 크다는 것은 해당 차량이 아직 단속 카메라를 만나지 않았음을 의미한다. 그래서 새로운 카메라를 설치해야 하며, 이 카메라는 해당 차량의 고속도로 진출 지점에 설치된다. 이렇게 하면 이 차량 뿐만 아니라, 이전에 카메라에 포착되지 않은 다른 차량들도 포착될 수 있는 기회를 최대화 할 수 있다.
베스트앨범
문2) 스트리밍 사이트에서 장르 별로 가장 많이 재생된 노래를 두 개씩 모아 베스트 앨범을 출시하려 합니다. 노래는 고유 번호로 구분하며, 노래를 수록하는 기준은 다음과 같습니다.
- 속한 노래가 많이 재생된 장르를 먼저 수록합니다.
- 장르 내에서 많이 재생된 노래를 먼저 수록합니다.
- 장르 내에서 재생 횟수가 같은 노래 중에서는 고유 번호가 낮은 노래를 먼저 수록합니다.
노래의 장르를 나타내는 문자열 배열 genres와 노래별 재생 횟수를 나타내는 정수 배열 plays가 주어질 때, 베스트 앨범에 들어갈 노래의 고유 번호를 순서대로 return 하도록 solution 함수를 완성하세요.
제한사항
- genres[i]는 고유번호가 i인 노래의 장르입니다.
- plays[i]는 고유번호가 i인 노래가 재생된 횟수입니다.
- genres와 plays의 길이는 같으며, 이는 1 이상 10,000 이하입니다.
- 장르 종류는 100개 미만입니다.
- 장르에 속한 곡이 하나라면, 하나의 곡만 선택합니다.
- 모든 장르는 재생된 횟수가 다릅니다.
입출력 예
| genres | plays | return |
|---|---|---|
["classic", "pop", "classic", "classic", "pop"] | [500, 600, 150, 800, 2500] | [4, 1, 3, 0] |
입출력 예 설명
classic 장르는 1,450회 재생되었으며, classic 노래는 다음과 같습니다.
- 고유 번호 3: 800회 재생
- 고유 번호 0: 500회 재생
- 고유 번호 2: 150회 재생
pop 장르는 3,100회 재생되었으며, pop 노래는 다음과 같습니다.
- 고유 번호 4: 2,500회 재생
- 고유 번호 1: 600회 재생
따라서 pop 장르의 [4, 1]번 노래를 먼저, classic 장르의 [3, 0]번 노래를 그다음에 수록합니다.
- 장르 별로 가장 많이 재생된 노래를 최대 두 개까지 모아 베스트 앨범을 출시하므로 2번 노래는 수록되지 않습니다.
나의 풀이
package programmers;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class BestAlbum {
public static int[] solution(String[] genres, int[] plays) {
Map<String, Integer> genrePlayCount = new HashMap<>();
Map<String, List<int[]>> genreSongs = new HashMap<>();
for (int i = 0; i < genres.length; i++) {
genrePlayCount.put(genres[i], genrePlayCount.getOrDefault(genres[i], 0) + plays[i]);
genreSongs.computeIfAbsent(genres[i], k -> new ArrayList<>()).add(new int[] {i, plays[i]});
}
List<String> sortedGenres = new ArrayList<>(genrePlayCount.keySet());
sortedGenres.sort((a, b) -> genrePlayCount.get(b).compareTo(genrePlayCount.get(a)));
List<Integer> bestAlbum = new ArrayList<>();
for (String genre : sortedGenres) {
List<int[]> songs = genreSongs.get(genre);
songs.sort((a, b) -> b[1] != a[1] ? b[1] - a[1] : a[0] - b[0]); // 재생 횟수 내림차순, 고유 번호 오름차순 정렬
for (int i = 0; i < Math.min(songs.size(), 2); i++) {
bestAlbum.add(songs.get(i)[0]);
}
}
return bestAlbum.stream().mapToInt(i -> i).toArray();
}
public static void main(String[] args) {
String[] genres = {"classic", "pop", "classic", "classic", "pop"};
int[] plays = {500, 600, 150, 800, 2500};
solution(genres, plays);
}
}
가장 먼 노드
문3) n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 노드의 개수 n은 2 이상 20,000 이하입니다.
- 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
- vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
입출력 예
| n | vertex | return |
|---|---|---|
| 6 | [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] | 3 |
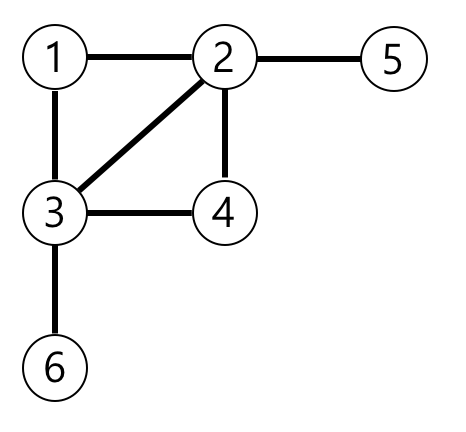
입출력 예 설명
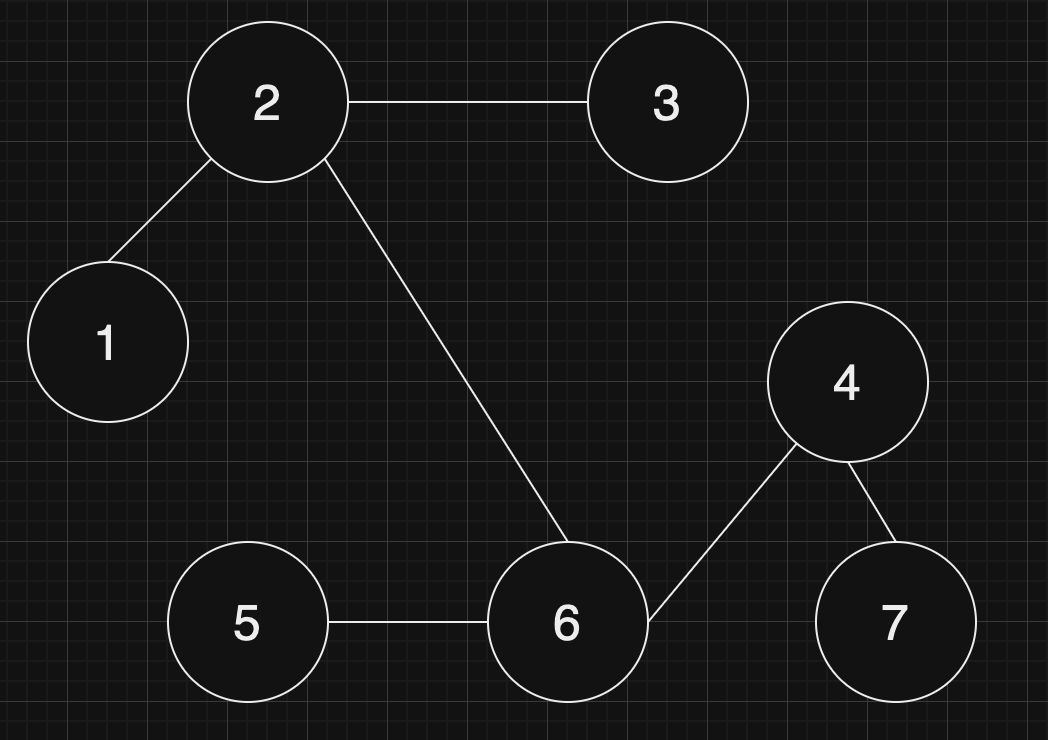
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.
나의 풀이
ArrayList를 활용한 BFS탐색 알고리즘
package programmers;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class FurthestNode {
static ArrayList<Integer>[] graph;
static boolean[] visited;
static int[] distance;
public static void bfs(int start) {
Queue<Integer> q = new LinkedList<>();
q.add(start);
visited[start] = true;
distance[start] = 0;
while(!q.isEmpty()) {
int currrent = q.poll();
for(int next : graph[currrent]) {
if(!visited[next]) {
q.add(next);
visited[next] = true;
distance[next] = distance[currrent] + 1;
}
}
}
}
public static int solution(int n, int[][] edge) {
graph = new ArrayList[n+1];
for(int i = 0; i <= n; i++) {
graph[i] = new ArrayList<>();
}
visited = new boolean[n+1];
distance = new int[n+1];
for (int[] link : edge) {
int x = link[0];
int y = link[1];
graph[x].add(y);
graph[y].add(x);
}
bfs(1);
int maxDistance = 0;
for(int i = 1; i <= n; i++) {
if(distance[i] > maxDistance) {
maxDistance = distance[i];
}
}
int count = 0;
for(int i = 0; i <= n; i++) {
if(distance[i] == maxDistance) {
count++;
}
}
return count;
}
public static void main(String[] args) {
int[][] edge = {{3, 6}, {4, 3}, {3, 2}, {1, 3}, {1, 2}, {2, 4}, {5, 2}};
solution(6, edge);
}
}
HashMap을 활용한 BFS탐색 알고리즘
package programmers;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;
public class FurthestNode {
static Map<Integer, List<Integer>> graph;
static boolean[] visited;
static int[] distance;
public static void bfs(int start) {
Queue<Integer> q = new LinkedList<>();
q.add(start);
visited[start] = true;
distance[start] = 0;
while(!q.isEmpty()) {
int currrent = q.poll();
for(int next : graph.get(currrent)) {
System.out.println(next);
if(!visited[next]) {
q.add(next);
visited[next] = true;
distance[next] = distance[currrent] + 1;
}
}
}
}
public static int solution(int n, int[][] edge) {
graph = new HashMap<>();
for (int[] link : edge) {
int x = link[0];
int y = link[1];
graph.computeIfAbsent(x, k -> new ArrayList<>()).add(y);
graph.computeIfAbsent(y, k -> new ArrayList<>()).add(x);
}
visited = new boolean[n+1];
distance = new int[n+1];
bfs(1);
int maxDistance = 0;
for(int i = 1; i <= n; i++) {
if(distance[i] > maxDistance) {
maxDistance = distance[i];
}
}
int count = 0;
for(int i = 0; i <= n; i++) {
if(distance[i] == maxDistance) {
count++;
}
}
System.out.println(count);
return count;
}
public static void main(String[] args) {
int[][] edge = {{3, 6}, {4, 3}, {3, 2}, {1, 3}, {1, 2}, {2, 4}, {5, 2}};
solution(6, edge);
}
}
나의 생각
DFS 말고 BFS 알고리즘을 선택한 근거
1. 최단 경로 문제 : 문제에서 요구하는 것은 1번 node로부터
가장 멀리 떨어진 노드, 즉 최단 경로로 이동했을 때
간선의 개수가 가장 많은 노드들이다.
👉🏻 BFS는 그래프에서 깊이(depth)별로 탐색을 진행하기 때문에 최단 경로를 찾는데 적합
2. 동일한 거리에 있는 모든 node 탐색 : BFS는 시작 노드로부터의 거리가
동일한 모든 노드들을 같은 깊이(depth)에서 탐색. 이 특성은 모든 간선의 가중치가
동일할 때(이 경우에는 1), 가장 멀리 떨어진 노드들을 찾는데 효과적임
3. 간선의 가중치 일정 : 주어진 문제에서 모든 간선의 가중치는 같고
단순히 연결된 노드 간의 관계만을 나타냄.
👉🏻 이는 BFS가 특히 적합한 환경
💡 DFS는 경로의 가능성을 추적할 때 유용하지만, 최단 경로 문제에는 BFS가
더 적합한 알고리즘이다. DFS를 사용하면 가장 멀리 떨어진 노드에 도달하는
경로를 찾을 수 있지만, 그것이 최단 경로인지는 보장할 수 없고, 같은 거리에
있는 모든 노드를 찾는 것도 비효율적이다.섬 연결하기
문4) n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
입출력 예
| n | costs | return |
|---|---|---|
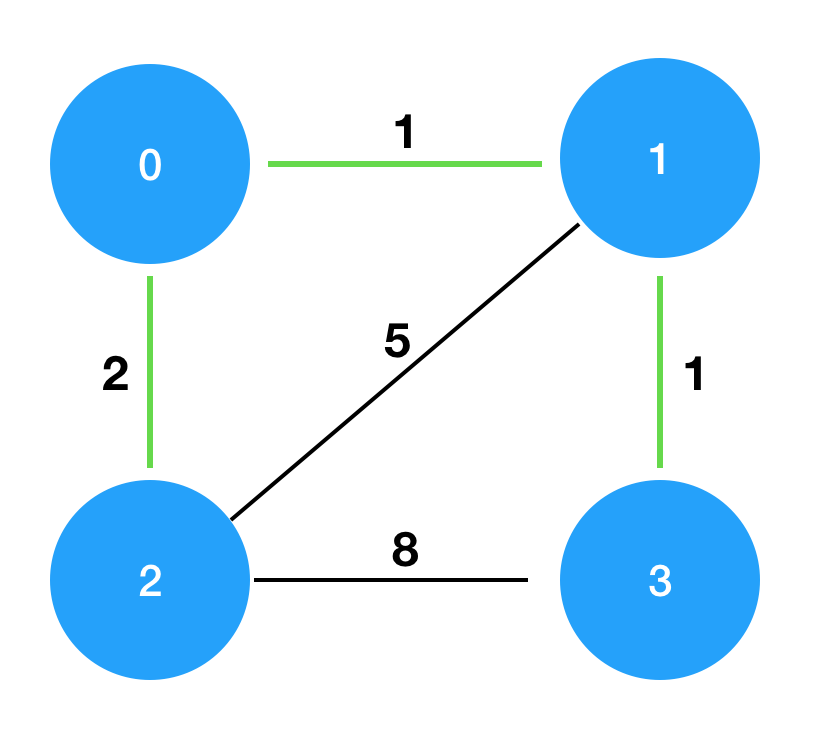
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
입출력 예 설명
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
나의 풀이
package programmers;
import java.util.Arrays;
import java.util.Comparator;
public class IslandConnection {
static int[] parent;
// Union - Find 알고리즘의 find 함수
public static int find(int node) {
if(parent[node] == node) {
return node;
}
return parent[node] = find(parent[node]);
}
// Union - Find 알고리즘의 union 함수
public static void union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if(rootA != rootB) {
parent[rootB] = rootA;
}
}
public static int solution(int n, int[][] costs) {
int answer = 0;
parent = new int[n];
for(int i = 0; i < n; i++) {
parent[i] = i;
}
Arrays.sort(costs, Comparator.comparingInt(o -> o[2]));
for(int[] cost : costs) {
System.out.println(Arrays.toString(cost));
}
// 간선들을 순회하면서 두 섬을 연결
for(int[] cost : costs) {
int a = find(cost[0]);
int b = find(cost[1]);
System.out.printf("a: %d, b: %d\n",a,b);
if(a != b) {
union(a,b);
answer += cost[2];
}
}
return answer;
}
public static void main(String[] args) {
int[][] costs = {{0,1,1},{0,2,2},{1,2,5},{1,3,1},{2,3,8}};
solution(4, costs);
}
}
나의 생각
연결 그래프를 만드는데 필요한 최소 비용을 찾는 최소 신장 트리(Minimum Spanning Tree, MST)
- 그래프에서 모든 노드(Node)를 포함하면서 사이클이 존재하지 않는 부분 그래프
신장 트리 예시
탐욕법(Greedy Algorithm) - 크루스칼(Kruskal)알고리즘- 간선을 가중치의 오름차순으로 정렬한 후, 사이클을 형성하지 않는 선에서 간선을 선택해 최소 신장 트리를 만드는 방법
로직 구현 방법
1. 모든 간선을 가중치에 따라 오름차순으로 정렬
2. 각 섬을 독립적인 집합으로 초기화
3. 정렬된 간선 리스트를 순회하면서 다음을 수행
- 간선이 연결하는 두 섬이 이미 같은 집합에 속해 있지 않다면,
(즉, 사이클을 형성하지 않는다면,) 이 간선을 선택하고 두 섬을 같은 집합으로 합침
- 선택된 간선의 가중치를 결과에 더함
4. 모든 섬이 연결될 때까지 3번을 반복
5. 최종 결과를 반환여행경로
문5) 주어진 항공권을 모두 이용하여 여행경로를 짜려고 합니다. 항상 "ICN" 공항에서 출발합니다.
항공권 정보가 담긴 2차원 배열 tickets가 매개변수로 주어질 때, 방문하는 공항 경로를 배열에 담아 return 하도록 solution 함수를 작성해주세요.
제한사항
- 모든 공항은 알파벳 대문자 3글자로 이루어집니다.
- 주어진 공항 수는 3개 이상 10,000개 이하입니다.
- tickets의 각 행 [a, b]는 a 공항에서 b 공항으로 가는 항공권이 있다는 의미입니다.
- 주어진 항공권은 모두 사용해야 합니다.
- 만일 가능한 경로가 2개 이상일 경우 알파벳 순서가 앞서는 경로를 return 합니다.
- 모든 도시를 방문할 수 없는 경우는 주어지지 않습니다.
입출력 예
| tickets | return |
|---|---|
[["ICN", "JFK"], ["HND", "IAD"], ["JFK", "HND"]] | ["ICN", "JFK", "HND", "IAD"] |
[["ICN", "SFO"], ["ICN", "ATL"], ["SFO", "ATL"], ["ATL", "ICN"], ["ATL","SFO"]] | ["ICN", "ATL", "ICN", "SFO", "ATL", "SFO"] |
입출력 예 설명
예제 #1
- ["ICN", "JFK", "HND", "IAD"] 순으로 방문할 수 있습니다.
예제 #2
- ["ICN", "SFO", "ATL", "ICN", "ATL", "SFO"] 순으로 방문할 수도 있지만 ["ICN", "ATL", "ICN", "SFO", "ATL", "SFO"] 가 알파벳 순으로 앞섭니다.
나의 풀이
package programmers;
import java.util.Arrays;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public class TravelRoute {
static boolean[] visited;
static List<String> answerList;
public static void dfs(String[][] tickets, String current, LinkedList<String> route) {
if (route.size() == tickets.length + 1) {
answerList = new LinkedList<>(route);
return;
}
for(int i = 0; i < tickets.length; i++) {
if(!visited[i] && tickets[i][0].equals(current)) {
visited[i] = true;
route.add(tickets[i][1]);
dfs(tickets, tickets[i][1], route);
if (answerList != null) return;
route.removeLast();
visited[i] = false;
}
}
}
public static String[] solution(String[][] tickets) {
visited = new boolean[tickets.length];
Arrays.sort(tickets, Comparator.comparing((String[] ticket) -> ticket[0]).thenComparing(ticket -> ticket[1]));
LinkedList<String> route = new LinkedList<>();
route.add("ICN");
dfs(tickets, "ICN", route);
return answerList.toArray(new String[0]);
}
public static void main(String[] args) {
String[][] tickets = {{"ICN", "SFO"},
{"ICN", "ATL"},
{"SFO", "ATL"},
{"ATL", "ICN"},
{"ATL", "SFO"}};
solution(tickets);
}
}
나의 생각
이 문제를 DFS로 풀어야겠다고 생각한 문제의 힌트는 다음과 같다.
1. 모든 항공권 사용 : 문제에서 모든 항공권을 사용해야 한다고 명시
이는 경로를 찾는 과정에서 선택지를 한 번씩만 사용하고, 모든 선택지를
사용해야 한다는 것을 의미
👉🏻 가능한 경로를 탐색한다는 점에서 DFS 알고리즘 선택이 유리
2. 알파벳 순서 : 가능한 경로가 여러 개일 경우 알파벳 순서가 앞서는 경로를
선택해야 한다는 요구사항이 있음.
이는 DFS를 사용하여 모든 경로를 탐색하고, 탐색 과정에서 알파벳 순으로
경로를 정렬할 필요가 있음을 시사
3. 시작 공항 : 모든 여행 경로가 "ICN"공항에서 시작한다는 점은 탐색의
시작점이 고정되어 있음을 의미
👉🏻 DFS는 시작점으로부터 시작하여 모든 경로를 탐색할 수 있음
4. 공항 수의 범위 : 주어진 공항 수가 최대 10,000개로 많지 않다는 점은
완전 탐색 알고리즘인 DFS를 사용해도 처리 가능한 범위라는 것을 암시
5. 방문할 수 없는 경우의 배제 : 모든 도시를 방문할 수 없는 경우는 없다고 명시
👉🏻 이는 탐색 과정에서 끝까지 탐색이 가능하다는 것을 보장로직은 어떻게 구현할 것인가?
- 이미 방문한 경로를 재방문 하지 않도록 하여 가능한 경로를 탐색할 수 있게 하는
boolean[] visited 배열 선언


tickets배열을 어떻게 알파셋 순서로 정렬할 것인가?

- 위 코드는 두 단계의 기준을 사용하여 배열을 정렬한다.
- 첫번째 기준 :
Comparator.comparing((String[] ticket) -> ticket[0])은 항공권 배열의 첫 번째 요소(출발 공항)를 알파벳 순으로 정렬
- 두 번째 기준 :
thenComparing(ticket -> ticket[1])은 첫 번째 기준으로 비교한 결과가 동일할 때 (즉, 같은 출발 공항을 가지는 경우) 도착 공항을 기준으로 추가 정렬을 수행함
👉🏻thenComparing메서드는 첫 번째 기준의 비교 결과가 같은 경우에만 사용됨
| 원래 순서 | 정렬된 순서 |
|---|---|
 |  |
- 여행 출발지 , 경유지 및 목적지를 넣을
LinkedList를 생성

흔히 사용되는 ArrayList도 있는데 생소한 LinkedList를 쓴 이유는 무엇인가?
1. LinkedList의 선택 이유 :
- DFS 알고리즘에서 경로 추적과 백트래킹을 위해 빈번한 요소 추가 및 삭제가 필요
- LinkedList는 이러한 작업에 적합한 자료구조
- LinkedList는 스택 및 큐의 동작을 모방할 수 있는 DEQUE 인터페이스를 구현함
- addLast와 removeLast 메서드를 통해 스택의 동작을 자연스럽게 지원
- 문제의 크기가 크지 않아 LinkedList의 추가적인 메모리 사용이 큰 부담이 되지 않으며,
요소 접근이 주로 리스트의 끝에서 이루어지므로 LinkedList의 성능이 효율적임
2. LIFO(Last In First Out) 원칙 :
- DFS 알고리즘은 스택의 LIFO 원칙을 따름. 즉, 가장 최근에 삽입된 요소가
가장 먼저 나오는 구조
- 현재 경로에서 가능한 한 깊게 탐색을 진행한 후, 더 이상 탐색할 수 없을 때
이전 단계로 돌아가는 방식으로 탐색함. 이는 마지막으로 방문한 노드부터
차례로 되돌아가는 스택의 동작과 일치
3. addLast와 removeLast 메서드의 역할 :
- addLast 메서드는 LinkedList의 끝에 새로운 요소를 추가하여
스택의 push 동작을 모방함
- removeLast 메서드는 LinkedList의 마지막 요소를 제거하고 반환하여
스택의 pop 동작을 모방함 ArrayList와 LinkedList의 특징 및 차이점
| 특징/차이점 | ArrayList | LinkedList |
|---|---|---|
| 내부 구조 | 동적 배열 | 이중 연결 리스트 |
| 요소 추가/삭제 | 끝에서는 빠름, 중간은 느림 (배열 재구성 필요) | 어디에서나 빠름 (노드의 링크 변경) |
| 메모리 사용 | 요소만큼의 메모리 사용 (최소화) | 각 요소가 노드의 이전/다음 포인터 추가 메모리 사용 |
| 요소 접근 | 인덱스를 통한 빠른 임의 접근 (O(1)) | 선형 접근, 시작/끝은 빠르지만 중간은 느림 (O(n)) |
| 스택/큐 용도 | 가능하지만 비효율적 | addLast, removeLast 메소드로 스택/큐 구현에 적합 |
| Backtracking | 가능하지만 remove 시 시간 복잡도에 주의 | 요소 추가 및 제거가 상수 시간이므로 backtracking에 유리 |
| 성능 | 크기 변경이 적고, 랜덤 액세스가 많은 경우 선호 | 요소의 추가/삭제가 빈번하고 크기 변경이 잦은 경우 선호 |
- dfs 메서드 구현
static List<String> answerList; // 최종 여행 경로를 저장하는 리스트
public static void dfs(String[][] tickets, String current, LinkedList<String> route){
// 현재 경로의 길이가 항공권 수 + 1과 같으면 모든 항공권을 사용한 것임
if (route.size() == tickets.length + 1) {
answerList = new LinkedList<>(route); // 최종 경로를 answerList에 저장
return; // 추가 탐색 중단
}
// 모든 항공권을 순회
for(int i = 0; i < tickets.length; i++){
// 아직 사용하지 않은 항공권이고, 현재 공항에서 출발하는 항공권인 경우
if(!visited[i] && tickets[i][0].equals(current)){
visited[i] = true; // 해당 항공권을 사용한 것으로 표시
route.add(tickets[i][1]; // 경로에 다음 목적지 추가
dfs(tickets, tickets[i][1], route); // 다음 목적지에서 DFS 계속 진행
if (answerList != null) return; // 이미 답을 찾았으면 추가 탐색 중단
route.removeLast(); // 현재 선택한 항공권이 유효한 경로가 아니면 제거 (백트래킹)
visited[i] = false; // 항공권 사용 취소
}
}
}