요격 시스템
문1) A 나라가 B 나라를 침공하였습니다. B 나라의 대부분의 전략 자원은 아이기스 군사 기지에 집중되어 있기 때문에 A 나라는 B 나라의 아이기스 군사 기지에 융단폭격을 가했습니다.
A 나라의 공격에 대항하여 아이기스 군사 기지에서는 무수히 쏟아지는 폭격 미사일들을 요격하려고 합니다. 이곳에는 백발백중을 자랑하는 요격 시스템이 있지만 운용 비용이 상당하기 때문에 미사일을 최소로 사용해서 모든 폭격 미사일을 요격하려 합니다.
A 나라와 B 나라가 싸우고 있는 이 세계는 2 차원 공간으로 이루어져 있습니다. A 나라가 발사한 폭격 미사일은 x 축에 평행한 직선 형태의 모양이며 개구간을 나타내는 정수 쌍 (s, e) 형태로 표현됩니다. B 나라는 특정 x 좌표에서 y 축에 수평이 되도록 미사일을 발사하며, 발사된 미사일은 해당 x 좌표에 걸쳐있는 모든 폭격 미사일을 관통하여 한 번에 요격할 수 있습니다. 단, 개구간 (s, e)로 표현되는 폭격 미사일은 s와 e에서 발사하는 요격 미사일로는 요격할 수 없습니다. 요격 미사일은 실수인 x 좌표에서도 발사할 수 있습니다.
각 폭격 미사일의 x 좌표 범위 목록 targets이 매개변수로 주어질 때, 모든 폭격 미사일을 요격하기 위해 필요한 요격 미사일 수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
제한 사항
- 1 ≤ targets의 길이 ≤ 500,000
- targets의 각 행은 [s,e] 형태입니다.
- 이는 한 폭격 미사일의 x 좌표 범위를 나타내며, 개구간 (s, e)에서 요격해야 합니다.
- 0 ≤ s < e ≤ 100,000,000
입출력 예
| targets | result |
|---|---|
[[4,5],[4,8],[10,14],[11,13],[5,12],[3,7],[1,4]] | 3 |
입출력 예 설명
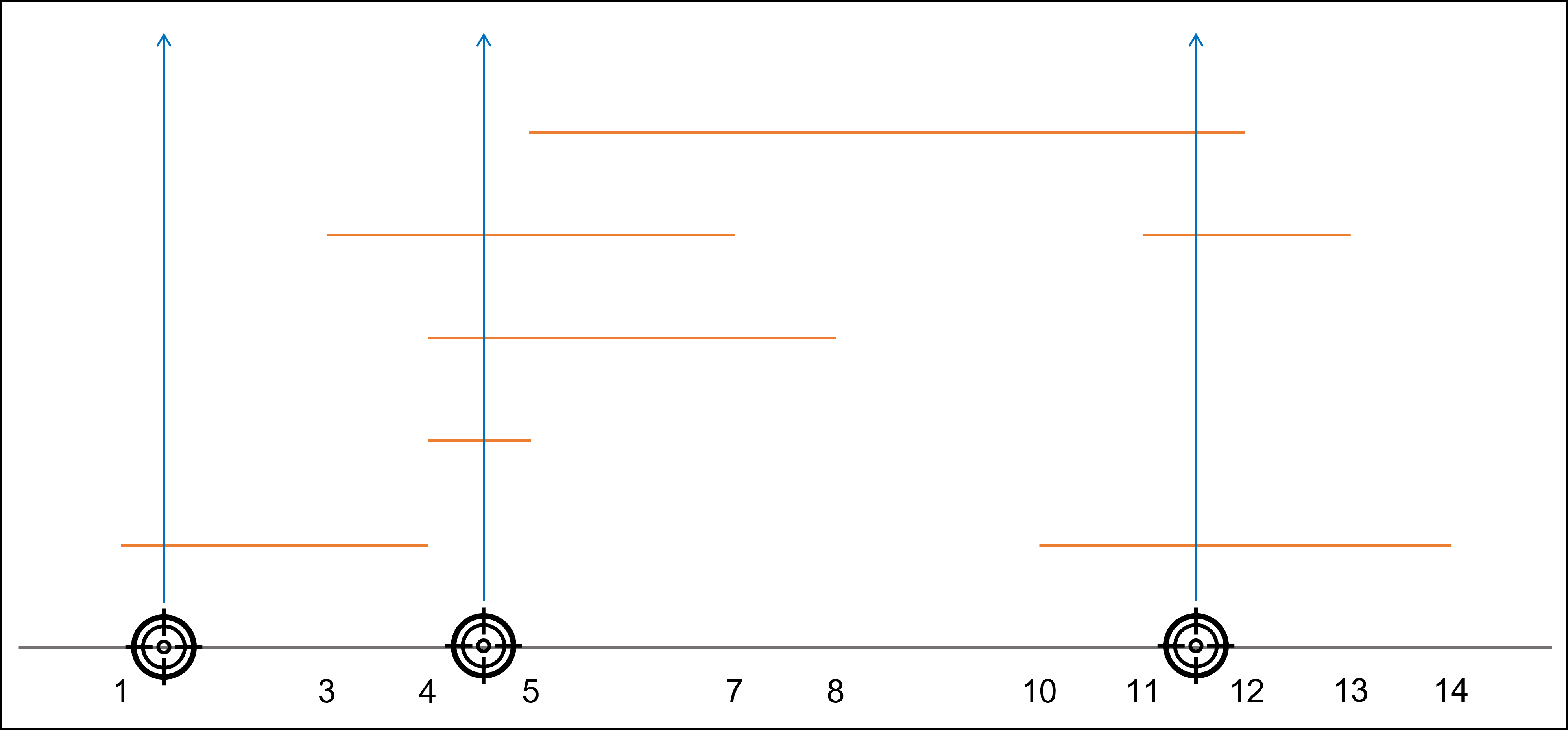
위 그림과 같이 최소 세 번의 요격 미사일 발사로 전부 방어할 수 있습니다.
나의 풀이
package programmers;
import java.util.Arrays;
import java.util.Comparator;
public class InterceptionSystem {
public static int solution(int[][] targets) {
Arrays.sort(targets, Comparator.comparingInt(o -> o[1]));
int missileCount = 0;
double lastIntercept = -0.5;
for(int[] target : targets) {
if(target[0] > lastIntercept) {
missileCount++;
System.out.println(target[1]);
lastIntercept = target[1] - 0.1;
}
}
return missileCount;
}
public static void main(String[] args) {
int[][] targets = {{4,5},{4,8},{10,14},{11,13},{5,12},{3,7},{1,4}};
solution(targets);
}
}
나의 생각
탐욕(Greedy)법
내가 이번 문제를 탐욕법으로 풀어야겠다고 생각한 문제의 hint는 다음과 같다
1. 구간 커버링 문제 : 문제의 핵심은 여러 개의 폭격 미사일 구간을
최소한의 요격 미사일로 커버하는것
2. 개구간 요격의 제약 : 각 폭격 미사일 구간은 개구간 `(s,e)`로 표현되며
s,e점에서 요격할 수 없다는 제약으로 이는 구간의 끝점에서 가장 가까운 실수 좌표에서
요격 미사일을 발사하여 여러 구간을 동시에 커버할 수 있는 최적의 선택을 해야함
3. 최소 요격 미사일 수 : 문제에서 요구하는 것은 모든 폭격 미사일을 요격하는 것이 아니라
그렇게 하기 위해 필요한 최소한의 요격 미사일 수이다.
그리디 알고리즘은 이러한 최소화 또는 최대화 문제에 자주 사용되며
각 단계에서 최적의 선택을 하여 전체적으로 최적의 결과를 도출함
4. 끝점을 기준으로 한 정렬 : 문제 해결을 위해 구간들을 끝점을 기준으로 정렬하는 방법은
그리디 알고리즘에서 자주 사용되는 패턴이다.내가 했던 실수
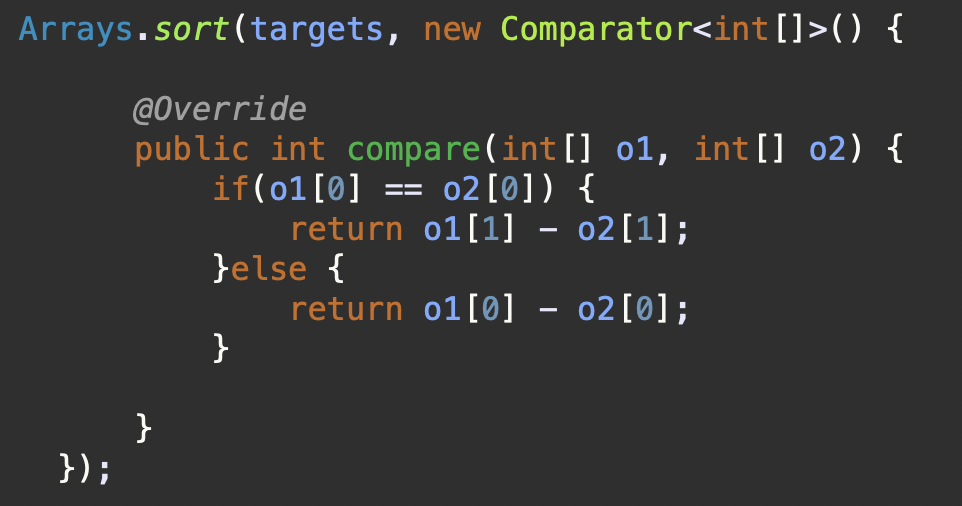
s(start)점 기준 정렬 후 e(end) 점 정렬 (❌) - > e(end) 점만 정렬 (⭕️)
| s점 기준 정렬 후 e점 정렬 | e점을 기준으로 정렬 |
|---|---|
 |  |
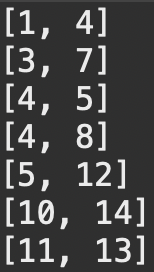 | 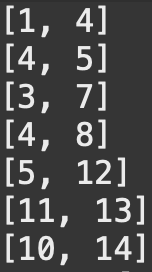 |
| s점 기준 정렬 후 e점 정렬은 끝점의 최소화라는 관점에서 최적의 해를 항상 보장하지 않음(겹치는 구간을 놓칠 수 있음) | 끝점이 가장 작은 구간부터 처리하게 되며, 한 요격 미사일로 커버할 수 있는 최대한의 구간을 커버할 수 있음 |
int missileCount = 0;
double lastIntercept = -0.5; // -0.5는 시작 전의 임의의 값
for(int[] target : targets) {
// 현재 구간의 시작점이 마지막 요격 지점보다 크면 요격 미사일을 발사
if(target[0] > lastIntercept) {
missileCount++;
// 0.1을 빼는 이유는 끝점 자체는 요격할 수 없으므로, 끝점 바로 앞 실수점을 요격
lastIntercept = target[1] - 0.1;
}
}양궁대회
문2) 카카오배 양궁대회가 열렸습니다.
라이언은 저번 카카오배 양궁대회 우승자이고 이번 대회에도 결승전까지 올라왔습니다. 결승전 상대는 어피치입니다.
카카오배 양궁대회 운영위원회는 한 선수의 연속 우승보다는 다양한 선수들이 양궁대회에서 우승하기를 원합니다. 따라서, 양궁대회 운영위원회는 결승전 규칙을 전 대회 우승자인 라이언에게 불리하게 다음과 같이 정했습니다.
- 어피치가 화살 n발을 다 쏜 후에 라이언이 화살 n발을 쏩니다.
- 점수를 계산합니다.
-
과녁판은 아래 사진처럼 생겼으며 가장 작은 원의 과녁 점수는 10점이고 가장 큰 원의 바깥쪽은 과녁 점수가 0점입니다.

-
-
만약, k(k는 1~10사이의 자연수)점을 어피치가 a발을 맞혔고 라이언이 b발을 맞혔을 경우 더 많은 화살을 k점에 맞힌 선수가 k 점을 가져갑니다. 단, a = b일 경우는 어피치가 k점을 가져갑니다. k점을 여러 발 맞혀도 k점 보다 많은 점수를 가져가는 게 아니고 k점만 가져가는 것을 유의하세요. 또한 a = b = 0 인 경우, 즉, 라이언과 어피치 모두 k점에 단 하나의 화살도 맞히지 못한 경우는 어느 누구도 k점을 가져가지 않습니다.
- 예를 들어, 어피치가 10점을 2발 맞혔고 라이언도 10점을 2발 맞혔을 경우 어피치가 10점을 가져갑니다.
- 다른 예로, 어피치가 10점을 0발 맞혔고 라이언이 10점을 2발 맞혔을 경우 라이언이 10점을 가져갑니다.
-
모든 과녁 점수에 대하여 각 선수의 최종 점수를 계산합니다.
- 최종 점수가 더 높은 선수를 우승자로 결정합니다. 단, 최종 점수가 같을 경우 어피치를 우승자로 결정합니다.
현재 상황은 어피치가 화살 n발을 다 쏜 후이고 라이언이 화살을 쏠 차례입니다.
라이언은 어피치를 가장 큰 점수 차이로 이기기 위해서 n발의 화살을 어떤 과녁 점수에 맞혀야 하는지를 구하려고 합니다.
화살의 개수를 담은 자연수 n, 어피치가 맞힌 과녁 점수의 개수를 10점부터 0점까지 순서대로 담은 정수 배열 info가 매개변수로 주어집니다. 이때, 라이언이 가장 큰 점수 차이로 우승하기 위해 n발의 화살을 어떤 과녁 점수에 맞혀야 하는지를 10점부터 0점까지 순서대로 정수 배열에 담아 return 하도록 solution 함수를 완성해 주세요. 만약, 라이언이 우승할 수 없는 경우(무조건 지거나 비기는 경우)는 [-1]을 return 해주세요.
제한사항
-
1 ≤ n ≤ 10
-
info의 길이 = 11
- 0 ≤ info의 원소 ≤ n
- info의 원소 총합 = n
- info의 i번째 원소는 과녁의 10 - i 점을 맞힌 화살 개수입니다. ( i는 0~10 사이의 정수입니다.)
-
라이언이 우승할 방법이 있는 경우, return 할 정수 배열의 길이는 11입니다.
-
0 ≤ return할 정수 배열의 원소 ≤ n
-
return할 정수 배열의 원소 총합 = n (꼭 n발을 다 쏴야 합니다.)
-
return할 정수 배열의 i번째 원소는 과녁의 10 - i 점을 맞힌 화살 개수입니다. ( i는 0~10 사이의 정수입니다.)
-
라이언이 가장 큰 점수 차이로 우승할 수 있는 방법이 여러 가지 일 경우, 가장 낮은 점수를 더 많이 맞힌 경우를 return 해주세요.
- 가장 낮은 점수를 맞힌 개수가 같을 경우 계속해서 그다음으로 낮은 점수를 더 많이 맞힌 경우를 return 해주세요.
- 예를 들어, [2,3,1,0,0,0,0,1,3,0,0]과 [2,1,0,2,0,0,0,2,3,0,0]를 비교하면 [2,1,0,2,0,0,0,2,3,0,0]를 return 해야 합니다.
- 다른 예로, [0,0,2,3,4,1,0,0,0,0,0]과 [9,0,0,0,0,0,0,0,1,0,0]를 비교하면[9,0,0,0,0,0,0,0,1,0,0]를 return 해야 합니다.
-
-
라이언이 우승할 방법이 없는 경우, return 할 정수 배열의 길이는 1입니다.
- 라이언이 어떻게 화살을 쏘든 라이언의 점수가 어피치의 점수보다 낮거나 같으면 [-1]을 return 해야 합니다.
입출력 예
| n | info | result |
|---|---|---|
| 5 | [2,1,1,1,0,0,0,0,0,0,0] | [0,2,2,0,1,0,0,0,0,0,0] |
| 1 | [1,0,0,0,0,0,0,0,0,0,0] | [-1] |
| 9 | [0,0,1,2,0,1,1,1,1,1,1] | [1,1,2,0,1,2,2,0,0,0,0] |
| 10 | [0,0,0,0,0,0,0,0,3,4,3] | [1,1,1,1,1,1,1,1,0,0,2] |
입출력 예 설명
입출력 예 #1
- 어피치와 라인어이 아래와 같이 화살을 맞힐 경우
| 과녁점수 | 어피치가 맞힌 화살 개수 | 라이언이 맞힌 화살 개수 | 결과 |
|---|---|---|---|
| 10 | 2 | 3 | 라이언 10점 획득 |
| 9 | 1 | 2 | 라이언 9점 획득 |
| 8 | 1 | 0 | 어피치 8점 획득 |
| 7 | 1 | 0 | 어피치 7점 획득 |
| 6 | 0 | 0 | |
| 5 | 0 | 0 | |
| 4 | 0 | 0 | |
| 3 | 0 | 0 | |
| 2 | 0 | 0 | |
| 1 | 0 | 0 | |
| 0 | 0 | 0 |
어피치의 최종 점수는 15점, 라이언의 최종 점수는 19점입니다. 4점 차이로 라이언이 우승합니다.
하지만, 라이언이 아래와 같이 화살을 맞힐 경우 더 큰 점수 차로 우승할 수 있습니다.
| 과녁점수 | 어피치가 맞힌 화살 개수 | 라이언이 맞힌 화살 개수 | 결과 |
|---|---|---|---|
| 10 | 2 | 0 | 어피치 10점 획득 |
| 9 | 1 | 2 | 라이언 9점 획득 |
| 8 | 1 | 2 | 라이언 8점 획득 |
| 7 | 1 | 0 | 어피치 7점 획득 |
| 6 | 0 | 1 | 라이언 6점 획득 |
| 5 | 0 | 0 | |
| 4 | 0 | 0 | |
| 3 | 0 | 0 | |
| 2 | 0 | 0 | |
| 1 | 0 | 0 | |
| 0 | 0 | 0 |
나의 풀이
직관적인 로직
package programmers;
import java.util.Arrays;
public class ArcheryCompetition {
static int[] bestRyanList;
static int[] ryanList;
static int MAX = 11;
static int bestScoreDiff = Integer.MIN_VALUE;
public static int[] solution(int n, int[] info) {
ryanList = new int[MAX];
bestRyanList = new int[MAX];
backtracking(0,n,info);
System.out.println(Arrays.toString(bestRyanList));
if(bestScoreDiff <= 0) return new int[] {-1};
else return bestRyanList;
}
public static void backtracking(int depth, int n, int[] info) {
if(depth == n) {
int diff = score(info);
if(diff >= bestScoreDiff) {
bestScoreDiff = diff;
bestRyanList = ryanList.clone();
}
return;
}
for(int i = 0; i < info.length && ryanList[i] <= info[i]; i++) {
ryanList[i] += 1;
backtracking(depth + 1, n, info);
ryanList[i] -=1;
}
}
public static int score(int[] info) {
int apeachScore = 0, ryanScore = 0;
for(int i = 0; i < ryanList.length; i++) {
if(info[i] == 0 && ryanList[i] == 0) continue;
if(info[i] >= ryanList[i]) apeachScore += (10 - i);
else ryanScore += (10 - i);
}
int diff = ryanScore - apeachScore;
if(diff <= 0) return -1;
return diff;
}
public static void main(String[] args) {
int n = 9;
int[] info = {0,0,1,2,0,1,1,1,1,1,1};
solution(n, info);
}
}
좀 더 체계적이고, 효율적인 로직
package programmers;
public class ArcheryCompetition {
static int MAX = 11;
static int[] bestRyanList;
static int bestScoreDiff = 0;
public static void calculateScore(int[] info, int[] ryanList) {
int apeachScore = 0;
int ryanScore = 0;
for(int i = 0; i < MAX; i++) {
if(info[i] == 0 && ryanList[i] == 0) continue;
if(info[i] >= ryanList[i]) apeachScore += (10 - i);
else ryanScore += (10 - i);
}
int scoreDiff = ryanScore - apeachScore;
if(scoreDiff > bestScoreDiff) {
bestScoreDiff = scoreDiff;
bestRyanList = ryanList.clone();
} else if (scoreDiff == bestScoreDiff) {
for(int i = MAX - 1; i >= 0; i--) {
if(bestRyanList[i] != ryanList[i]) {
if(ryanList[i] > bestRyanList[i]) {
bestRyanList = ryanList.clone();
}
break;
}
}
}
}
public static void search(int n , int[] info, int[] ryanList, int index) {
if(n < 0) return; // 남은 화살이 없다면 더 이상 진행할 수 없음
if(index == MAX) { // 모든 점대를 고려했다면,
ryanList[MAX - 1] += n; // 남은 모든 화살을 가장 낮은 점수대에 할당
calculateScore(info, ryanList); // 점수를 계산
ryanList[MAX - 1] -= n; // 백트래킹
return;
}
search(n, info, ryanList, index +1); // 현재 점수대에 화살을 쏘지않고 다음 점수대 고려
if(n > info[index]) { // 현재 점수대에 어피치보다 하나 더 많은 화살을 쏠 수 있다
ryanList[index] = info[index] + 1; // 현재 점수대에 화살을 할당
search(n - ryanList[index], info, ryanList, index + 1); // 할당 후 남은 화살로 다음 점수대를 고려
ryanList[index] = 0; // 백트래킹
}
}
public static int[] solution(int n, int[] info) {
bestRyanList = new int[MAX];
bestScoreDiff = 0;
int[] ryanList = new int[MAX];
search(n, info, ryanList, 0);
if(bestScoreDiff == 0) return new int[] {-1};
else return bestRyanList;
}
public static void main(String[] args) {
int n = 9;
int[] info = {0,0,1,2,0,1,1,1,1,1,1};
solution(n, info);
}
}
나의 생각
완점탐색을 깊이(depth)로 수행하느냐, 점수대(index)를 기준으로 수행하느냐에 따라 로직이 다르지만, 각각의 점수대에 대한 명확한 탐색을 위하여 점수대(index)를 기준으로 완전탐색을 수행하였다.
다음 표는 깊이와 점수대의 탐색 방식과 탐색범위의 차이를 나타내었다.
| 기준 | 깊이(depth)를 기준으로 하는 완전탐색 | 점수대(index)를 기준으로 하는 완전탐색 |
|---|---|---|
| 정의 | 화살을 쏜 횟수를 나타냄 | 현재 고려하고 있는 점수대를 나타냄 |
| 재귀 호출 | depth를 하나씩 증가시키며, n 화살을 모두 쏠 때까지 탐색 | 다음 점수대로 이동하며, 각 점수대에서 화살을 쏠 수 있는 모든 경우 고려 |
| 초점 | 화살을 쏘는 순서 | 각 점수대별 가능한 모든 화살 조합 |
| 점수대 정의 | 각 단계에서 화살이 쏘아지는 점수대가 명확하지 않음 | 각 단계에서 화살이 쏘아지는 점수대가 명확함 |
| 탐색 과정 | 덜 체계적이며, 모든 가능한 화살의 조합을 고려함 | 체계적이며, 각 점수대별로 가능한 조합을 정확하게 탐색 |
| 효율성 | 탐색 범위가 넓어질 수 있음 | 효율적이며, 구조적인 탐색 제공 |
특히, 재귀호출을 통한 백트래킹은 이해하기 어려울 수 있는 부분이라, 나 역시 이 부분이 미흡하다고 생각하며, search 메서드를 보면서 내용을 정리 해보고자 한다.
백트래킹이란?
- 각 단계에서 특정 선택을 해보고, 그 선택이 최적의 결과를 가져오지 않으면 이전 상태로 되돌아가 다른 선택을 시도하는 기법
public static void search(int n , int[] info, int[] ryanList, int index) {
if(n < 0) return; // 남은 화살이 없다면 더 이상 진행할 수 없음
if(index == MAX) { // 모든 점대를 고려했다면,
ryanList[MAX - 1] += n; // 남은 모든 화살을 가장 낮은 점수대에 할당
calculateScore(info, ryanList); // 점수를 계산
ryanList[MAX - 1] -= n; // 백트래킹
return;
}
search(n, info, ryanList, index +1); // 현재 점수대에 화살을 쏘지않고 다음 점수대 고려
if(n > info[index]) { // 현재 점수대에 어피치보다 하나 더 많은 화살을 쏠 수 있다
ryanList[index] = info[index] + 1; // 현재 점수대에 화살을 할당
search(n - ryanList[index], info, ryanList, index + 1); // 할당 후 남은 화살로 다음 점수대를 고려
ryanList[index] = 0; // 백트래킹
}
}1. 각 점수대를 고려할 때의 백트래킹:
- search(n, info, ryanList, index + 1) 호출은 현재 점수대(index)에 화살을 쏘지 않고
다음 점수대로 넘어가는 것을 의미. 즉, 현재 점수대에서 0발을 쏘는 것을 고려하고 다음 단계로 진행
- 이렇게 각 점수대에서 0발을 쏘는 경우를 모두 고려한 후에, 현재 점수대에서 가능한 화살의 할당을 탐색
2. 화살 할당 및 추가 탐색:
- if (n > info[index]) 조건문은 현재 점수대에서 어피치보다 하나 더 많은 화살을 쏠 수 있는지 확인.
- 조건을 만족하면, ryanList[index] = info[index] + 1;을 통해 현재 점수대에 화살을 할당하고,
search(n - ryanList[index], info, ryanList, index + 1);를 호출하여 할당 후 남은 화살로
다음 점수대를 고려.
3. 모든 점수대를 고려했을 때의 백트래킹:
- if (index == MAX) 조건문은 모든 점수대를 고려한 경우를 처리.
이 경우, 남은 모든 화살을 가장 낮은 점수대(0점)에 할당하고 (ryanList[MAX - 1] += n), 점수를 계산한 후
(calculateScore(info, ryanList)), 원래 상태로 되돌림(ryanList[MAX - 1] -= n).
이는 탐색이 마지막 단계에 도달했을 때 모든 화살을 소모한 상태를 반영.
4. 재귀적 탐색과 백트래킹:
- 이 과정을 통해, 각 점수대에서 가능한 모든 화살 조합을 체계적으로 탐색.
각 점수대에서의 선택을 탐색한 후에는 백트래킹을 통해 이전 상태로 되돌리고
(ryanList[index] = 0), 다른 조합을 탐색할 수 있도록 함.
이 백트래킹 로직은 각 점수대별로 가능한 모든 화살의 조합을 체계적으로 탐색하며,
최적의 조합을 찾기 위해 이전 상태로 되돌리는 것이 핵심.
이를 통해 최적의 조합을 찾을 수 있음.
[1, 1, 2, 0, 1, 2, 2, 0, 0, 0, 0] 조합을 얻는 과정
1. 10점 점수대 (index = 0)
- search(9, info, ryanList, 1); 호출로 10점에 화살을 쏘지 않고,
9점으로 넘어감
- 그 다음, ryanList[0] = info[0] + 1 (즉, ryanList[0] = 1)로
10점에 한발을 쏘고, 나머지 8발로 다음 점수대를 고려함
2. 9점 점수대 (index = 1)
- search(8, info, ryanList, 2); 호출로 9점에 화살을 쏘지 않고,
8점으로 넘어감
- 그 다음, ryanList[1] = info[1] + 1 (즉, ryanList[1] = 1)로
9점에 한발을 쏘고, 나머지 7발로 다음 점수대를 고려함
3. 8점 점수대 (index = 2)
- ryanList[2] = info[2] + 1; (즉, ryanList[2] = 2)로 8점에
두발을 쏨
- 그 후 search(5, info, ryanList, 3); 호출로 남은 다섯발로 7점
점수대를 고려함
4. 이후 점수대
- 이 과정을 반복하며, 각 점수대에서 화살을 쏘거나 쏘지 않는 선택을 하며 탐색
5. 마지막 점수대 (index = 10)
- index = MAX에 도달하면, 남은 화살을 모두 0점에 할당 (ryanList[10] += 남은
화살 수)
6. 점수 계산 및 백트래킹:
- calculateScore(info, ryanList)로 점수를 계산하고, ryanList[10] -= 남은
화살 수로 백트래킹을 수행
7. 최적 조합 업데이트
- 탐색 과정에서 얻은 최고 점수가 기존의 최고 점수보다 높다면, bestRyanList를
현재 ryanList로 업데이트순위 검색
문3) 카카오는 하반기 경력 개발자 공개채용을 진행 중에 있으며 현재 지원서 접수와 코딩테스트가 종료되었습니다. 이번 채용에서 지원자는 지원서 작성 시 아래와 같이 4가지 항목을 반드시 선택하도록 하였습니다.
- 코딩테스트 참여 개발언어 항목에 cpp, java, python 중 하나를 선택해야 합니다.
- 지원 직군 항목에 backend와 frontend 중 하나를 선택해야 합니다.
- 지원 경력구분 항목에 junior와 senior 중 하나를 선택해야 합니다.
- 선호하는 소울푸드로 chicken과 pizza 중 하나를 선택해야 합니다.
인재영입팀에 근무하고 있는 니니즈는 코딩테스트 결과를 분석하여 채용에 참여한 개발팀들에 제공하기 위해 지원자들의 지원 조건을 선택하면 해당 조건에 맞는 지원자가 몇 명인 지 쉽게 알 수 있는 도구를 만들고 있습니다.
예를 들어, 개발팀에서 궁금해하는 문의사항은 다음과 같은 형태가 될 수 있습니다.
코딩테스트에 java로 참여했으며, backend 직군을 선택했고, junior 경력이면서, 소울푸드로 pizza를 선택한 사람 중 코딩테스트 점수를 50점 이상 받은 지원자는 몇 명인가?
물론 이 외에도 각 개발팀의 상황에 따라 아래와 같이 다양한 형태의 문의가 있을 수 있습니다.
- 코딩테스트에 python으로 참여했으며, frontend 직군을 선택했고, senior 경력이면서, 소울푸드로 chicken을 선택한 사람 중 코딩테스트 점수를 100점 이상 받은 사람은 모두 몇 명인가?
- 코딩테스트에 cpp로 참여했으며, senior 경력이면서, 소울푸드로 pizza를 선택한 사람 중 코딩테스트 점수를 100점 이상 받은 사람은 모두 몇 명인가?
- backend 직군을 선택했고, senior 경력이면서 코딩테스트 점수를 200점 이상 받은 사람은 모두 몇 명인가?
- 소울푸드로 chicken을 선택한 사람 중 코딩테스트 점수를 250점 이상 받은 사람은 모두 몇 명인가?
- 코딩테스트 점수를 150점 이상 받은 사람은 모두 몇 명인가?
즉, 개발팀에서 궁금해하는 내용은 다음과 같은 형태를 갖습니다.
* [조건]을 만족하는 사람 중 코딩테스트 점수를 X점 이상 받은 사람은 모두 몇 명인가?
문제
지원자가 지원서에 입력한 4가지의 정보와 획득한 코딩테스트 점수를 하나의 문자열로 구성한 값의 배열 info, 개발팀이 궁금해하는 문의조건이 문자열 형태로 담긴 배열 query가 매개변수로 주어질 때,
각 문의조건에 해당하는 사람들의 숫자를 순서대로 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- info 배열의 크기는 1 이상 50,000 이하입니다.
- info 배열 각 원소의 값은 지원자가 지원서에 입력한 4가지 값과 코딩테스트 점수를 합친 "개발언어 직군 경력 소울푸드 점수" 형식입니다.
- 개발언어는 cpp, java, python 중 하나입니다.
- 직군은 backend, frontend 중 하나입니다.
- 경력은 junior, senior 중 하나입니다.
- 소울푸드는 chicken, pizza 중 하나입니다.
- 점수는 코딩테스트 점수를 의미하며, 1 이상 100,000 이하인 자연수입니다.
- 각 단어는 공백문자(스페이스 바) 하나로 구분되어 있습니다.
- query 배열의 크기는 1 이상 100,000 이하입니다.
- query의 각 문자열은 "[조건] X" 형식입니다.
- [조건]은 "개발언어 and 직군 and 경력 and 소울푸드" 형식의 문자열입니다.
- 언어는 cpp, java, python, - 중 하나입니다.
- 직군은 backend, frontend, - 중 하나입니다.
- 경력은 junior, senior, - 중 하나입니다.
- 소울푸드는 chicken, pizza, - 중 하나입니다.
- '-' 표시는 해당 조건을 고려하지 않겠다는 의미입니다.
- X는 코딩테스트 점수를 의미하며 조건을 만족하는 사람 중 X점 이상 받은 사람은 모두 몇 명인 지를 의미합니다.
- 각 단어는 공백문자(스페이스 바) 하나로 구분되어 있습니다.
- 예를 들면, "cpp and - and senior and pizza 500"은 "cpp로 코딩테스트를 봤으며, 경력은 senior 이면서 소울푸드로 pizza를 선택한 지원자 중 코딩테스트 점수를 500점 이상 받은 사람은 모두 몇 명인가?"를 의미합니다.
입출력 예
| info | query | result |
|---|---|---|
["java backend junior pizza 150","python frontend senior chicken 210","python frontend senior chicken 150","cpp backend senior pizza 260","java backend junior chicken 80","python backend senior chicken 50"] | ["java and backend and junior and pizza 100","python and frontend and senior and chicken 200","cpp and - and senior and pizza 250","- and backend and senior and - 150","- and - and - and chicken 100","- and - and - and - 150"] | [1,1,1,1,2,4] |
입출력 예 설명
지원자 정보를 표로 나타내면 다음과 같습니다.
| 언어 | 직군 | 경력 | 소울푸드 | 점수 |
|---|---|---|---|---|
| java | backend | junior | pizza | 150 |
| python | frontend | senior | chicken | 210 |
| python | frontend | senior | chicken | 150 |
| cpp | backend | senior | pizza | 260 |
| java | backend | junior | chicken | 80 |
| python | backend | senior | chicken | 50 |
-
"java and backend and junior and pizza 100": java로 코딩테스트를 봤으며, backend 직군을 선택했고 junior 경력이면서 소울푸드로 pizza를 선택한 지원자 중 코딩테스트 점수를 100점 이상 받은 지원자는 1명 입니다. -
"python and frontend and senior and chicken 200": python으로 코딩테스트를 봤으며, frontend 직군을 선택했고, senior 경력이면서 소울 푸드로 chicken을 선택한 지원자 중 코딩테스트 점수를 200점 이상 받은 지원자는 1명 입니다. -
"cpp and - and senior and pizza 250": cpp로 코딩테스트를 봤으며, senior 경력이면서 소울푸드로 pizza를 선택한 지원자 중 코딩테스트 점수를 250점 이상 받은 지원자는 1명 입니다. -
"- and backend and senior and - 150": backend 직군을 선택했고, senior 경력인 지원자 중 코딩테스트 점수를 150점 이상 받은 지원자는 1명 입니다. -
"- and - and - and chicken 100": 소울푸드로 chicken을 선택한 지원자 중 코딩테스트 점수를 100점 이상을 받은 지원자는 2명 입니다. -
"- and - and - and - 150": 코딩테스트 점수를 150점 이상 받은 지원자는 4명 입니다.
정확성 통과, 효율성 실패 로직
import java.util.ArrayList;
import java.util.List;
public class RankSearch {
static ArrayList<InfoFive> infoList;
public static class InfoFive {
String language;
String field;
String career;
String food;
int score;
public InfoFive(String language, String field, String career, String food, int score) {
this.language = language;
this.field = field;
this.career = career;
this.food = food;
this.score = score;
}
}
public static int[] solution(String[] info, String[] query) {
infoList = new ArrayList<>();
for (String i : info) {
String[] parts = i.split(" ");
InfoFive infoFive = new InfoFive(parts[0], parts[1], parts[2], parts[3], Integer.parseInt(parts[4]));
infoList.add(infoFive);
}
int[] answer = new int[query.length];
for (int i = 0; i < query.length; i++) {
answer[i] = getAnswer(query[i]);
}
return answer;
}
private static int getAnswer(String query) {
String[] parts = query.replace(" and ", " ").split(" ");
String language = parts[0];
String field = parts[1];
String career = parts[2];
String food = parts[3];
int score = Integer.parseInt(parts[4]);
List<InfoFive> filteredList = new ArrayList<>();
for (InfoFive info : infoList) {
if ((language.equals("-") || info.language.equals(language)) &&
(field.equals("-") || info.field.equals(field)) &&
(career.equals("-") || info.career.equals(career)) &&
(food.equals("-") || info.food.equals(food)) &&
info.score >= score) {
filteredList.add(info);
}
}
return filteredList.size();
}
public static void main(String[] args) {
String[] info = {"java backend junior pizza 150", "python frontend senior chicken 210", "python frontend senior chicken 150", "cpp backend senior pizza 260", "java backend junior chicken 80", "python backend senior chicken 50"};
String[] query = {"java and backend and junior and pizza 100", "python and frontend and senior and chicken 200", "cpp and - and senior and pizza 250", "- and backend and senior and - 150", "- and - and - and chicken 100", "- and - and - and - 150"};
int[] results = solution(info, query);
for (int result : results) {
System.out.println(result);
}
}
}
이진 검색을 활용한 로직 (성공)
package programmers;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class RankSearch {
static Map<String, List<Integer>> infoMap = new HashMap<>();
public static void preprocessInfo(String[] info) {
for (String i : info) {
String[] parts = i.split(" ");
int score = Integer.parseInt(parts[4]);
for (int a = 0; a < 2; a++) {
String lang = (a == 1) ? parts[0] : "-";
for (int b = 0; b < 2; b++) {
String field = (b == 1) ? parts[1] : "-";
for (int c = 0; c < 2; c++) {
String career = (c == 1) ? parts[2] : "-";
for (int d = 0; d < 2; d++) {
String food = (d == 1) ? parts[3] : "-";
String key = lang + " " + field + " " + career + " " + food;
infoMap.computeIfAbsent(key, k -> new ArrayList<>()).add(score);
}
}
}
}
}
for (String key : infoMap.keySet()) {
Collections.sort(infoMap.get(key));
}
}
public static int getAnswer(String query) {
String[] parts = query.replace(" and ", " ").split(" ");
String key = parts[0] + " " + parts[1] + " " + parts[2] + " " + parts[3];
int score = Integer.parseInt(parts[4]);
if (!infoMap.containsKey(key)) return 0;
List<Integer> scores = infoMap.get(key);
int left = 0, right = scores.size();
while (left < right) {
int mid = (left + right) / 2;
if (scores.get(mid) >= score) right = mid;
else left = mid + 1;
}
return scores.size() - left;
}
public static int[] solution(String[] info, String[] query) {
preprocessInfo(info);
int[] answer = new int[query.length];
for(int i = 0; i < query.length; i++) {
answer[i] = getAnswer(query[i]);
}
return answer;
}
public static void main(String[] args) {
String[] info = {"java backend junior pizza 150",
"python frontend senior chicken 210",
"python frontend senior chicken 150",
"cpp backend senior pizza 260",
"java backend junior chicken 80",
"python backend senior chicken 50"};
String[] query = {"java and backend and junior and pizza 100",
"python and frontend and senior and chicken 200",
"cpp and - and senior and pizza 250",
"- and backend and senior and - 150",
"- and - and - and chicken 100",
"- and - and - and - 150"};
solution(info, query);
}
}
나의 생각
| 정확도 통과, 효율성 실패 로직 | 이진 검색을 활용한 로직 |
|---|---|
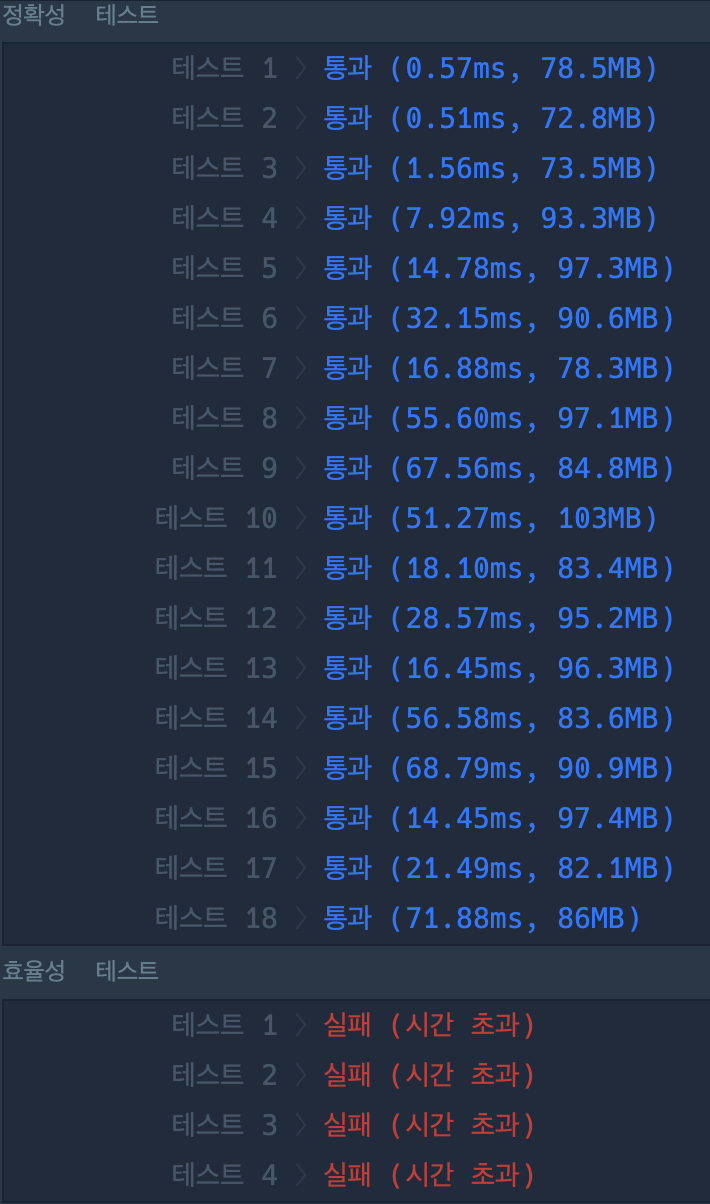 | 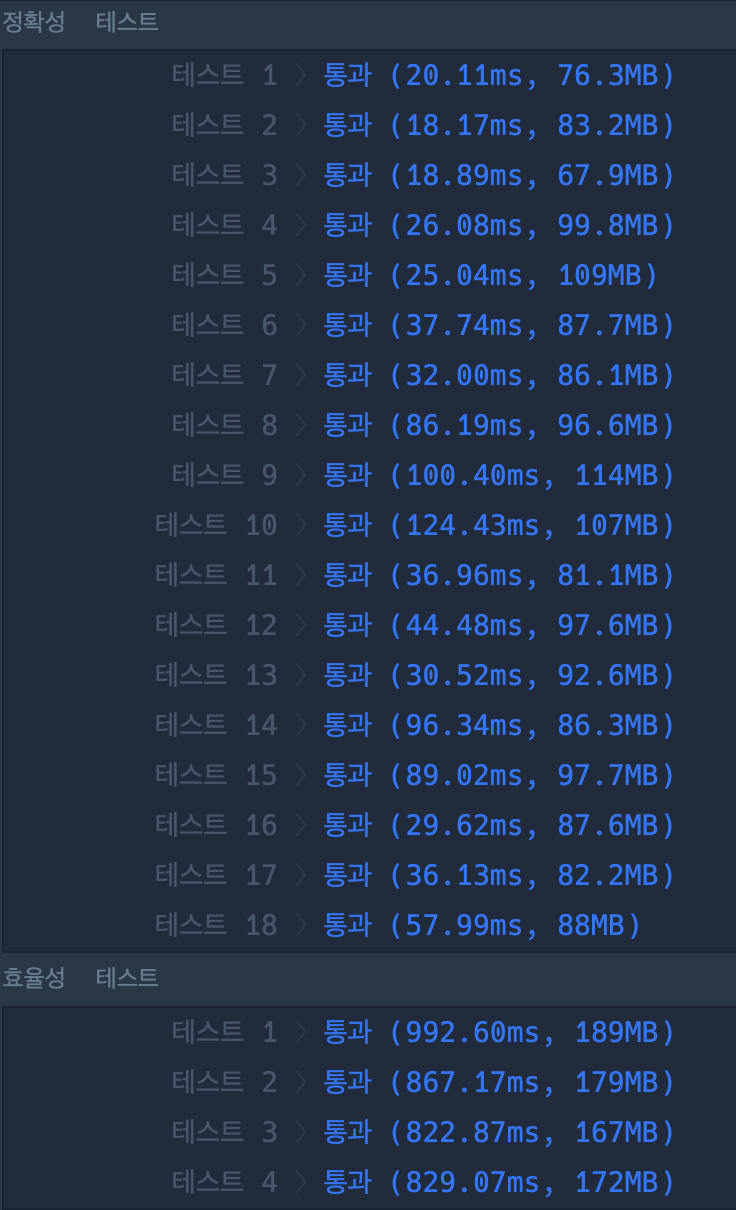 |
첫번째 로직은 각 쿼리에 대해 infoList의 모든 요소를 순회하면서 조건을 만족하는 지원자를 찾는 방식으로 작동함. 이 접근법은 각 쿼리마다 전체 infoList를 반복적으로 검사해야하므로, info의 길이나 query의 길이가 커질수록 매우 비효율적이다.
효율성 실패 이유
1. 리스트 전체 순회 : 각 쿼리마다 infoList를 처음부터 끝까지 순회하며
조건을 검사함. 이 과정은 O(N)의 시간 복잡도를 가짐. infoList의 길이가 길고
쿼리의 수가 많을수록 처리 시간이 기하급수적으로 증가함
2. 조건 검사의 중복 : 각 쿼리마다 모든 info 요소에 대해 동일한 조건 검사를 반복하게됨
이러한 중복된 계산은 비효율적임
개선점
1. 데이터 사전 처리 : info의 각 요소에 대해 가능한 모든 조건 조합을 미리 계산하고,
이에 해당하는 점수들을 저장하는 방식으로 데이터를 사전 처리함. 예를들어, hashMap을
사용하여 각 조건 조합에 대응하는 점수 리스트를 미리 생성할 수 있음
2. 이진 검색 활용 : 사전 처리된 데이터를 이용하여, 각 쿼리의 점수 조건에 대해
이진 검색을 수행. 이진 검색은 O(log N)의 시간 복잡도를 가지므로, 전체 리스트를
순회하는 것보다 훨씬 빠름
3. 조합의 효율적 저장 : 각 info 요소에 대한 모든 가능한 조건 조합
(예 : "java backend - -","- - senior chicken" 등)을 생성하고,
이 조합들에 대응하는 점수를 저장. 이렇게 하면 각 쿼리에 대해 조건에 맞는
점수 리스트를 빠르게 찾을 수 있음따라서, 나의 첫 로직구현 부분을 전체적으로 수정하였다.
- 전처리 구현
public static void preprocessInfo(String[] info) {
for (String i : info) {
String[] parts = i.split(" ");
int score = Integer.parseInt(parts[4]);
for (int a = 0; a < 2; a++) {
String lang = (a == 1) ? parts[0] : "-";
for (int b = 0; b < 2; b++) {
String field = (b == 1) ? parts[1] : "-";
for (int c = 0; c < 2; c++) {
String career = (c == 1) ? parts[2] : "-";
for (int d = 0; d < 2; d++) {
String food = (d == 1) ? parts[3] : "-";
String key = lang + " " + field + " " + career + " " + food;
List<Integer> scoresList;
if (infoMap.containsKey(key)) {
scoresList = infoMap.get(key);
} else {
scoresList = new ArrayList<>();
infoMap.put(key, scoresList);
}
scoresList.add(score);
}
}
}
}
}
for (String key : infoMap.keySet()) {
Collections.sort(infoMap.get(key));
}
}로직의 흐름
1. 데이터 분할 및 점수 파싱 : info 배열의 각 문자열을 분할하여 개발언어, 직군, 경력, 소울푸드, 점수를 추출
2. 가능한 모든 조건 조합 생성 : info 요소에 대해 가능한 모든 조건 조합을 생성.
이는 네가지 속성(언어, 직군, 경력, 소울푸드) 각각에 대해 실제 값을 사용하거나
`-`를 사용하는 것으로, 모든 가능한 조건을 포함
3. 조합별 점수 저장 : 생성된 각 조건 조합에 대해 해당 점수를 저장. 이때 infoMap
이라는 HashMap을 사용하여 각 조합(key)에 해당하는 점수 리스트를 관리
computeIfAbsent 메서드는 주어진 키에 대한 값이 없으면 새로운 ArrayList를
생성하고, 이미 존재하는 경우 해당 리스트를 반환
4. 점수 리스트 정렬 : 마지막으로 각 조건 조합에 해당하는 점수 리스트를 오름차순으로 정렬
정렬의 이유
- 마지막 단계에서 각 점수 리스트를 정렬하는 이유는 쿼리 처리 시 이진 검색을 통해
특정 점수 이상인 지원자들을 빠르게 찾기 위함
이진 검색은 정렬된 리스트에서만 효과적으로 작동하며, O(log N)의 시간 복잡도를
가지므로 매우 효율적임.
(정렬된 리스트를 사용하면 특정 점수 이상의 지원자 수를 찾기 위해 전체 리스트를
순회하는 대신 빠르게 결과를 도출할 수 있음)| 람다 표현식을 사용한 로직 구현 | if-else문으로 로직 구현 |
|---|---|
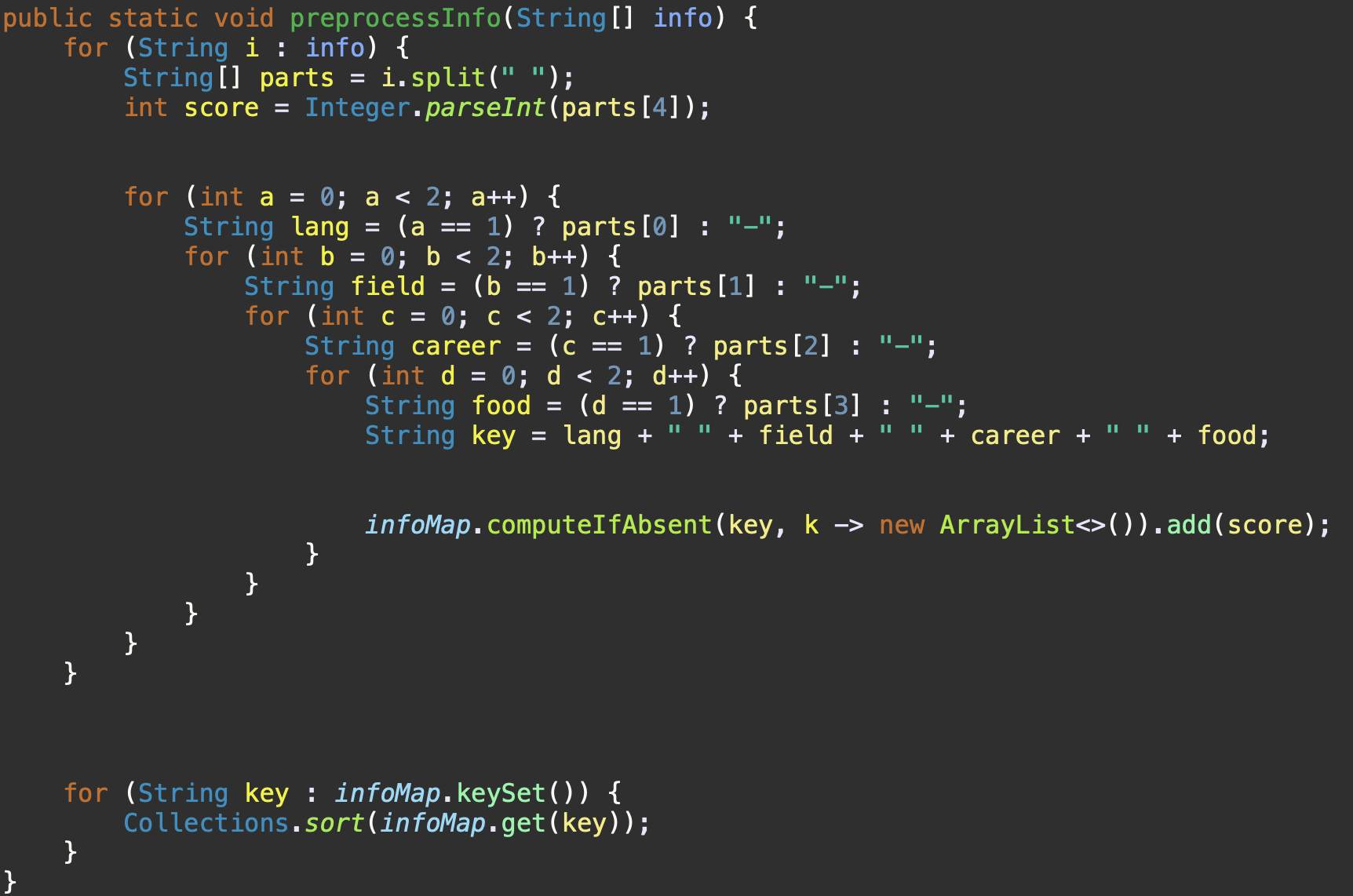 | 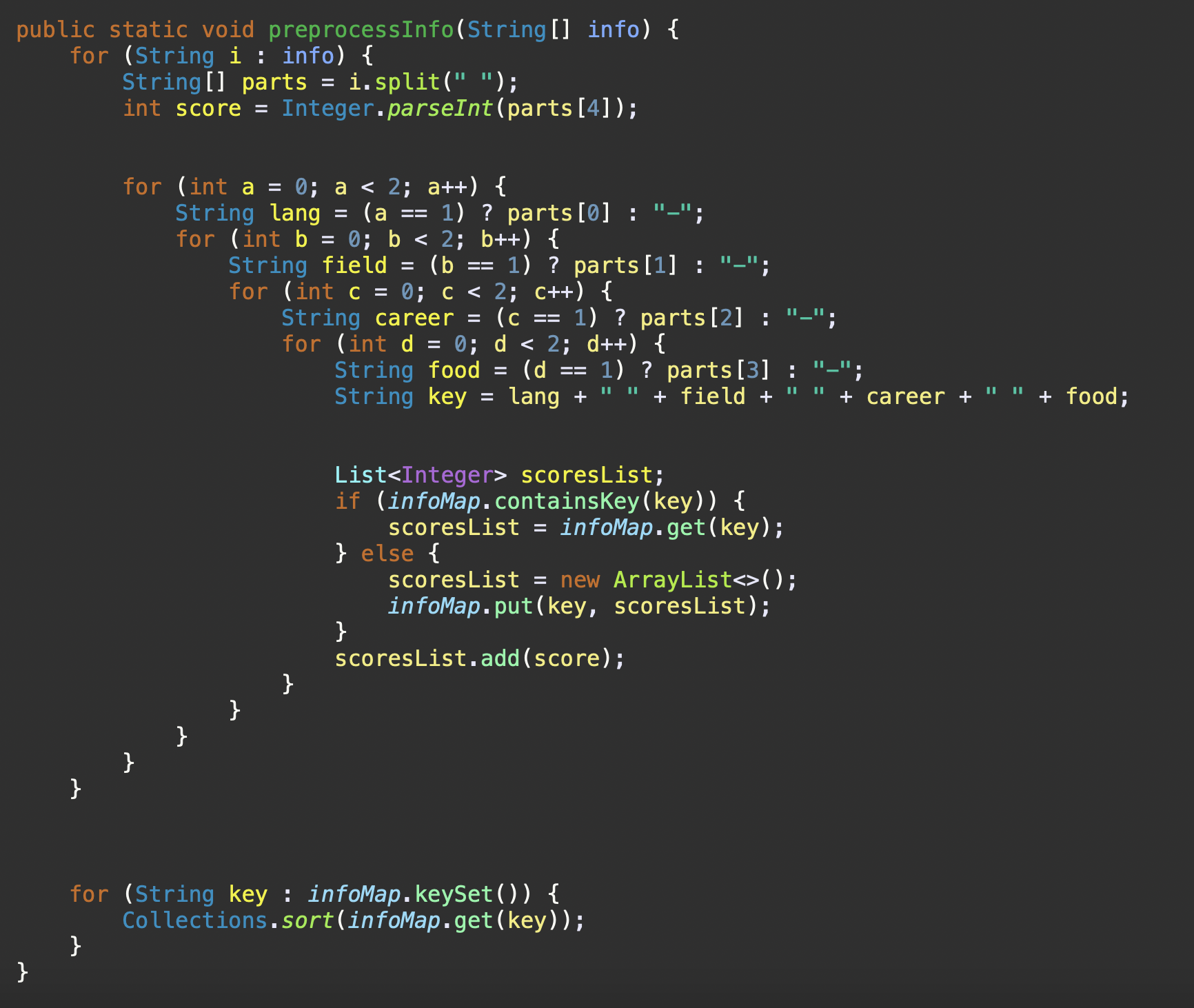 |
- 조건에 따른 지원자 수 계산
public static int getAnswer(String query) {
String[] parts = query.replace(" and ", " ").split(" ");
String key = parts[0] + " " + parts[1] + " " + parts[2] + " " + parts[3];
int score = Integer.parseInt(parts[4]);
if (!infoMap.containsKey(key)) return 0;
List<Integer> scores = infoMap.get(key);
int left = 0, right = scores.size();
while (left < right) {
int mid = (left + right) / 2;
if (scores.get(mid) >= score) right = mid;
else left = mid + 1;
}
return scores.size() - left;
}로직의 흐름
1. 쿼리 파싱 : 주어진 query 문자열에서 "and"를 기준으로 구분하고, 각 조건
(언어, 직군, 경력, 소울푸드)과 점수를 분리함
2. 조건 키 생성 : 분리된 조건들을 합쳐 하나의 키로 만듬. 이 키는 infoMap에서 사용
3. 점수 파싱 : 문자열로 된 점수를 정수로 변환
4. 점수 리스트 접근 : 만들어진 키를 사용해 infoMap에서 해당 조건에 맞는 점수 리스트를
가져옴. 해당 키가 존재하지 않으면 0을 반환
5. 이진 검색 실행 : scores 리스트에서 주어진 점수 이상인 첫 번째 요소의 인덱스를
찾기 위해 이진 검색을 수행함
- left는 검색 범위의 시작점, right는 끝점을 나타냄
- while 루프를 사용하여 left, right가 만날 때까지 범위를 반으로 줄여가며
중간점 mid에서 조건을 확인
- scores.get(mid) >= score인 경우, right를 mid로 이동시켜 범위를
왼쪽으로 줄임
- 그렇지 않으면 left를 mid + 1로 이동시켜 범위를 오른쪽으로 줄임
6. 결과 계산 및 반환 : 이진 검색이 완료된 후, scores.size() - left를 계산하여
주어진 점수 이상을 받은 지원자의 수를 반환정수 삼각형
문4) 아래와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
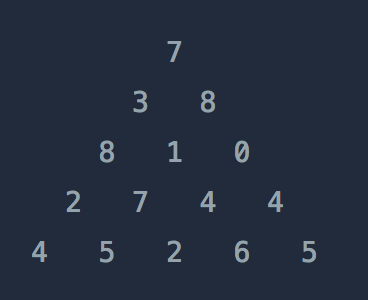
제한사항
- 삼각형의 높이는 1 이상 500 이하 입니다.
- 삼각형을 이루고 있는 숫자는 0 이상, 9,999 이하의 정수
입출력 예
| triangle | result |
|---|---|
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
나의 풀이
dfs 완전탐색 (시간초과 로직)
- 깊이가 500이라면 시간 초과할 것을 짐작함
- 재귀함수 공부에 목적을 두고 해당 방법으로도 시도해봄
package programmers;
public class IntegerTriangle {
static int[][] DIRS = {{1, 0}, {1, 1}};
static int MAX;
public static void dfs(int y, int x, int sum, int[][] triangle) {
if(y == triangle.length - 1) {
MAX = Math.max(MAX, sum);
return;
}
for(int[] dir : DIRS) {
int newY = y + dir[0];
int newX = x + dir[1];
if(newX < triangle[newY].length) {
dfs(newY, newX, sum + triangle[newY][newX], triangle);
}
}
}
public static int solution(int[][] triangle) {
MAX = Integer.MIN_VALUE;
dfs(0, 0, triangle[0][0], triangle);
System.out.println(MAX);
return MAX;
}
public static void main(String[] args) {
int[][] triangle = {{7}, {3, 8}, {8, 1, 0}, {2, 7, 4, 4}, {4, 5, 2, 6, 5}};
solution(triangle);
}
}
동적계획법(Dynamic Programming)을 적용한 로직
package programmers;
import java.util.Arrays;
public class IntegerTriangle {
public static int solution(int[][] triangle) {
int n = triangle.length;
// 동적 계획법을 위한 2차원 배열을 초기화
// 각 요소는 해당 위치까지의 최대 합을 저장
int[][] dp = new int[n][n];
// 삼각형의 꼭대기부터 시작함
dp[0][0] = triangle[0][0];
// 삼각형의 각 레벨에 대해 반복
for(int i = 1; i < n; i++) {
// 각 레벨의 시작점을 계산, 항상 왼쪽 끝
dp[i][0] = dp[i - 1][0] + triangle[i][0];
// 각 레벨의 끝점을 계산, 항상 오른쪽 끝
dp[i][i] = dp[i - 1][i - 1] + triangle[i][i];
// 삼각형의 해당 레벨에서 각 위치까지의 최대 합을 계산
for (int j = 1; j < i; j++) {
// 최대 합은 위쪽 두 위치 중 더 큰 값에 현재 값(triangle[i][j])을 더한 것
dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];
}
}
// 삼각형의 바닥에서 가능한 최대 합을 찾기 시작
int maxSum = dp[n - 1][0];
// 바닥의 각 위치를 순회하며 최대 합을 찾음
for (int i = 1; i < n; i++) {
maxSum = Math.max(maxSum, dp[n - 1][i]);
}
return maxSum;
}
public static void main(String[] args) {
int[][] triangle = {{7}, {3, 8}, {8, 1, 0}, {2, 7, 4, 4}, {4, 5, 2, 6, 5}};
solution(triangle);
}
}
나의 생각
Bottom-Up 방식 사용: 삼각형의 바닥부터 시작하여 위로 올라가며,
각 단계에서 가능한 최대 합을 계산
각 단계의 최대 합 계산: 각 단계에서 해당 요소에 도달할 수 있는 경로 중
최대 합을 저장. 이 값은 현재 요소의 값과 그 아래 단계의 두 인접 요소 중
더 큰 값의 합으로 결정
최종 결과 반환: 최상단 요소에서의 최대 합이 전체 삼각형의 최대 합이 됨
이 방법은 각 요소를 한 번만 방문하므로, 시간 복잡도는 O(N^2)가 됨
N은 삼각형의 높이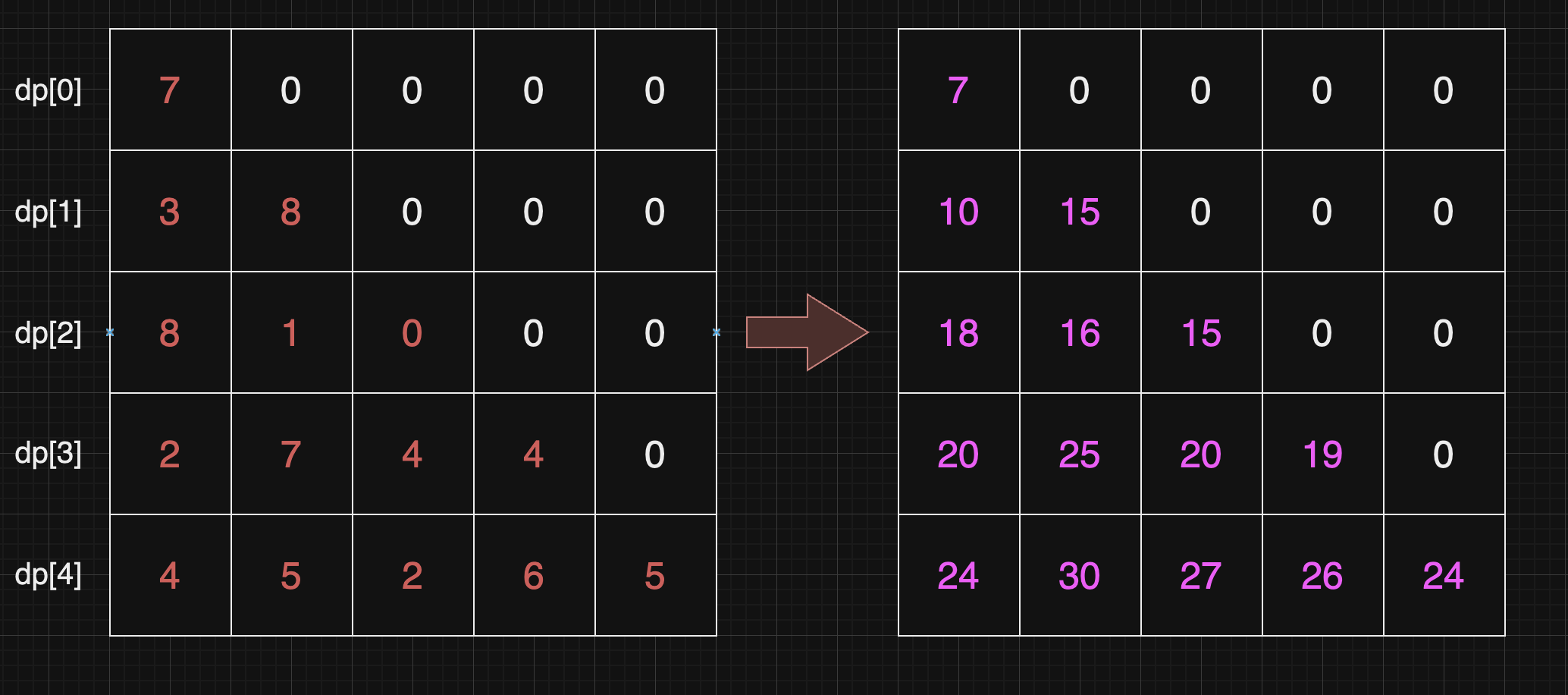
이중 우선순위 큐
문5) 이중 우선순위 큐는 다음 연산을 할 수 있는 자료구조를 말합니다.
| 명령어 | 수신 탑(높이) |
|---|---|
| I 숫자 | 큐에 주어진 숫자를 삽입합니다. |
| D 1 | 큐에서 최댓값을 삭제합니다. |
| D -1 | 큐에서 최솟값을 삭제합니다. |
이중 우선순위 큐가 할 연산 operations가 매개변수로 주어질 때, 모든 연산을 처리한 후 큐가 비어있으면 [0,0] 비어있지 않으면 [최댓값, 최솟값]을 return 하도록 solution 함수를 구현해주세요.
제한사항
- operations는 길이가 1 이상 1,000,000 이하인 문자열 배열입니다.
- operations의 원소는 큐가 수행할 연산을 나타냅니다.
- 원소는 “명령어 데이터” 형식으로 주어집니다.- 최댓값/최솟값을 삭제하는 연산에서 최댓값/최솟값이 둘 이상인 경우, 하나만 삭제합니다.
- 빈 큐에 데이터를 삭제하라는 연산이 주어질 경우, 해당 연산은 무시합니다.
입출력 예
| operations | return |
|---|---|
["I 16", "I -5643", "D -1", "D 1", "D 1", "I 123", "D -1"] | [0,0] |
["I -45", "I 653", "D 1", "I -642", "I 45", "I 97", "D 1", "D -1", "I 333"] | [333,-45] |
입출력 예 설명
입출력 예 #1
- 16과 -5643을 삽입합니다.
- 최솟값을 삭제합니다. -5643이 삭제되고 16이 남아있습니다.
- 최댓값을 삭제합니다. 16이 삭제되고 이중 우선순위 큐는 비어있습니다.
- 우선순위 큐가 비어있으므로 최댓값 삭제 연산이 무시됩니다.
- 123을 삽입합니다.
- 최솟값을 삭제합니다. 123이 삭제되고 이중 우선순위 큐는 비어있습니다.
따라서 [0,0]을 반환합니다.
입출력 예 #2
- -45와 653을 삽입후 최댓값(653)을 삭제합니다. -45가 남아있습니다.
- -642, 45, 97을 삽입 후 최댓값(97), 최솟값(-642)을 삭제합니다. -45와 45가 남아있습니다.
- 333을 삽입합니다.
이중 우선순위 큐에 -45, 45, 333이 남아있으므로, [333, -45]를 반환합니다.
나의 풀이
package programmers;
import java.util.Comparator;
import java.util.PriorityQueue;
public class DualPriorityQueue {
public static int[] getMaxMin(PriorityQueue<Integer> pq) {
PriorityQueue<Integer> reversePq = new PriorityQueue<>(Comparator.reverseOrder());
reversePq.addAll(pq);
if(pq.isEmpty()) return new int[] {0,0};
return new int[] {reversePq.poll(), pq.poll()};
}
public static int[] solution(String[] operations) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
for(int i = 0; i < operations.length; i++) {
char command = operations[i].charAt(0);
int num = Integer.parseInt(operations[i].split(" ")[1]);
if(command == 'I') {
pq.add(num);
}else { // command == 'D'
if(!pq.isEmpty()) {
if(num == -1) {
pq.remove();
}else {
PriorityQueue<Integer> descendingPq = new PriorityQueue<>(Comparator.reverseOrder());
descendingPq.addAll(pq);
pq.remove(descendingPq.poll());
}
}
}
}
return getMaxMin(pq);
}
public static void main(String[] args) {
String[] operations = {"I -45", "I 653", "D 1", "I -642", "I 45", "I 97", "D 1", "D -1", "I 333"};
solution(operations);
}
}
나의 생각
문제의 로직을 먼저 분석해보면, command I, D 두가지 명령어로 분류되고, I(insert) 동작에서는 특정 수를 삽입, D(delete) 동작에서는 특정수를 제거 하는데, D동작에서는 다시 두 가지 (1, -1)로 분류 할 수 있다.
즉, I 명령이 들어오면 우선순위 큐 pq에 삽입만하고, D 명령이 들어오면 " " 공백 뒤 오는 다음 숫자가 1 또는 -1에 따라 동작을 다르게 한다. 하지만 D 명령이 들어왔을 때 다음 숫자 (1 또는 -1)에 따라 최대값, 최소값을 제거해야하는데 최소값은 우선 순위 큐 자체가 오름차순으로 정렬되어있기때문에 바로 사용할 수 있지만, 최대값을 제거해야하는 부분은 새로운 reversePq를 선언하고 이를 내림차순으로 정렬하여 첫 번째 값을 제거하는 방법을 사용하였다.
핵심 로직을 보면 다음과 같다.
PriorityQueue<Integer> pq = new PriorityQueue<>();
for(int i = 0; i < operations.length; i++) {
char command = operations[i].charAt(0);
int num = Integer.parseInt(operations[i].split(" ")[1]);
if(command == 'I') {
pq.add(num);
}else { // command == 'D'
if(!pq.isEmpty()) {
if(num == -1) {
pq.remove();
}else {
PriorityQueue<Integer> descendingPq = new PriorityQueue<>(Comparator.reverseOrder());
descendingPq.addAll(pq);
pq.remove(descendingPq.poll());
}
}
}
}char command는 매개변수 operations 에서 명령어만 따로 분리한다.
int num 변수는 매개변수 operations에서 공백 다음 오는 문자를 Integer형태로 변환하여 숫자로 나타내는데, command D가 들어오면 1 또는 -1인지 판별하여 다음 동작을 진행시킨다.
특히, D 1이 들어왔을 때 동작을 보면
else {
PriorityQueue<Integer> descendingPq = new PriorityQueue<>(Comparator.reverseOrder());
descendingPq.addAll(pq);
pq.remove(descendingPq.poll());
} 내림차순형태의 descendingPq를 선언하여 오름차순형태의 pq의 값들을 그대로 추가하여
내림차순하여 첫 번째 값을 pq.remove() 를 통해 값을 넣어 바로 제거 한다.
pq.remove(descendingPq.poll());
그리고 명령어로 필터된 pq에서 최대값, 최소값을 리턴하기위해 다음과 같은 로직을 수행한다.
public static int[] getMaxMin(PriorityQueue<Integer> pq) {
PriorityQueue<Integer> reversePq = new PriorityQueue<>(Comparator.reverseOrder());
reversePq.addAll(pq);
if(pq.isEmpty()) return new int[] {0,0};
return new int[] {reversePq.poll(), pq.poll()};
}
- 블로그에 내용을 정리하다가 불필요한 로직이 보여 로직을 수정하였다.
package programmers;
import java.util.Comparator;
import java.util.PriorityQueue;
public class DualPriorityQueue {
public static int[] solution(String[] operations) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
PriorityQueue<Integer> descendingPq = new PriorityQueue<>(Comparator.reverseOrder());
for(String operation : operations) {
String[] parts = operation.split(" ");
char command = parts[0].charAt(0);
int num = Integer.parseInt(parts[1]);
if(command == 'I') {
pq.add(num);
descendingPq.add(num);
}else if(command == 'D') {
if(!pq.isEmpty()) {
if(num == 1) {
int max = descendingPq.poll();
pq.remove(max);
}else {
int min = pq.poll();
descendingPq.remove(min);
}
}
}
}
if(pq.isEmpty()) {
return new int[] {0,0};
}else {
return new int[] {descendingPq.peek(), pq.peek()};
}
}
public static void main(String[] args) {
String[] operations = {"I -45", "I 653", "D 1", "I -642", "I 45", "I 97", "D 1", "D -1", "I 333"};
solution(operations);
}
}
