
5점 요약 표시
최솟값
제 1사분위수 ( )
제 2사분위수( ), 즉 중앙값
제 3 사분위 수( )
최댓값
예상문제[INC/EXC/평균보다 낮은 값?]
왜도와 첨도
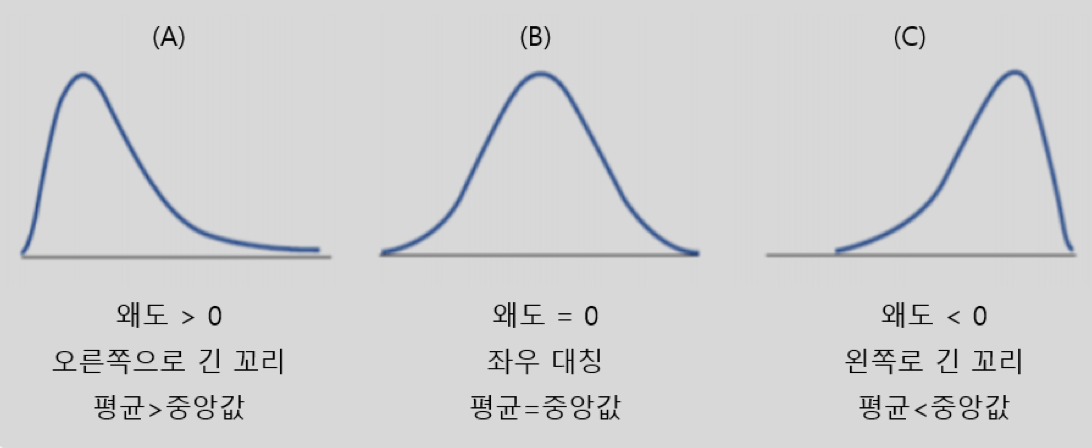
왜도(skewness)(또는 비대칭도)
-분포의 대칭이나 비대칭의 정도를 표시하는 척도
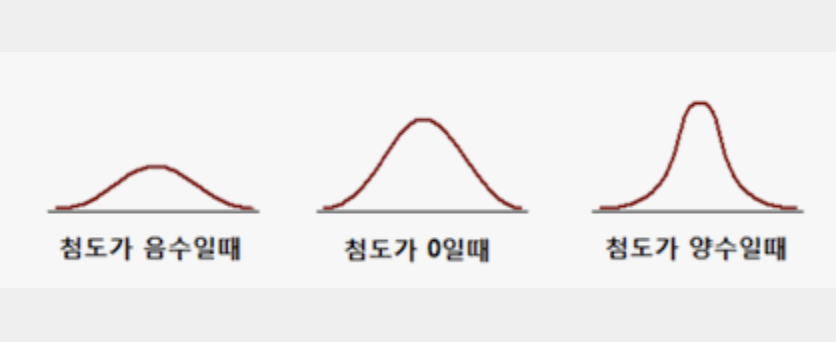
척도(kurtosis)
-뾰족함의 정도를 나타내는 척도
🌟상자그림
분포의 대칭성, 자료의 중심 위치, 산포도(또는 흩어진 정도), 분포의 꼬리 부분에서의 집중 정도 등을 파악하는데 상자그림이 필요하다.
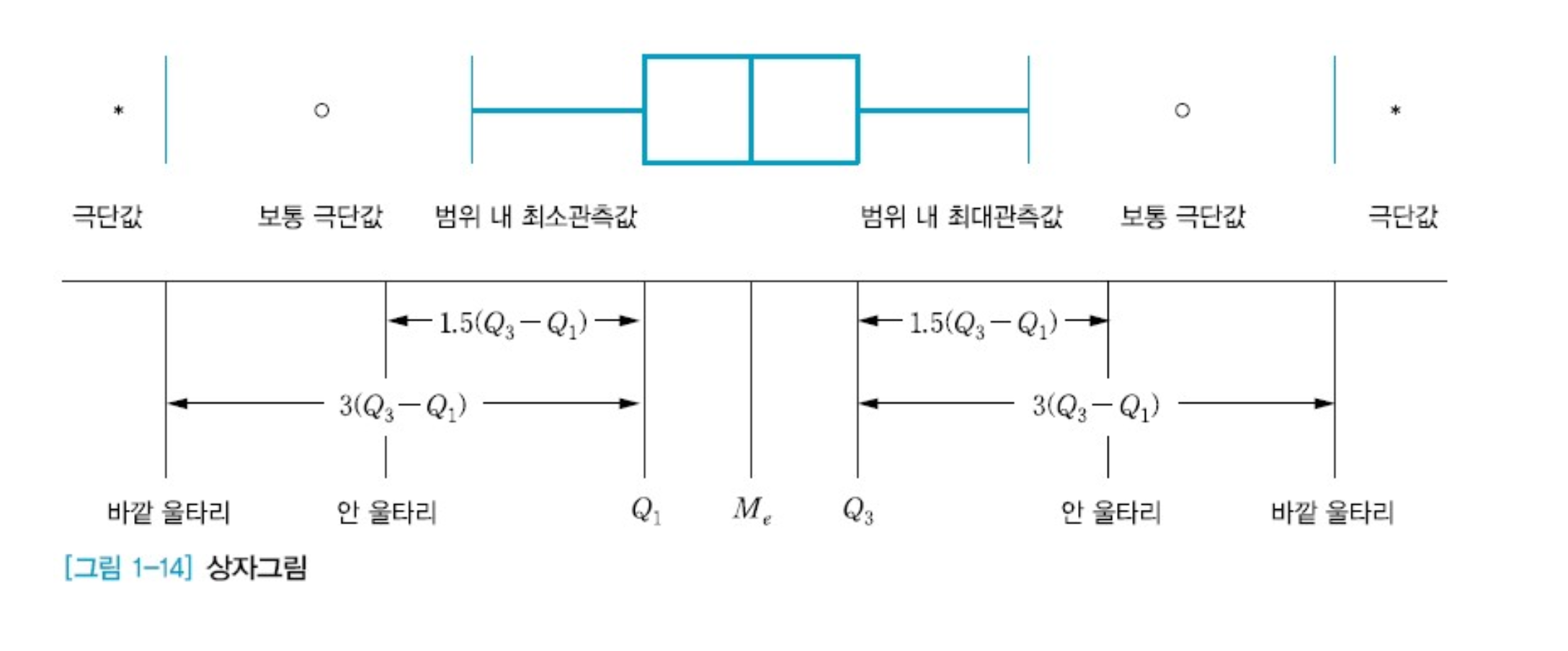
상자 그림(box plot)
-
사분위수를 이용하여 수집한 자료에 포함된 특이값을 알려주는 그림
-
자료의 중심 위치와 흩어진 모양 그리고 분포의 꼬리 부분을 쉽게 파악할 수 있음
-
두 개 이상의 자료 집단 비교할 때 유용함
-
순서
- 사분위수 구함
- 사분위수 범위 구함
- 사분위수 범위(interquartile range/I.Q.R): Q3 - Q1
- Q1에서 Q3까지 직사각형 모양의 상자 그리고, 중위수 Q2 위치인 상자 안에 수직선 그음
- 안울타리를 구하고 인접값에 기호 '|'로 표시한 후, 각각 Q1과 Q3으로부터 인접값까지 선분으로 연결하여 상자 그림의 날개 부분 작성
- 안울타리(inner fence): 사분위수 Q1, Q3에서 각각 (1.5 * 사분위수 범위) 만큼 떨어져 있는 값
- 인접값(adjacent value): 안울타리 안에 놓이는 가장 극단적인 자료값, 즉 왼쪽 안울타리
보다 큰 자료값 중에서 가장 작은 자료값과 오른쪽 안울타리보다 작은 자료값 중에서 가장 큰 자료값
- 바깥울타리를 구하여 관측 가능한 보통 특이값의 위치에 'O', 특이값의 위치에 'X'로 표시
- 바깥울타리(outer fence): 사분위수 Q1, Q3에서 각각 (3 * 사분위수 범위) 만큼 떨어져 있는 값
- 보통 특이값(mild outlier)/보통 극단값: 안울타리와 바깥울타리 사이에 놓이는 자료값
- 특이값(extreme outlier)/극단값: 바깥울타리 외부에 놓이는 자료값
- 위 box plot 해석
- 중심부 50%(사분위수 범위)의 자료는 중앙값을 중심으로 대칭적이지 않음 -> 중앙값이 왼쪽으로 쏠려 있는 것으로 보아 중심부 50%의 자료 내에서는 중앙값을 기준으로 하여 오른쪽으로 더 길게 분포함
- 박스가 오른쪽으로 좀 더 가 있음 -> 왼쪽 날개 부분이 오른쪽 날개 부분보다 김
- 측정 가능한 보통 특이값은 3개, 특이값은 2개