모집단과 표준

01모집단과 표본

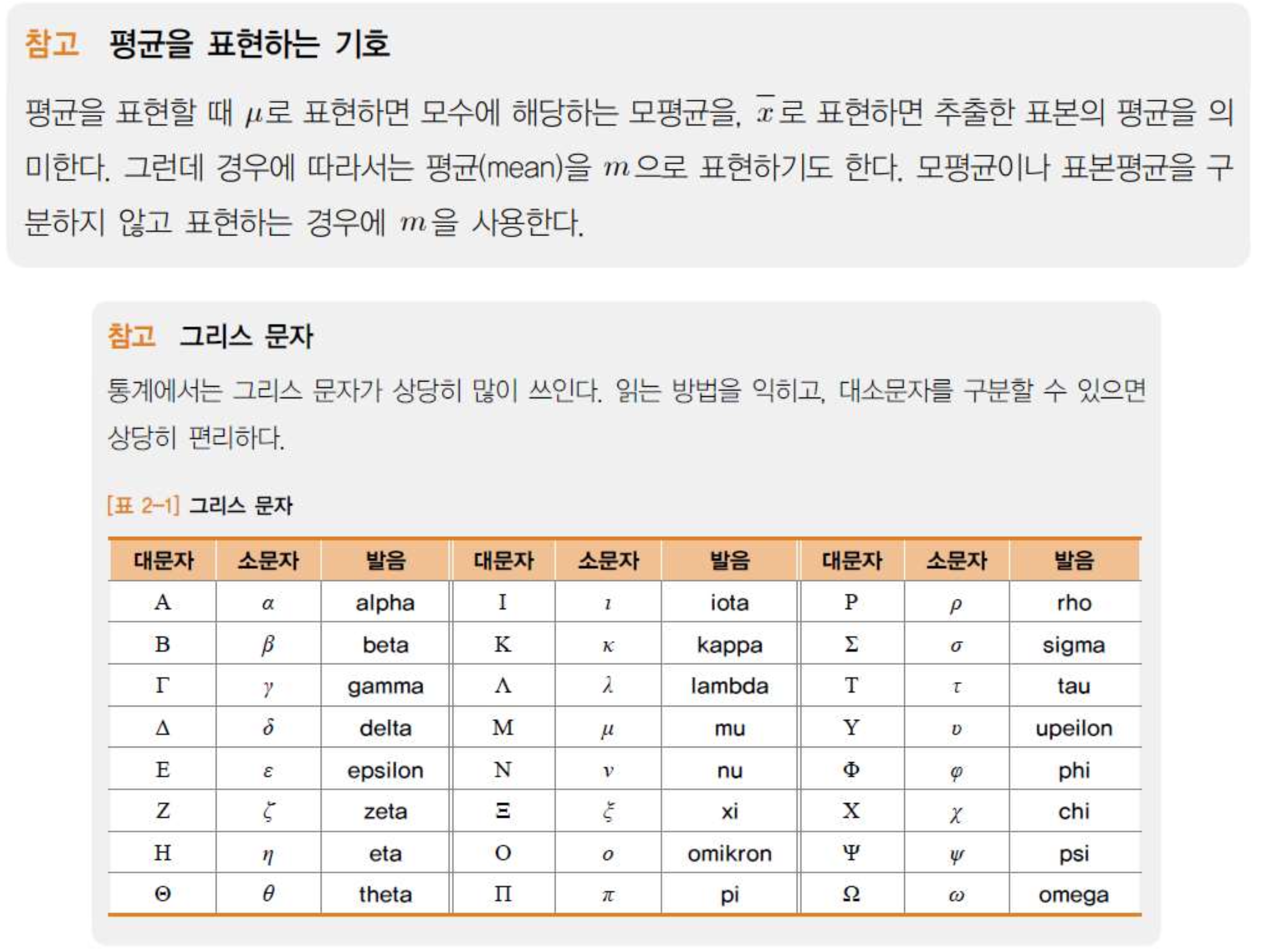
*epsilon/eta/lambda/mu/sigma/tau/chi/omerga

모집단(population): 통계분석 방법을 적용할 관심 대상의 전체 집합

표본(sample): 과학적인 절차를 적용하여 모집단을 대표할 수 있는 일부를 추출하여 직접적인 조사 대상이 된 모집단의 일부

모수(parameter): 모집단을 분석하여 얻어지는 결과 수치
ex. 모평균, 모분산, 모표준편차, 모비율

통계량(statistic): 표본을 분석하여 얻어지는 결과 수치
ex. 표본평균, 표본분산, 표본표준편차, 표본비율

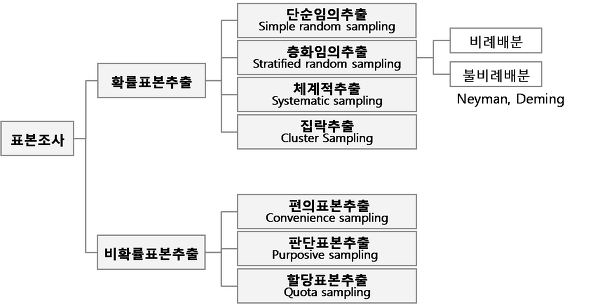
표본추출 방법

-확률적 표본추출 방법(probability sampling method): 모집단의 구성요소들이 표본이 될 확률이 모두 동일
-비확률적 표본추출 방법(non-probability sampling method): 조사자의 의지 또는 조사 대상이 자발적으로 표본을 구성

확률적표본추출

-단순 무작위 표본추출: 모집단에서 일정한 규칙에 따라 표본을 기계적으로 추출하는 방법
ex. 컴퓨터로 추출하거나 난수표를 활용
-체계적 표본추출: 모집단에 번호를 부여하고 일정한 n개의 간격으로 표본을 추출하는 방법
예)선거 당일 출구에서 투표를 하고 나오는 유권자의 숫자를 세어 1,11,21,31,41,번째(혹은 1,101,201,301,번째)의 유권자를 대상으로 조사하는 경우
-비례 층화 표본추출: 모집단을 여러 개의 이질적 집단으로 구분한 후, 각 집단의 구성 개수에 비례하도록 추출하는 방법
예)총원 10,000명인 대학교에서 1,2,3,4학년의 비율은 4:3:2:1이다. 1,000명을 추출하고자 할 때, 각 학년을 구성하는 비율대로 학년별로 각각 400, 300,200,100명씩 추출하여 1,000명의 표본을 구성하는 방법
-다단계 층화 표본추출: 비례 층화 표본추출에서 상-하위 표본 단위를 미리 설정하고 그에 맞추어 다시
추출하는 방법
예)총원이 10,000명인 A대학교에서 1,000명을 추출할 때, 먼저 단과 대학별로 구분지은 후 다시 학과별 구성에 맞춰 표본을 추출하는 방법

-군집 표본추출: 모집단의 구성이 내부 이질적이면서 외부 동질적으로 구성되어 있다면, 모집단 전체를 조사하지 않고 몇 개의 군집을 표본으로 선택해서 조사하는 방법
예)서울 시민을 대상으로 자전거의 구매의사를 조사할 때, 25개 구를 모두 조사하지 않고 표본으로 몇 개의 구를 선택하여 조사

비확률적 표본추출(표본 구성확률 다름)

-편의 표본추출: 조사자 임의, 실수 오류 많다. 비용 적음
-판단 표본추출: 구성원 적합 판단
-할당 표본추출: 모집단 속성 대표할만한 연령,학력,직업 분류 후 각각 표본개수를 결정한 후 조사자가 임의적으로 할당
-자발적 표본추출: 표본들이 스스로 와서, 해당문제에 대해 관심 있는 사람이 표본. 결과 왜곡 확률 가장 높음

02표본의 분포

정규분포
표본분포 중 가장 단순하면서 많이 나타나는 형태의 분포
-어떤 사건이 일어난 빈도(frequency)를 계산하여 그래프로 나타내면 중심(평균)을 기준으로 좌우가 대칭되는 분포

표준화
(기준 중심 새 배치. 평균=0 분산(표준편차)=1, 루트 씌워도 1이라)

단순한 현상은 정규분포만을 이용해도 결과를 알아내는 데 문제가 없지만 대부분의 연구에서는 복잡한 관계에 대한 분석 결과가 필요하므로, 여러 특성에 대한 분석 결과들을 서로 비교할 수 있도록 만드는 과정(평균이나 측정단위가 다를 경우)

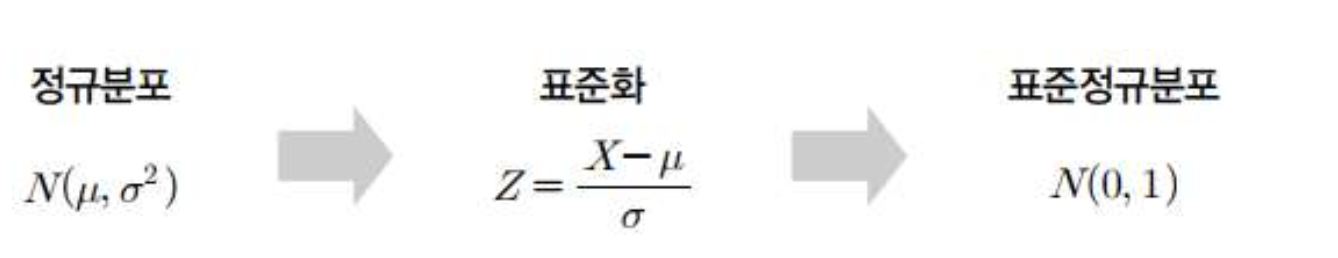
z분포
: 표본의 개수가 충분할 때 표준화 과정을 거친 정규분포를 표준정규분포(standard normal distribution), 혹은 z분포라고 한다.
->표준정규분포는 ‘평균=0, 분산=1’인 정규분포를 따른다.

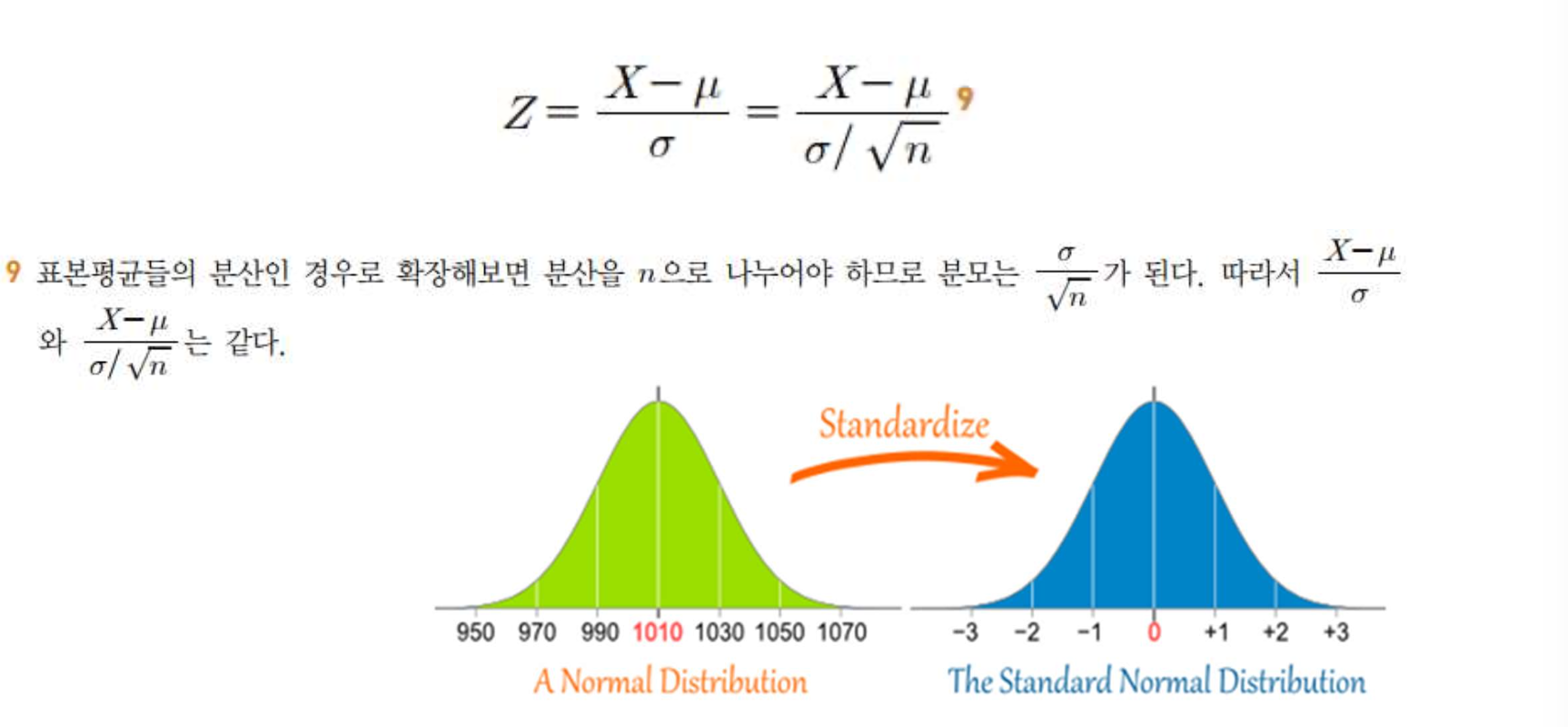
t분포
: 표본이충분하지못한경우⭐️(n<30)에 분포를사용
모집단은 정규분포를 이룬다는 가정이 필요하며, t분포도 ‘평균=0, 분산>1’인
정규분포를 따른다.

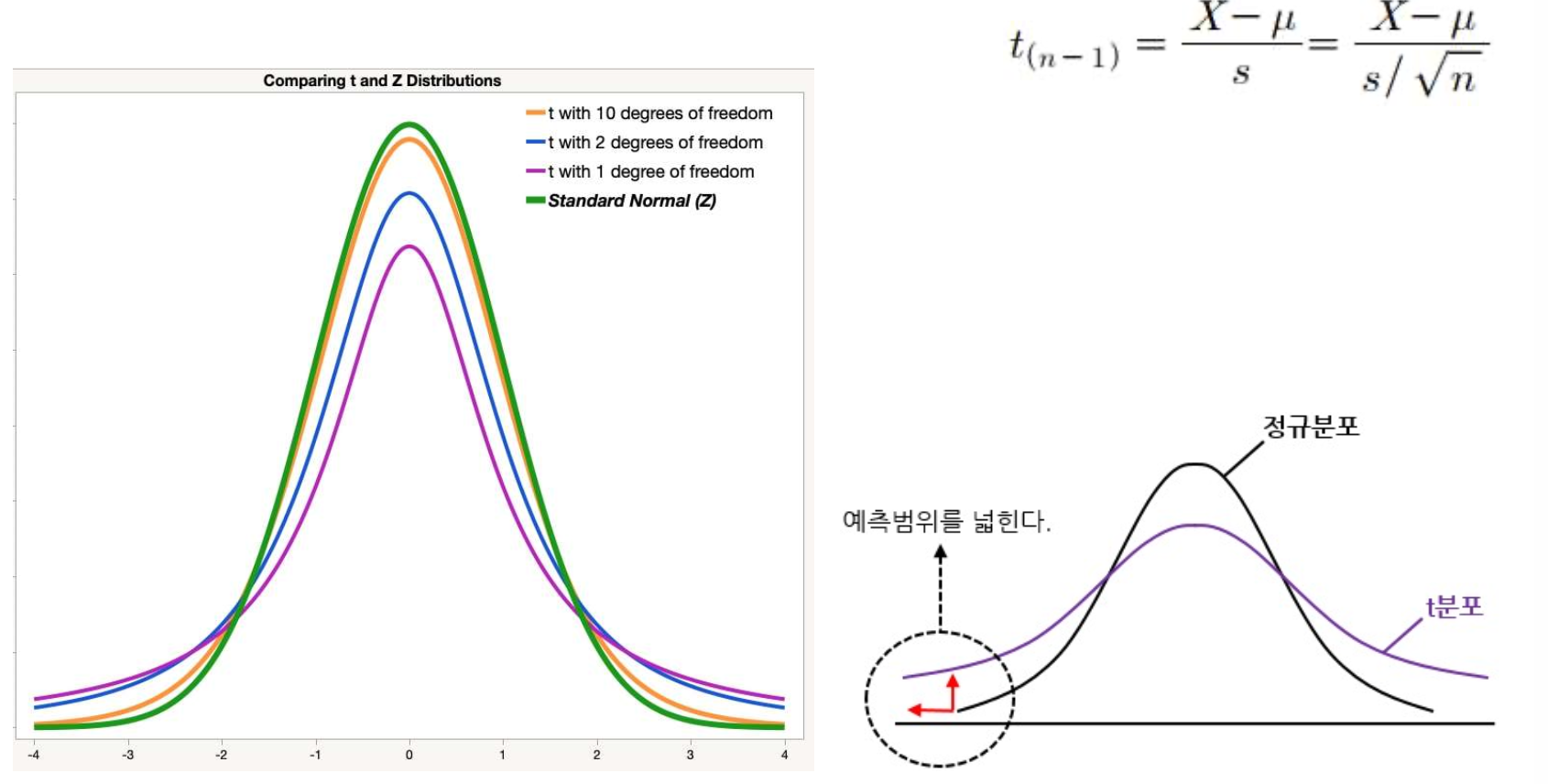
*t분포 정규분포보다 봉우리 낮고 옆으로 퍼짐->날개 높다

⭐️z분포와 t분포의 관계

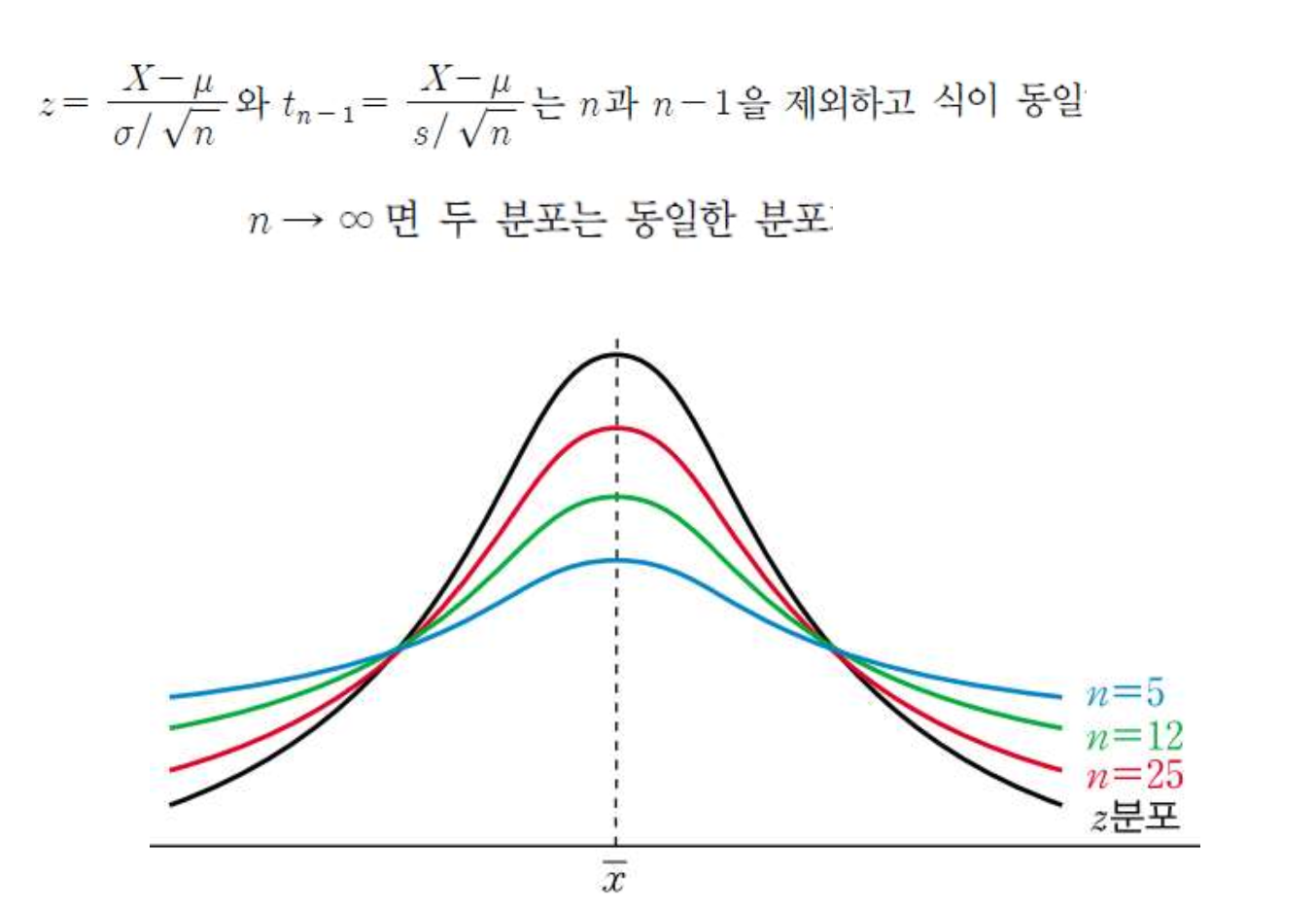
*z분포 같게

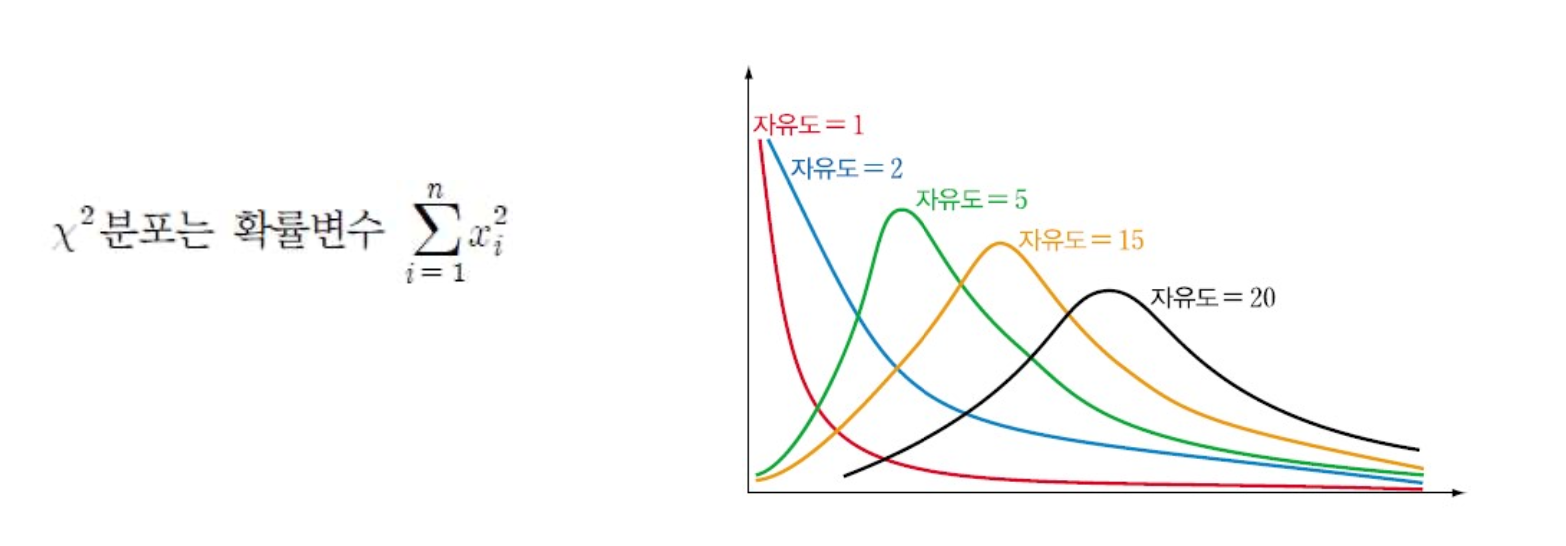
χ 2 카이제곱분포

표준정규분포에서 도출, z분포에 대한 제곱의 값을 분포 >0

확률변수 x1, x2, x3... xn이 표준정규분포이면서 독립이라면 새 확률변수 구성 자유도가 n 인 카이제곱분포 구성

자유도 늘어날수록 정규분포에 근접

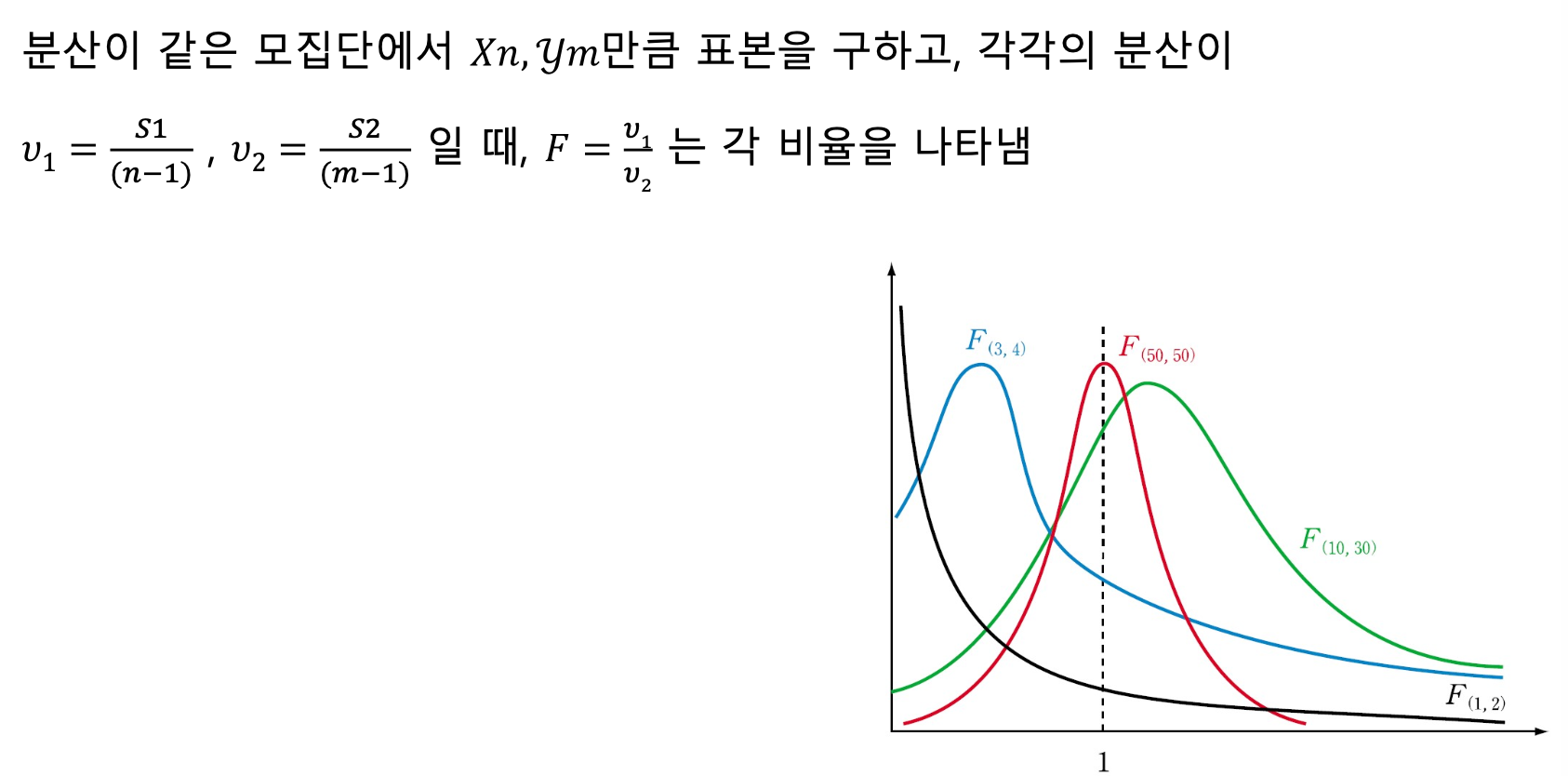
F분포
카이제곱분포에 대한 두 개의 분산에 관한 추론 F(v1,v2)

자유도 기준 비율을 나타냄. 1기준 양쪽이 대칭인 그래프

p^은‘p-hat(피 햇)’(표본비율)분포, 비율분포

모집단의 특성 중 모비율을 추정하기 위해 사용됨.

어느 한 사건이 발생하는 베르누이 시행의 이항분포를 활용하여 표본비율의 분포를 구한다.

*이항분포 B(n,p)의 평균 E(X)=np, 분산 V(X)=npq

03 표본 분포와 중심극한정리

표본분포(sample distribution)는 표본에서 도출되는 통계량에 대한 확률분포-> 표본분포는 모수를 추정하기 위한 표본 통계량의 확률분포(여러 번 측정)

모집단의 구성 5개, 표본 3개 추출과 2개 추출하는 경우 10가지, 각 경우에 수에 대한 평균 비교해보면 평균 분포 3개일 때 분산이 작아진다. 모평균 기준 표본 평균의 오차 확인하면 3개일 때 평균 오차가 분산간격이 작음.
*표본의 개수가 늘어날수록 통계량이 모수와 가까워짐

표본평균의 오차:표본으로부터 모수를 추정했을 때, 모수와 통계량 간의 차이

중심극한정리(Central Limit Theorem : CLT)
는 표본의 개수(n)가 충분하다면 모수를 모르는 상황에서도 표본 통계량으로 정규분포를 구성하여 모수를 추정할 수 있다는 것이다.
->중심국한정리에서는 모집단이 정규분포를 이루지 않아도 표본의 개수가 충분하다면 정규분포를 이루게 된다.
샘플수가 ⭐️30개이상이면 정규분포에 다가서기 때문에 이를 이용하여 연구를 수행할 수 있다.
참고자료