
<산술평균>
-몇 가지 항목의 수치를 합계한 값을 그 항목수로 나눈 것이다.
-산술평균 - 가중산술평균, 단순산술평균
- 가중산술평균
ㅇ 자료의 평균을 구할 때 자료 값의 중요도나 영향 정도에 해당하는 가중치를 반영하여 구한 평균값
표본평균x̄
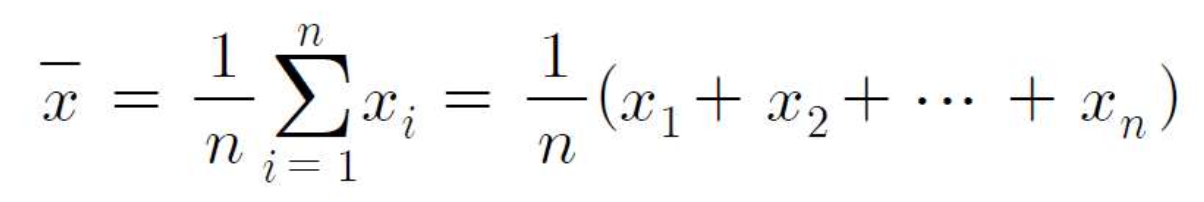
-변량 X에 대한 n개의 자료가 주어질때 x1, x2,...xn, 변량 X의 산술평균을 표본평균
모평균μ
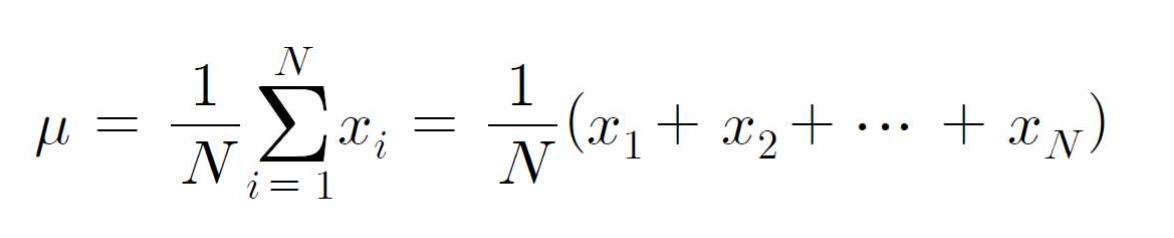
-변량 X가 모집단에서 얻는 관측값이 x1, x2,...xN으로 주어질때, 변량 X의 산술평균을 표본평균
가중산술평균
-변량 X의 자료가 계급형 도수분포료로 주어질때, 다음과 같이 구한다.
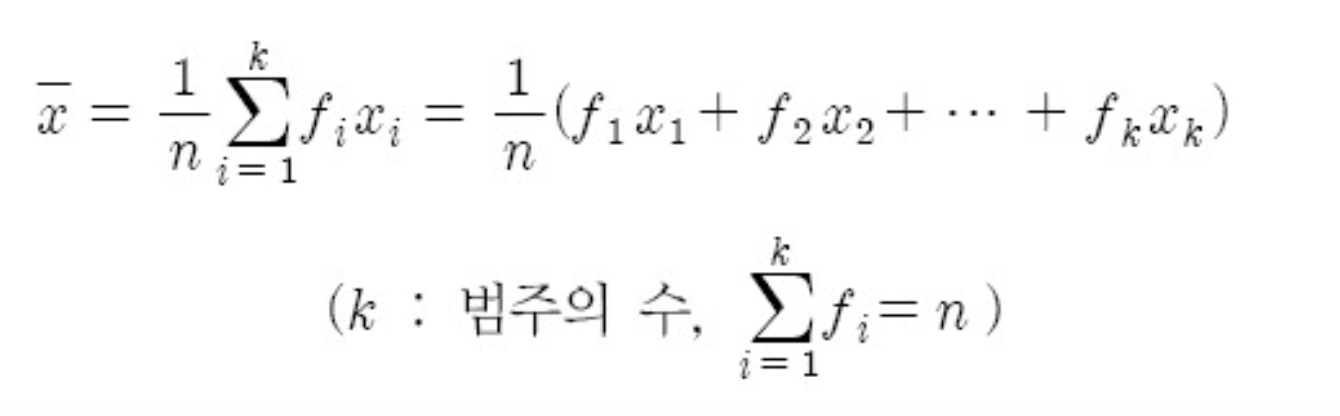
🌟산술평균의 성질
관측값-평균

중앙값=중위수
작은 값부터 크기순으로 배열했을때, 한가운데 위치한값

-중앙값은 다음과 같이 편차의 절댓값의 합을 최소로 하는 성질이 있다.
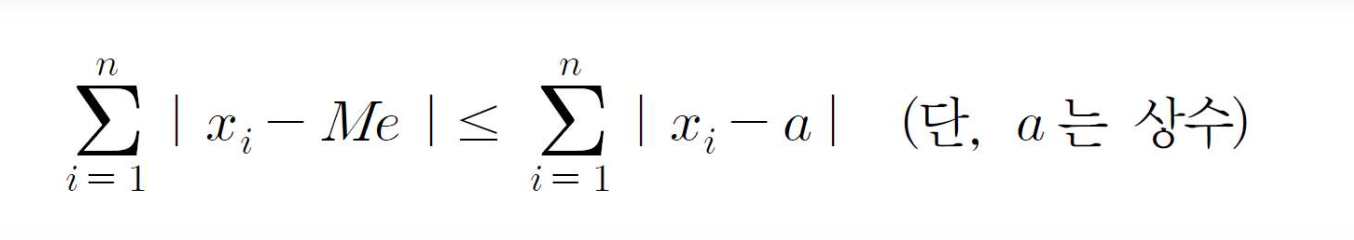
최빈값
자료 중에서 가장 많이 나타나는 값
-두 개 이상일 수도 있고, 없을 수도 있다
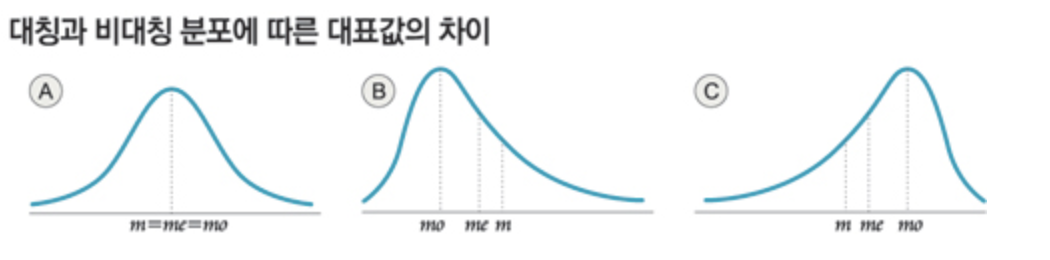
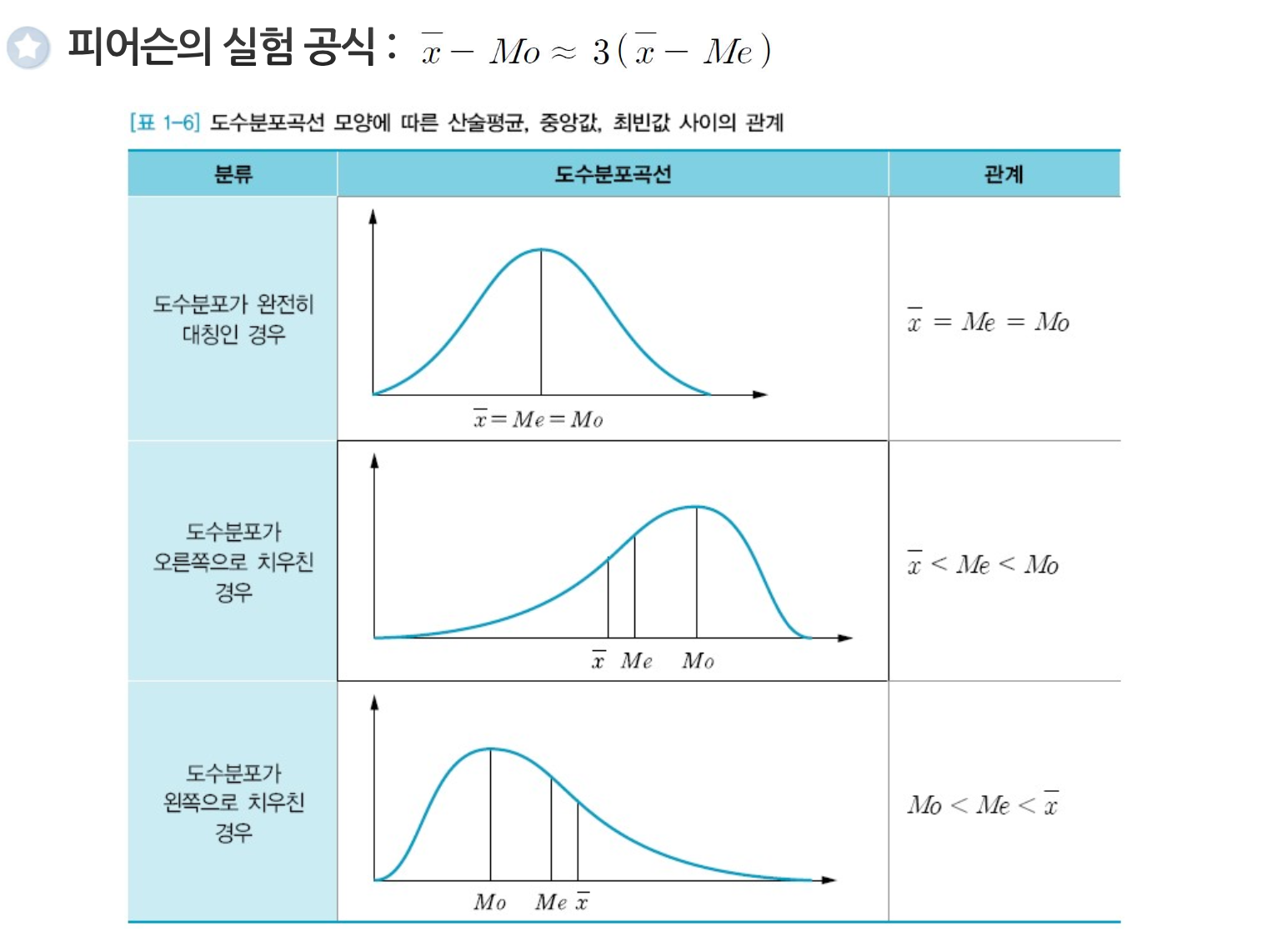
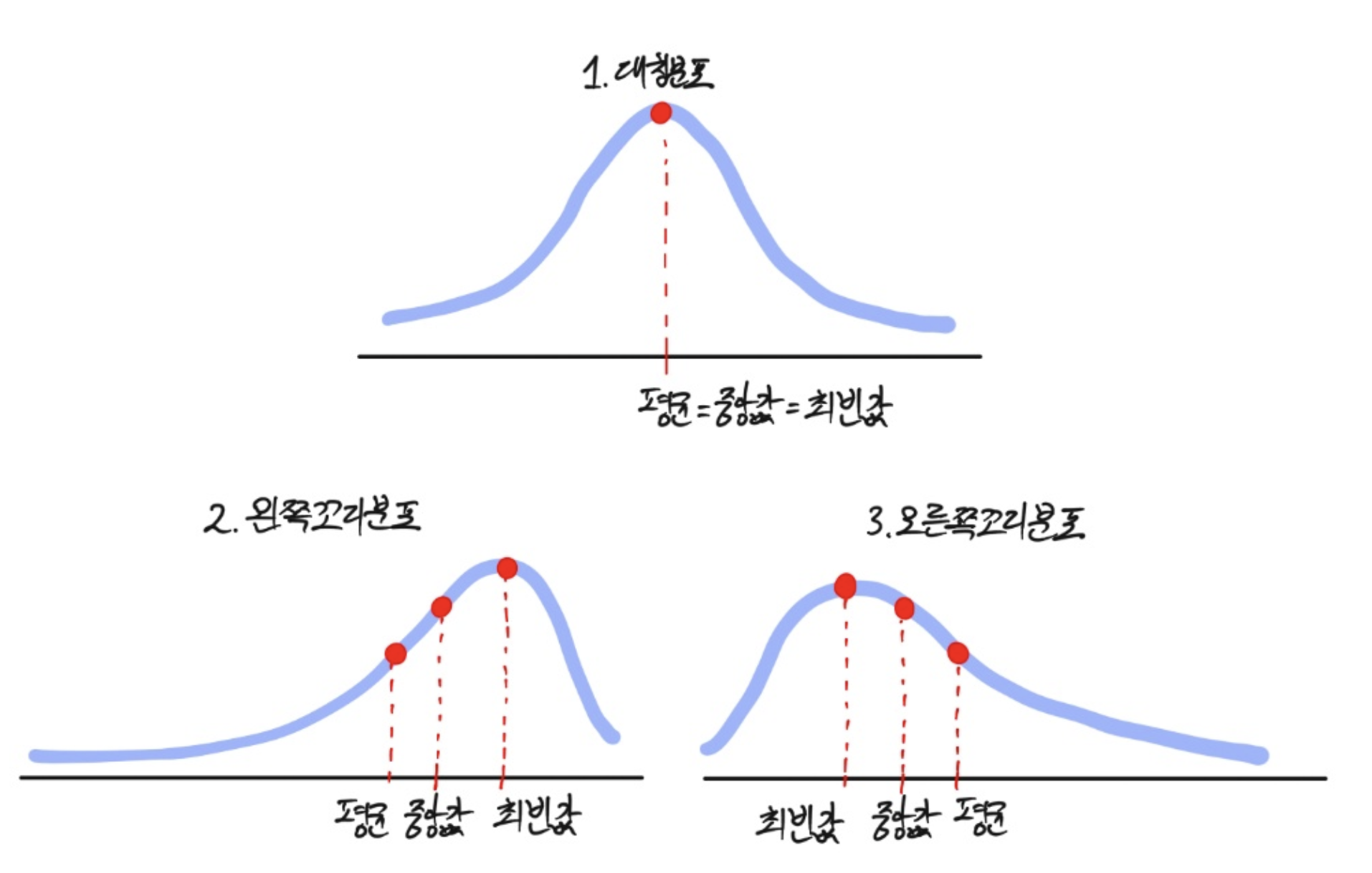
산술평균,중앙값, 최빈값 사이의 관계
Me중앙값
Mo최빈값
Excel
n수 COUNT
표본평균 AVERAGE
중앙값 MEDIAN
최빈값 MODE
백분위수와 사분위수
-
백분위수
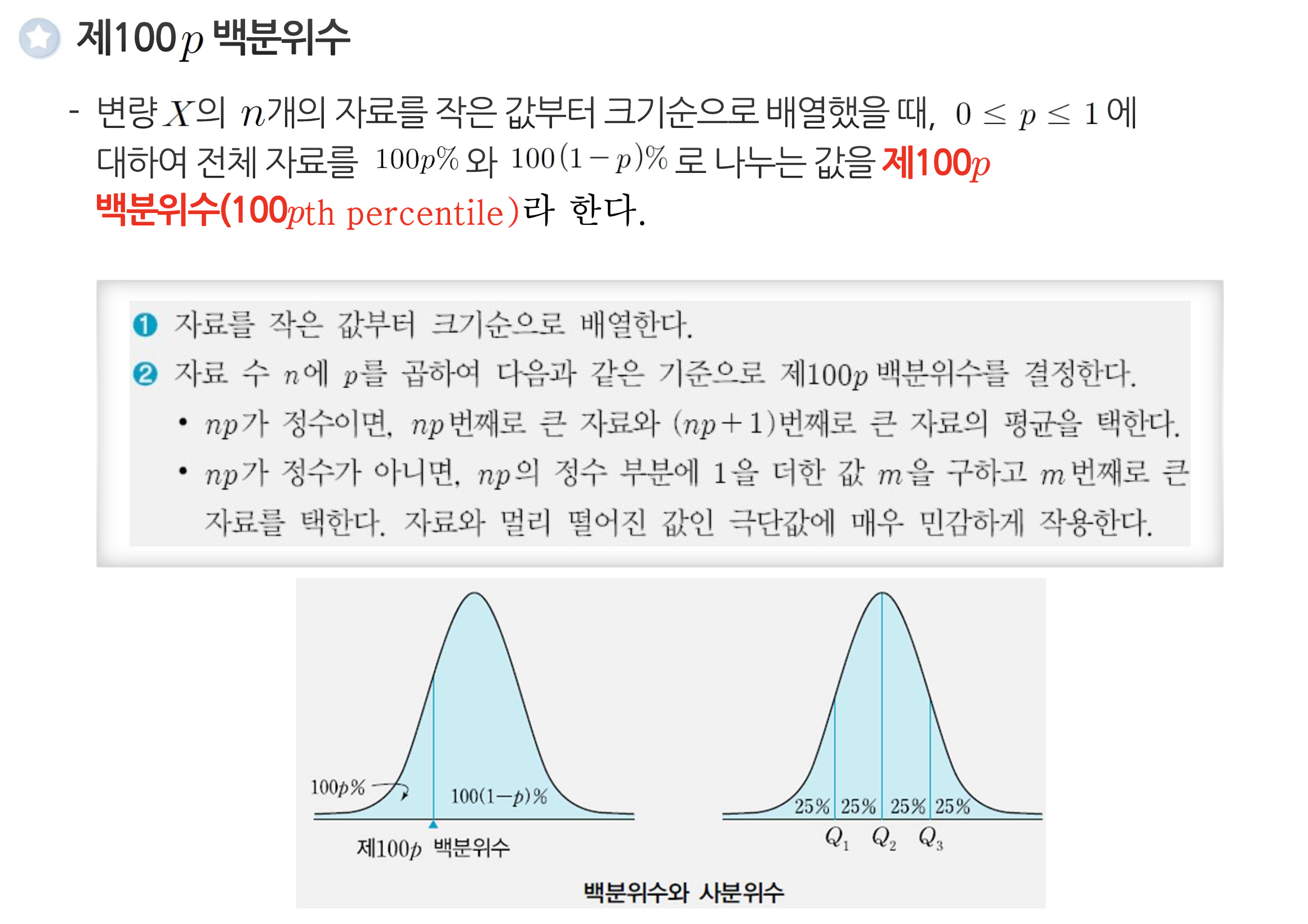
-
사분위수
제 25,50, 75백분위수는 자료를 4등분하는 위치에 있는 값으로, 이값은 사분위수(quartile)이라고 한다.
이를 각각 Q1,Q2,Q3로 표시하며, Q1을 제1사분위수, Q2를 제2사분위수(중앙값), Q3를 제3사분위수라고 한다.
절사평균
평균의 장점과 중앙값의 장점으로 모두 고려한 대표값으로 극단값을 제외하고 구한 평균
- 절사평균을 계산하려면 절사비율(%)절을 결정해야 하는데, 절사비율은 전체 데이터 개수에 대하여 상위 몇 퍼센트의 데이터와 하위 몇 퍼센트의 데이터를 배제할 것인가로 결정한다.

Excel
(QUARTILE.INC : 사분위수 계산)
(PERCENTILE.INC : 백분위수 계산)
산포도:자료의 흩어진 정도
범위
최댓값-최소값
사분위수 범위 ( IQR ):전체 자료의 50%
제 1사분위 수와 제 3사분위수 사이의 거리
Q3 - Q1 으로 나타납니다.

분산과 표준편차
분산(variance)
평균을 중심으로 각 변량이 흩어진 정도를 알기 위하여 각 편차의 제곱의 합을 변량의 개수로 나눈 값, 즉 편차의 제곱의 평균

표준편차:분사의 양의 제곱근

-X의 자료가 도수분포표로 주어질 때의 표준편차는 다음과 같다.

Excel
(VAR.S : 분산)
(STDEV.S : 표준편차)
-모분산은 n으로 나누는데, 왜 표본분산은 n-1로 나누어 계산하나요?
표본분산의 분모를 작게만들어 전체 표본분산을 크게 만들었다.
변동계수
-평균을 중심으로 상대적으로 흩어진 정도를 측정하는 척도

*측정 단위가 동일하지만 평균이 큰 차이로 다른 두 자료 집단 또는 측정 단위가 서로 다른 두 자료집단에 대한 산포도의 척도로 사용하는 것은 바람직하지 않다.
⭐️5점요약표시
최소값, 제1사분위수, 중앙값, 제3사분위수, 최대값
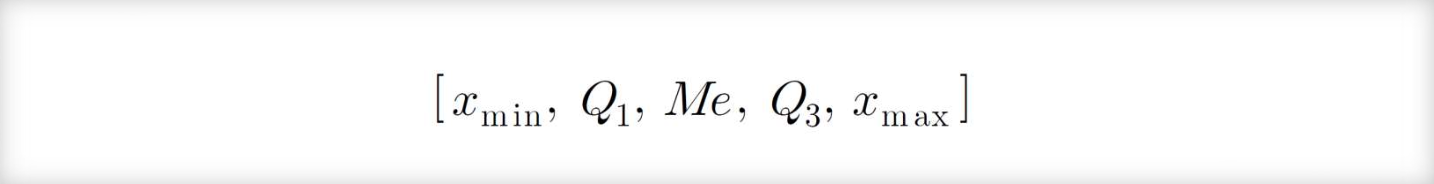
*시험!! 해석: 평균보다 낮은 값인가,이상치랑 놓고 비교
Excel
(INC : include-QUARTILE.INC는 경계값을 포함하여 사분위를 구한다)
(EXC : exclude-QUARTILE.EXC는 경계값을 포함하지 않고 사분위를 구한다는 것)
경계값(MIN, MAX)
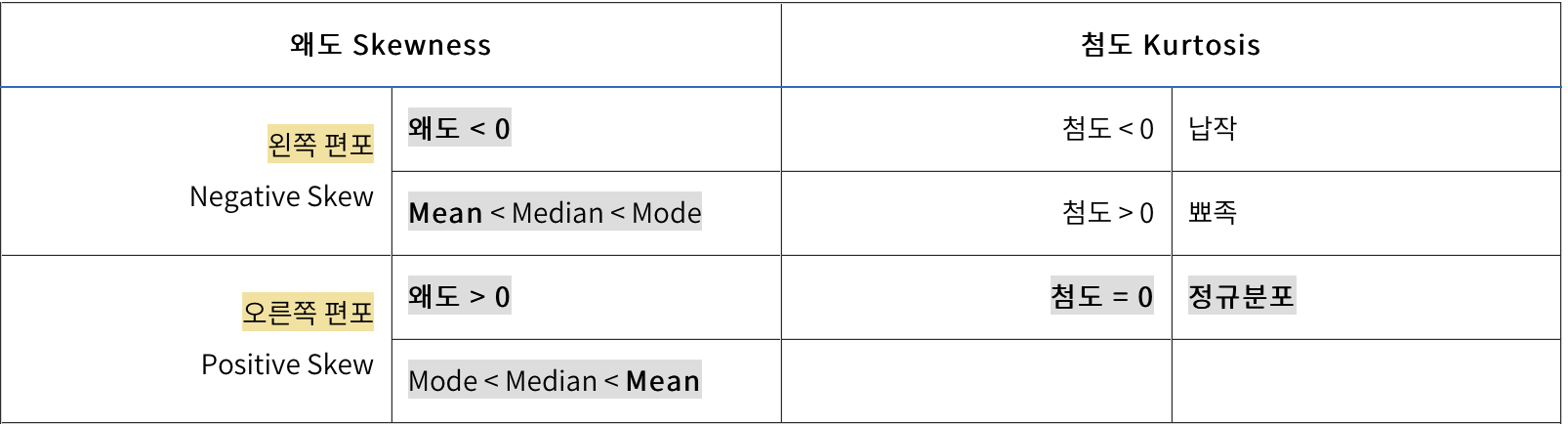
왜도 (비대칭도)/3차적률/0
-분포의 대칭이나 비대칭의 정도를 표시하는 척도

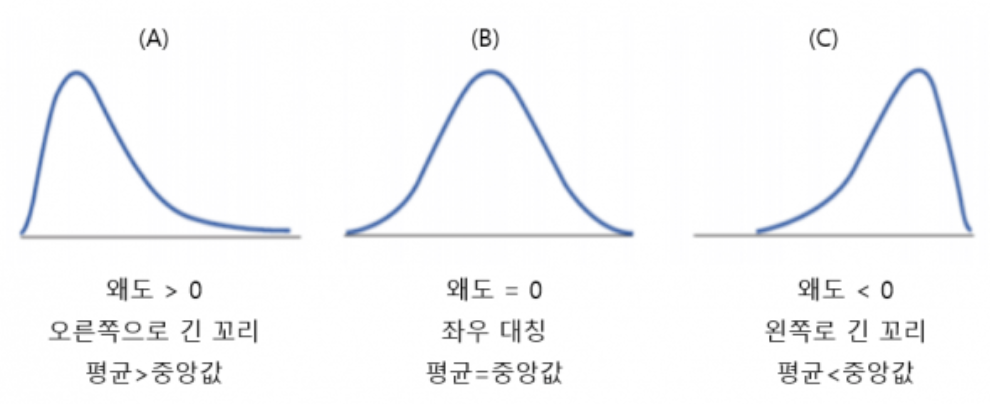
α=0이면 대칭분포이다.
α>0이면 왼쪽으로 치우친 분포이다.
α<0이면 오른쪽으로 치우친 분포이다.
첨도/4차적률/3
-뽀족함의 정도를 나타내는 척도

β=3이면 뽀족한 정도가 표준정규분포와 같다.
β>3이면 표준정규분포보다 정점이 높고 뽀족하다.
β<3이면 표준정규분포보다 정점이 낮고 완만하다.
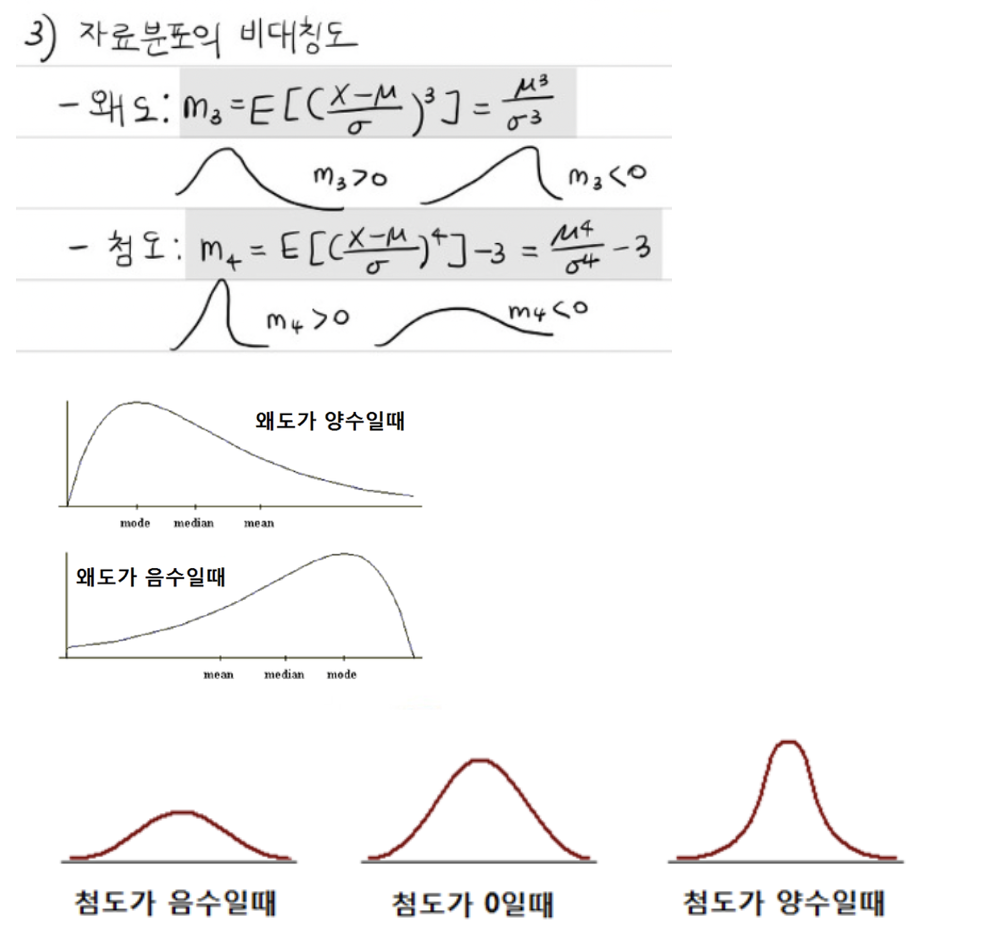
*E-17:마이너스 17승 10^-17
Excel
(SKEW(범위) : 왜도)
(KURT(범위) : 첨도)
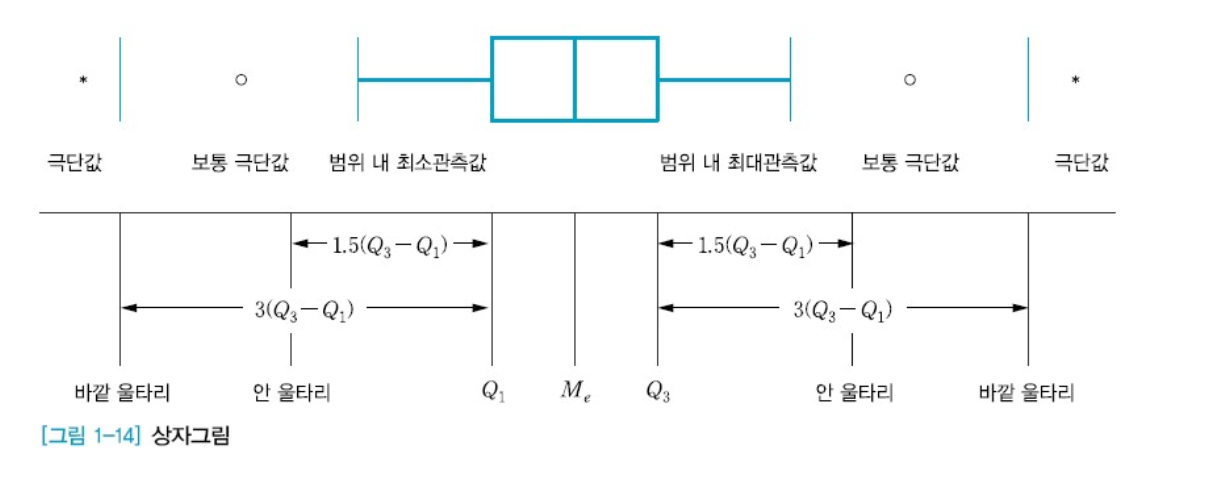
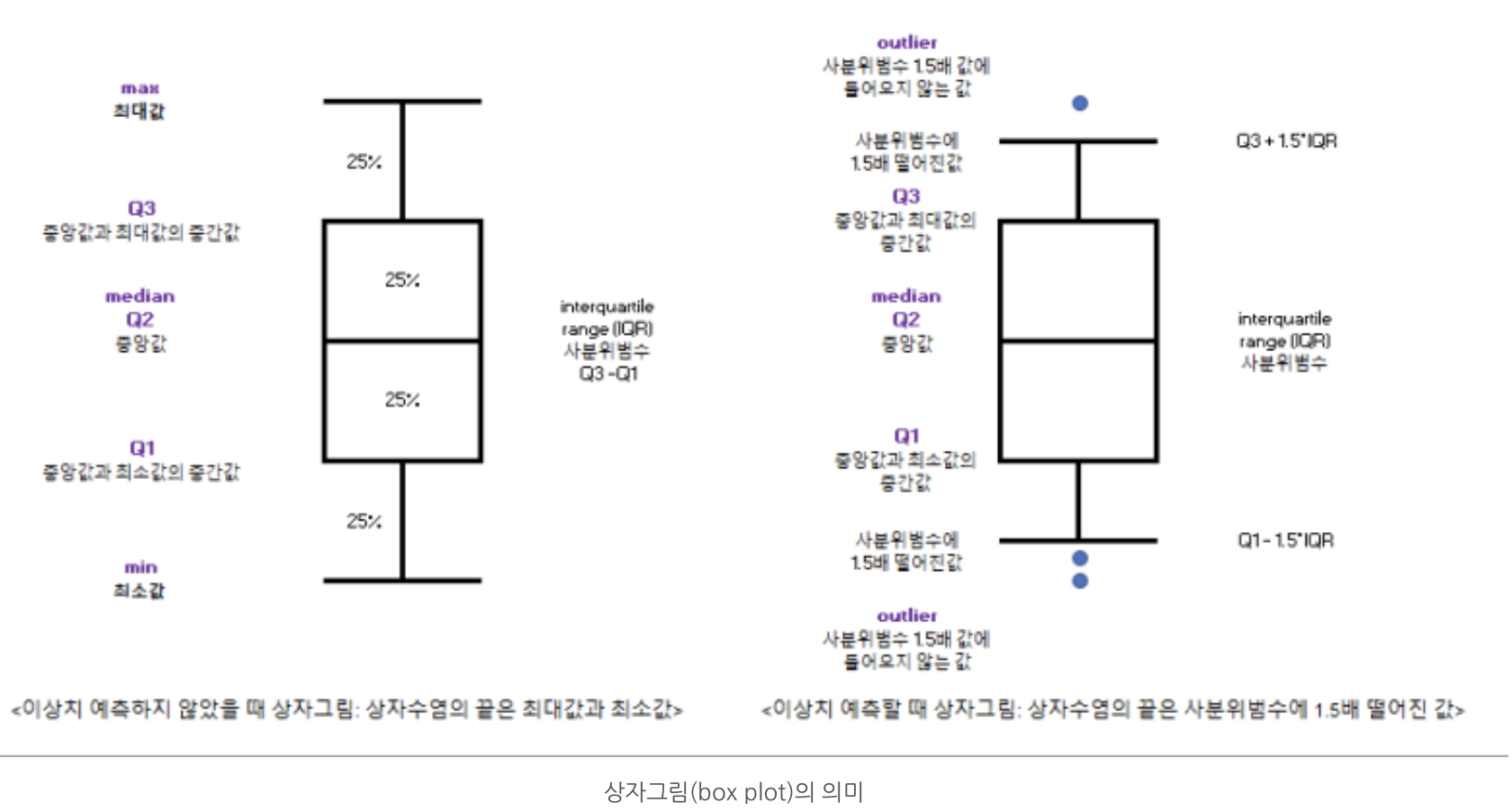
상자그림
⭐️극단값, 바깥울타리 시험
분포의 대칭성, 자료의 중심 위치, 산포도(또는 흩어진 정도),
분포의 꼬리 부분에서의 집중 정도 등을 파악하는데 상자그림(box plot)이 필요하다.

⭐️시험 이상치 나옴