분류 회귀 트리

■ 가장 명료하며 결과에 대한 해석이 용이
■ 관측지들을 하위 그룹으로 분리해 나가는 절차의 반복
■ 하위 그룹으로의 분활 작업 ➔ 예측 변수 기반
■ 재귀적 분활(Recursive partitioning)&가지치기(Pruning)
■ 모델 생성 이후 대량의 표본을 처리하는 계산 용이함

트리 구조

기본 구조
■ 결정 노드 (Decision node) : 자식 노드를 가짐. 예측 변수 값만 알고 있는 새로운 관측치를 분류하기 위해 트리 모델을 사용할 경우 관측치를 트리에 떨어져서 적합한 값을 갖는 가지를 통해 트리 아래로 내려 보냄
■ 단말 노드 (Terminal node) : 자식이 없는 노드. 예측 변수에 의한 데이터의 분할

의사결정 규칙
■ 트리가 적절하다면 모델이 제공하는 결정 기준이 이해하기 쉬움
■ 분할 노드의 상단 조건 : 분할을 위해 예측값 & 분할값 제공 (예. 상위 노드의 소득 <= 110.5)
■ Sample : 해당 노드의 레코드 수
■ Values : 해당 노드에 있는 클래스 개수

■ 새로운 관측치의 분류
▪ 관측치를 트리 모델의 위에서 아래로 할당하는 과정
▪ 새로운 관측치의 클래스는 투표를 통해 결정

■ 재귀적 분할
▪ 종속 변수 : Y, 예측 변수 : X1, X2, ..., Xn
▪ 분류 문제è모델의 결과 변수가 범주형 변수
▪ 예측 변수들의 p차원 공간을 서로 겹치지 않는 다차원의 직사각형으로 분할
1. 하나의 변수 Xi가 선택되고 p차원의 공간을 두 부분으로 분할하게끔 Xi의 변수 값인 Si가 선택
2. 이 중 한 부분은 Xi ≤Si 인모든점을포함
3. 나누어진두부분중한부분은마찬가지로동일한과정에의해다시한번변수를선정 4. 위의 과정을 반복

분류 트리

■ 재귀적 분할
▪ 종속 변수 : Y, 예측 변수 : X1, X2, ..., Xn
▪ 분류 문제è모델의 결과 변수가 범주형 변수
▪ 예측 변수들의 p차원 공간을 서로 겹치지 않는 다차원의 직사각형으로 분할
1. 하나의 변수 Xi가 선택되고 p차원의 공간을 두 부분으로 분할하게끔 Xi의 변수 값인 Si가 선택
2. 이 중 한 부분은 Xi ≤Si 인모든점을포함
3. 나누어진두부분중한부분은마찬가지로동일한과정에의해다시한번변수를선정
4. 위의 과정을 반복

■ 불순도 측정
▪ 지니 지수 (Gini index)& 엔트로피 측도 (Entropy measure)

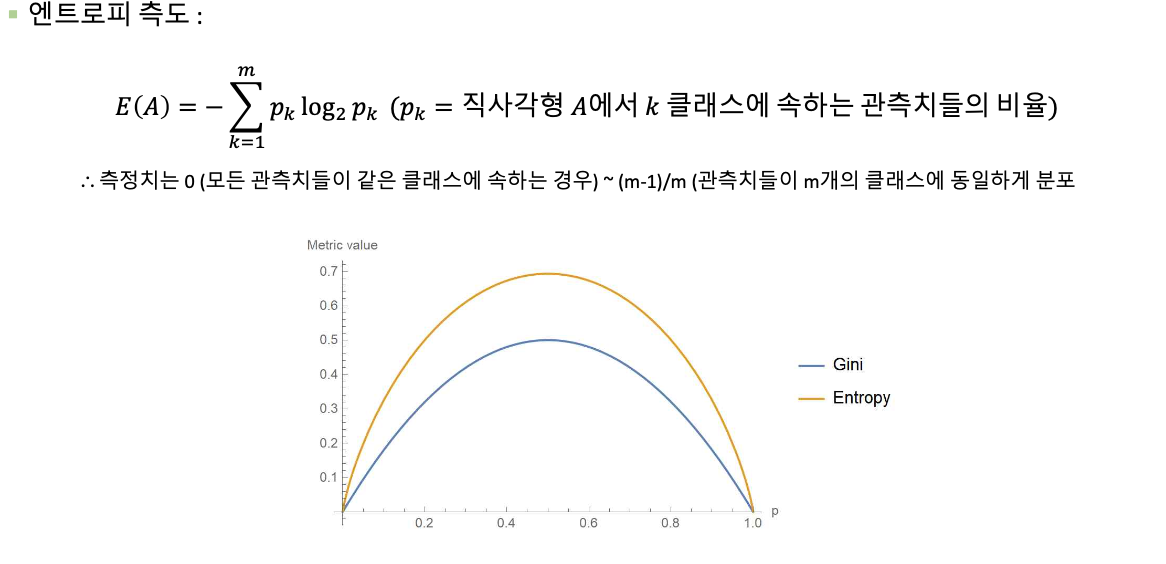
■ 성능 평가
▪ 모델을 평가하고 조정하려면 학습 데이터 셋 외에 표본 데이터가 필요함
▪ 트리 구조는 선택된 표본에 따라서 불안정
▪ 완전 적합된 트리 모델은 과적합(over-fitting) 이슈 존재

■ 과적합 방지

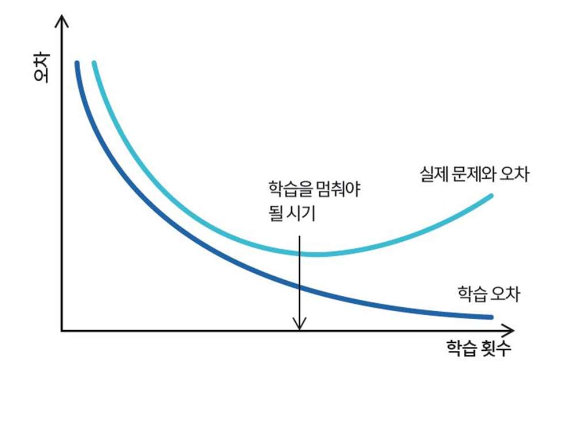
■ 트리 모델 성장 중단
▪ 과적합 되기 전 성장 중단
▪ 범용적 기준 : 트리 모델의 깊이, 노드의 최소 관측치 수, 불순도의 최소 감소량 등

Grid Search

▪ 어떻게 성장을 멈출 것인가? 가장 좋은 타이밍은 언제인가? Grid Search
▪ 파라미터 최적 조합 : 최대 깊이[1,30], 단말 노드의 최소 레코드 수[20,100], 불순도 기준[0.001,0.01]
▪ Grid Search는 각각의 데이터 셋(학습/검증)에 대해 과적합 이슈가 발생할 가능성
▪ 학습 데이터셋에서 CV 수행 ➜ Best model 선정 ➜ 해당 모델에 대해 새로운 검증 데이터 셋으로 평가

■ 트리 모델을 활용하여 연속형 반응 변수 예측
▪ 분류 문제와 본질적으로 같음
▪ 분할이 시도되고 결과로 나온 트리 모델들의 모든 가지에 대해 불순도 측정
➜ 다음 단계에서 불순도의 합이 최소가 되는 분할을 선택

트리 모델 발전
⭐️■ 앙상블 (Ensemble)
▪ 여러 머신러닝 모델을 조합하여 강력한 모델 디자인
▪ 의사 결정 트리 ➜ 랜덤 포레스트 (Random Forest) ➜ 그래디언트 부스팅 (Gradient Boosting)

■ 랜덤 포레스트
▪ 훈련 데이터에 과적합 되는 의사 결정 트리
▪ Bagging의 특별한 경우. 다중 분류/예측 알고리즘을 조합하여 예측 성능 향상

랜덤 포레스트
■ Procedure
▪ 복원 추출 방식으로 데이터로부터 여러 랜덤 표본을 생성 (Bootstrap)
▪ 각 단계마다 랜덤으로 예측 변수들을 선택하여 서브셋 생성 ➜ 표본에 대해 분류 트리 적합
▪ 예측을 향상시키기 위해서 각 트리로부터 얻은 예측/분류 결과를 결합
▪ 분류 ➜ 투표(voting) & 예측 ➜ 평균화(Averaging)

부스트 트리
■ Procedure
▪ 부스트 트리에서는 트리들이 순차적으로 구성 ➜ 각 트리는 이전 트리의 오분류 레코드 고려
1. 단일트리생성
2. 잘못분류된레코드들에가장높은선택확률을제공하는하나의표본추출 3. 새로운 표본을 트리에 학습
4. 단계 2&3을 반복
5. 레코드들을 분류하기 위해서 가중 투표를 사용
6. 가중치의 크기는 구성되는 트리들의 역순으로 부여

로지스틱 회귀

■ 분류 문제 : 이산적 값 중 하나를 선택하는 모델. ‘분류 모델’이라고 부름

문제점:
❶ f(x)의 값이 1 이상이나 0 이하로 나올 수 있음
❷ 각 feature들이 Y에 영향을 주는 것을 해석하는 문제
❸ 사건의 발생 여부는 이산적인데 실제 수식은 연속적

■ 개념
▪ 이진 분류(binary classification) 문제를 확률로 표현
▪ 어떤 사건이 일어날 확률을 P(X)로 나타내고 일어나지 않을 확률을 1 - P(x)로 나타냄 (0 ≤ P(X) ≤ 1) ▪ 오즈비(odds ratio) : 어떤 사건이 일어날 확률과 일어나지 않을 확률의 비율

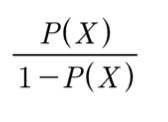
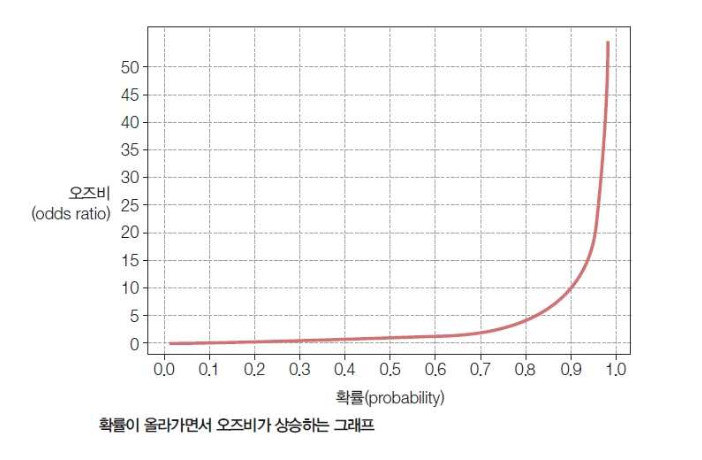
■ Logit Function : 오즈비에 상용로그를 붙인 수식

■ Logistic Function : 로짓 함수의 역함수
그래프가 S자 커브 형태인 sigmoid function

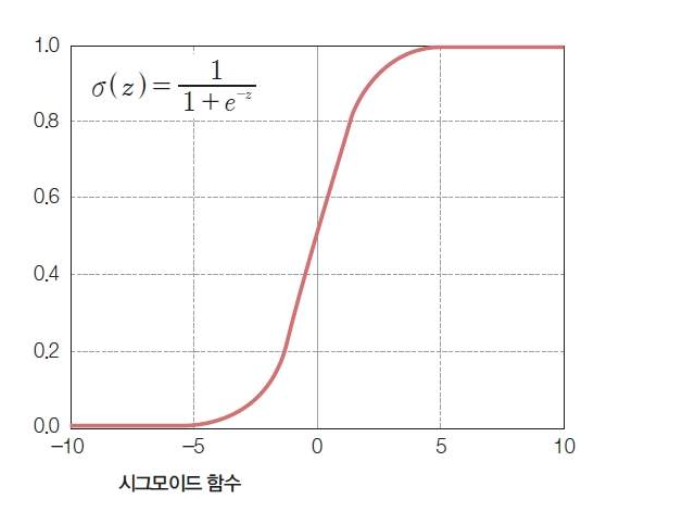
■ Sigmoid Function
▪ y 값을 확률 p로 표현
▪ z 값은 선형회귀와 같이 가중치와 feature의 선형 결합(linear combination)으로 표현 가능

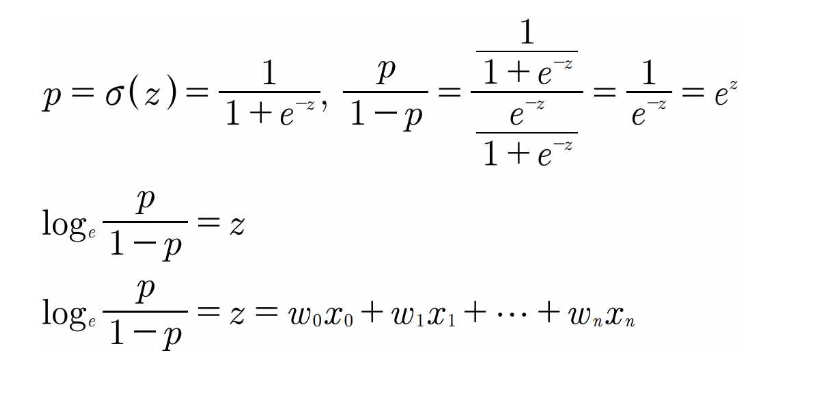
■ Hypothesis Function
▪ z는 가중치 값과 feature 값의 선형 결합

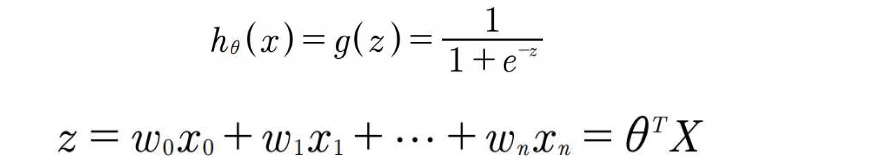
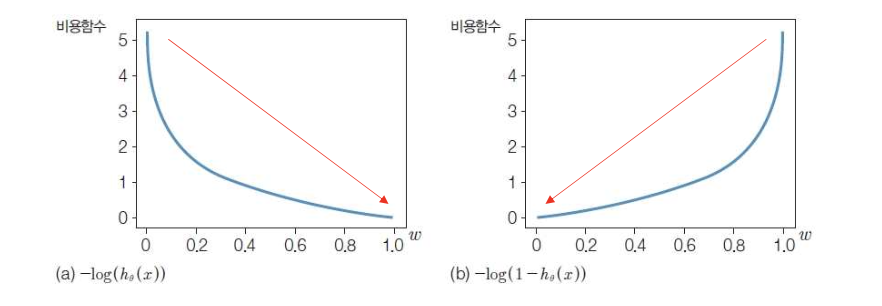
■ Cost Function
▪ 먼저 비용함수를 정의하고 예측값과 실제값 간의 차이를 최소화하는 방향으로 학습
▪ 실제값이 1일 때와 실제값이 0일 때 각각 다르게 비용함수를 정의

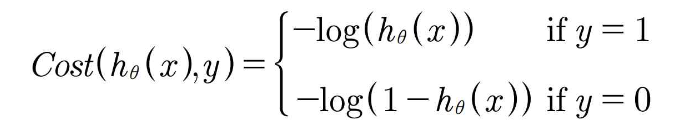
▪ (a)는 y = 1일 때, (b)는 y = 0일 때 비용함수 그래프 (0 ≤ h ≤ 1)

■ 로지스틱 모형
▪ 로지스틱 회귀에서 Y와 β의 관계는 비선형임è최소 제곱법 X
▪ Maximum likelihood : 주어진 데이터를 얻을 가능성을 최대화하는 추정치 찾음. 반복 추정 핵심