
k-NN
요약
■ 분류할 레코드와 다른 모든 레코드 사이의 거리 찾기
■ k-가장 가까운 레코드 선택
▪ 가장 가까운 이웃의 다수결에 따라 분류
▪ 또는 예측을 위해 가장 가까운 이웃의 평균
■ "차원의 저주"- 예측 변수의 수를 제한해야 함
K-NN 분류기(범주형 결과)
■ K-NN모델 중심이 아닌 데이터 중심
■ 데이터에 대한 가정을 하지 않음
■분류하고자 하는 새로운 레코드와 유사한 k개의 이웃 레코드를 식별
■ 이웃 레코드를 사용해 새로운 레코드를 특정 클래스로 분류. 예측 변수 값 X1,X2, ...XP가 유사한 레코드를 의미
x 이웃 레코드들이 속한 클래스들을 참조하여 분류하고자 하는 레코드에 클래스 할당
유클리드 거리
이웃 결정하기
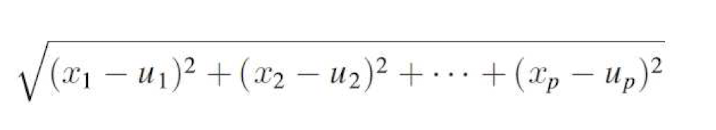
분류규칙
■ 가장 단순한 경우는 k = 1
■ k>1의 이웃을 갖는 경우
▪ 분류될 레코드와 가장 가까운 k개의 이웃
을 찾는다.
▪ 레코드를 분류하기 위해 다수결 결정 규칙을 사용한다. 즉 레코드는 k개 이웃들의 다수가 속하는 클래스로 분류된다.
K값 선택
■ k가 너무 작으면 데이터의 노이즈를 적합할 위험
■ k가 너무 크면 이 알고리즘의 주된 장점 중 하나인 데이터의 지역적 구조를 파악할 수 있는 능력을 놓칠 수 있음
■ 학습 데이터셋을 사용해 검증 데이터셋의 레코드를분류한 다음 다양한 값에 대해 오차율을 계산하여 선택 가장 분류 성능이 좋은 k선택
■ k가 선택되면 새로운 레코드를 분류하기 위해 학습 데이터셋과 데스트 데이터셋을 합치고 알고리즘 반복
컷 오프 값 설정
레코드 분류의 기본: 다수결의 원칙
K-NN 알고리즘의 장점과 단점
■ 장점
▪ 단순하다는 것과 모수에 대한 가정이 거의 없다
▪ 학습 데이터셋이 충분히 많을때, 특히 각 클래스의 특성이 예측 변수 값들의 여러 조합으로 결정될 때 탁월한 성능
■ 단점
▪ 학습 데이터셋으로부터 모수를 추정하는데 걸리는 시간은 없어도 학습 데이터 셋이클 경우에는 근접 이웃을 찾는데 매우 많은 시간이 소요
극복
-주성분 분석과 같은 차원 축소의 방법으로 차원을 감소시킴으로써 거리 계산 시간을 줄인다
-근접 이웃을 빨리 찾기 위해 검색 트리와 같은 저욕한 데이터 구조를 사용한다.
■ 학습 데이터셋으로 필요한 레코드의 개수는 예측 변수의 개수 p가 증가함에 따라 기하급수적으로 증가
■ 많은 학습 시간이 소요되는 계산이 예측에 집중된 '나태 학습 방법Lazy Learner'
Naive Bayes
나이브 베이즈 기본 원리
■ 예측 변수 프로파일이 동일한(즉, 예측 변수 값들이 동일한) 다른 모든 레코드를 찾음
■ 그 레코드들이 어떤 클래스에 속하고 어떤 클래스가 가장 일반적인지 결정
■ 그 클래스를 새로운 레코드의 답
컷오프 확률 방법과 조건부 확률
■ 컷오프 확률
1. 어떤 레코드가 해당 클래스에 속한다고 간주하는 값 이상으로 관심 클래스의 컷오프 확률을 설정
2. 새로운 레코드와 동일한 예측 변수 프로파일을 갖는(즉, 예측 변수 값들이 동일한) 모든 학습 레코드를 찾음.
3. 그 레코드들이 관심 클래스에 속할 확률을 결정
4. 그 확률이 컷오프 확률보다 크면 새로운 레코드의 답을 관심 클래스로 함.
■ 조건부 확률
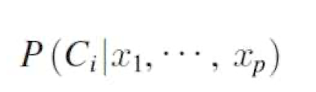
완전한(정확한) 베이지안 분류기의 적용
■ '가장 가능성 있는 클래스에 배정'하는 방법의 사용
■ 컷오프 확률 방법의 사용
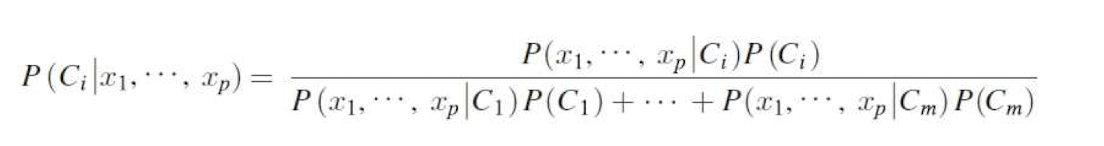
■ 완전한(정확한) 베이즈 절차의 실질적 어려움

