
확률변수
확률분포
기댓값과 분산
결합확률분포
공분산과 상관계수
확률변수
표본공간의 각 원소에 하나의 실숫값을 대응시켜주는 함수
이산확률변수
확률변수 X의 치역이 셀 수 있는 이산값으로 주어지는 확률변수 X
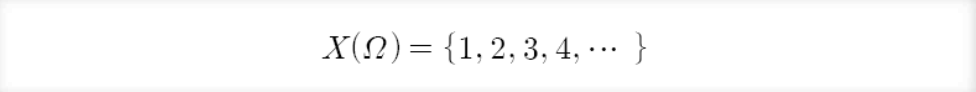
연속확률변수
어떤 연속하는 범위 안에서 모든 실숫값을 가지는 확률변수 X
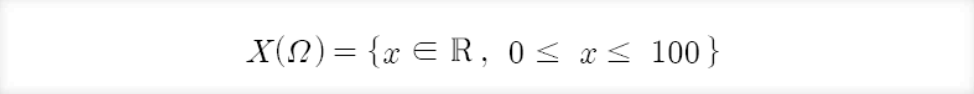
⭐️확률질량함수
이산확률변수 X에 대하여 X가 임이의 실수 x를 취할 확률에 대응하는 다음 함수
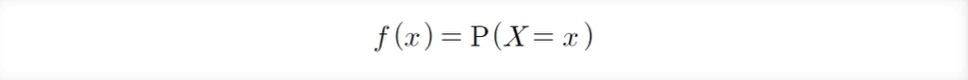
확률질량함수의 성질
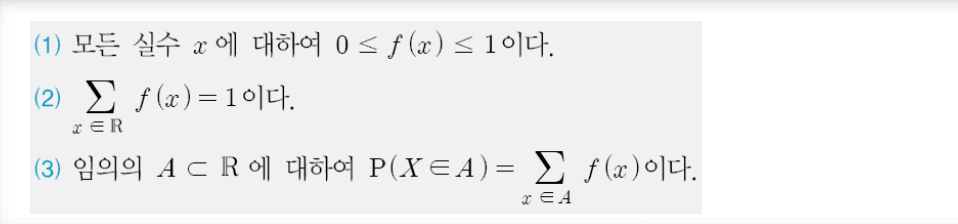
확률밀도함수
연속확률변수 X에 대하여 a<=X<=b일 확률을 다음과 같이 표현할때, 확률변수 X는 연속확률분포를 따른다.
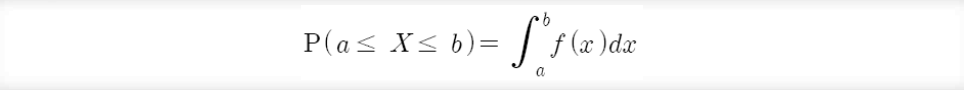
확률밀도함수의 성질

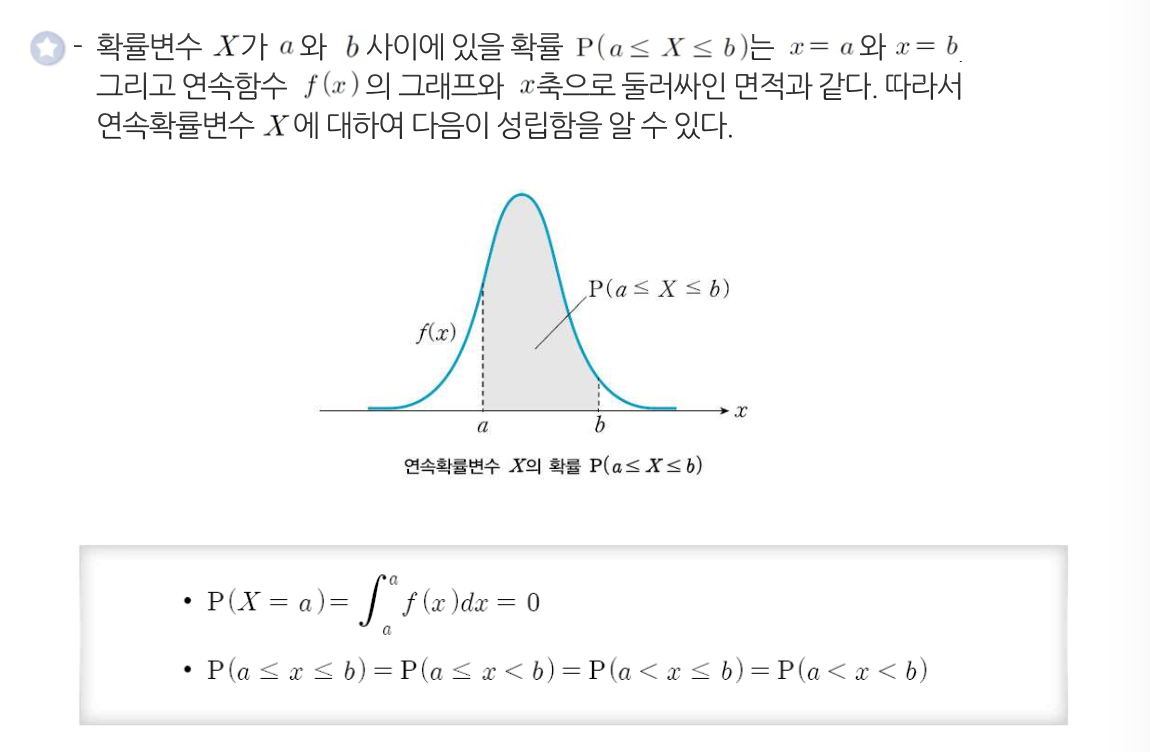
확률분포
이산확률분포
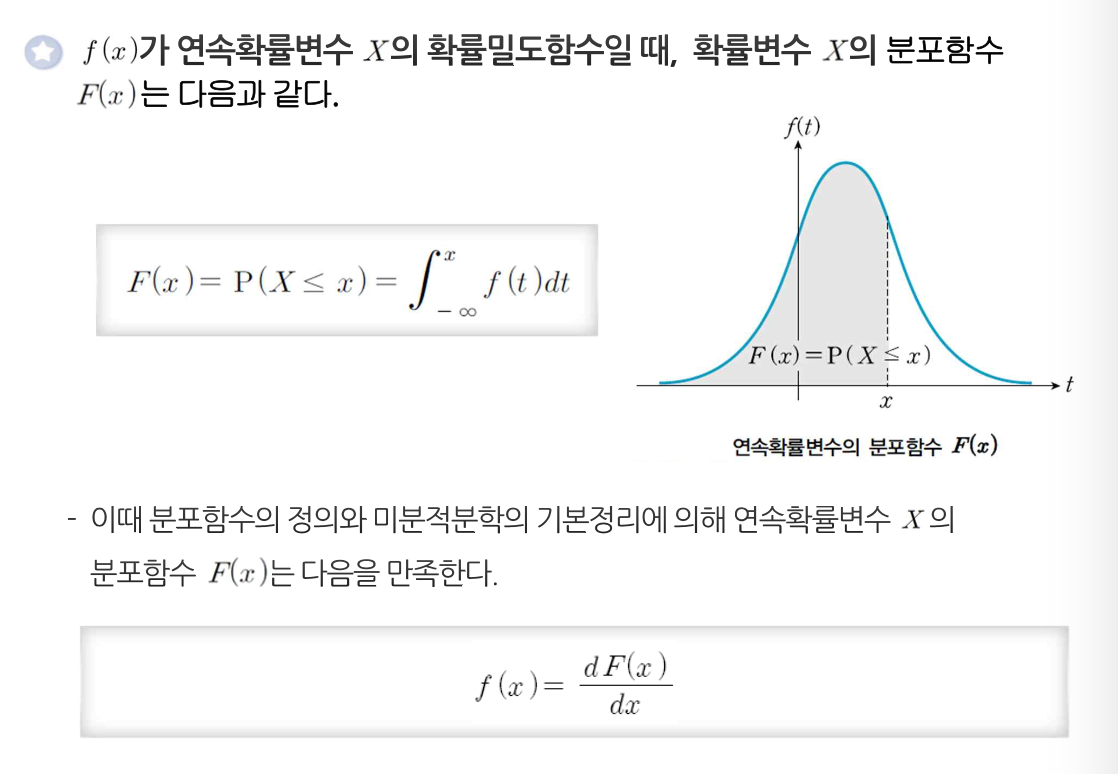
분포함수
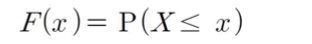
누적분포함수
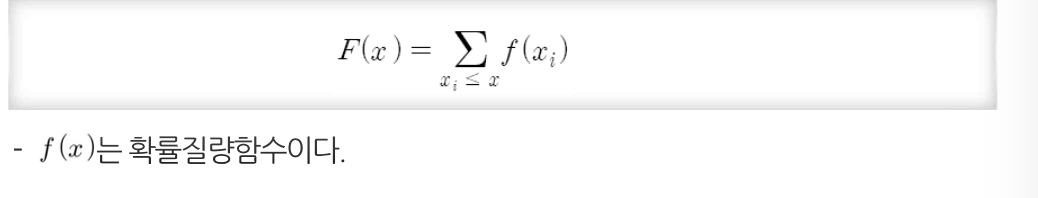
분포함수의 성질

연속확률분포
기댓값과 분산
기댓값


분산

e993b82c0ba8/image.png)
적률생성함수



결합확률분포
결합확률질량함수
정의

함수

성질

결합확률밀도함수
정의

함수

성질




공분산과 상관계수
공분산

즉, 공분산은 X의 편차와 Y의 편차를 곱한것의 평균이라는 뜻이다.
참고자료
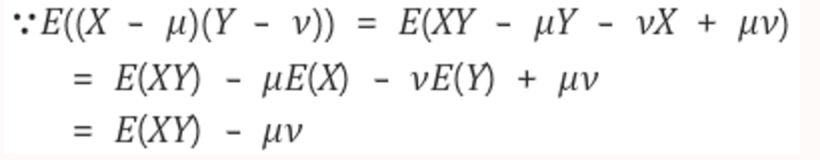
상관계수

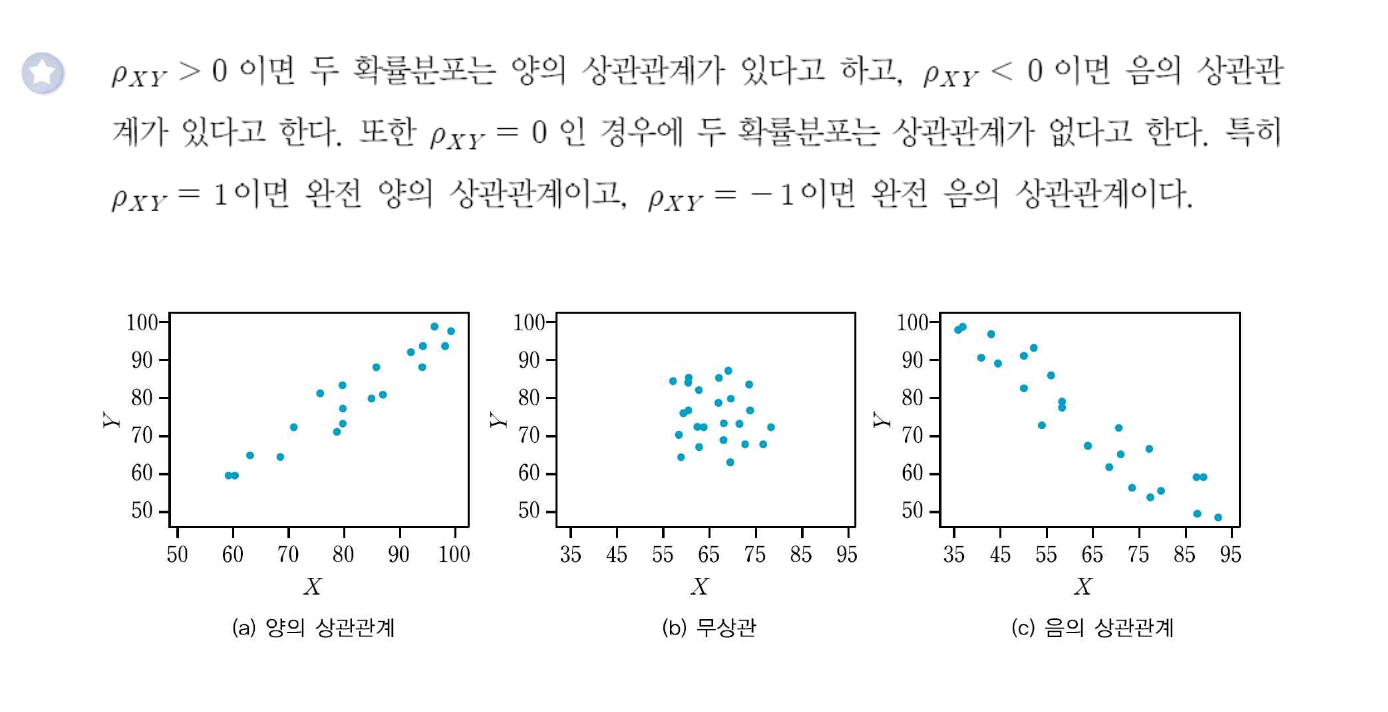
1.상관계수가 1에 가까울수록 두 확률변수는 양의 상관관계를 갖는다.
2.상관계수가 -1에 가까울수록 두 확률변수는 음의 상관관계를 갖는다.
3.상관계수가 0이면 두 확률변수 간에 선형관계가 존재하지 않는다.

상관계수는 공분산을 각각의 확률변수의 분산들의 곱을 제곱근한 것으로 나누어준 것이다. 즉,이 때, 상관계수의 중요한 특징은 반드시 -1에서 1사이의 값을 갖는다는 것이다.