1. 논문 개요(Abstract)

• 제목: RAFT: Recurrent All-Pairs Field Transforms for Optical Flow (link)
• 저자: Zachary Teed(Princeton University) and Jia Deng(Princeton University, Princeton Vision & learning Lab - link)
• 발표지(학회): ECCV2020
• 발표일: 2020
• 개요: 본 논문에서는 optical flow를 계산하기 위한 새로운 심층 신경망 구조인 All-Pairs Field Transforms(RAFT)를 제안한다. RAFT는 각 픽셀마다 feature를 추출하고, optical flow를 이루는 두 이미지간 픽셀 쌍에 대해서 multi-scale 4D corrlation volumes을 만든 후, recurrent unit을 통해 반복적으로 업데이트한다. KITTI 등 유명 공개 데이터셋에서 SOTA를 달성하였고, 모델의 일반화 성능이 좋아 합성데이터셋에서 학습된 모델이 KITTI 등 실세계 데이터에서도 높은 성능을 유지하였다. 또한 1088x436 사이즈 영상에서 Nvidia 1080ti GPU로 초당 10프레임의 처리 속도를 달성하였다.

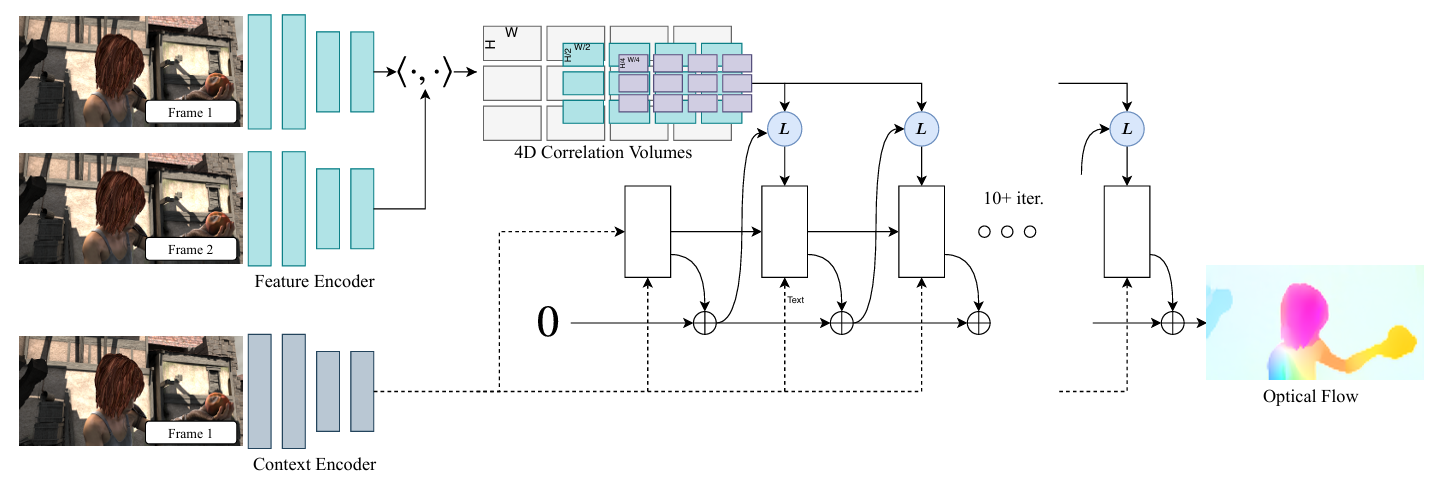
그림 1. RAFT 파이프라인

2. 내용(Methods)

- Setup

• 연속된 두 RGB 이미지 $I_1, I_2$를 입력받아 dense displacement field $(\mathbf{f}^1, \mathbf{f}^2)$를 계산하는 것이 목표
• Dense displacement field $(\mathbf{f}^1, \mathbf{f}^2)$는 $I_1$상의 각 픽셀 $(u,v)$를 $(u',v')=(u+f^1(u), v+f^2(v))$와 같이 매핑함
• 전체 파이프라인은 <그림 1>과 같으며, feature extraction, computing visual similarity, iterative update와 같이 세 부분으로 나눌 수 있고, end-to-end 학습을 위해 모두 미분 가능한 형태로 이루어져 있음

- Feature Extraction

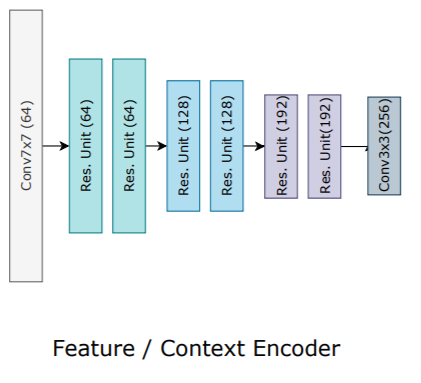
그림 2. Feature extraction network/context network 구조

• 두 입력 이미지의 특징을 추출하기 위해 일반적인 CNN 구조의 네트워크를 활용

• Feature extraction network는 $g_\theta$로 표기하며, $g_\theta : \mathbb{R}^{H \times W \times 3} \rightarrow \mathbb{R}^{H/8 \times W/8 \times D}$와 같이 1/8 해상도록 줄임(D=256)

• Context network는 입력 영상의 context를 RAFT 뒷 단의 reccurent unit에 전달하기 위한 네트워크이며, feature extraction network와 같은 구조를 가지고 있음

- Computing Visual Similarity

그림 3. Correlation volume 구조

Correlation Volume

• $I_1$의 feature vector($g_\theta$를 통해 추출된 feature map 상의 cell)과 $I_2$의 feature vector 사이의 조합 가능한 모든 feature vector 쌍에 대한 correlation을 4D 형태로 계산

• 입력 이미지에 대해서 $g_\theta(I_1) \in \mathbb{R}^{H \times W \times D}$, $g_\theta(I_2) \in \mathbb{R}^{H \times W \times D}$라고 할 때, 다음과 같이 correlation volume을 계산(FlowNet에서 먼저 correlation volume 활용을 제안하였고, RAFT에서는 개념은 같지만 형태가 약간 변경된 형태를 사용)

• 즉, 위의 수식은 이미지 $I_1$의 feature vector $(i,j)$와 이미지 $I_2$의 feature vector $(k,l)$ 사이의 correlation은 $C_{ijkl}$라는 것을 의미하며, 한 번의 행렬곱(각 feature vector 간 내적)으로 계산되기 때문에 효율적

• 이후 correlation volume의 마지막 두 차원에 대해서 average pooling을 취하여 $\{ \mathbf{C}^1, \mathbf{C}^2, \mathbf{C}^3, \mathbf{C}^4 \}$와 같이 4-layer pyramid를 구성함

• 각 level의 correlation volume 차원은 다음과 같음

• 이를 통해 크고 작은 여러 움직임에 대응하며, 특히 correlation volume의 앞쪽 두 차원은 유지함으로써 고해상도 정보 또한 유지하여 고속 이동하는 소형 물체에 대해서도 대응할 수 있도록 함

• Correlation volume 계산 과정은 복잡도가 $O(N^2)$이지만, iteration 전에 단 한번 pre-compute되고, 구현이 쉬우며, 최종적으로는 전체 inference time 중 17%정도만 차지하기 때문에 bottleneck 되지는 않음

• 하지만, 저자들은 더욱 효율적인($O(NM)$) 대체 방법을 제시하고 있으며, 혹시 correlation volume 계산이 bottleneck이 되는 경우 대체 방법으로 교체가 가능하다고 함

• 여기서 $g^{(1)}=g_\theta(I_1)$, $g^{(2)}=g_\theta(I_2)$이며, correlation volume pyramid의 level m($C^m$)을 계산하는 과정을 수식으로 나타낸 것으로, average pooling 과정(첫번째 term)이 두번째 term으로 표현될 수 있음을 보임

• 두번째 term을 보면 correlation volume의 각 원소는 $g^{(1)}$과 $2^m \times 2^m$ 커널을 통해 pooling된 $g^{(2)}$ 사이의 내적으로 표현될 수 있기 때문에, 계산이 오래 걸리는 전체 correlation volume pyramid를 pre-compute하는 대신, pooling된 $g^{(2)}$만 pre-compute 해놓고 이후 과정에서 필요한 correlation feature 만 위의 수식으로 계산하여 사용하면 연산량을 절약할 수 있음

Correlation Lookup

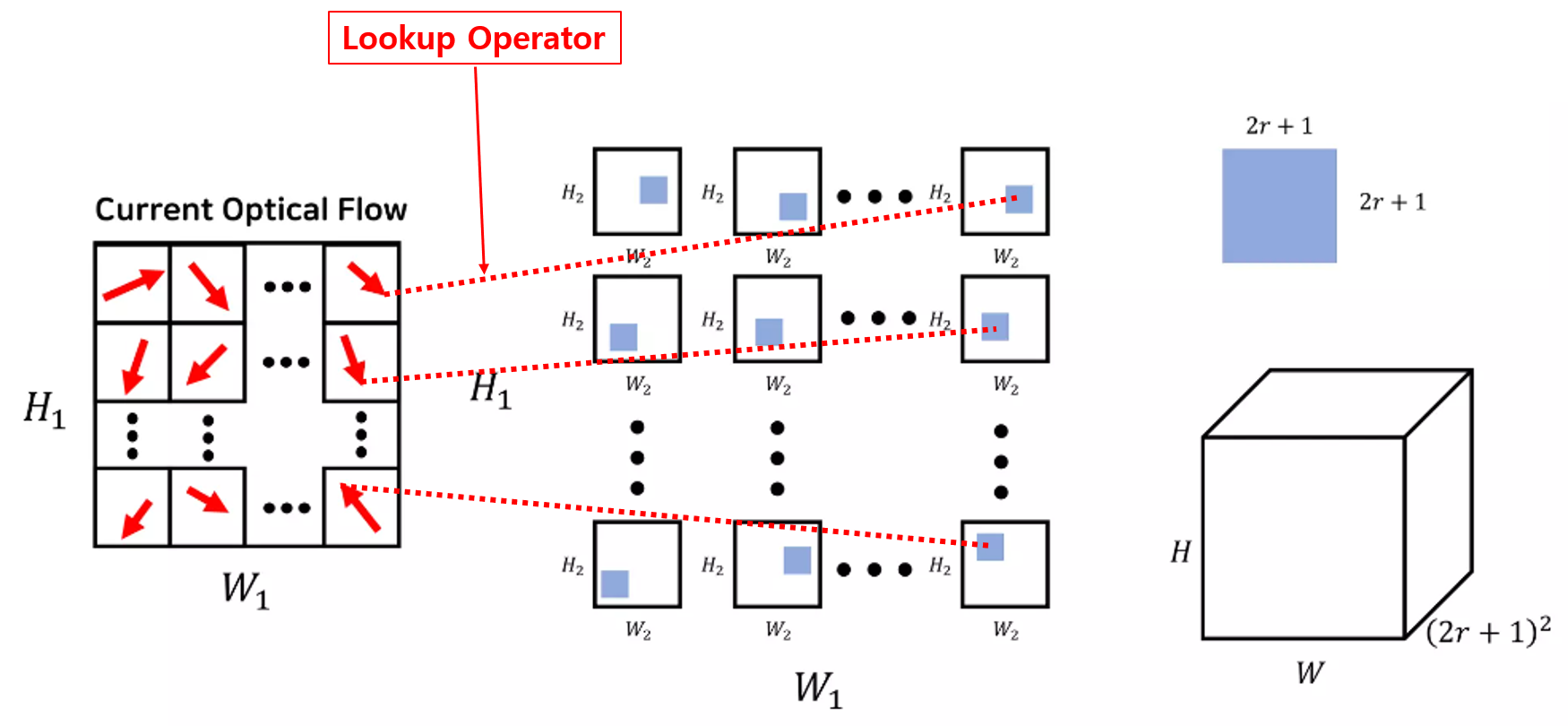
그림 4. Loopup Operator 설명

• 위의 과정에서 계산된 correlation volume pyramid에서 인덱싱을 통해 학습에 필요한 feature map을 생성하는 과정인 lookup operator $L_c$를 정의
• Optical flow $(\mathbf{f}^1, \mathbf{f}^2)$가 주어졌을 때, $I_1$상의 각 픽셀 $\mathbf{x}=(u,v)$는 $\mathbf{x'}=(u+f^1(u), v+f^2(v))$와 같이 매핑됨
• 예측된 optical flow가 올바르다면, $I_1$상의 어떤 target pixel과 주어진 optical flow로 매핑된 $I_2$상의 픽셀간 correlation이 높아야함 (3D 상에서 같은 위치에 존재하는 pixel들이기 때문에)
• 이에 근거하여, RAFT의 이후 업데이트 과정에서 $I_1$상의 target pixel과 주어진 optical flow로 매핑된 $I_2$상의 픽셀간 correlation을 앞에서 계산된 correlation volume pyramid에서 찾아 feature map을 구성하여 활용하고, 이렇게 correlation volume pyramid에서 우리가 원하는 픽셀간 correlation을 찾는 과정이 lookup operator임
• <그림 4>는 이러한 lookup operator의 동작을 보여주며, 아래의 식과 같이 optical flow로 매핑된 $I_2$상의 픽셀 주변 local neighborhood($I_2$상의 매핑점 $\mathbf{x}'$와 L1 길이로 $r$ 이내에 존재하는 지점)의 correlation을 동시에 활용

• 즉, <그림 4>와 같이 $I_1$상의 target pixel(왼쪽 그림의 빨간색 화살표의 시작점)을 예측된 optical flow(화살표)를 이용하여 $I_2$상의 픽셀(화살표의 끝점)에 매핑하고, 그 주변 픽셀들의 correlation 값들(가운데 그림의 파란색 박스, 총 $(2r+1)^2$개의 correlation 값)을 하나의 차원으로 concat하여 오른쪽 아래 그림과 같은 feature map(픽셀 하나당 $(2r+1)^2$개의 correlation 값이 생성되어 최종적으로 $H \times W \times (2r+1)^2$ 크기)을 생성
• 이때, optical flow는 실수이고, 이미지 pixel의 좌표는 discrete하므로 optical flow로 매핑된 위치에 대한 값을 bilinear sampling을 통해 계산
• 모든 pyramid level에 대해 같은 lookup 연산을 수행하며, 즉, level k에서는 $\mathcal{N}(\mathbf{x}'/2^k)_r$의 grid를 사용해 indexing이 수행됨.
• 또한 모든 pyramid level에 대해 같은 radius를 적용하여, 낮은 level에서는 더 넓은 영역의 context 정보를 포함하게 됨(예를 들어 가장 낮은 level인 k=4의 경우, r=4가 256 픽셀 영역에 대응됨) (논문에서는 radius라고 표현하기도 했고, 수식에서도 L1 거리로 $r$이내의 correlation 값들을 활용하는 것으로 나와서 논문만 읽었을 때는 <그림 4>의 $(2r+1)^2$ 사각형 모양이 아닌 원 영역의 correlation 값들을 활용하는 것으로 보였는데, 코드에서 $(2r+1)^2$ 크기를 사용)
• 각 pyramid level에서 추출된 feature map은 하나의 tensor로 concatenate됨

- Iterative Updates and Training

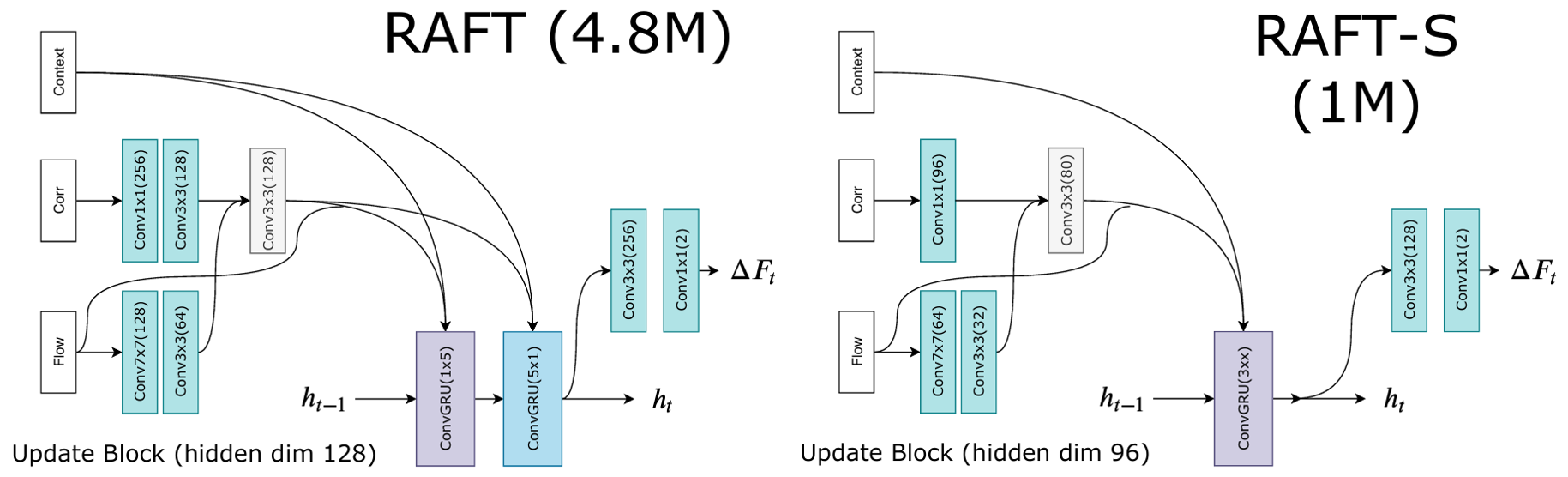
그림 5. Update Operator 구조

• 입력 데이터 $x_t$는 예측된 optical flow feature, correlation feature, context feature가 concatenate된 데이터

  • Optical flow feature는 이전 step에서 예측된 optical flow 결과에 두 개의 convolutional layer를 적용하여 추출된 feature
  • Correlation feature는 위의 lookup 연산을 통해 생성된 feature map에 두 개의 convolutional layer를 적용하여 추출된 feature(논문에서는 이렇게 말하고 있는데 그림에는 optical flow feature 정보를 concat하여 convolutional layer를 한 번 더 거치는 것으로 표현됨. 코드 확인해 보니 그림처럼 concat 수행.)
  • Context feature는 context network의 출력값을 그대로 사용

• Update를 수행하는 convGRU는 다음과 같이 구성 ( $z_t$ 등을 계산할 때, $h_{t-1}, x_t$를 concat하고 convolutation 수행) (RNN, LSTM, GRU)

• $3 \times 3$ convolutional layer를 $5 \times 1$ convGRU, $1 \times 5$ convGRU로 분리된 두 개의 GRU로 대체했을 경우 큰 연산량 상승 없이 receptive field를 효과적으로 넓힐 수 있음

• 마지막 GRU cell의 은닉층에 두 개의 convolutional layer를 적용하여 flow update 량, $\Delta \mathbf{f}$를 추정하며, 이를 이용하여 다음과 같이 최종적인 optical flow를 계산 및 업데이트 함

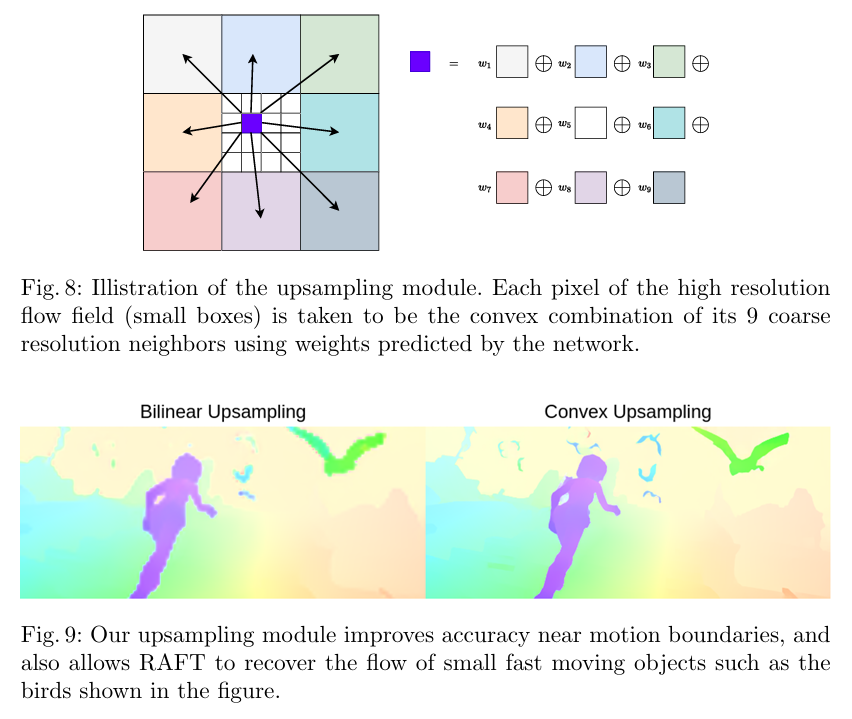
그림 6. Upsampling 방법

• 다만 이렇게 출력된 optical flow는 원본 이미지 해상도 대비 1/8이므로 Upsmapling이 필요하며, 일반적인 bilinear upsampling보다 convex upsampling이 성능이 더욱 좋았다고 함
  • 네트워크 출력은 원본 해상도 대비 1/8 크기이므로, 네트워크 출력(optical flow)의 한 셀은 원본 영상의 8x8 픽셀에 대응됨
  • Upsampling을 통해 원본 영상의 8x8 픽셀 중 하나(<그림 6>의 작은 파란색 박스)의 값을 결정하기 위하여, 해당 픽셀에 대응되는 네트워크 출력(optical flow)의 셀 1개뿐 만 아니라 그 주변 8개의 셀(<그림 6>의 큰 색깔 박스들)까지 총 9개의 optical flow 값을 가중합함
  • 각 가중치 또한 신경망을 통해 결정되며, GRU의 최종 출력층에 optical flow를 결정하는 branch와는 별개로 추가적인 두개의 convolution layer를 적용하여 $H/8 \times W/8 \times (8 \times 8 \times 9)$의 가중치 mask를 계산 (네트워크 출력의 하나에 셀에 대응되는 8x8 픽셀 각각에 대한 9개 optical flow의 가중치)
  • 전체 upsampling 과정은 위와 같이 구한 mask와 Pytorch의 unfold 함수를 통해 구현됨
• 최종적인 loss function은 다음과 같으며, 모든 iteration의 output($\{ \mathbf{f}_{1}, \cdots, \mathbf{f}_{N} \}$)과 ground-truth 간의 L1 거리를 합하여 구성 (실험을 통해 $\gamma = 0.8$로 결정)

3. 실험 결과(Experiments)

• "FlyingChairs"(batchsize 12, 100k iterations), "FlyingThings"(batchsize 6, 100k iterations)라는 합성데이터셋에서 네트워크를 순서대로 pre-train
• 이후 Sintel, KITTI-2015, HD1K 데이터셋에서 100k iteration 만큼 finetuning
• 최종적으로 KITTI-2015에서 50k interation 만큼 finetuning
• 학습시 $\Delta \mathbf{f} + \mathbf{f}_k$에서 $\mathbf{f}_k$ 쪽 branch(이전 step의 GRU cell로 연결됨)는 gradient 전파가 일어나지 않도록 설정

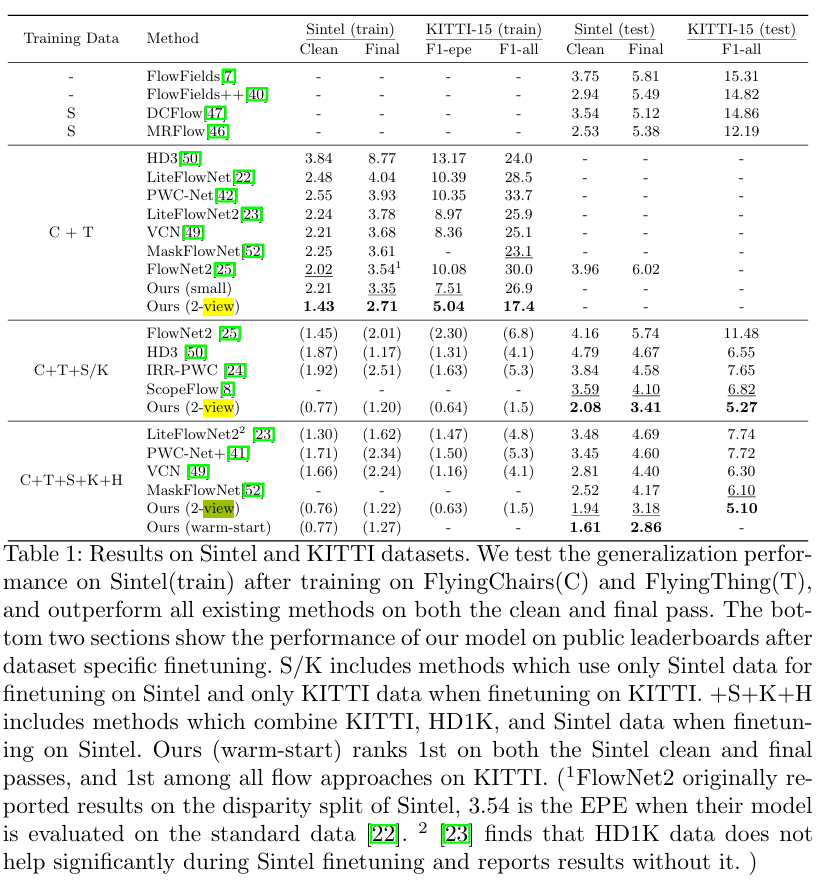
그림 7. 실험결과

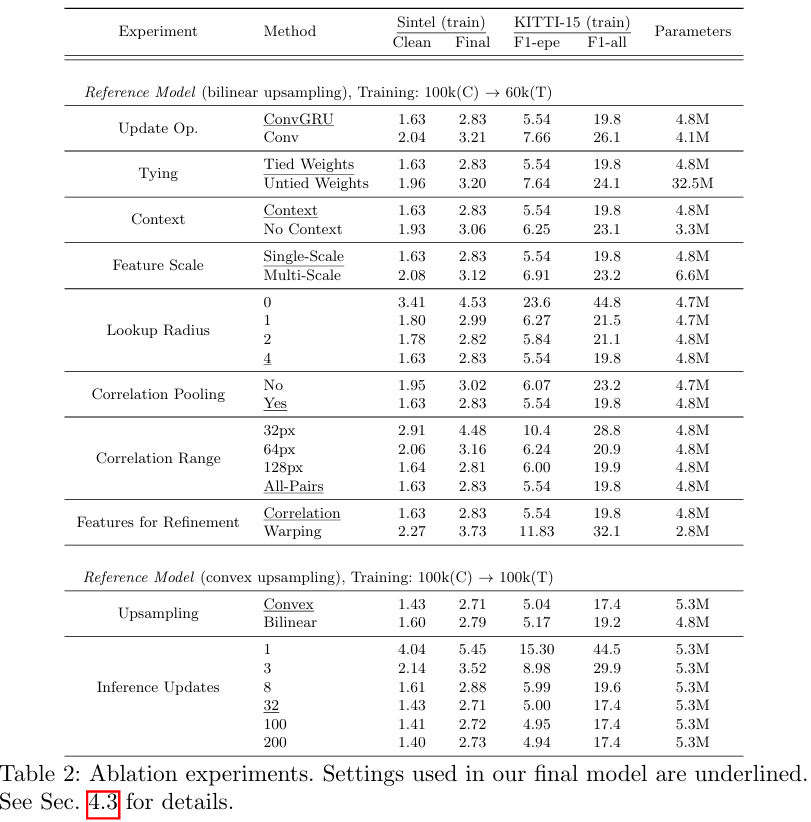
그림 8. Ablation study

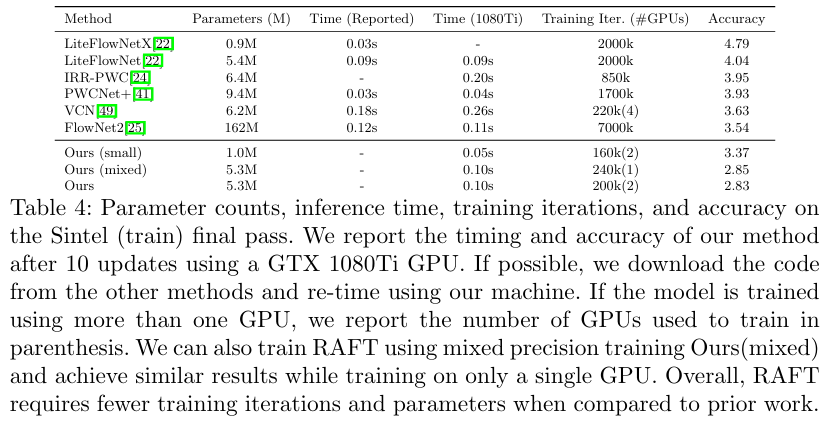
그림 9. 속도 및 네트워크 크기

개인적인 생각

• 해당 연구자의 후속 연구인 DROID-SLAM도 비슷한 구조(GRU를 통한 지속적인 iteration으로 결과를 refine)를 가지고 있고, 해당 연구실의 유명 논문 중 하나인 stacked hourglass network도 이전 step의 keypoint heatmap을 입력받아 같은 네트워크 구조를 iteration하여 결과를 refine하는 구조를 가지고 있는데, 이런 방식이 성능 향상에 도움이 크게 되는 듯

• 또한 본 논문과 DROID-SLAM의 주요 contribution으로 기존 딥러닝 기반 방법의 고질적인 문제인 일반화 성능을 크게 향상시켰다고 명시하고 있는데, iteration을 돌리는 구조 덕분인 것 같음(GT와 유사한 값을 바로 예측하기도 하지만 refinement를 위하여 GT와 이전 step의 차이 값 또한 예측을 하기 때문에 좀 데이터가 증강되는 효과가 있는 것 같기도??)