1. 논문 개요(Abstract)

• 제목: BA-NET: DENSE BUNDLE ADJUSTMENT NETWORKS (Link)

• 저자: Chengzhou Tang(Simon Fraser University), Ping Tan(Simon Fraser University)

• 발표지(학회): ICLR 2019

• 발표일: 2019

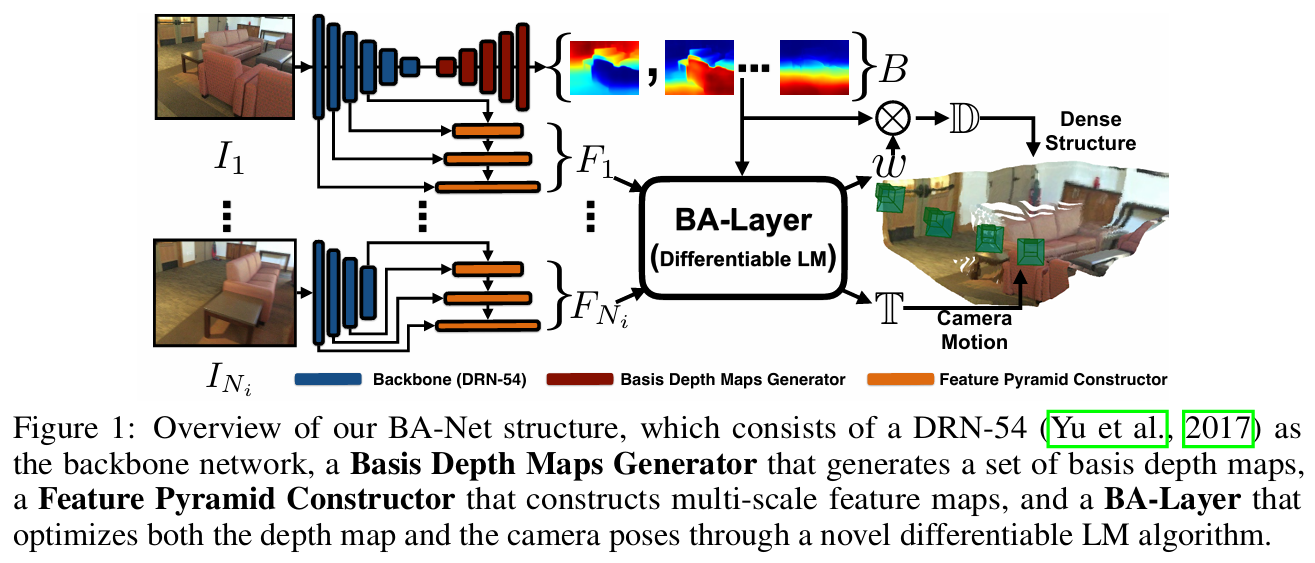
• 개요: 본 논문은 structure-from-motion(SfM) 문제를 해결하기 위해 feature-metric bundle adjustment(BA)를 수행하는 네트워크 구조를 제안하며, 모든 파이프라인이 미분 가능하게 설계되어 네트워크가 BA 문제를 풀기에 알맞는 학습을 할 수 있도록 한다. 또한 본 논문에서는 새로운 depth parameterization 방법을 제시하며, 처음에는 몇 개의 basis depth map을 생성하고, BA 과정을 통해 이러한 basis depth map을 선형 결합하여 최종적인 depth map을 결정한다. BA, depth map 생성은 모두 end-to-end로 학습된다.

그림 1. BA-Net 개요

2. 내용(Methods)

- Feature Extraction and Depth Basis Estimation

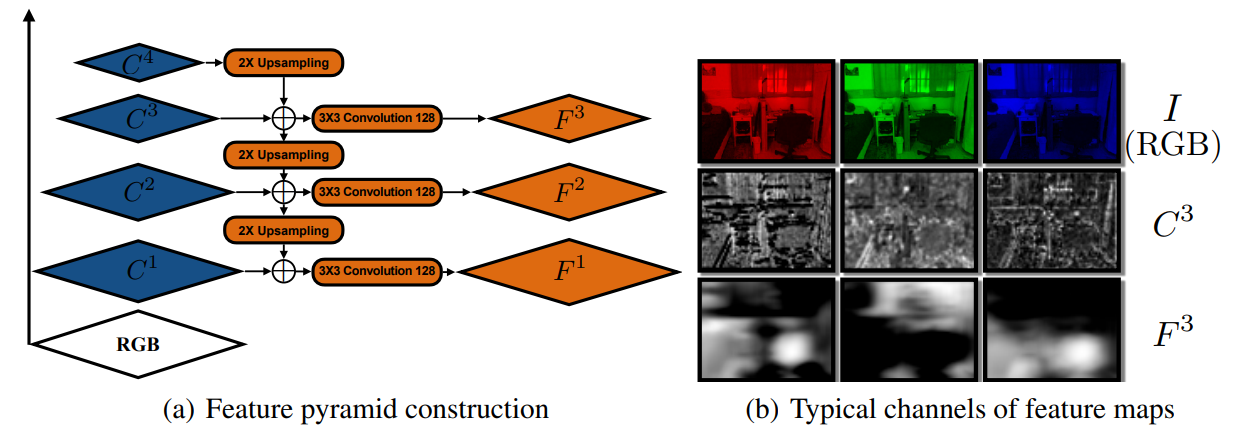
그림 2. 특징 추출을 위한 feature pyramid 구조 및 각 feature map의 시각화 결과

그림 3. 각 feature map 별 offset에 대한 변화량 시각화 결과

• 네트워크의 encoder 부분은 DRN-54(Yu et al., 2017)이라는 구조를 사용하였으며, 원래의 DRN-54는 dilation convolution을 사용했지만, BA-Net에서는 연산량을 줄이기 위해 보통의 3*3 convolution을 사용함

• 이렇게 구성된 encoder는 feature extraction 및 depth basis estimation을 위한 두 decoder에서 공유함

• Feature extraction은 feature pyramid networks(FPN)처럼 여러 크기의 feature를 추출하여 다양한 시야에 대응할 수 있도록 함

  • DRN-54의 conv1, conv2, conv3, conv4에서 마지막 residual block을 $\{ C^1, C^2, C^3, C^4 \}$라고 설정하며, 이는 각각 stride {1, 2, 4, 8}에 해당함

  • 각 $C^{k+1}$를 $C^k$의 크기와 일치하도록 bilinear interpolation을 통해 upsampling함

  • $C^k$와 upsampling된 $C^{k+1}$를 concatenate하여 $F^k$를 생성하고, 이렇게 $\{ F^1, F^2, F^3 \}$을 구성하여, 뒤에서 BA를 통한 최적화를 위한 feature로 사용(feature-metric bundle adjustment(BA)에서 사용되는 feature)

  • BA-Net에서는 pre-train된 backbone network의 feature를 사용하는 것이 아니라 위와 같이 정의된 $\{ F^1, F^2, F^3 \}$를 사용하여 BA 과정에 알맞는 feature가 출력되도록 네트워크를 학습시킴

  • 그 결과, <그림 2>의 (b)에서는 기존 DRN-54의 feature인 $C^k$와는 달리 $F^k$의 feature들이 각 영역 별로 구별되는 값을 갖고 있음

  • 또한, <그림 3>에서는 offset에 따른 각 feature 값의 차이를 볼 수 있는데, 다른 것들에 비해 $F^k$는 offset에 따라 확실히 구별되는 차이(offset이 적으면 적은 feature 값 차이, offset이 크면 큰 feature 값 차이)를 보이고, 이에 따른 확실한 global optima를 가지고 있어, 카메라의 pose를 최적화해야하는 BA 과정에 사용하기에 알맞는 feature라고 할 수 있음

• Depth basis는 "Deeper depth prediction with fully convolutional residual networks"라는 논문의 decoder 구조에서 마지막 단을 128 channel로 변형하여 사용

  • 일반적인 BA에서는 카메라 pose와 함께 3D point의 위치 또한 함께 최적화하며, 만약 모든 픽셀에 대한 depth 값을 최적화하고 $320 \times 240$ 크기의 이미지를 사용할 경우, 최적화 해야 할 파라미터의 수는 약 76.8k개가 되어 연산량이 크게 늘어남

  • BA-Net에서는 마지막 128 channel을 각각 basis로 활용하여 다음과 같이 최종 dapth map을 basis들의 선형 결합으로 추론함

  $\mathbb{D} = \text{ReLU}(\mathbf{w}^t \mathbf{B})$
  • 뒤의 BA 과정에서는 전체 depth 값이 아닌, 선형 결합의 128개 가중치인 $\mathbf{w}$만을 최적화하게 되어 효율적인 계산 가능

- Bundle Adjustment Layer

• 일반적인 BA 과정의 목적함수(photometric error)는 다음과 같고, $I_i$는 입력된 $i$th 이미지, $\mathbf{T}$는 transformation matrix, $\mathbf{q}_j$는 픽셀, $d_i \in \mathbb{D} = \{ d_j| j = 1, \cdots, N_j \}$는 $i$th 이미지의 각 픽셀 $\mathbf{q}_j$의 깊이정보를 의미하며, 최적화 대상이 되는 파라미터는 $\mathcal{X} = \{\mathbf{T}_1, \mathbf{T}_2, \cdots, \mathbf{T}_{N_i}, d_1, d_2, \cdots, d_{N_j} \}$이다.

  $e^p_{i,j}(\mathcal{X}) = I_i(\pi(\mathbf{T}_i , d_j \cdot \mathbf{q}_j ))-I_1(\mathbf{q}_j)$

  • ORB-SLAM 등에서 사용하는 re-projection error 기반 BA의 목적함수는 $e^g_{i,j}(\mathcal{X}) = \pi(\mathbf{T}_i , \mathbf{p}_j )-\mathbf{q}_{i,j}$이다(여기서 $\mathbf{p}$는 3D point).

  • 이러한 re-projection error 기반 BA는 이미지 상에 나타난 객체들의 꼭지점 및 가장자리 등의 정보만 활용한다는 점, 각 keypoint끼리의 matching이 필수적이지만 그 과정에서 outlier(서로 다른 keypoint끼리 matching되는 경우)들이 많아 RANSAC등의 추가적인 방법이 적용되어야 한다는 점, 하지만 이러한 방법들도 올바른 matching 결과를 보장하지 못한다는 점 등의 문제점을 가지고 있음

  • 위와 같은 이유로 저자들은 photometric error 기반 목적함수를 사용하고자 하였지만, 이 또한 error의 값이 non-convexity하게 증가하여 초기값에 매우 민감하다는 점, 이미지 색상에 영향을 주는 요소(광량 등)에 민감하다는 점, 움직이는 객체 등에 의해 발생하는 outlier에 민감하다는 점 등의 문제점을 가지고 있음

• 위와 같은 문제점을 해결하기 위해 저자들은 feature-metric difference에 기반한 BA 목적 함수를 제시함

  $e^f_{i,j}(\mathcal{X}) = F_i(\pi(\mathbf{T}_i , d_j \cdot \mathbf{q}_j ))-F_1(\mathbf{q}_j)$

  • 여기서 $\mathbb{F} = \{ F_i | i=1, \cdots, N_i \}$는 입력 이미지 $\mathbb{I} = \{ I_i | i=1, \cdots, N_i \}$의 feature를 의미하며, 위의 feature extraction 단계에서 추출된 값이다.

  • 즉, 여러 요소에 민감한 픽셀값 기반의 photometric error 대신, 신경망에 의해 추출되어 여러 요소에 강건하고, BA 과정에 최적화된 feature 값을 기반으로 목적함수를 구성하여 성능 향상을 이루고자 함

• 위에서 언급했듯이, 모든 픽셀에 대한 깊이 정보를 업데이트하면 업데이트 대상 파라미터가 너무 많아지는 문제가 발생하므로, basis depth 들의 가중치를 최적화하는 방식으로 최종적인 목적함수를 구성

  $e^f_{i,j}(\mathcal{X}) = F_i(\pi(\mathbf{T}_i , \text{ReLU}(\mathbf{w}^\top \mathbf{B}[j]) \cdot \mathbf{q}_j ))-F_1(\mathbf{q}_j)$

  • $\mathbf{B}$는 생성된 basis dapth들을 의미하며 $128 \times h \times w$크기이고, $\mathbf{B}[j]$는 $\mathbf{B}$의 $j$th column임

  • 즉, $\text{ReLU}(\mathbf{w}^\top \mathbf{B}[j]) \cdot \mathbf{q}_j$는 $\mathbf{q}_j$에 해당하는 depth가 됨

  • 초기값 $\mathbf{w}_0$를 학습하여 활용하면 더욱 빠른 수렴이 가능함

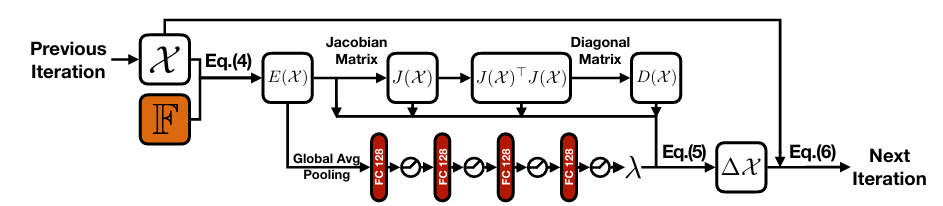
그림 4. BA layer의 single iteration 과정

• 이러한 목적함수를 사용하였을 경우, 이를 최적화 하기 위한 일반적인 Levenberg-Marquardt(LM) 알고리즘의 업데이트 식은 다음과 같음(참고)

  $\Delta \mathcal{X} = (J(\mathcal{X})^\top J(\mathcal{X}) + \lambda D(\mathcal{X}))^{-1}J(\mathcal{X})^\top E(\mathcal{X})$
  • 이때, $J(\mathcal{X})$는 Jacobian matrix, $J(\mathcal{X})^\top J(\mathcal{X})$는 근사된 Hessian matrix, $D(\mathcal{X})$는 $J(\mathcal{X})^\top J(\mathcal{X})$의 diagonal matrix, $\lambda$는 dumping factor이다.

• 따라서, <그림 4>와 같이 LM 알고리즘 과정을 구현하였으며, 그 과정에서 전체 과정을 미분 불가능하게 만드는 다음의 두가지 요소를 해결하여, 전체 파이프라인이 backpropagation을 통해 학습 될 수 있도록 함

  • 기존 LM 알고리즘은 일정 threshold 만큼 업데이트 과정이 수렴하여야 알고리즘 끝나는데, 이러한 if-else 기반의 종료 조건은 미분 불가능한 요소이므로 그냥 정해진 횟수(본 논문에서는 각 pyramid level에서 5번씩 총 15번)만큼 업데이트를 수행

  • Dumping factor $\lambda$ 또한 목적함수의 현재 값에 따라서 if-else 기반으로 결정되며(목적함수가 감소하지 않으면 $\lambda$를 크게하고, 목적함수가 감소하면 $\lambda$를 줄임), 본 논문에서는 이러한 문제를 해결하고 최적의 dumping factor를 찾아 성능을 향상시키기 위해 <그림 4>와 같이 MLP 구조를 통해 예측(현재의 목적함수 $E(\mathcal{X})$에 Global Average Pooling(GAP)를 적용하고 MLP에 입력)(ReLU를 사용하여 $\lambda$가 0보다 작아지지 안도록 함)

  • 최종적으로 LM 알고리즘 식에 따라 $\Delta \mathcal{X}$를 계산하고 다음 iteration에 입력하여 업데이트

- Loss Function

• Camera pose를 최적화하기 위한 loss, depth map을 최적화하기 위한 loss 두 가지로 구성됨

  • Camera Pose Loss: 단순한 L2 loss 사용
  $\mathcal{L}_{\text{rotation}} = |q-q^*|, \;\;\;\;\;\;\;\;\;\; \mathcal{L}_{\text{translation}} = |t-t^*|$
  • Depth Map Loss: BerHu Loss 사용
  $\mathcal{B}(x) = \begin{cases} |x| \;\;\;\;\;\;\;\;\;\; |x| \le c, \\ \frac{x^2 + c^2}{2c} \;\;\;\;\;\;\; |x| \gt c \end{cases}$

3. 실험 결과(Experiments)

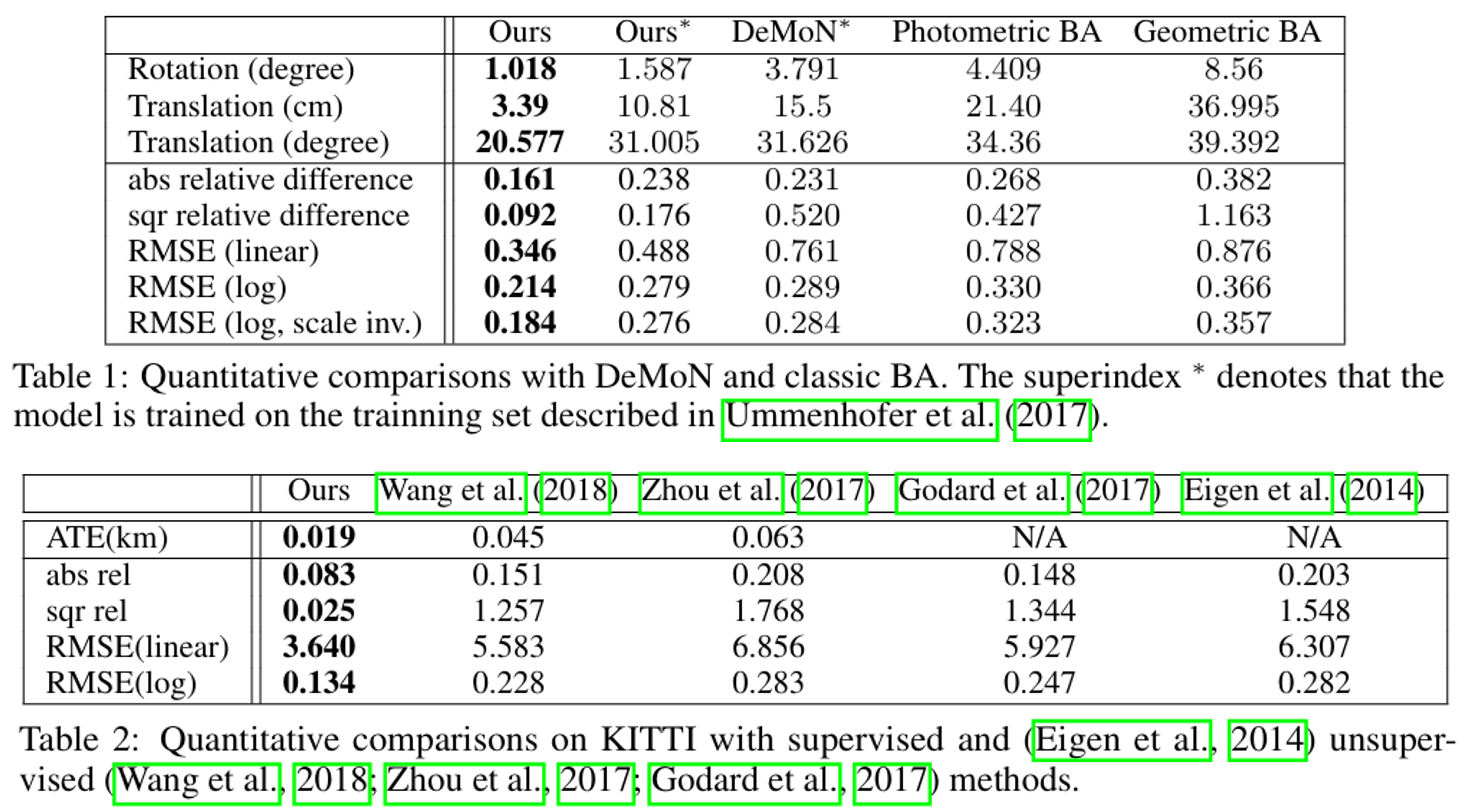
그림 5. DeMoN, KITTI 데이터셋 적용 결과

• DeMoN, KITTI 등의 데이터셋에서 높은 성능을 달성

• 전체 모델의 동작 시간은 약 95.21ms(backbone(DRN-54): 15.04ms, Feature Pyramid: 5.87ms, Basis Depth Generator: 9.81ms, BA-Layer Optimization: 67.22ms)

  • 하드웨어 정보는 따로 밝히지 않았지만, GPU 메모리가 12gb라고 함

  • BA-Layer Optimization 과정이 가장 많은 연산 시간을 요구

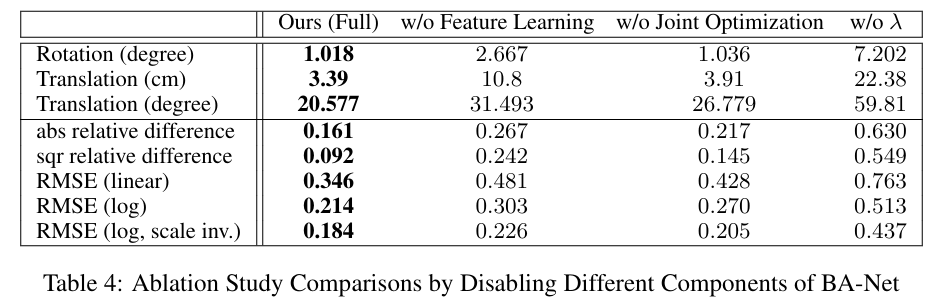
그림 6. Ablation Study 결과

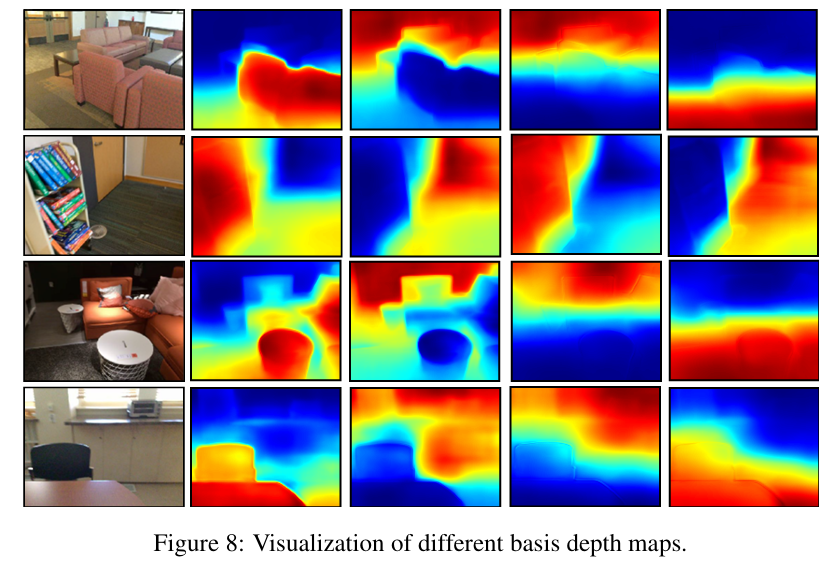
그림 7. Basis depth map 예시

개인적인 생각

• 저자들이 제시한 미분 불가능 요소들이 실제로 문제가 되는 지는 의문
• If-else 들이 미분 불가능 요소가 맞긴 한데, tensorflow나 pytorch같은 딥러닝 프레임워크를 써서 전체 코드를 작성하면 그냥 backpropagation 될 거 같다는 생각??(일단, loss function으로 사용하는 BerHu Loss 부터가 조건문이 들어가 있기도 하고...)