학습 주제
힙(Heaps)

학습 내용

힙 (heap) 도 이진 트리의 한 종류입니다. 이진 힙 (binary heap) 이라고도 부릅니다. 힙은 데이터 원소들의 순서를 교묘하게 표현한 트리입니다. 따라서 데이터의 정렬에도 이용할 수 있는데, 힙을 이용하여 데이터를 정렬하는 알고리즘을 힙 정렬 (heap sort) 이라고 부릅니다.
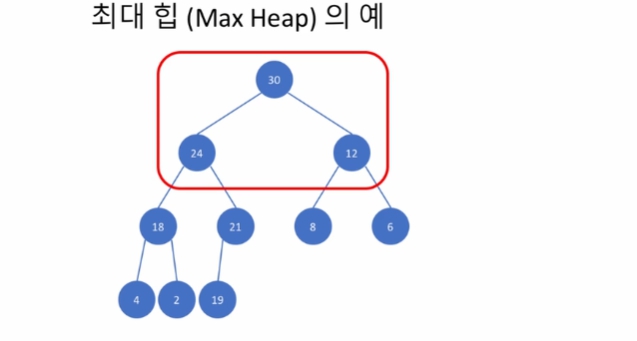
힙에는 최대 힙 (max heap) 과 최소 힙 (min heap) 이 있습니다. 최대 힙과 최소 힙은 데이터 원소의 순서 기준이 내림차순이냐 오름차순이냐만 달라지고 완전히 대칭이므로, 여기에서는 최대 힙을 기준으로 설명을 전개하겠습니다. 최대 힙은 세 가지의 성질을 유지하고 있는 이진 트리입니다. 그 세 가지 성질은:
루트 노드가 항상 최댓값을 가진다.
완전 이진 트리이다.
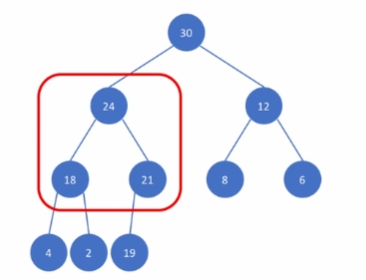
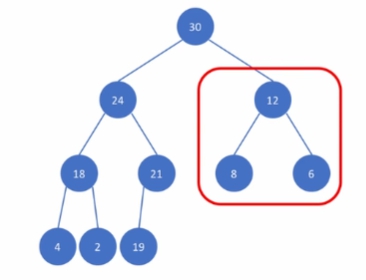
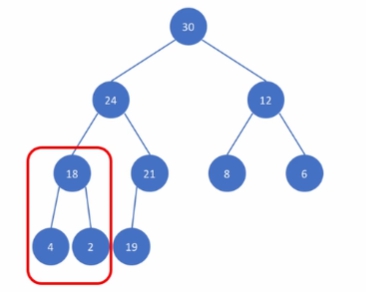
최대 힙 내의 임의의 노드를 루트로 하는 서브트리 또한 최대 힙이다.
입니다. 마지막 성질은 트리에서 매우 자주 맞닥뜨리게 되는 재귀적인 정의네요.
앞에서 (제 20 강과 제 21 강에서) 살펴본 이진 탐색 트리 (binary search tree) 와 최대 힙은 조금 다른 특징을 가집니다. 이진 탐색 트리에서는 원소들이 완전히 크기 순서대로 정렬되어 있습니다. (따라서 중위 순회를 하면 데이터를 정렬된 순서로 뽑아낼 수 있습니다.) 최대 힙은 완전히 크기 순서대로 정렬되어 있지는 않습니다. (따라서 트리를 순회함으로써 데이터를 정렬할 수는 없습니다.) 또한, 이진 탐색 트리에서는 루트 노드로부터 시작하여 특정 원소를 빠르게 검색할 수 있는 반면, 최대 힙은 이러한 탐색 연산을 제공할 수 없습니다.
그렇다면 최대 힙의 장점은 무엇일까요? 바로 부가의 제약 조건, 즉 완전 이진 트리 (complete binary tree) 여야 한다는 제약 때문에, n 개의 노드로 이루어진 최대 힙의 높이 (깊이) 는 log(n) + 1 (에서 소수 부분은 버림) 로 정해집니다. 이 성질 때문에 데이터 원소의 삽입/삭제 연산의 실행 시간은 언제나 log(n) 에 비례합니다. 따라서, 어떤 최대 힙이 존재할 때, 이 힙으로부터 반복적으로 루트 노드를 삭제하면 (서 데이터 원소들을 꺼내면) 루트 노드에 들어 있는 키가 힙 내에서 최대임이 보장되어 있으므로 데이터를 내림차순으로 정렬할 수 있고, 이 정렬에 소요되는 시간 또한 log(n) 에 비례합니다.
힙이 항상 완전 이진 트리라는 성질은 트리의 표현에 있어서도 이점을 제공합니다. (동영상 강의에서 소개될) 규칙에 따라 노드들에 번호를 매기면, 이 번호 순서로 이루어진 선형 배열에 트리를 표현할 수 있습니다. 또한, 완전 이진 트리이므로 노드의 추가와 삭제는 배열의 맨 마지막 원소에서만 일어납니다.
최대 힙을 추상적 자료 구조로 정의하고, 원소의 삽입 연산인 insert() 를 설명하겠습니다. 원소의 삽입은 맨 마지막 노드에서 일어나므로, 우선 맨 마지막 노드에 주어진 데이터를 임시로 붙인 뒤에 이 원소를 부모 노드의 키와 비교하여 더 큰 경우에는 그 부모와 위치를 맞바꿉니다. 이 과정을 루트 노드에 도달할 때까지 또는 더이상 맞바꿀 필요가 없을 때까지 반복하면 삽입이 완료됩니다. 그냥 말로 설명하면 얼핏 이해가 어렵게 느껴질 수 있습니다만, 동영상 강의에 포함된 예제 그림을 통해서 이해해보세요.
이제는 연습이 잘 되어 있어서 이런 정도의 코드는 어렵지 않게 작성할 수 있을 것으로 기대합니다. 연습 문제로 insert() 메서드를 작성해보세요.

포화 이진트리랑 구분해야함.

모든 노드는 자신 자식보다 크다

재귀적으로도 정의됨
어느 노드를 루트로 하는 스브트리도 모두 최대 힙

왼쪽, 오른쪽 subtree는 정의되지 않음. 상대적인 순서는 정의되어 있지 않음
느슨한 정렬이라고도 봄

Heap은?
1. 이진 탐색 트리에선 그렇다. 힙은 X 느슨하게 되어 있음
2. 이진 탐색 트리는 빠르게 검색할 수 있는 구조 제공. 힙은 검색하는데 좋은 방법이 없음
3. 이진 탐색 트리 보단, 완전 이진 트리라는 제약 조건 있음

-insert 아이템 삽입

• remove 최대/최소 원소는 (root node) 동시에 이 노드를 삭제
  traverse, search는 제공되지 않음. 관심사항이 아님

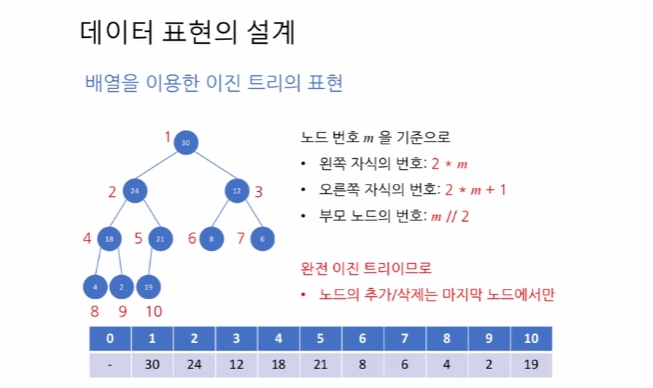
번호 계산법.
완전 이진 트리이므로, 추가 삭제는 끝에서만 이뤄짐
값을 삽입 할 때 중간값의 경후 치환이 필요할 텐데, 그때의 연산도 필요해 보인다

0은 사용하지 않음. 보다 계산하기 편리하게 하기 위해.

완전 이진 트리 이기 때문에 배열로 사용이 가능하고, 적당한 방법임.

0번 인덱스는 버리므로 None으로 초기화

부모 노드가, 양쪽 자식 보다 커야하는 조건을 만족시켜야 하기 때문에 마지막 노드에서 부모 노드와 비교하면서 위로, 위로 올라가는 방식. 자식 간 우열은 고려하지 않음.

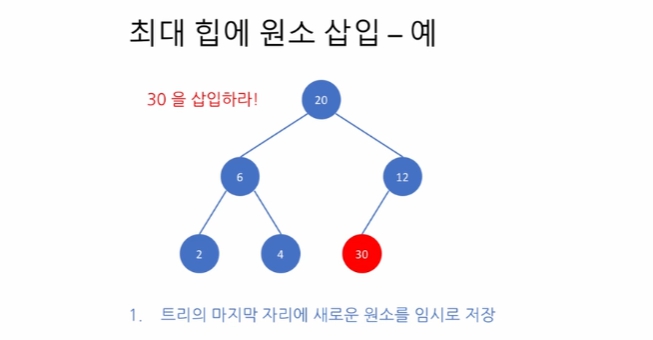
재귀적으로 부모 노드의 key와 비교한 뒤, 교체하고, 또 다시 자신의 부모노드와 비교하여 올라감

높이가 logn으로 제한됨

삽입 연산의 구현

튜플로 사용하면 두 변수의 값을 바꾸면 보다 편리함.

연습문제

내 풀이

class MaxHeap:

    def __init__(self):
        self.data = [None]


    def insert(self, item):
        # 0번 인덱스는 사용하지 않음. 계산의 편리함을 위해
        # 부모 노드 인덱스를 구하는 법 node.key // 2
        # 부모 노드에서 왼쪽 인덱스 parent.key * 2
        # 부모 노드에서 오른쪽 인덱스 parent.key * 2 + 1
        # 아이템을 마지막 인덱스에 저장
        self.data.append(item)
        
        # 본인의 인덱스, 부모의 인덱스 저장
        curr_key = self.data.index(item)
        parent_key = curr_key // 2
        
        # 부모의 value와, 본인의 value 비교
        # 본인의 value가 부모의 value보다 더 클 경우 계속 위로 이동,
        if parent_key == 0:
            pass
        else:
            while self.data[curr_key] > self.data[parent_key]:
                self.data[curr_key], self.data[parent_key] = self.data[parent_key], self.data[curr_key]
                curr_key = parent_key
                parent_key = curr_key // 2

                if parent_key == 0:
                    break


def solution(x):
    return 0

어려웠던 점
처음 루트 노드에 값을 넣을 때를 상정하지 않아서 while 문에서 0 번째 인덱스에 접근하려 해서 오류가 났다. 애초에 값이 None이기 때문에 비교연산자 사용이 불가.
뭔가 오류가 나면 땜빵 메우는 식인 느낌이라, 리팩토링하는 연습을 더 길러야겠다.