학습 주제
이진 탐색트리 기능 중 삭제

학습 내용
이진 탐색 트리 삭제 기능 구현

지난 강의 (제 20 강) 에서 이진 탐색 트리 (binary search tree) 를 소개하고 아래와 같은 연산을 정의했습니다. (기억나나요?)
insert(): 트리에 주어진 데이터 원소를 추가
remove(): 특정 원소를 트리로부터 삭제
lookup(): 특정 원소를 검색 (탐색)
inorder(): 키의 순서대로 데이터 원소들을 나열
min(), max(): 최소 키, 최대 키를 가지는 원소를 각각 탐색
이 중 remove() 를 제외한 연산들은 꽤 간단했습니다. 지난 강의에서 코드를 함께 검토하기도 했고, 연습문제로 풀어보기도 했습니다.
그런데, remove() 연산은 나머지 다른 연산들보다 조금 복잡합니다. 트리에서 리프 노드가 삭제되는 경우에는 별로 할 일이 많지 않지만, 루트 노드 또는 내부 노드가 삭제되는 경우에는 다른 노드들을 이리저리 옮겨서 트리의 모습을 갖추도록 구조를 조정해야 하기 때문입니다. 이 때, 삭제 연산이 끝난 이후의 트리도 (당연히) 이진 탐색 트리의 성질을 만족해야만 합니다. 다시 말하며, 이 연산을 구현할 때 트리를 조정함에 있어서 이진 탐색 트리의 모습을 유지하도록 알고리즘을 구성해야 한다는 뜻입니다.
자세한 알고리즘은 동영상 강의를 참고하세요. 이런 경우와 저런 경우 등을 나누어 생각해야 하기 때문에 알고리즘의 설계도 지금까지의 것들보다 조금 복잡하고, 코드의 구현도 이제는 조금 어려워진 느낌입니다. 하지만, 이 정도의 코드를 능숙하게 작성할 수 있다면, 이 강의에서 다루는 내용보다 더 발전된 알고리즘들 (제 17 강에서 언급한 바와 같이, 여러 종류의 트리와 이에 기반한 알고리즘들이 있어서 더욱 고급의 기능을 제공합니다) 을 설계, 구현할 수 있는 바탕이 마련되었을 것입니다. 연습문제로 코드를 직접 작성해 보세요. 지금쯤은 처음에 비해서 상당히 코딩 기술이 늘어 있음을 발견하게 되지 않나요?
이전 강의 (제 21 강) 에서, 이진 탐색 트리가 효과를 발휘할 수 없는 특수한 경우가 있다고 했습니다. 어떤 경우가 해당할까요? 만약 트리가 한 줄로 늘어서면 (즉, 모든 노드가 왼쪽 또는 오른쪽의 한 자식만을 가지는 경우) 노드의 개수가 n 이라 할 때 트리의 높이 (깊이) 또한 n 입니다. 이 경우 특정 원소를 탐색하면 이 탐색 연산의 복잡도는 선형 탐색 (linear search) 와 동일해집니다. 즉, 이진 탐색 트리를 애써 만들어 둔 것이 무색해지는 것이죠.
이 한계점은, 이진 탐색 트리에 원소를 삽입함에 있어서 높이를 최소화하려는, 즉 트리의 좌우 균형을 유지하려는 노력을 하지 않았기 때문입니다. 이런 한계를 극복하기 위해서 이진 탐색 트리에 추가의 제약을 (만족해야 하는 성질을) 부가한 트리들이 있습니다. 이 강의에서는 다루지 않지만, 이후 발전 학습을 원하는 경우 아래 트리들을 공부해 보세요.
AVL trees
Red-black trees

어쩌다 보니 수업을 듣지 않고 바로 실습 부터 풀어버렸다. 어쩐지 배운적이 없는 것 같은데, 평소보다 실습 난이도가 높아진 느낌이었다. 오후 내내 고생해서 그래도 풀었더니 보람이 있다.

여기서 특이하게 찾은 노드의 부모노드도 알고 있어야 한다고 했는데, 이는 삭제 후에 부모 노드와 그 자식 노드를 이어 주어야 하기 때문이다.

인터페이스의 설계

세부적인 걸 바로 짜기엔 복잡하다. 따라서 큰 그림부터 그려나가야 한다.
lookup(key)로 삭제하려는 키값을 가진 노드가 트리 내에 있느지 확인을 하고, 없다면 False
있으면 삭제를 수행한다

삭제되는 노드가

• 자식이 0 (말단 노드, 제일 맨 아래에 있음)
• 자식이 1
• 자식이 2
  

-> 부모 노드의 삭제된 노드 부분을 None

subtree가 삭제되는 자리로 올라오게 됨.

부모 노드의 링크를 subtree에 연결함

이번 수업에서는 바로 다음 큰 키를 사용 (바로 전 작은 키를 사용해도 됨)

자식을 세어보는 메서드를 별도로 생성함. (삭제 처리의 분기점 제공)

말단 노드를 삭제, 이 때 parent 노드의 링크를 None으로 해주어야 하기 때문에 parent를 알아야함

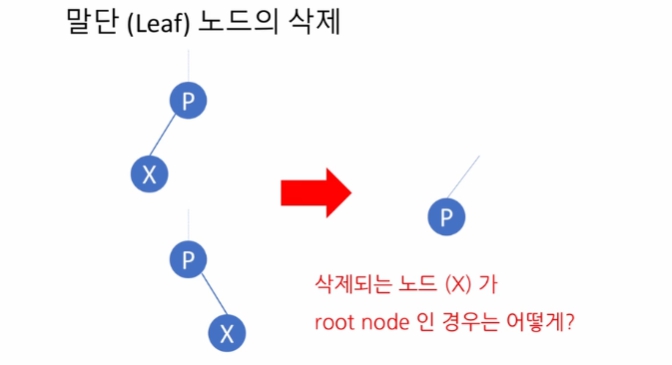
단, 삭제하는 노드가 유일한 노드, 부모가 없는 노드일 경우, 트리 자체를 삭제함.
딱 본인의 부모, 자식 수준만 생각하면됨, 다른 형제 조상은 신경쓰지 않아도 됨

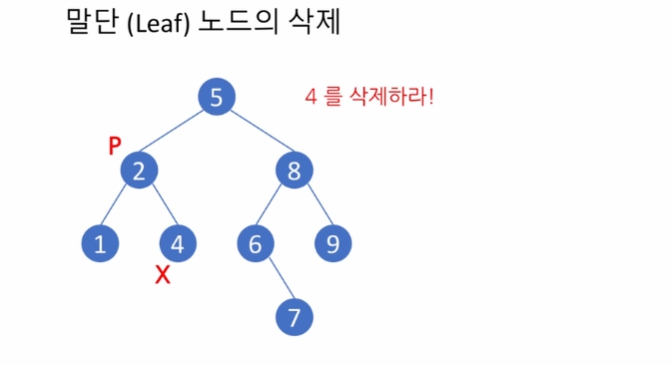
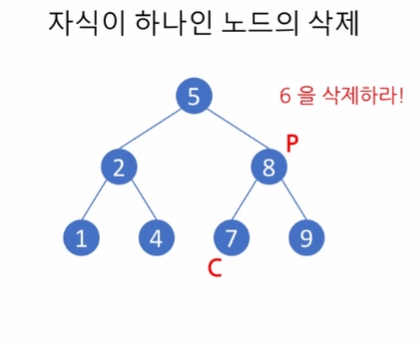
2의 오른쪽 링크를 None으로 하면 삭제 됨.

삭제 해도, 이진 탐색 트리의 모양이 변하진 않음.

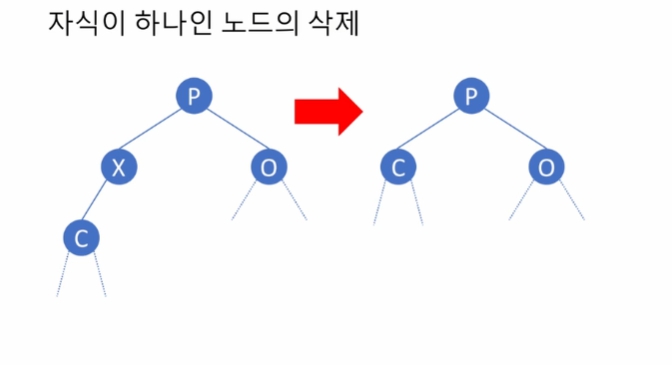
값을 대신 집어넣고, 부모 노드 -> 노드의 자식과 링크 조절

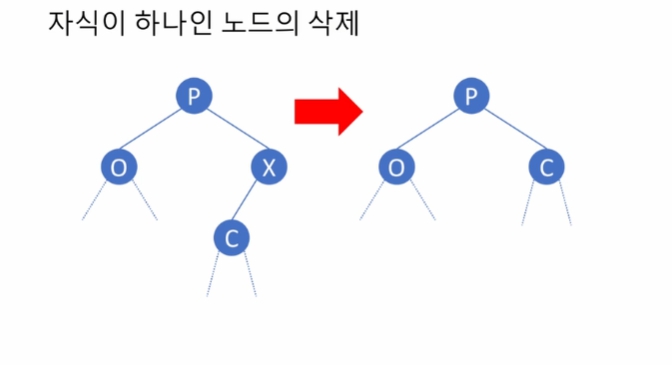
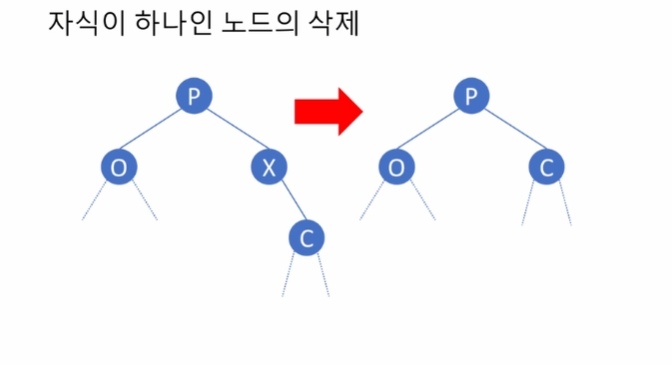
parent 노드의 링크를 잘 조절해 주어야 함.

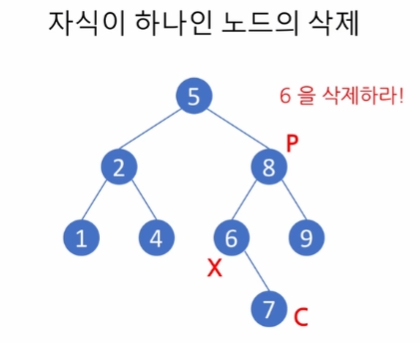
P.left = Node.right 링크 연결

자식이 둘인 노드의 삭제

강조한 이유는 조금 더 생각할 것이 있다

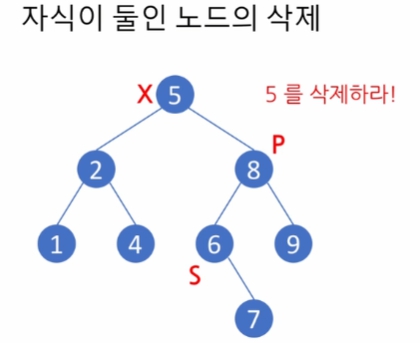
오른쪽 자식 노드에서 왼쪽으로 따라가면 대체에 적합한 노드가 있고, 이를 successor 라 한다

successor 를 6 위치에 대입한다

successor의 왼쪽 차일드는 존재할 수 없음. 제일 왼쪽까지 내려간 값.
대신 오른쪽 차일드는 있을 수 있기에 부모 8과 연결 해줘야 함.

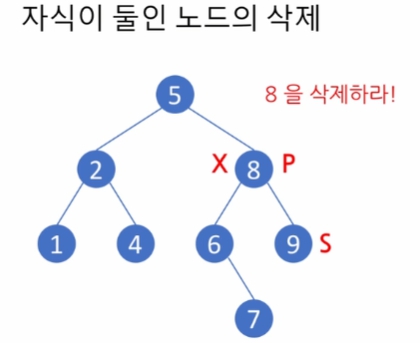
parent -> successor로 대체하고, parent 오른쪽 링크를 None으로 조절한다.
if 조건문으로 별도의 이 조건을 다루어줘야 함.

이진 탐색 트리가 별로 효율적이지 못한 경우

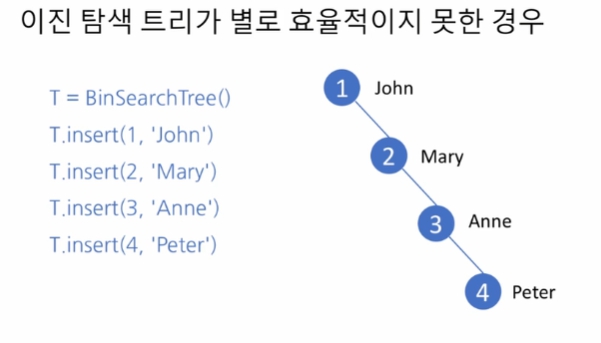
인접한 데이터가 입력될 경우, 한쪽으로 치우쳐 균형이 잡혀있지 않다.
4를 찾게 될 경우, 1, 2, 3 순으로 탐색하다보니 선형 탐색 수준의 복잡도를 갖게됨.
Tree의 왼쪽 오른쪽이 균형있게 나누어 져 있어야 함.

큰키 -> 작은키도 마찬가지임

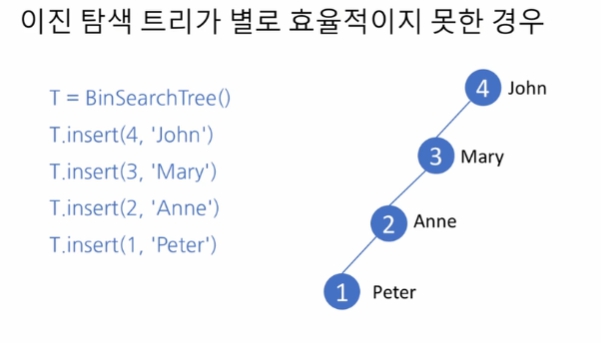
왼쪽으로 치우진 이진 탐색 트리인 모습을 볼 수 있다.

트리가 제 구실을 하려면 높이가 일정하고 균형을 잡아야 함
보다 나은 이진 탐색 트리 등이 있다.

AVL tree

Red-black tree

O(logn) 보장함

문제 풀이

내 풀이

이전 20강 하단에 풀이됨.

어려웠던 점.
지난번에 자식노드가 2개인 경우, successor의 자식이 있을 경우를 상정하라고 했는데, 역시 left는 존재하지 않고, right가 있을 경우, 없을 경우에 대해 대처하면 되었다.
하지만 나는 left도 있다고 가정하고 짜서 과하게 짰다.
일단 테스트는 성공했다.