학습 주제
이진 탐색 트리
학습 내용
이진 탐색 트리의 구현
이진 탐색 트리 (binary search tree) 는 이진 트리의 일종입니다. 그런데 이름이 낯설지를 않네요? 제 3 강에서 이진 탐색 (binary search) 알고리즘을 가볍게 다룬 적이 있습니다. 이진 탐색 알고리즘과 이진 탐색 트리를 이용한 탐색 알고리즘은 똑같은 것은 아닙니다. 하지만 많이 닮아 있습니다.
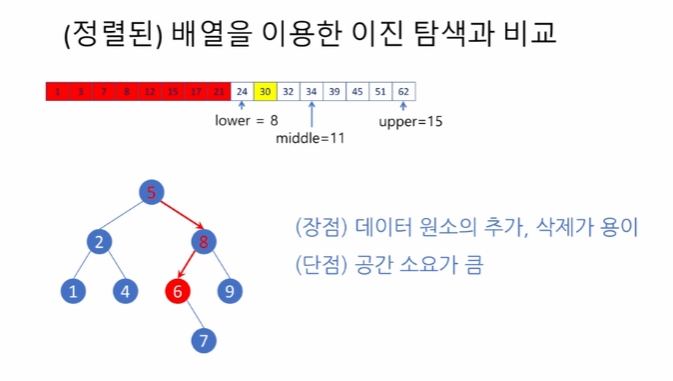
이진 탐색 알고리즘이 기억나나요? 이미 정렬된 선형 배열을 대상으로, 배열을 절반씩 잘라 가면서 찾고자 하는 원소 (또는 키 - key) 가 들어 있을 수 없음이 보장되는 절반을 탐색 대상에서 제외함으로써 매 반복에서 탐색 대상이 되는 배열의 길이를 반으로 만들어 나가는 알고리즘입니다. 따라서 이 알고리즘의 실행 시간은 배열의 길이를 n 이라고 할 때 log(n) (밑은 2 입니다) 에 비례합니다. 이진 탐색을 적용하기 위해서는 탐색 대상인 배열이 미리 정렬되어 있어야 하므로, 이 배열에 데이터 원소를 추가하거나 배열로부터 데이터 원소를 삭제하는 일은 n 에 비례하는 시간을 소요합니다.
이진 탐색 트리에서는, 모든 노드에 대해서 왼쪽 서브트리에 들어 있는 데이터는 모두 현재 노드의 값 (키) 보다 작고 오른쪽 서브트리에 들어 있는 데이터는 모두 현재 노드의 값 (키) 보다 크도록 트리를 유지합니다. 다시 말하면, 이러한 성질을 만족하는 이진 트리를 이진 탐색 트리라고 부릅니다.
탐색을 할 때는 루트 노드에서 시작해서 한 번에 한 단계씩 간선을 따라 아래로 아래로 내려갑니다. 어느 노드를 방문했을 때, 이 노드에 담긴 데이터 원소보다 찾고자 하는 키가 더 작은 경우에는 왼쪽 서브트리를, 더 큰 경우에는 오른쪽 서브트리를 택합니다. 반대쪽 서브트리에는 찾고자 하는 값이 없음을 보장할 수 있으니까 탐색할 필요가 없다는 성질을 이용하는 것이죠. 이렇게 해서 리프 노드에까지 이르렀는데도 그 사이에 찾고자 하는 값을 만나지 못하면 이 이진 탐색 트리에는 찾으려는 값이 없다는 것을 알 수 있습니다. 이 알고리즘에서도 뭔가 재귀적인 냄새가 나지 않나요? 당연합니다. 트리라는 자료 구조가 매우 재귀적인 성질을 가지고 있으니까요.
이 강의에서는 이진 탐색 트리를 추상적 자료 구조로 정의하는데, 아래와 같은 연산을 제공하도록 합니다.
- insert(): 트리에 주어진 데이터 원소를 추가
- remove(): 특정 원소를 트리로부터 삭제
- lookup(): 특정 원소를 검색 (탐색)
- inorder(): 키의 순서대로 데이터 원소들을 나열
- min(), max(): 최소 키, 최대 키를 가지는 원소를 각각 탐색
이 중 가장 중심이 되는 연산은 탐색 (lookup) 입니다. 이 연산의 실행 시간은 트리의 높이 (또는 깊이) 에 비례하므로, 평균적으로 (노드의 개수, 즉 데이터 원소의 개수를 n 이라 할 때) log(n) 에 비례합니다. 또한, 선형 배열이 아닌 트리 구조를 택하기 때문에 삽입/삭제 (insert/remove) 연산 또한 평균적으로 log(n) 에 비례하는 시간을 소요합니다. 왜 "평균적" 이라고 했냐면, 어떤 특수한 경우에 대해서는 이진 탐색 트리가 효과를 발휘할 수 없는 모습을 가지기 때문인데, 그 얘기는 다음 강의 (제 21 강) 에서 하겠습니다.
이번 강의에서는, 재귀적인 방법으로 위 연산들 중 inorder(), min(), max(), 그리고 lookup() 을 함께 구현해봅니다. 연습문제로는 insert() 를 구현하는 코딩을 실습합니다.
트리의 경우 생성할 때 미리 정렬되어 있는 점을 이용해서 이진 탐색이 가능하게 한다.
중복된 데이터는 없는 것으로 가정하고 검색을 한다. 값이 같은경우.
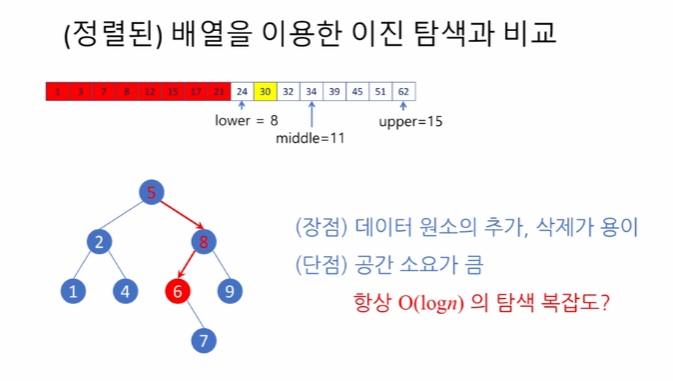
이진 탐색 트리가 항상 lon(n)을 가지진 않음. 그래서 평균적이라 명시
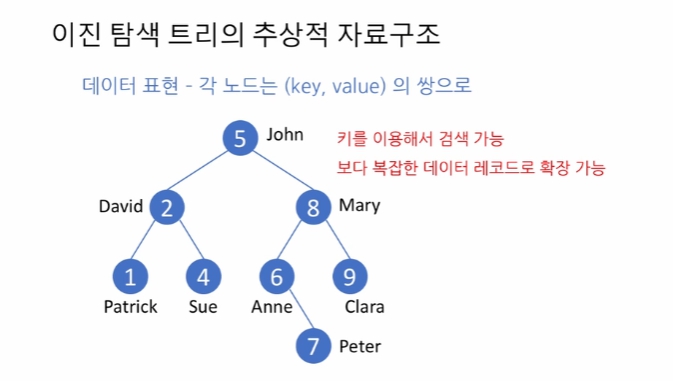
각 노드를 (key, value)로 구현하였다. 이후 value에 어떤 값이 들어가냐에 따라 보다 복잡한 레코드로 확장이 가능하다. 저장과 탐색은 key에 따라 이뤄진다

삭제 - subtree가 끊어지지 않게 다시 연결해줘야 하기 때문이라 생각
같은 값이 없기 때문에, 트리 구조 변경이 없고, 아래로 줄줄이 달리는 형태
코드 구현


in-order 는 거의 똑같음. 노드를 반환하는 점에서 다름


min() 메서드 구현
모든건 root 노드가 존재해야함. 아니면 접근을 할 수 가 없음

결국 제일 왼쪽 값이 작기 때문 중위 순회 방식
max()의 경우 반대로 제일 오른쪽 값 아니면 자기 자신이 최대값

부모 노드도 함께 리턴해야함. 원소 삭제에서 알 필요가 있기 때문. 각각, 없으면 None으로
루트 노드일 경우, 부모는 None

순서쌍 none, none (튜플)

자신 노드의 key와 비교 후 작을 때 재귀적으로 호출하는 모습이다. 기본 (default) 매개변수는 없을 시, 부모가 없다고 가정함. (최초, 루트 노드부터 시작하기 때문 이후엔 자기 자신을 부모노드로 넘김)
없을 시, None, None 리턴

찾았을 경우,

코드 구현 - insert()

root가 존재여부로 분기점 생성

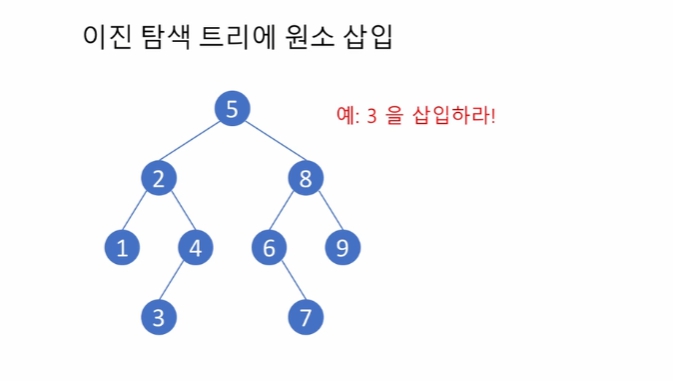
연습 문제 - 원소 삽입 연산 구현
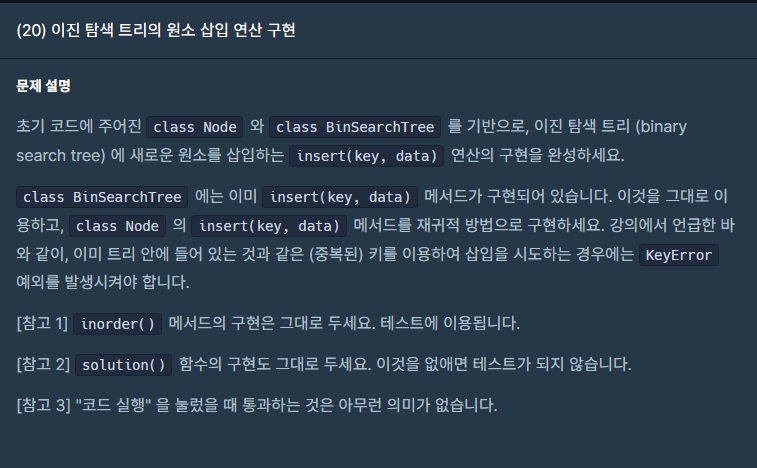
내 풀이
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
def insert(self, key, data):
if key < self.key:
if self.left:
self.left.insert(key,data)
else: self.left = Node(key, data)
elif key > self.key:
if self.right:
self.right.insert(key, data)
else: self.right = Node(key, data)
else:
raise KeyError('')
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
class BinSearchTree:
def __init__(self):
self.root = None
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else:
self.root = Node(key, data)
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def solution(x):
return 0어려웠던 점.
현재 키와 같은 경우는 어떻게 해야될까? 잘 모르겠다. 현재 문제에선 key가 같은 경우를 제외하였음.
연습 문제 - 노드의 삭제 연산 구현
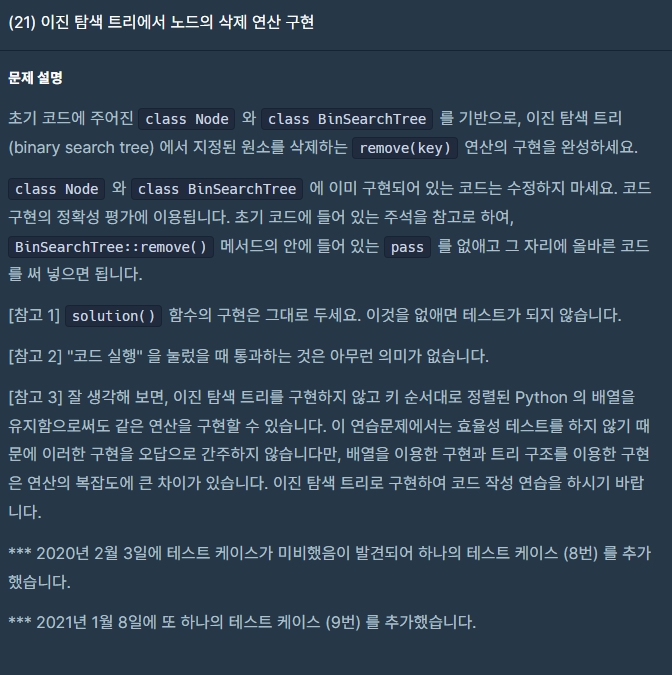
아이디어
-
삭제할 노드가 존재 하는 상황 (없으면 False 반환)
-
현재 삭제할 노드의 자식 노드의 갯수에 따라 다른 연산을 함
- 자식 노드의 갯수가 0개일 경우
- 부모의 노드가 존재할 경우: node가 왼쪽, 오른쪽 자식인지 확인하여 자식을 끊어냄.
- 부모의 노드가 존재하지 않을경우: node가 root일 경우이므로, self.root -> None
- 부모의 노드가 존재할 경우: node가 왼쪽, 오른쪽 자식인지 확인하여 자식을 끊어냄.
- 자식 노드의 갯수가 1개일 경우
- 하나 있는 자식이 왼쪽인지 오른쪽인지 판단하여, 그 자식을 어떤 변수가 가리키도록 한다.
- 부모 노드가 존재할 경우: node가 왼쪽, 오른쪽 자식인지 확인하여, 위에서 가리킨 자식을 대신 node의 자리에 채워넣음
- 부모 노드가 존재하지 않을경우: node가 root인 경우이므로, self.root -> node의 자식
- 하나 있는 자식이 왼쪽인지 오른쪽인지 판단하여, 그 자식을 어떤 변수가 가리키도록 한다.
- 자식 노드의 갯수가 2개로 양쪽 다 존재하는 경우
- 두가지 방법이 있음. 기존 삭제할 노드를 대체할 successor를 어떻게 얻느냐에 따라.
- left child 중 가장 큰 node
- right child 중 가장 작은 node
- 노드를 대체할 그 subtree에서 다음 중앙값으로 적합.
- 이번엔 2. 방법으로 시도함.
-
parent -> node (삭제할 노드)
-
successor -> node.right (오른쪽 자식노드)
-
while 문으로 오른쪽 자식 중 가장 왼쪽 노드 반환
-
이때 parent는 그 노드의 부모 노드를 가리키도록 찾아냄. lookup() 사용
-
삭제하려는 노드인 node에 successor 의 key 와 data 를 대입
-
successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지 판단하여,
-
그에 따라 parent.left 또는 parent.right 를
-
successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 한다.
-
-
- 자식 노드의 갯수가 0개일 경우
내 풀이
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
def insert(self, key, data):
if key < self.key:
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key, data)
elif key > self.key:
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else:
raise KeyError('Key %s already exists.' % key)
def lookup(self, key, parent=None):
if key < self.key:
if self.left:
return self.left.lookup(key, self)
else:
return None, None
elif key > self.key:
if self.right:
return self.right.lookup(key, self)
else:
return None, None
else:
return self, parent
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
def countChildren(self):
count = 0
if self.left:
count += 1
if self.right:
count += 1
return count
class BinSearchTree:
def __init__(self):
self.root = None
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else:
self.root = Node(key, data)
def lookup(self, key):
if self.root:
return self.root.lookup(key)
else:
return None, None
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
# The simplest case of no children
if nChildren == 0:
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# parent.left 또는 parent.right 를 None 으로 하여
# leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
if parent:
# node가 왼쪽 자식일 경우,
if parent.left == node:
parent.left = None
else:
parent.right = None
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 를 None 으로 하여 빈 트리로 만듭니다.
else:
self.root = None
# When the node has only one child
elif nChildren == 1:
# 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
# 그 자식을 어떤 변수가 가리키도록 합니다.
if node.left:
delete_child = node.left
else:
delete_child = node.right
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
if parent:
if parent.left == node:
parent.left = delete_child
else:
parent.right = delete_child
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 에 위에서 가리킨 자식을 대신 넣습니다.
else:
self.root = delete_child
# When the node has both left and right children
else:
parent = node
successor = node.right
# parent 는 node 를 가리키고 있고,
# successor 는 node 의 오른쪽 자식을 가리키고 있으므로
# successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
# 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
# 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
while successor.left:
# 키보다 다음으로 큰 키를 반환함.
successor, parent = successor.left, successor
# 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
node.key = successor.key
node.data = successor.data
# 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
# 그에 따라 parent.left 또는 parent.right 를
# successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
# successor 가 부모 노드의 어느쪽 자식인지,
# successor의 어느쪽 자식이 남아 있는지 (양쪽다 있다고 가정은 X)
if parent.key > successor.key:
if successor.left:
parent.left = successor.left
elif successor.right:
parent.left = successor.right
else:
parent.left = None
else:
if successor.left:
parent.right = successor.left
elif successor.right:
parent.right = successor.right
else:
parent.right = None
return True
else:
return False
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def solution(x):
return 0어려웠던 점
삭제할 노드의 자식 노드가 2개 있는 상황에서,
Successor는 삭제 노드의 오른쪽 자식 중 가장 작은 값으로 정한 조건을 맞추기 위해
while 문을 어떻게 사용해야 하는지 그게 헷갈렸다.
while successor.left:
# 키보다 다음으로 큰 키를 반환함.
successor, parent = successor.left, successor
# 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
node.key = successor.key
node.data = successor.data
# 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
# 그에 따라 parent.left 또는 parent.right 를
# successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
# successor 가 부모 노드의 어느쪽 자식인지,
# successor의 어느쪽 자식이 남아 있는지 (양쪽다 있다고 가정은 X)
if parent.key > successor.key:
if successor.left:
parent.left = successor.left
elif successor.right:
parent.left = successor.right
else:
parent.left = None
else:
if successor.left:
parent.right = successor.left
elif successor.right:
parent.right = successor.right
else:
parent.right = None
while 문 내에서
나는 어떻게는 lookup을 사용해야되는 줄 알고 계속 쓰려고 했었지만, lookup는 말 그대로 원하는 key 값을 '정확히' 찾아주는 메서드이고, 나의 경우는 삭제할 노드의 key 값과 최대한 '근사한' 값을 구해야 하는 상황이라 절대 나올 수 가 없었다. 그걸 구현할 메서드는 따로 없고, 이진 트리에 특성상, 오른쪽 자식노드에서 가장 왼쪽 후손이 본인과 제일 근사한 key 값을 가진다는 성질을 이용하여, while 문에서 왼쪽을 계속 탐색하도록 했고, 맞출 수 있었다.
다만
# 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
# 그에 따라 parent.left 또는 parent.right 를
# successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
# successor 가 부모 노드의 어느쪽 자식인지,
# successor의 어느쪽 자식이 남아 있는지 (양쪽다 있다고 가정은 X)왼쪽 노드까지 순회한 후, 그 successor의 자식이 있을 껄 가정한건 이해가 잘 되지 않았다. 왼쪽으로 계속 순회하게 되면 자료가 없게되지 않나? 또 자식이 두명일 경우 이를 부모에 연결하면 3개를 갖게되나? 이런 물음 속에서 이진 탐색 트리에선 사용하지 않겠지만, 다른 트리에서는 사용 할 수 있다는 가능성을 남겨두고 마친다.
