학습 주제
넓이 우선 순회
학습 내용
넓이 우선 순회 구현
지난 깊이 우선 순회는 재귀적인 방법으로 풀어냈었지만, 넓이 우선 순회는 같은 수준의 노드들을 방문해야 되기 때문에, 재귀적인 방법은 쓰기가 어렵다.
"나중에 다시 방문하기로 하고 그 순서를 기억해 두자"
- 먼저 넣은 원소가 먼저 나오는, 선입선출 (FIFO) 성질을 가지고 있는 큐를 이용한 응용
낮은 수준부터 훑어가듯이 순회를 하게 된다.
같은 수준의 노드의 경우, 왼쪽부터 오른쪽 순으로 방문하기로 한다.

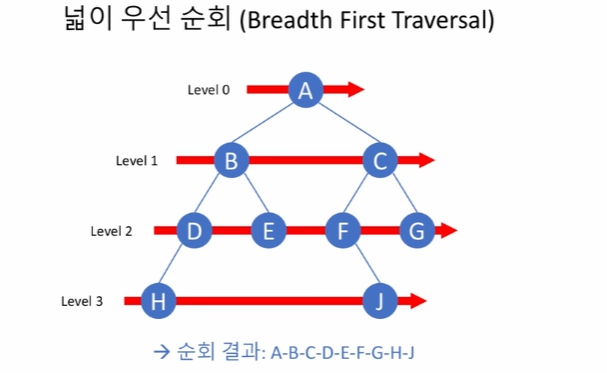
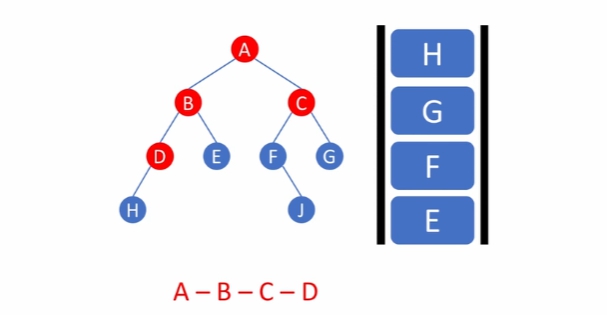
level 순서대로 왼쪽 -> 오른쪽 순서로 방문한다
나중에 방문할 노드드를 차례로 기억해야한다.
B를 방문했을 때 D, E를 기억해놓고, C를 방문했을 때, F, G를 방문하는 식이다.
C 까지 방문하면 큐의 방식대로 D를 방문하는 데, 이때에 H를 기억해 놓는다.
이 순서라면 결과적으로 넓이 우선 순회가 가능하다

넓이 우선 순회 알고리즘 설계
A 노드에 방문할 때, 각각 자식이 있다면, B, C를 큐에 저장
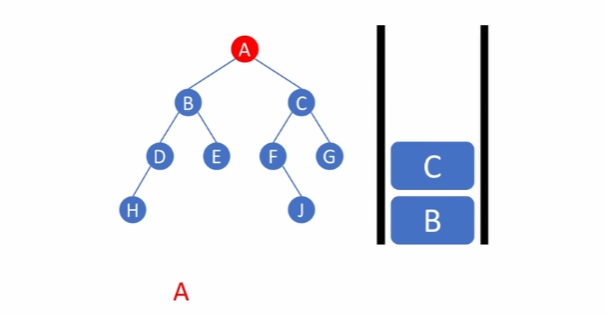
B를 방문했을 때, 각각 자식 노드를 저장
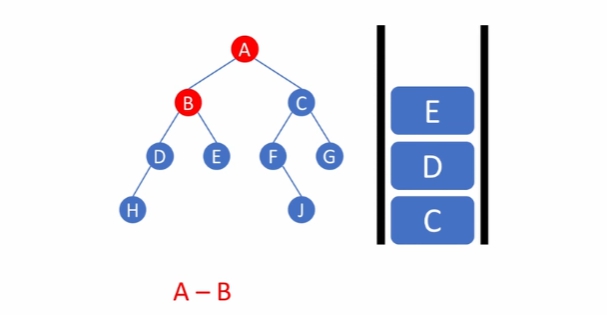
C를 방문하고, 자신의 왼쪽, 오른쪽 자식이 있으면 자식들 저장
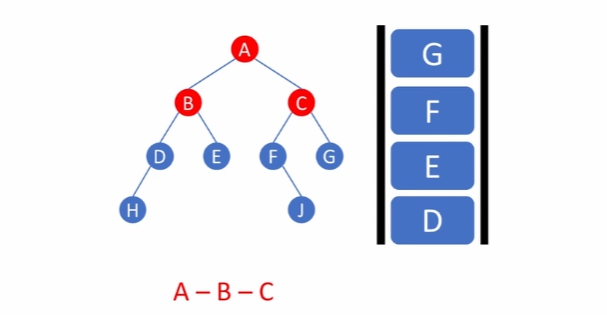
level 1 방문을 마치게 되면, 큐에는 level 2 노드가 순서대로 저장되어 있다
노드 E의 경우 자식이 없기 때문에, 그대로 처리를 종료, F의 경우 J 자식이 있기 때문에 다시 큐에 집어 넣음
level 2도 방문을 마치면 큐에는 level 3 노드가 순서대로 저장되어 있음.
level 3 방문 시엔, 자식 노드들이 없으므로, 그대로 처리를 종료한다.
결과적으로 모든 노드들을 방문하고 종료하게 된다.
넓이 우선 순회 알고리즘 구현
빈 트리는 할 일이 없음. root node 존재 시에 q를 쓰기 시작

연습 문제
내 풀이
class ArrayQueue:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self, r):
self.root = r
def bft(self):
traversal = []
q = ArrayQueue()
if self.root:
q.enqueue(self.root)
while q.isEmpty() != True:
node = q.dequeue()
traversal += node.data
if node.left:
q.enqueue(node.left)
if node.right:
q.enqueue(node.right)
else:
return []
return traversal
def solution(x):
return 0어려웠던 점.
처음 루트 노트가 없을 시 리턴값을 0으로 했더니 테스트 1 실패, 이후 빈 리스트 [] 로 반환했더니 성공. 좀 더 꼼꼼하게 문제를 읽는 습관을 길러야 한다.
