학습 주제
이진 트리

학습 내용
이진 트리의 정의
이진 트리 구현

이진 트리는, 트리에 포함되는 모든 노드의 차수가 2 이하인 트리를 말합니다. 즉, 모든 노드는 자식이 없거나 (리프 노드의 경우), 하나만 있거나, 아니면 둘 있는 세 경우 중 하나에 해당합니다.

우선은, 이진 트리를 추상적 자료 구조로 구현하기 위해서, 아래와 같은 연산을 생각해봅니다.

size() - 현재 트리에 포함되어 있는 노드의 수를 구함

depth() - 현재 트리의 깊이 (또는 높이) 를 구함

트리는 정의 자체가 재귀적이기 때문에, 이를 대상으로 하는 연산들도 대부분 재귀적으로 구현 가능합니다. 위 두 가지의 간단한 연산을 위한 코드를 살펴보고 연습문제로도 풀어봄으로써, 재귀적인 자료 구조가 (특히 트리가) 이러한 성질에 근거하여 얼마나 쓸모가 있게 되는지를 짐작해보시기 바랍니다.

트리의 각 노드를 정해진 순서로 방문하는 것을 순회 (traversal) 연산이라고 부릅니다. 트리를 순회하는 순서를 크게 나누면 깊이 우선 순회 (depth first traversal) 와 넓이 우선 순회 (breadth first traversal) 가 있습니다. 이 순회 방식들은 - 지난 강의에서 언급했듯이 우리 강의에서는 나아가지 않지만, 보다 일반적인 형태인 - 그래프에도 적용되는데, 많은 알고리즘들이 트리 또는 그래프의 순회를 이용하여 주어진 문제를 해결합니다.

이 중, 깊이 우선 순회가 보다 간단하므로 여기에서는 깊이 우선 순회를 먼저 알아보고, 다음 강의 (제 19 강) 에서 넓이 우선 순회도 알아봅시다.

깊이 우선 순회에도, 특히 이진 트리를 대상으로 하는 경우에는, 세 가지의 서로 다른 순서를 정의할 수 있습니다. 어느 노드 x 를 기준으로 할 때, (이 정의는 또 다시 재귀적임을 발견하세요)

중위 순회 (in-order traverasl): 왼쪽 서브트리를 순회한 뒤 노드 x 를 방문, 그리고 나서 오른쪽 서브트리를 순회

전위 순회 (pre-order traversal): 노드 x 를 방문한 후에 왼쪽 서브트리를 순회, 마지막으로 오른쪽 서브트리를 순회

후위 순회 (post-order traversal): 왼쪽 서브트리를 순회, 오른쪽 서브트리를 순회, 그리고 나서 마지막으로 노드 x 를 방문

하는 순서입니다. 이러한 순회 알고리즘 또한 (정의에서 느껴지는 바와 같이, 당연히) 재귀적으로 구현하는 것이 매우 자연스럽습니다. 중위 순회 알고리즘을 예제 코드로 보였습니다. 아주 조금만 바꾸면 나머지 둘, 즉 전위 순회와 후위 순회를 구현할 수 있습니다. 이 두 알고리즘은 연습문제로 풀어보세요.

이진 트리의 경우 자식의 노드가 최대 2개라 구현하고, 알고리즘을 생각하기가 쉬운 편.
다른 형태의 트리도 충분히 구현 가능

구현은 대부분 재귀적으로 이루어 지기 때문에 재귀적인 기능을 염두에 두고 짤 것

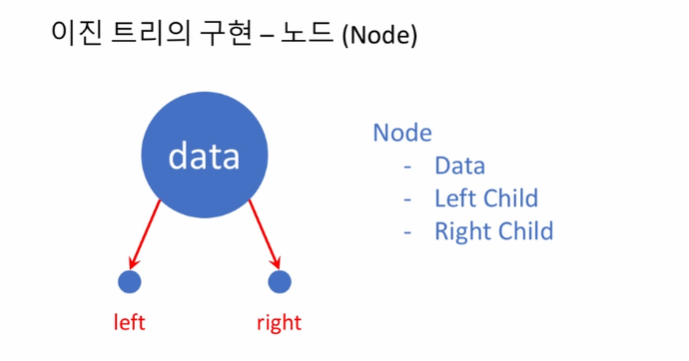
각 자식 노드를 가리키는 포인터를 가짐

연결 리스트 생성과 비슷한 면이 있다

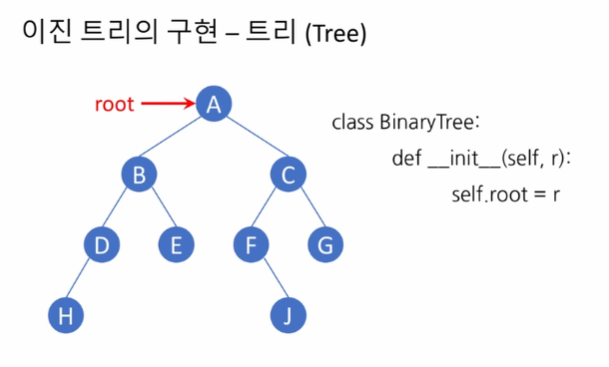
root 노드만 가르키고 있으면, 모든 노드가 간선으로 이어져 있기 때문에

연결 리스트의 head 처럼 시작 부분을 알리는 위치

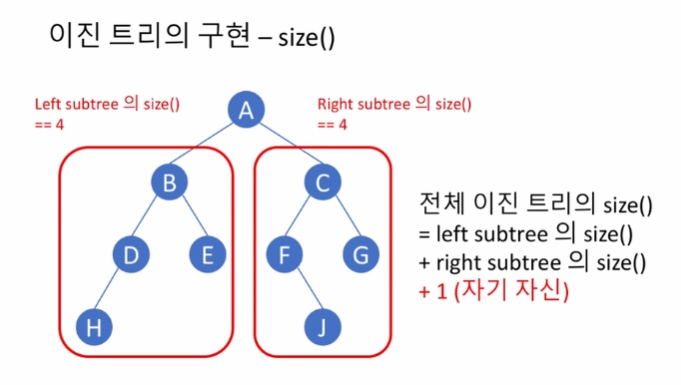
size() 함수도 왼쪽, 오른쪽 자식 노드에서의 size() 호출시키는 식으로 재귀적으로 구성된다.
왼쪽 자식노드에서 size() 함수 호출 시, 다시 자식 노드의 자식에서도 size() 호출이 이루어진다.
주의할 점으로 자기 자신도 노드이기 때문에 꼭 + 1을 해줘야 한다.
보통 코드를 짜다 보면 범위, 크기에서 +1 여부로 코드가 구현이 안되곤 한다.

# 두줄 코드를 한 줄 코드로 작성
if self.left:
	l = self.left.size()
else:
	l = 0
    
l = self.left.size() if self. left else 0 

노드 입장에서 자기 자신을 기준으로는 root이고, 사이즈를 리턴함 => 코드 짜면서 다시 확인 필요

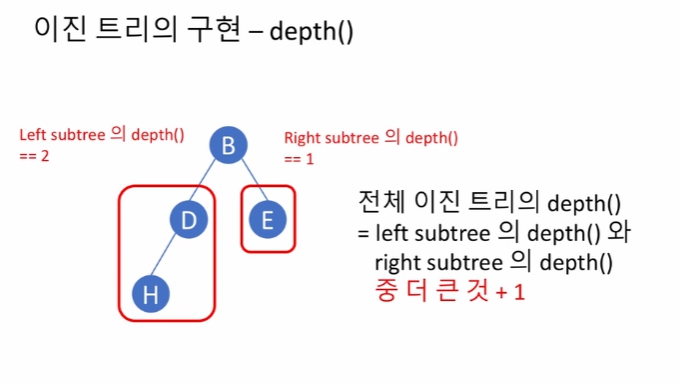
depth() 도 마찬가지로 자신의 자식 노드의 depth()를 재귀적으로 반환받아 그 중 큰 것 +1 (+1의 이유는 자기 자신이 포함됨으로 depth 가 1 늘어났기 때문)

clas BinaryTree에서 마찬가지로 자신이 empty 인지 확인 한 후, Node의 depth를 호출하는 식으로 깊이를 구함

순회 (Traversal)

정해진 순서는

• 깊이 우선 순회 (depth first traversal)

• 넓이 우선 순회 (breadth first traversal)

• 깊이 우선 순회는 다시,
  - 중위 순회 (in-order traversal)

  • 전위 순회 (pre-order traversal)
  • 후위 순회 (post-order traversal)
    가 있다.

  이번 강의 때는 깊이 우선 순회를 먼저 배운다

  자기 자신 노드를 '언제' 방문하는지에 따라 중위 전위 후위라 한다

  

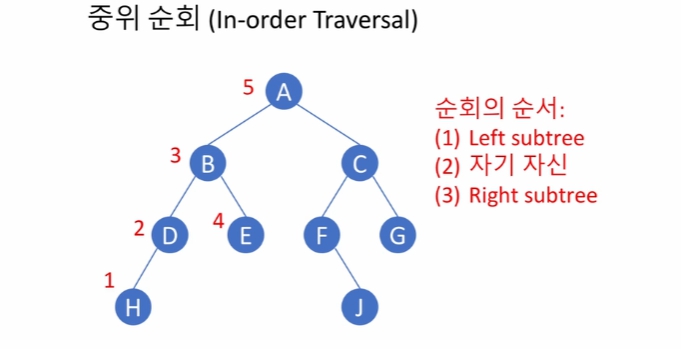
중위 순회의 경우 left subtree 방문, 자기 자신, right subtree 방문이다. 없을 시에는 방문하지 않으며, A 입장에서 E 까지 순회를 돌고 나면, 자신의 left subtree가 모두 순회를 돌았기 때문에, 자기 자신을 순회하고, C로 넘어가 right subtree 순회를 시작한다.
A 입장에서 C는 right subtree 지만, C에서 순회를 시작한다고 했을 때는 다시 left subtree 순으로 순회를 시작해야 한다.

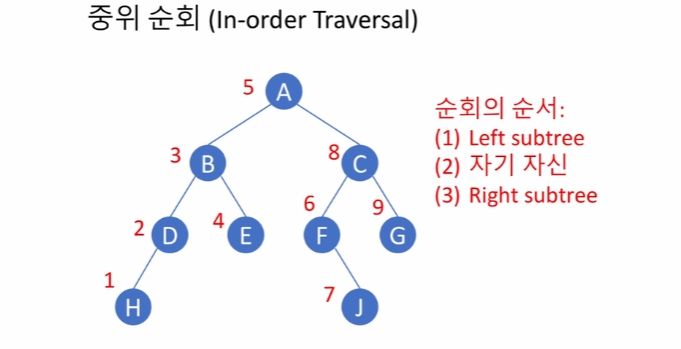
F 에선 left subtree가 없기 때문에 그 다음 순서인 자기 자신이 순회된 것을 확인 할 수 있다.
최종적으로 G 까지 순회를 마친 뒤에는 A 입장에서 right subtree의 순회도 마쳤기 때문에, 모든 순회를 마쳤다고 할 수 있다.

코드로 구현했을 때 별도의 순회 메서드를 생성하고, 리턴 값은 리스트이기에 빈 리스트 생성,
코드 순서를 보면 왼쪽을 탐색, 자기 자신 탐색, 그리고 오른쪽을 탐색하는 모습을 볼 수 있다.

자기 자신은 바로 append 가능한 이유는, 최초 루트 노드에서 자기 자신은 1개가 무조건 있기 때문이다.

Node.inorder()를 class에서 접근하이 위해, inorder를 생성해, 빈 노드가 아니면 순회를 돌게끔 하였다.

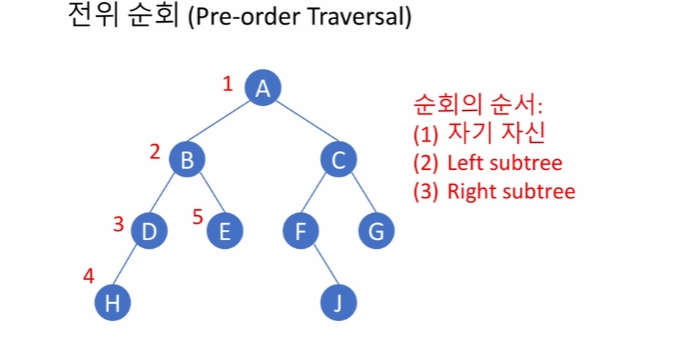
B 입장에서 자기 자신, 왼쪽 순회가 끝나 비로소 E를 순회

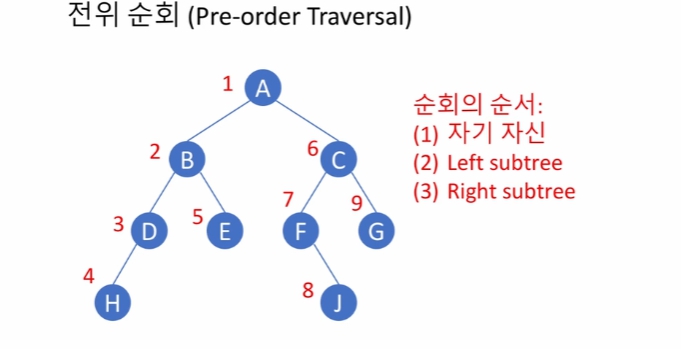
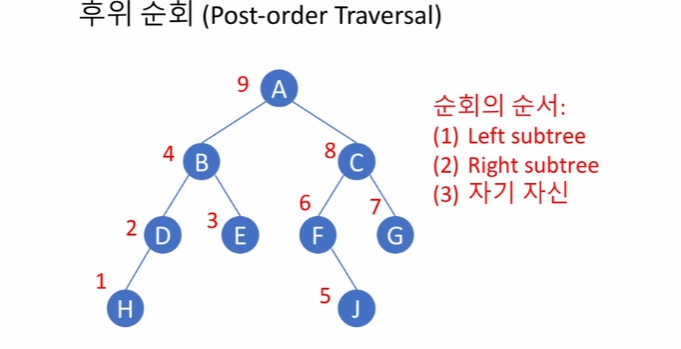
A 입장에서 후위 순회의 순서는 B가 순회, C가 완전히 순회되는 것이다. C는 다시 F가 순회되어야하고, F는 left subtree가 없기에 그 다음인 J, 자기 자신 순회가 되었다. C 입장에서 left subtree가 순회되었으므로, G, C, 마지막으로 A 입장에서 left, right가 모두 순회되었으므로 마지막으로 자기 자신이 순회 되었다.

연습 문제

이진 트리의 depth() 구현, 빈칸채우기

내 풀이

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None


    def size(self):
        l = self.left.size() if self.left else 0
        r = self.right.size() if self.right else 0
        return l + r + 1


    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        return max(l, r) + 1


class BinaryTree:

    def __init__(self, r):
        self.root = r

    def size(self):
        if self.root:
            return self.root.size()
        else:
            return 0


    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0


def solution(x):
    return 0

어려웠던 점.
depth의 l, r 만들 때

l = self.left.depth() if self.left() else 0
r = self.right.depth() if self.right() else 0

이렇게 괄호를 입력하니 계속 안되는 실수를 했다. 테스트 1이 통과해버려서 정말 맞는 답인줄 알고 숫자를 잘못썼나 계속 계산했는데, 너무 어이없는 실수였다. 이로써 테스트 케이스는 한 두개를 맞춰서 만족하는게 아니라, 다 맞추는 거를 기본으로 해야만 한다.

연습 문제

이진 트리의 전위순회 연산 구현

내 풀이

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None


    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        if self.right:
            traversal += self.right.inorder()
        return traversal


    def preorder(self):
        traversal = []
        traversal.append(self.data)
        if self.left:
            traversal += self.left.preorder()
        if self.right:
            traversal += self.right.preorder()         
        
        return traversal


class BinaryTree:

    def __init__(self, r):
        self.root = r


    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []


    def preorder(self):
        if self.root:
            return self.root.preorder()
        else:
            return []


def solution(x):
    return 0

단순히 위치만 옮기면 되었다.

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None


    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        if self.right:
            traversal += self.right.inorder()
        return traversal


    def postorder(self):
        traversal = []
        if self.left:
            traversal += self.left.postorder()
        if self.right:
            traversal += self.right.postorder()
        traversal.append(self.data)
        return traversal


class BinaryTree:

    def __init__(self, r):
        self.root = r


    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []


    def postorder(self):
        if self.root:
            return self.root.postorder()
        else:
            return []


def solution(x):
    return 0

하다보니, 프로그래머스에서 작업하다보면 단어를 잘못 쓰거나, 띄어쓰기 등 실수를 해도 인지하지 못하는 경우가 많다, vs code로 넘어가 작업하는게 나아보인다.