학습 주제
최대 힙 (Heaps) 에서 원소 삭제

학습 내용

앞선 제 21 강에서 경험했던 것처럼, 노드의 삭제는 삽입보다 다소 복잡합니다. 최대 힙 (max heap) 의 경우에도 그렇습니다. 이번 강의에서는 지난 강의 (제 22 강) 에서 정의한 최대 힙의 추상적 자료 구조에 원소 (노드) 의 삭제 연산을 추가해보겠습니다.
최대 힙에서의 원소 삭제는 항상 루트 노드에서 이루어집니다. 최댓값을 순서대로 뽑아 내는 데 관심이 있기 때문입니다. 이 연산을 반복 적용함으로써 데이터 정렬을 구현할 수 있다는 점은 이미 지난 강의 (제 22 강) 에서 설명한 바 있습니다. 그런데, 루트 노드를 삭제하고 나면 트리의 구조를 다시 정리해야 합니다. 앞서 (제 22 강에서) 언급한 것처럼, 노드의 삭제 또한 맨 마지막 노드에서만 일어납니다 (완전 이진 트리의 성질을 만족해야 하므로). 즉, 우선은 루트 노드의 데이터를 꺼내고, 맨 마지막 노드의 원소를 루트 노드의 자리에 임시로 집어넣습니다. 그 후, 마지막 노드를 제거한 다음에 루트 자리에 임시로 들어간 노드의 새로운 올바른 자리를 찾아 주면 됩니다.
노드의 삽입 연산에서와는 반대로, 이번에는 임시로 들어간 (일시적으로 위치가 올바르지 않은) 노드는 루트 노드에서 시작해서 아래로 아래로 내려갑니다. 자식들 중 더 큰 값을 가지는 노드와 자리를 바꾸면서, 더이상 바꿀 필요가 없거나 리프 노드에 도달할 때까지 이 과정을 반복합니다.
물론 이 자리 바꿈은 트리의 본질적인 성질에 기인하여 재귀적으로 구현될 수 있습니다. 그런데, 어느 노드에서 이 자리 바꿈을 행할 때의 코드 구현이 삽입의 경우보다 조금 복잡합니다. 왜냐면, 노드의 삽입에서는 자신의 부모 노드를 찾아서 자리를 바꿀지를 결정하는데 부모 노드는 오직 하나만 있거나 아니면 없는 (루트 노드의 경우) 데 비하여, 삭제 연산에서는 자식들 중 더 큰 키 값을 가지는 노드를 찾는데 자식이 둘 있는 경우, 하나만 있는 경우, 아니면 없는 경우 (리프 노드) 의 세 가지를 구별해서 생각해야 하기 때문입니다.
하지만 겁먹을 필요는 없습니다. 이미 우리는 (이 강의가 마지막 강의입니다) 코드 구현 연습을 꽤 탄탄하게 했고, 동영상 강의에서는 이 알고리즘을 보다 상세하게 설명합니다. 또한, 연습문제는 (그래도 조금 복잡하게 느껴지므로) 빈 칸 채우기 형태로 되어 있습니다.
마지막으로, 최대 힙을 이용하면 데이터의 정렬 이외에도 제 16 강에서 소개한 우선 순위 큐 (priority queue) 를 효과적으로 구현할 수 있음을 생각해보세요. Enqueue 할 때 "느슨한 정렬" 을 이루고 있도록 하고 (데이터를 완전히 순서대로 나열한 것과는 조금 다르죠?) dequeue 할 때 최댓값을 순서대로 꺼낼 수 있으며, 이 두 연산은 모두 (데이터의 개수가 n 이라고 할 때) log(n) 에 비례하는 복잡도를 가집니다.

최대 힙에서 원소의 삭제

특징을 위주로 확인

• 뺀 뒤에도 완전 이진 트리를 유지해야 함 -> 우리가 할 일
• 마지막 자리 노드 (배열로 마지막 인덱스에 위치) 를 임시로 루트 노드의 자리에 배치
• 임시로 완전 이진 트리를 생성
• 임시 노드를 자식 노드들과 비교해서 교체하여 더 큰 자식이 있을 때, 그 노드와 자리를 바꿔가며 아래로 이동
• 삽입 시 -> 부모 노드 1개만 비교, 삭제 시 -> 자식노드 2개 중 더 큰 값.

최대 힙에선 최대 원소를 삭제하라는 요청 밖에 없음.



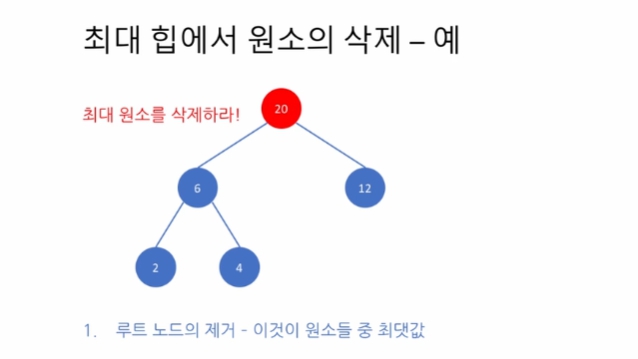
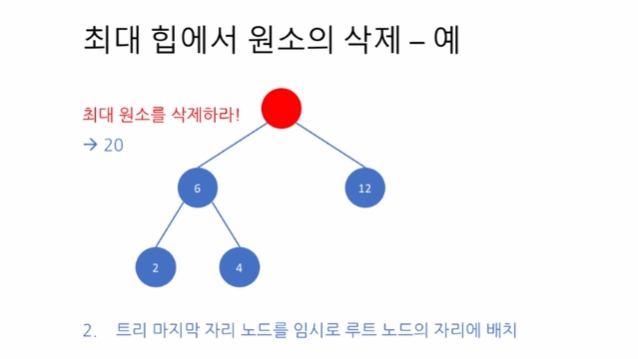
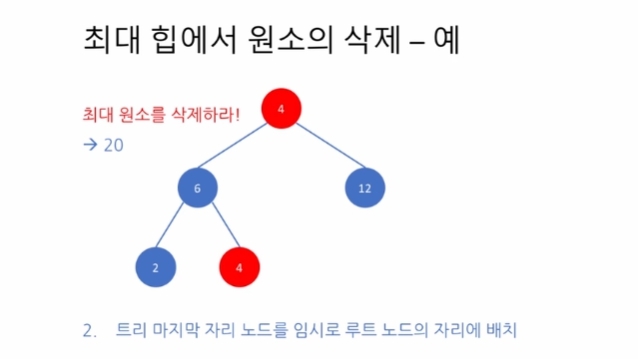
마지막 노드를 임시로 루트 노드에 배치

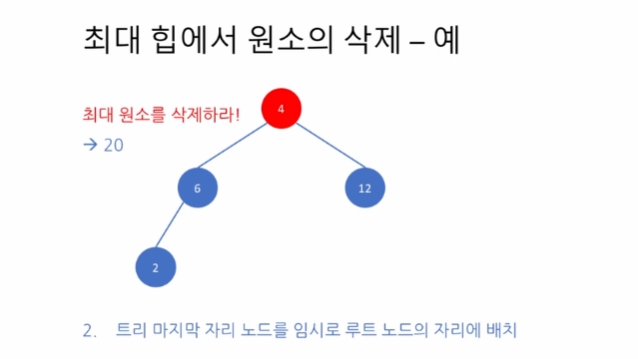
끝 노드를 삭제. 완전 이진 트리가 유지되는 모습이다.
그러나 루트 노드 4가 자식들과 비교해서 제일 크지 않다. (최대 힙의 성질)

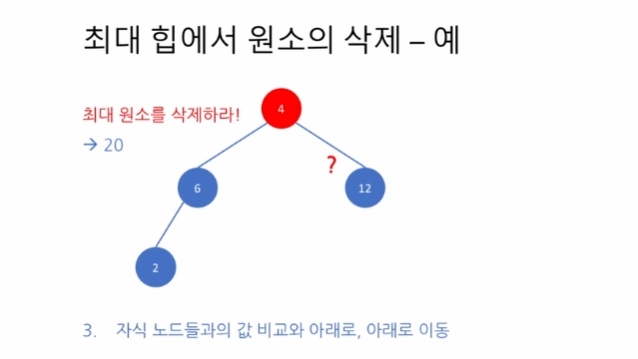
이 때 루트 노드의 자식들의 키 값은 6, 12 인데 우리는 12를 골라야한다 왜냐하면, 6이 루트로 올라오게 되면 오른쪽 자식인 12보다 작게 되어 최대힙 성질을 만족하지 못하기 때문이다.
그럼 12 가 올라왔을 때는? 6은 subtree 에서 자체 최대 힙이므로, 6보다 크기만 하면 12는 루트 노드로 올라간 뒤에도 최대 힙을 유지하게 된다.
-> 따라서 자식들 중 더 큰 key 값을 가지는 자식과 위치를 바꾼다

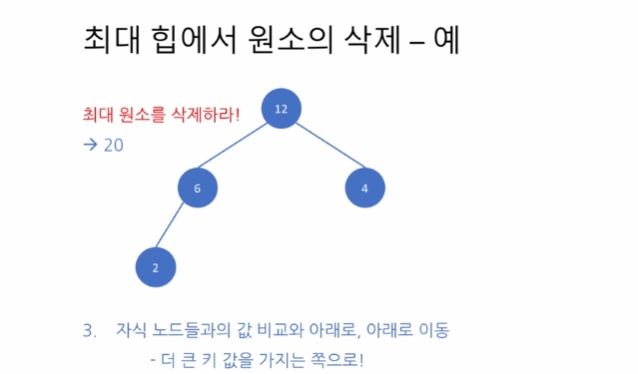
노드 6 아래는 여전히 최대 힙의 성질을 유지하고 있다. 오른쪽 자식으로 내려간 4 아래에 subtree가 있다면 재귀적으로 위치 교환을 해 나가면 된다.

자식 노드들과는 logn(최대 높이) * 2(자식 2개 모두 비교할 경우)
2는 무시하게 됨 Big-O 에선

우선 배열의 갯수가 1 이상인지, 0 인덱스는 버리기 때문.. 1개 이상의 노드가 있어야함

• 1. 루트 노드, 마지막 노드 값 교환
• 2. 마지막 노드 제거 pop(-1), 그냥 pop() 해도 마지막임
• 3. maxHeapify(1) 루트 노드 부터 시작해서, recursive하게 구현
     

maxHeapify() 구현 -> 연습문제에서 구현

smallest = i, 자기 자신으로 초기화 해서 비교해 나감.
인덱스를 smallest에 담음

재귀적으로 호출해 나가면서 찾아감
if smallest != i: -> 재귀 조건, (왼쪽, 오른쪽 구분이 없음. 간결한 코드)

자기 자신이 최대치를 가짐. leaf 노드 포함이기 때문에, 왼쪽, 오른쪽 자식이 있는지도 확인하는 조건문이 필요.

최대/최소 힙의 응용

1. 우선순위 큐
   

2. 힙 정렬
   
   삭제(정렬)를 n 번하기 때문에 복잡도는 O(nlogn)
   디큐를 모두 하게 된 결과는 정렬된 결과임.
   
   힙이 비지 않을 동안 계속 반복

연습 문제

내 풀이

class MaxHeap:

    def __init__(self):
        self.data = [None]


    def remove(self):
        if len(self.data) > 1:
            self.data[1], self.data[-1] = self.data[-1], self.data[1]
            data = self.data.pop(-1)
            self.maxHeapify(1)
        else:
            data = None
        return data


    def maxHeapify(self, i):
        # 왼쪽 자식 (left child) 의 인덱스를 계산합니다.
        left = i * 2

        # 오른쪽 자식 (right child) 의 인덱스를 계산합니다.
        right = i * 2 + 1

        smallest = i
        # 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if left < len(self.data) and self.data[left] > self.data[i]:
            # 조건이 만족하는 경우, smallest 는 왼쪽 자식의 인덱스를 가집니다.
            
            smallest = left

        # 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if right < len(self.data) and self.data[right] > self.data[smallest]:
            # 조건이 만족하는 경우, smallest 는 오른쪽 자식의 인덱스를 가집니다.
            
            smallest = right

        if smallest != i:
            # 현재 노드 (인덱스 i) 와 최댓값 노드 (왼쪽 아니면 오른쪽 자식) 를 교체합니다.
            
            self.data[i], self.data[smallest] = self.data[smallest], self.data[i]

            # 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리합니다.
            self.maxHeapify(smallest)


def solution(x):
    return 0

MH = MaxHeap()
MH.data += [50,25,6,3,17,2,5]
print(MH.remove())
print(MH.data)

어려웠던 점.
자식이 존재하는지 확인하는 기준으로

		# 처음
        if self.data[left] and self.data[left] > self.data[i]:
        
        # 개선
        if left < len(self.data) and self.data[left] > self.data[i]:

계속 out of range 배열을 벗어났다고 하는 것이다. 처음에 내가 부등호를 잘못 했나 하고, 파이썬 튜터를 돌렸는데 파이썬 튜터에서는 또 결과를 출력해줬다. vs code에선 계속 에러가 났고. 배열의 경우 없는 인덱스에 접근하려는 순간 바로 에러를 출력하기 때문에, left 숫자가 전체 데이터 숫자 안에 있는지 확인하는 식으로 해야한다. 정말 기초적인 실수였다.