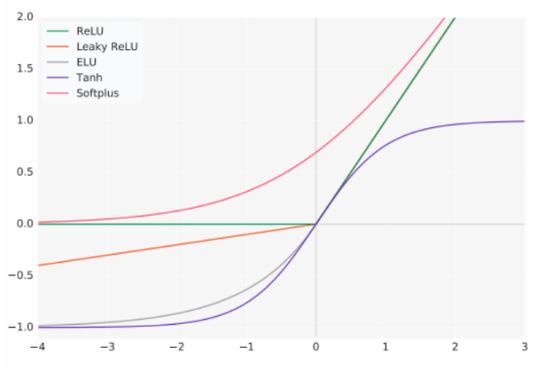
활성함수 activation function
활성함수는 ANN의 출력 결과 값을 변환하여 다른 뉴런에 전달하는 역할을 합니다.활성함수는 ANN의 출력값을 다른 뉴런에 전달한다는게 이해가 안갈수도 있습니다.
왜 변환하여 전달할까요? 왜 값을 변환하여야만 할까요?
활성함수의 이해
y = ax + b == f(x) = ax + b
라는 1차 방정식이 있습니다.
그래프로 그리면 아래와 같이 나타납니다.
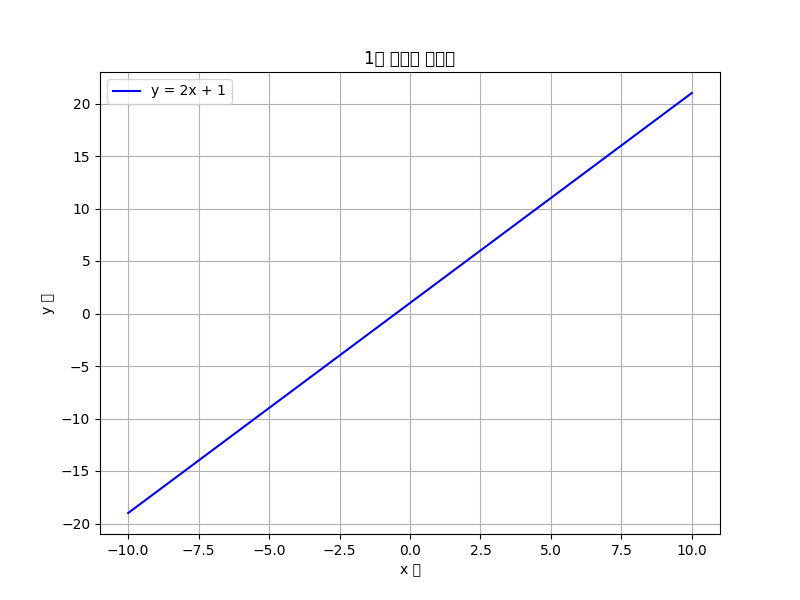
만약에 저함수에 f(x) = ax라는 활성함수를 도입해보겠습니다.
import numpy as np import matplotlib.pyplot as plt m = 2 # 기울기 b = 1 # y 절편 x = np.linspace(-10, 10, 100) # -10에서 10까지 100개의 점 생성 y = m * x + b y2 = m * y plt.figure(figsize=(8, 6)) # 그래프 크기 설정 plt.plot(x, y, label=f'y = {m}x + {b}', color='b') # 첫 번째 그래프 그리기 plt.plot(y, y2, label=f'y2 = {m}y + {b}', color='r') # 두 번째 그래프 그리기 plt.xlabel('x 축') # x 축 레이블 plt.ylabel('y 축') # y 축 레이블 plt.title('1차 방정식 그래프') # 그래프 제목 plt.legend() # 범례 표시 plt.grid(True) # 그리드 표시 plt.show()
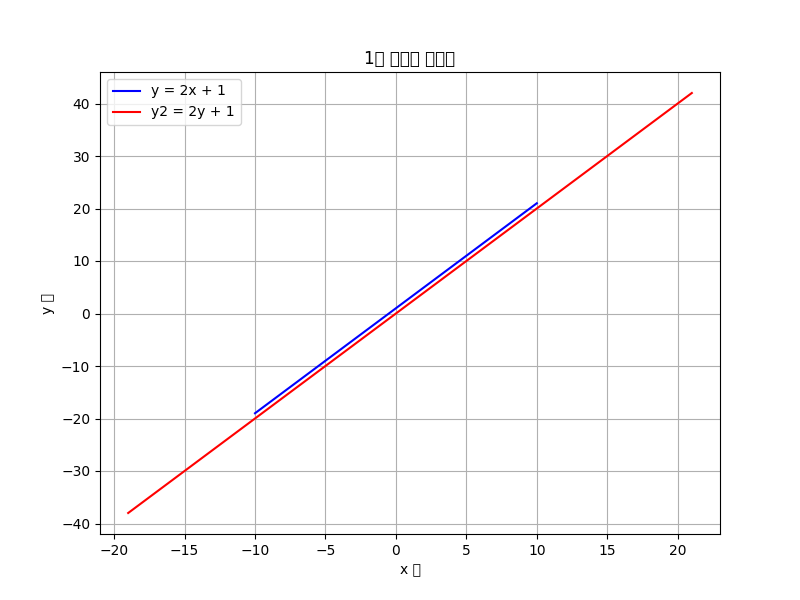
결국 선이 서로 겹치고 말았습니다....
그러면 수식으로 확인해봐요
1계층 f(x) = ax
2계층 f(f(x)) = a(ax)
3계층 f(f(f(x))) = a(a(ax)) = a^3*x결국 선이 계속 겹치게 됩니다.
그러면 비선형 함수로 모아 보겠습니다.
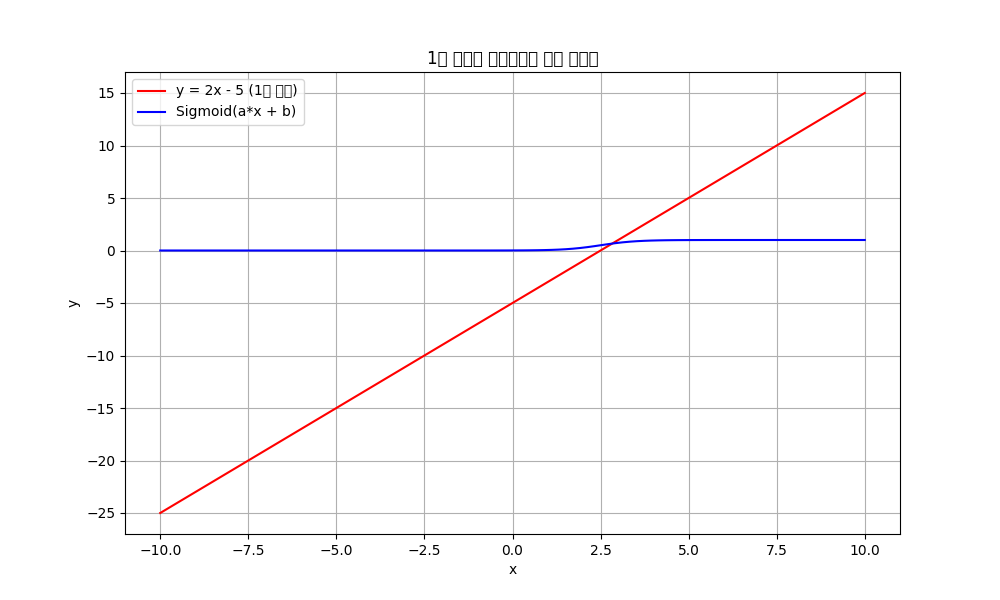
보아하니 값이 변화하였습니다.
만약에 선형 함수가 활성함수로 계속 이어진다면 결국 1계층 ANN과 다름 없습니다.
하지만 비선형 함수를 사용한다면 값이 변화하여 좀더 많은 값을 분류하거나 여러 사고를 할수 있는 계층을 쌓을수 있게 됩니다.
그렇기에 활성함수는 비선형 함수가 되어야합니다.
활성함수의 종류
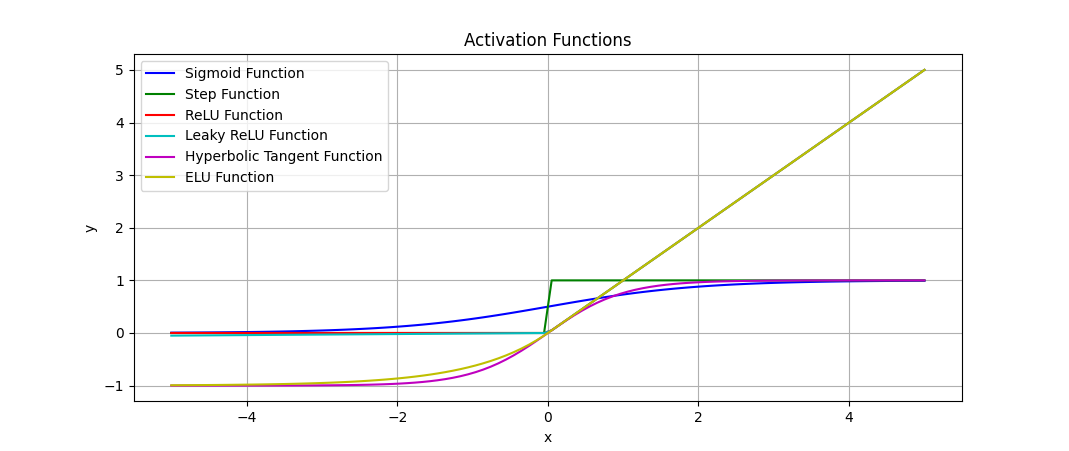
일단, 활성 함수의 종류를 보도록 합시다.
1. 계단 함수, step function
2. 시그모이드, sigmoid function
3. 하이퍼볼릭 탄젠트, Hyperbolic tangent
4. 렐루, ReLU
5. Leaky 렐루, Leaky ReLU
6. ELU, Exponential Linear Unit
계단 함수, Step Function
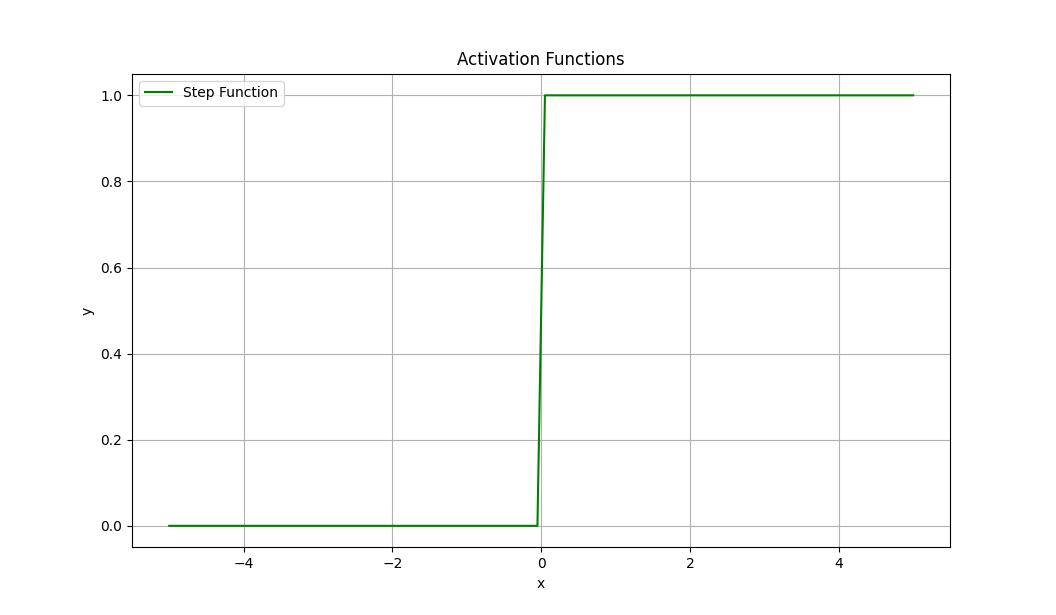
def step_function(x):
return np.where(x <= 0, 0, 1)
계단 함수는 0 or 1으로 표현됩니다.
임계값이상이면 1 임계값 미만이면 0 으로 나타나는 함수입니다.
그러한 점으로 비선형으로 함수를 바꿀수 있지만, 데이터 누실이 될 가능성이 높습니다.
시그모이드 함수, Sigmoid function
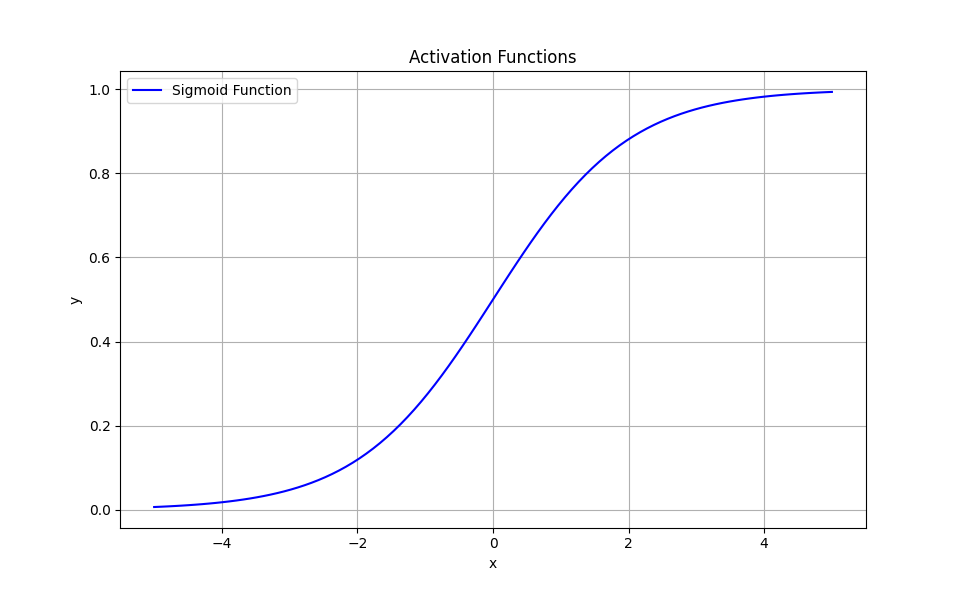
def sigmoid(x):
return 1 / (1 + np.exp(-x))시그모이드 함수는 완만한 선형의 형태를 가지고 있습니다.
그렇기에 계단 함수보다는 데이터 누실이 적습니다.
허나, 0에서 1이라는 작은 범위를 가지기에 입력값이 클수록 출력값이 0에 수렴하게 됩니다.
그러면 역전파를 하는 과정에서 기울기가 0이 되어버리는 기울기소실의 문제가 발생하게 됩니다.
하이퍼볼릭 탄젠트 함수 Tanh,Hyperbolic Tangent
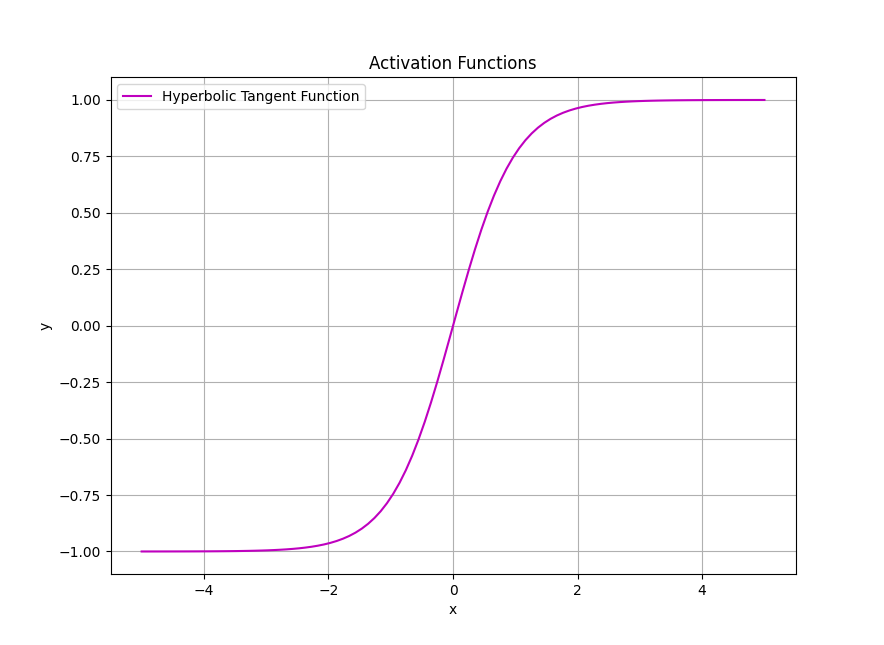
하이퍼볼릭탄젠트 함수는 시그모이드 함수의 진화형으로 보면 좀더 쉽게 다가 갈수 있습니다.
시그모이드 함수보다는 좀더 많은 범위값 (-1에서 1까지)의 범위를 가지기에 시그모이드 함수보단 기울기소실에 대한 영향이 적은 편입니다.
하지만 아직 기울기 소실이 해결되지는 않은 함수입니다.
렐루 함수 ReLU
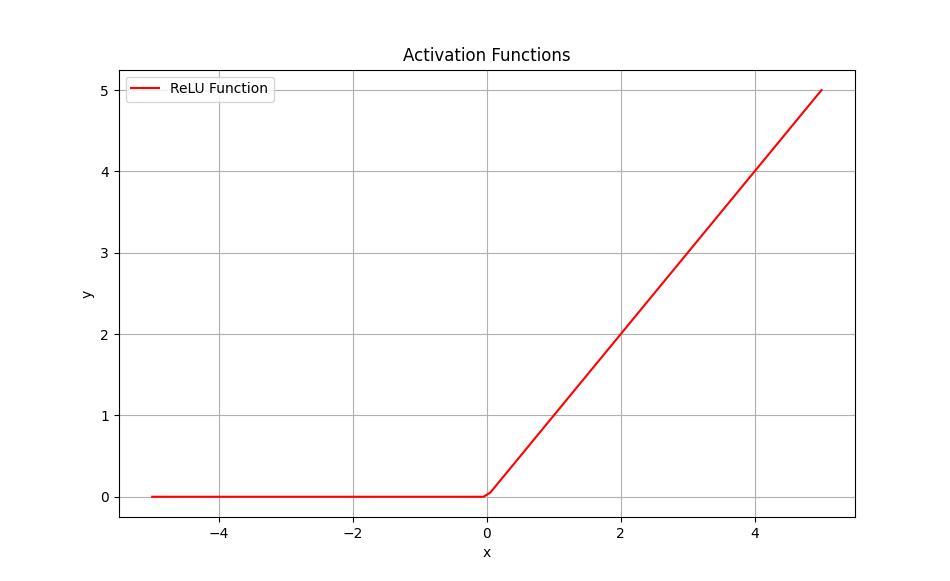
현대 딥러닝 분야의 가장 기초가 되는 함수입니다.
입력값이 0이면 0, 양수이면 그대로 표현하는 간단한 함수입니다.
다른 함수들과 다르게 기울기 소실에 문제가 해결된 함수입니다. 그렇기에 현대의 딥러닝에서 매우 중요한 문제를 해결한 함수라고 볼수 있습니다.
하지만, 0이하의 값은 모두 0으로 반환시키기 떄문에 음수에 대한 기울기는 표시할수 없습니다. 이러한 현상을 dying ReLU라고 표현합니다.
Leaky ReLU
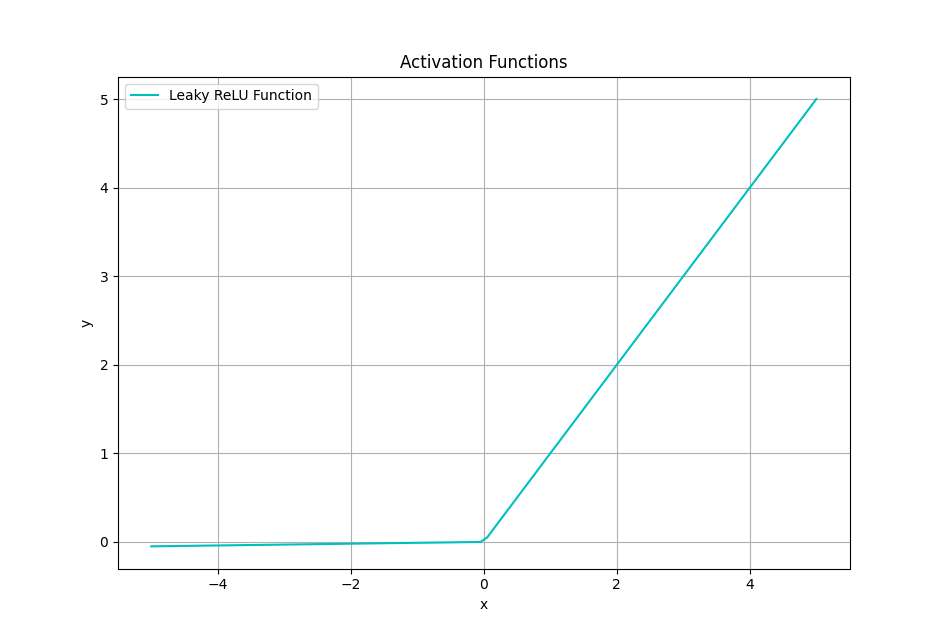
leaky ReLU는 기존 ReLU의 dying ReLU문제를 해결하는 함수입니다.
기존 ReLU함수에서 임계치 이하의 값에 0.01를 곱하여 해결한것입니다.
하지만, 기존 렐루함수보다 복잡한 계산을 해야하기 때문에 연산 비용이 더 들어갑니다.
소프트 맥스 함수 softmax
세 개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수입니다.
소프트맥스는 다른 활성화 함수와 다르게 출력층에서 항등함수와 같이 사용합니다.
정리
- 활성함수는 비선형 함수이여야한다.
- 활성함수로는 현재 ReLU함수를 가장 많이 사용하고 있다.
- 출력층에서는 softmax,sigmoid,항등 함수를 사용한다.
