데이터 분포를 학습해 결정경계(Decision boundary)를 만들어 데이터를 분류(classification)하는 모델
Bayes' Classifier(1)
베이즈 분류기(bayes' classifier)
-
사후확률 우도확률 * 사전확률
-
-
사후 확률값을 가장 크게 만들어주는 클래스로 분류하는 것
-
-
사전 확률 : 데이터가 k번째 클래스에서 뽑혔을 확률
-
Density funciton:
-
우도 확률 P(X|Y): 각 샘플이 i.i.d할 때, PDF(probability density function)의 곱과 동일
선형 판별 분석(linear discriminant analysis)
- 다음의 두 가지 가정을 사용함
- Density function이 Normal 혹은 Gaussian density를 따른다
--> : 평균, : 표준편차 - for all -->모든 표준편차가 같다.
--> X=x일때 Y=k클래스일 확률
판별 함수(discriminant function)
-
데이터 X=x를 분류하기 위해 판별 함수를 정의해야 함
-
판별 함수는 에 대한 값을 뱉는 함수
-
=
=
= -
두 번째 가정에 따라 quadratic 항을 삭제할 수 있어 선형 판별 함수를 갖게 됨
-
판별 함수
-
데이터를 통한 추정값 사용 --> 표본을 뽑아서 사용
-
- --> K클래스를 가진 데이터 / 전체 데이터
-
- --> 클래스 k를 가지는 데이터들의 평균
-
(cf. 통계적 추정을 할 땐 표본 자료 중 모집단에 대한 정보를 주는 독립적인 자료를 사용)
-
판별함수
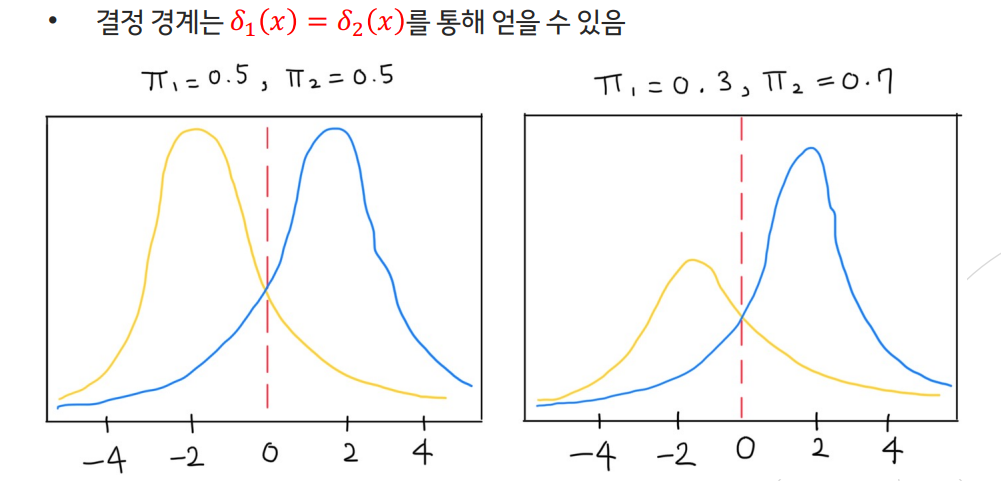

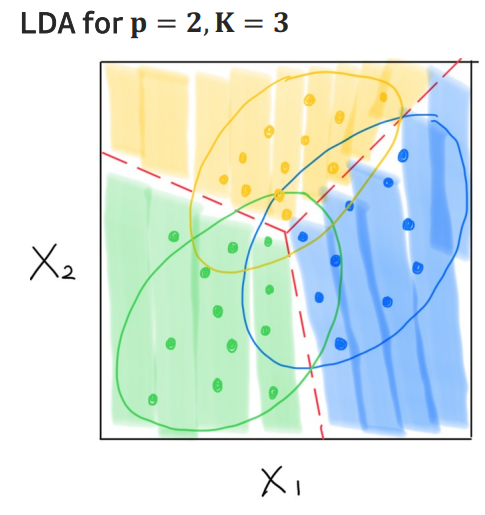

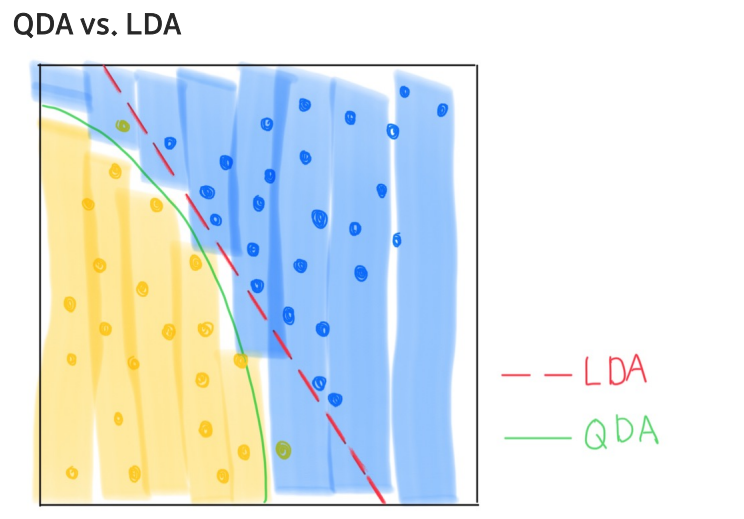
--> 데이터가 선형이나 비선형이냐에 따라서 QDA ,LDA의 성능이 다르기 때문에 데이터에 따른 알맞은 모델을 사용하는 것이 중요
--> 따라서 모든 모델의 개념을 알고 상황에 따라서 골라서 쓰는 능력이 중요하다.
