Ensemble Learning(앙상블 학습)

• 앙상블 학습은 여러 개의 모델을 학습시켜, 다양한 예측 결과들(평균, majority vote)를 이용하는 방법론
• 모든 머신 러닝 모델과 회귀, 분류 문제 모두에 적용 가능함
• 보통 결정 트리에서 자주 사용됨
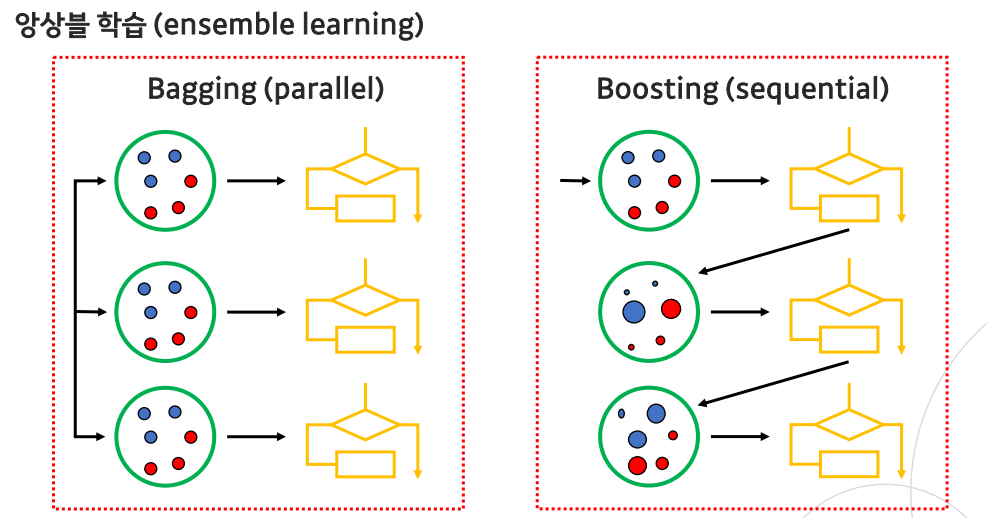
• 크게 Bagging과 Boosting 두 가지 방법론이 존재

부트스트랩(bootstrap)

• 모수(모평균, 모분산, 모비율, 모표준편차)의 분포를 정확히 추정하기 위해선 더 많은 표본 데이터셋이 필요함
• 하지만 표본을 계속 얻는 것은 현실적으로 어려움
• 현재 가지고 있는 샘플을 복원 추출(sampling with replacement)하여 여러 개(B개)의 데이터셋을 만듦
• $\sigma_\alpha = \sqrt{\frac{1}{B-1}\sum^B_{i=1}(\hat \alpha_i-\frac{1}{B}\sum^B_{j=1}\hat\alpha_j)^2}$
• $\frac{1}{B}\sum^B_{j=1}\hat\alpha_j$ : 평균
  
• 집합 내에서 중복되도 상관 없이 표본을 추출하는 복원 추출

부트스트랩 (bootstrap) with n obs

• j-th 샘플이 첫번째 bootstrap observation으로 뽑히지 않을 확률 : ($1-\frac1n$)
• j-th 샘플이 두번째 bootstrap observation으로 뽑히지 않을 확률 : ($1-\frac1n$)
• 전체 bootstrap 샘플에 j-th 샘플이 포함되지 않을 확률: $(1-\frac1n)^n$
• 데이터 개수 N이 충분히 많을 때 : $lim_{n\rightarrow\infin}(1-\frac1n)^n = \frac1e$
• B개의 bootstrap 데이터셋을 생성했을 때, j-th 샘플이 없는 데이터셋의 비율: $\frac1e =1/3$

Motivation of Bagging

• 각각 $\sigma^2$ 분산을 가진 n개의 독립적인 observation($Z_1,...,Z_n)$
• 관측의 평균 $\bar Z$에 대한 분산은 $\sigma^2/n$
• 여러 관측을 평균내면 분산을 줄여줌 --> 사용 이유
• 하지만 다수의 학습 데이터셋을 얻는 것은 현실적으로 어려움 --> 부트스트랩 사용

Bagging

• Bootstrap을 이용해, 한개의 학습 데이터셋으로부터 B개의 데이터셋을 추출
• 각가의 데이터셋으로 $\hat f^{*b}(x)$ 모델을 학습함
• 모든 예측치를 평균(회귀)내거나, majority vote(분류)를 취해 분산 오류를 낮춤
• 회귀 : $\hat f_{bag}(x) = \frac1B\sum^B_{b=1}\hat f^{*b}(x)$
• 분류 :$\hat f_{bag}(x) = argmax_k f^{*b}(x)$
• Bagging, 또는 Bootstrap aggregation이라 부르며, 보통 결정 트리(성능$\downarrow$속도$\uparrow$ 해석력$\uparrow$)에서 많이 사용
• 배깅을 사용하면,
  1. 결정 트리의 성능면에서의 단점을 보완 가능
  2. 학습 결과에 대한 해석력이 떨어짐.
• 특히, 어떤 피처(variable)가 가장 중요한지 판단이 힘듦
• B개의 결정 트리에서 각 variable에 따른 split으로 RSS(회귀) 혹은 Gini index(분류)의 감소량을 평균내 순위를 매김

OOB(Out-of-Bag Error Estimation)

• Bagged model을 사용하면 test error를 쉽게 추정할 수 있음
• 배깅은 bootstrap을 사용하기 때문에, 대략 2/3 샘플만으로 하나의 결정 트리를 학습
• 하나의 Bagged tree를 학습할 때 사용되지 않은 샘플들을 out-of-bag(OOB)로 부름
  
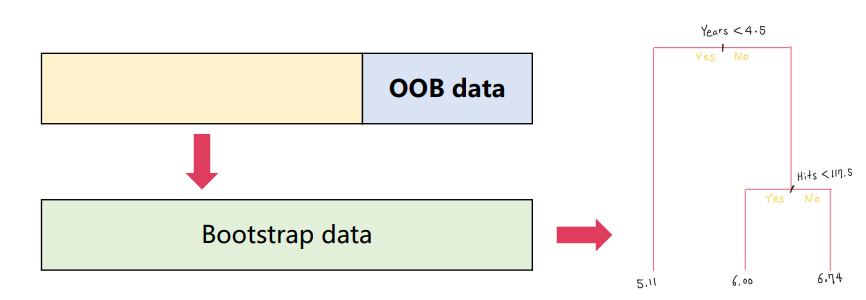
• OOB prediction : i-th 샘플이 포함되지 않은 bootstrap 데이터셋으로 학습된, 대략 B/3 개 tree들의 i-th 샘플에 대한 평균(회귀) 혹은 majority vote(분류)
• OOB error : 각 샘플들의 OOB prediction으로 얻은 오류
• OOB error는 test error에 대한 유효한 추정값이 됨
• B가 충분히 많을 때, OOB error는 LOOCV(교차검증)와 거의 동일함 --> OOB를 활용하여 교차검증

Random forests(랜덤 포레스트)

• Bagged tree 사이의 상관관계를 없애 성능을 향상시킨 알고리즘
• 원래는 p개의 variable을 모두 고려해 split을 결정해 결정 트리를 학습함
• 만약 강력한 variable이 있으면, B개의 모든 트리가 top split으로 이를 사용할 것임 --> 상관관계 커짐
• 상관관계가 커지면(=high Cov($\hat f^{*i},\hat f^{*j}$), 분산 오류가 크게 줄어들지 못함
• $Var(\bar Z) = \frac{Var(Z_1)+Var(Z_2)+2Cov(Z_1,Z_2)}{n^2}$
• P개의 variable 중 m 개를 랜덤하게 선택해 결정 트리를 학습함
• 상관관계가 줄어든 결정트리를 사용하기 때문에, 분산 감소 효과가 증폭됨
• 일반적으로 m = $\sqrt p$ 값을 사용할 때, 효과가 제일 좋음

Boosting

• 배깅과 마찬가지로, 다양한 알고리즘과 회귀와 분류 문제에 모두 적용 가능
• 결정 트리를 사용한 부스팅 알고리즘
  1. AdaBoost
  2. Gradient Boosting(GBM)
  3. XGBoost
  4. Light GBM
• 배깅은 병렬적으로 생성된 결정 트리를 앙상블하는 방법
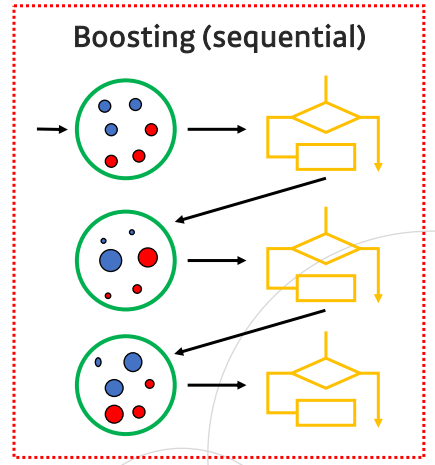
• 부스팅은 이전 스텝의 트리 정보를 활용해 순차적으로 (sequentially)트리를 만듦
  

하이퍼 파라미터

• Number of trees B :
  • 결정 트리를 순차적으로 생성할 때, 몇 개까지 생성할지 결정 --> 가중치가 쌓임
  • B값이 커질수록, over-fitting 문제가 발생함
• Number of split :
  • 각각의 결정 트리가 어느 정도의 depth를 가지는지 결정
  • Split이 한 번인(=2 terminal node) 결정 트리를 특별히 stump로 부름

AdaBoost

• 최초의 부스팅 알고리즘

• 이전 결정 트리가 잘못 예측한 데이터에 큰 가중치($w_1$)를 부여해, 다음 결정 트리가 더 집중할 수 있도록 순차적으로 학습

• 결정 트리로는 stump 구조 사용
  

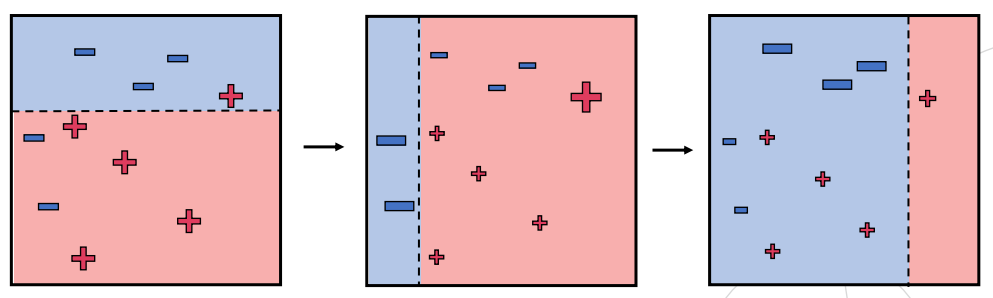
• B개의 결정 트리별로 계산된 모델 가중치($C_b$)를 합산해 최종 모델 생성
  

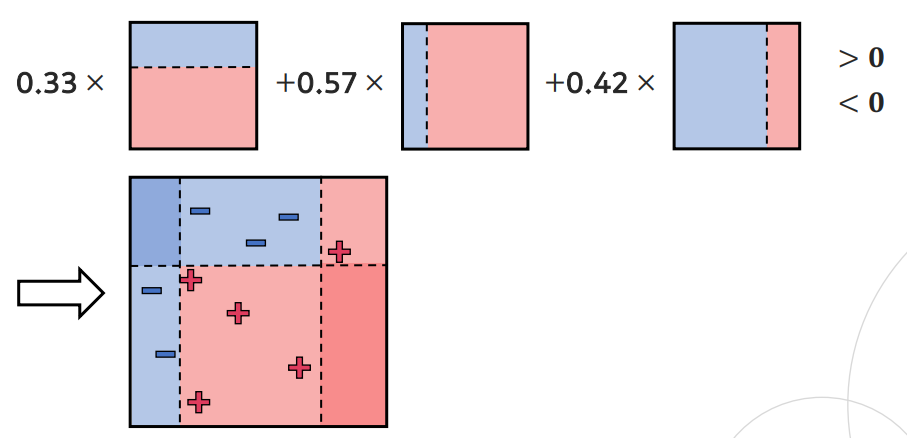
• b 번째 반복에서의 모델은 다음처럼 결정 트리의 선형 결합
  $\hat f_b(x_i) = c_1\hat f_1(x_i)+...+c_b\hat f_b(x_i)=\hat f_{b-1}(x_i) + c_b\hat f_b(x_i)$

• 손실함수는 지수 손실의 합으로 정의($w_i^1=1, w_i^b = e^{-y_i\hat f_{b-1}(x_i)}$가정)
  
  
  
  

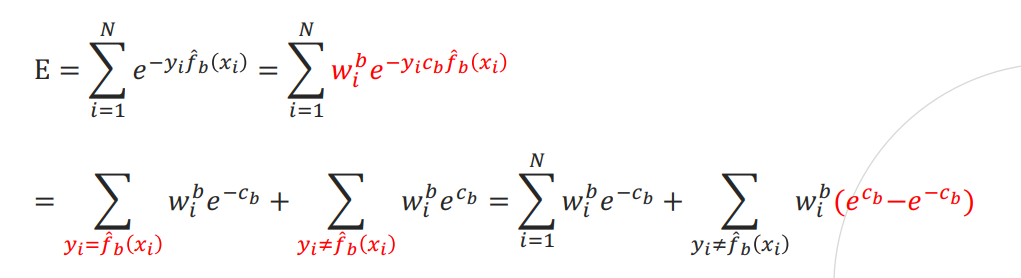
Gradient Boosting(GBM)

• 현재 모델의 오차(residual)를 줄이는 방향으로 결정트리를 학습하는 방법론
  
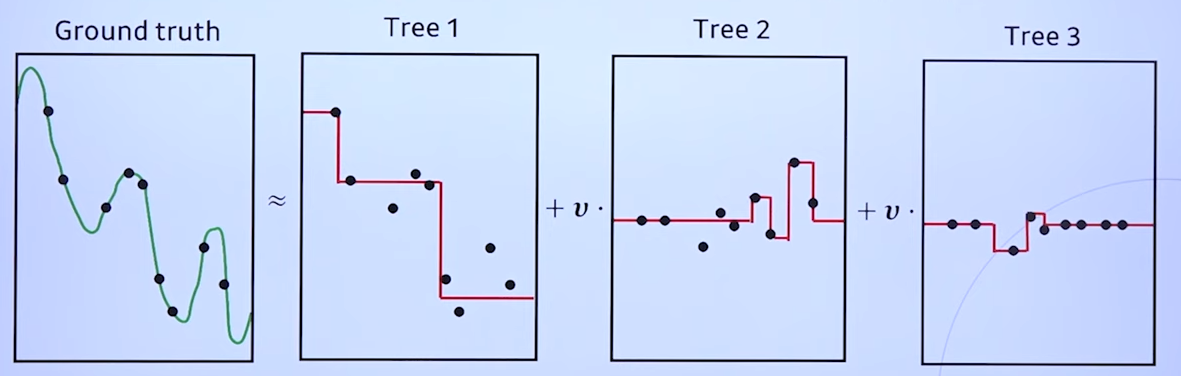
• 전체 샘플을 활용하되 가중치가 고려된 전체 데이터셋을 활용하여 학습 --> AdaBoost
• 오차가 생긴 샘플들에 한해서 학습을 하는 것 --> GBM
• 첫 번째 결정 트리는 하나의 leaf node 구조(=전체 데이터의 평균으로 예측)
• 이후에는 일반적으로 stump 보다는 더 복합한 트리 구조를 사용
• 손실 함수로는 보통 미분 가능한 MSE Loss, L1 loss, 혹은 Logistic loss사용
• Residual은 실제값과 예측값의 차이($y_i - \hat f(x_i)$)로, negative gradient와 같은 의미
• $\frac{\partial L}{\partial \hat f (x_i)} = \frac{\partial (y_i-\hat f(x_i))^2}{\partial \hat f (x_i)}=\hat f(x_i)-y_i$
• 정의한 손실 함수에 대한 negative gradient로 residual 계산
  --> 손실함수를 다양하게 사용할 수 있고, -gradient로 residual 계산
• 이전 모델의 residual을 최소화하는 결정 트리 $\gamma$ 학습(j는 terminal node 인덱스)
• $\gamma^b_j=argmin_{\gamma}\sum_{x_i\in R^b_j}L(y_i,\hat f_{b-1}(x_i)+\gamma)$
  
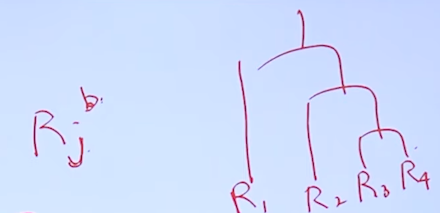
• 학습한 결정 트리를 그대로 합치면 over-fitting 문제가 발생할 수 있음
• 따라서, 학습률 하이퍼파라미터 $v$를 도입함 --> Adaboost의 $C_b$와 비슷
• $\hat f_b(x_i) = \hat f_{b-1}(x_i)+v\sum^{Jb}_{j=1}\gamma^b_j||(x \in R^b_j)$
• 경사 하강법 알고리즘과 동일

XGBoost

• GBM 알고리즘의 성능과 속도 면에서 향상된 알고리즘
• 기존의 GBM은 학습 데이터에 대한 residual을 계속 줄여 over-fitting 되기 쉬움
• 정규화 항을 손실 함수에 추가함($\gamma, \lambda$)
• $\Omega(f) = \gamma T + \frac12\lambda||c||^2$(T: terminal node의 수, c: 각 노드의 가중치)
• Split finding 알고리즘을 통해 연산의 효율성을 높임
  • 기존에는 모든 피처를 split 기준으로 탐색했었음
  • 이에 대한 근사 알고리즘을 제안해 속도를 향상시킴

Light GBM

• 기존의 boosting 알고리즘은 B번의 반복 학습 때마다 전체 데이터셋을 살펴봄
• 이 과정에서 대부분의 계산 비용이 발생함
• 결정 트리 학습에 사용되는 데이터 수를 다음의 방법들로 줄임
  1. GOSS(Gradient-based One-Side Sampling):
     작은 gradient 값을 가진 샘플들을 제외하는 방법론
  2. EFB(Exclusive Feature Bundling):
     상호 배타적(mutually exclusive)피처를 묶어, 탐색해야되는 피처 수를 감소시킴