8. 정렬
알고리즘 문제풀이에 허덕이고 주특기로 삼을 스프링 공부는 뒷전이 되어버린 요즘(...) 망했다고 하루에 몇 번씩 되뇌이는지 모르겠다. 하하하하하핳하하하핳 지금도 읊조리는 망했군 진짜 내일은 알고리즘 잠시 덮고 주특기 공부 바로 진입한다... 라지만 오늘 간만에 정리하는 블로깅 내용도 알고리즘:D
사실 얘를 먼저 공부했어야 옳을 것 같은데 힙을 먼저 공부하고(?) 뜬금없이 DFS와 BFS, 및 최소신장트리 등의 그래프 관련 알고리즘을 선행(?)한 다음에 알고리즘의 토대라고 볼 수 있는 정렬을 보게 되었다. 혹자는 나보고 트리 대신 그래프에 익숙한 게 신기하다 했는데 점점 내 공부도 신기함을 넘어 기묘해지는 과정을 몸소 체험하고 있다.
정렬은 단순 하나의 알고리즘을 일컫는 것이 아닌, 정말 다양한 알고리즘이 존재한다. 멀리 갈 것도 없이 우선순위 큐를 구현하는 데에 활용한 힙 구조 트리에서도 배열화시키면 그게 곧 힙 정렬이 된다. 그만큼 너무나도 중요해서 확실히 알고 넘어가야 할 내용.
1) 버블 정렬
 인접한 두 개의 원소를 비교해서 스왑(swap)하는 형식으로 이뤄지는 정렬이다. 위의 그림에서 (오름차순 기준으로) 인접한 정렬을 계속 자리바꾸기를 하면서 만약 앞선 인덱스의 값이 더 크면 뒤로 보내고 다음 인덱스로 향하는 식으로 최대값을 먼저 배치하게 된다.
인접한 두 개의 원소를 비교해서 스왑(swap)하는 형식으로 이뤄지는 정렬이다. 위의 그림에서 (오름차순 기준으로) 인접한 정렬을 계속 자리바꾸기를 하면서 만약 앞선 인덱스의 값이 더 크면 뒤로 보내고 다음 인덱스로 향하는 식으로 최대값을 먼저 배치하게 된다.
사실 엄청 선호되지는 않은 정렬일 것 같다(내 뇌피셜). 왜냐하면 최악의 경우를 상정했을 때, 모든 원소가 내림차순으로 정렬되어 있을 경우, 그걸 다시 오름차순으로 정렬하는 것은 배열의 모든 원소를 전부 훑게 되는 것이므로 하나하나 검색해서 확인하게 되는 경우와 다를 바가 없다.
물론, 뒷부분의 정렬이 끝나고, 바로 직전 인덱스까지만 버블 정렬이 이뤄지도록 별도의 조건을 걸면 조금의 효율을 추구할 수는 있지만... 그럴 바에 다른 거 쓴다(...) 전술한 조건이 걸린 경우에, 모든 원소가 처음부터 오름차순으로 정렬되어 있다면 한 번만 훑게 되는 경우가 그나마 최선이 될 것이다.
상기의 이유로, 시간복잡도 및 공간복잡도는 다음과 같다.
시간복잡도
- 최악 :
O(n^2)- 최선 : 조건이 없으면 동일, 조건이 있다면
O(n)공간복잡도
O(1): 별도의 메모리 할당 없이 해당 배열 내에서 작업이 이뤄지므로
2) 선택 정렬
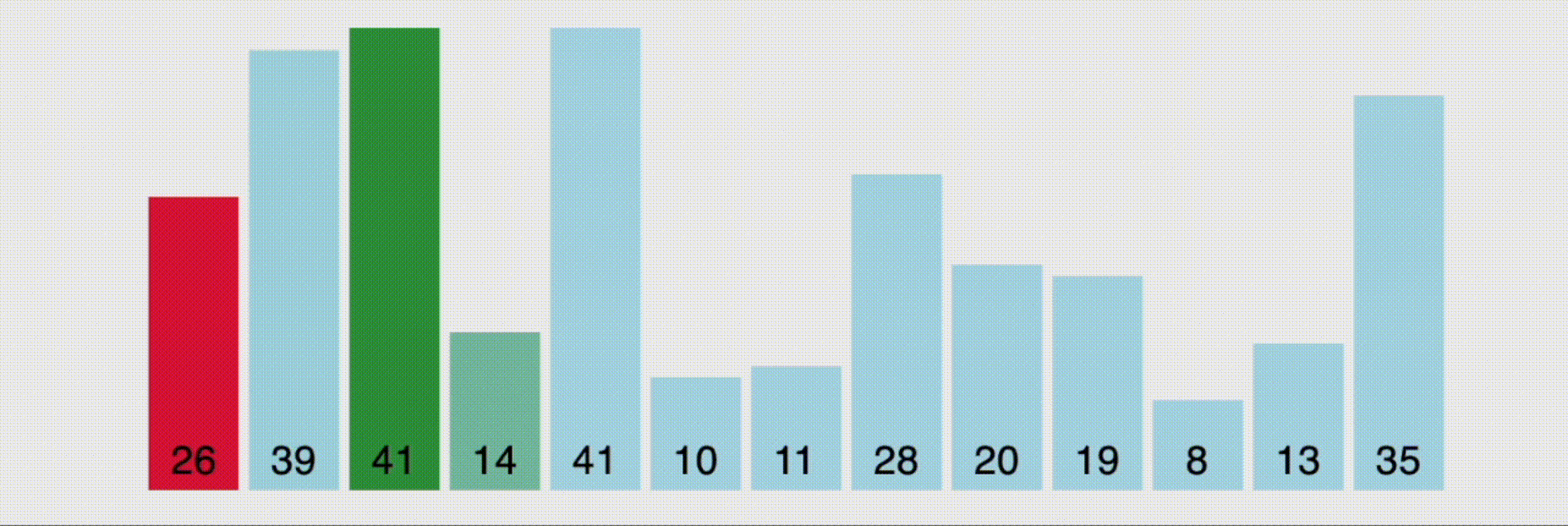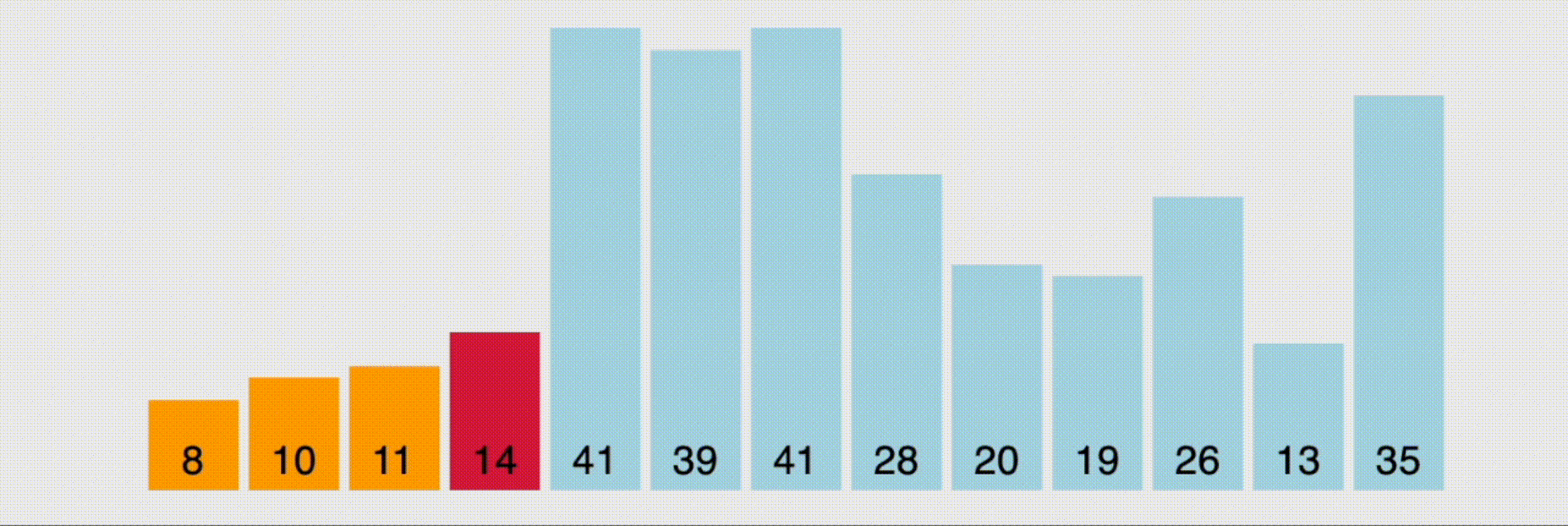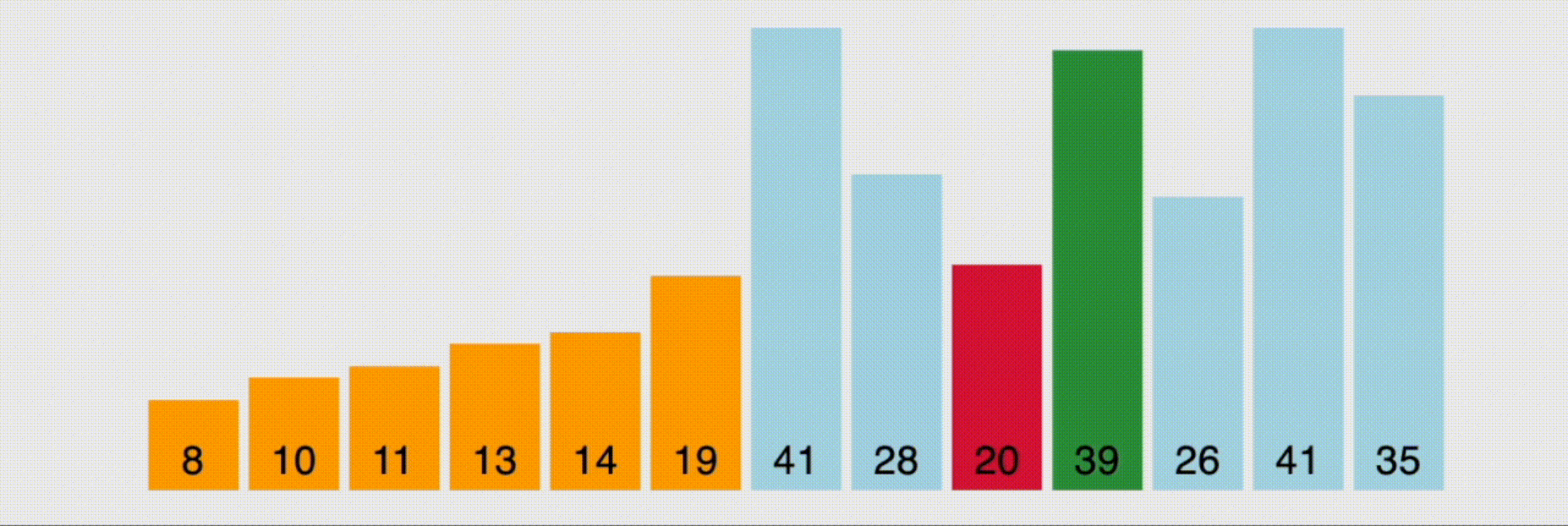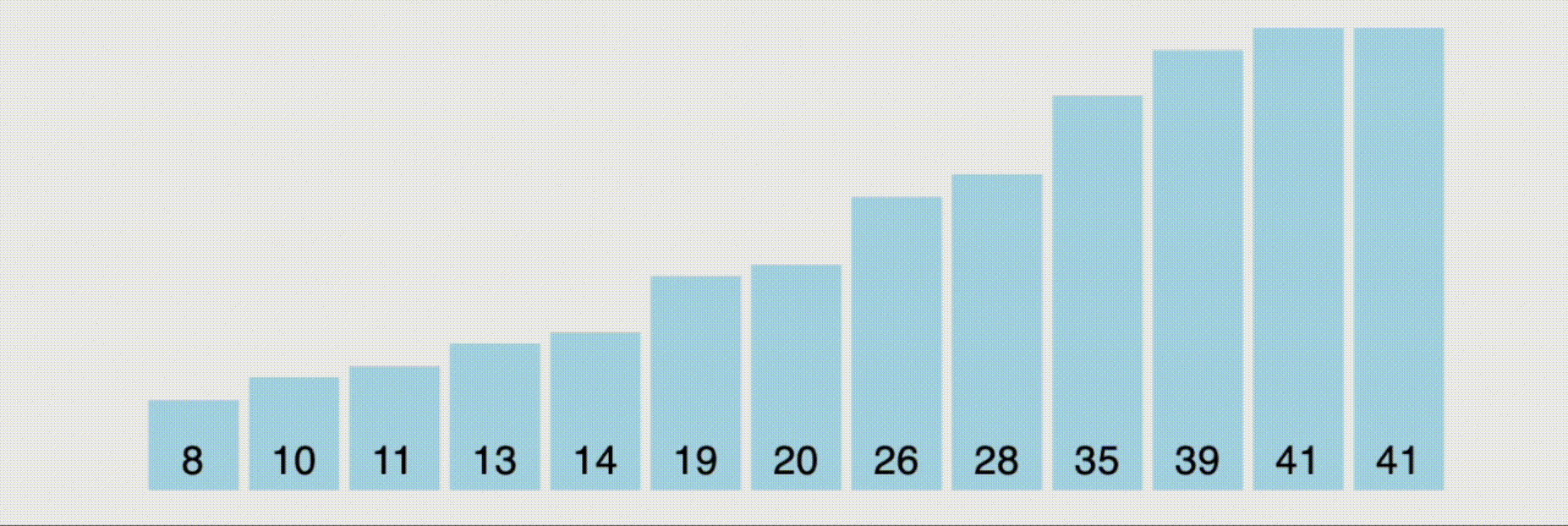 버블 정렬을 보고 선택 정렬을 봤을 때, 딱 느꼈다. 아, 얘는 버블 정렬 리버스구나... 왜 그렇게 생각했냐면 위의 그림처럼 가장 작은 데이터를 찾아서 가장 앞의 값과 스왑(swap)하는 과정을 거치며 정렬하기 때문이다. 즉, 인접하지 않았다는 것 뿐이고 최소값을 계속 업데이트해서 해당 인덱스를 업데이트 된 인덱스와 교체하는 작업일 뿐이지, 기본 흐름은 버블 정렬과 매우 유사했다.
버블 정렬을 보고 선택 정렬을 봤을 때, 딱 느꼈다. 아, 얘는 버블 정렬 리버스구나... 왜 그렇게 생각했냐면 위의 그림처럼 가장 작은 데이터를 찾아서 가장 앞의 값과 스왑(swap)하는 과정을 거치며 정렬하기 때문이다. 즉, 인접하지 않았다는 것 뿐이고 최소값을 계속 업데이트해서 해당 인덱스를 업데이트 된 인덱스와 교체하는 작업일 뿐이지, 기본 흐름은 버블 정렬과 매우 유사했다.
버블 정렬과 유사하다는 점에서 결국 쟤도 시간복잡도는 버블 정렬과 별반 다르지 않다. 모든 원소가 내림차순으로 정렬됐고 해당 원소들을 오름차순으로 정렬한다고 가정하면, 결국 쟤도 모든 원소를 훑으면서 지속적으로 최소값을 업데이트해줘야 하므로 역시 하나하나 검색해주는 것과 다를 바가 없어진다. 역시나 최선의 경우라면 조건을 걸어준 상태에서 미리 오름차순으로 정렬된 경우?
다만 버블 정렬과 비교했을 때, 성능적으로는 우수할 수 있다. 왜냐하면 버블 정렬은 인접한 원소끼리만 비교하지만, 선택 정렬은 인접 없이 인덱스와 인덱스 간의 비교이기 때문이다.
시간복잡도 및 공간복잡도는 다음과 같다.
시간복잡도
- 최악 :
O(n^2)- 최선 : 조건이 없으면 동일, 조건이 있으면
O(n)공간복잡도
O(1): 별도의 메모리 할당 없이 해당 배열 내에서 작업이 이뤄지므로
3) 삽입 정렬
 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입하는 방식의 알고리즘이다. 여기서 말하는 이미 정렬된이란, 위의 그림에서처럼 순차적으로 요소들을 앞의 인덱스 요소들과 본인의 크기를 비교하며 자신의 상대적인 위치를 찾기 위한 과정을 말한다.
모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입하는 방식의 알고리즘이다. 여기서 말하는 이미 정렬된이란, 위의 그림에서처럼 순차적으로 요소들을 앞의 인덱스 요소들과 본인의 크기를 비교하며 자신의 상대적인 위치를 찾기 위한 과정을 말한다.
얘 역시 결국 어떻게 보면 앞에 위치한 자신보다 큰 요소들과의 스왑 과정이 일어난다는 점에서 앞선 버블 정렬이나 선택 정렬과 유사해보이지만, 조건의 설정 없이 최선의 경우일 때와 최악의 경우일 때의 시간복잡도가 다르다. 왜냐하면 자신보다 작으면서 정렬된 요소들에 대해서는 더 이상 탐색하지 않아도 되기 때문이다.
버블 정렬과 선택 정렬보다는 우수한 성능을 지녔으며, 이미 정렬이 진행된 배열에 있어서는 시간이 그리 많이 소모되지 않는다는 장점 때문에 팀 솔트 등의 알고리즘의 부가적인 정렬 수단으로 활용되기도 한다. 또한 데이터의 개수가 많지 않은 경우일 때는 삽입 정렬이 훨씬 우수한 경우가 있다.
시간복잡도 및 공간복잡도는 다음과 같다.
시간복잡도
- 최악 :
O(n^2)- 최선 :
O(n)공간복잡도
O(1): 별도의 메모리 할당 없이 해당 배열 내에서 작업이 이뤄지므로
4) 병합 정렬
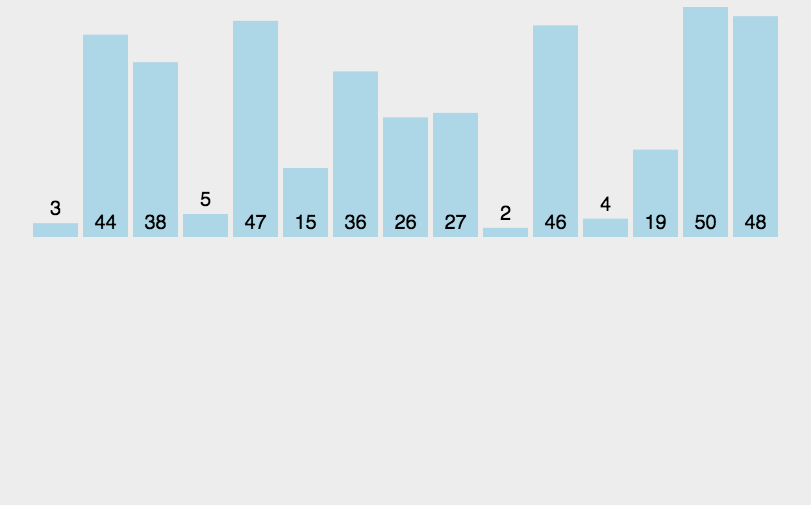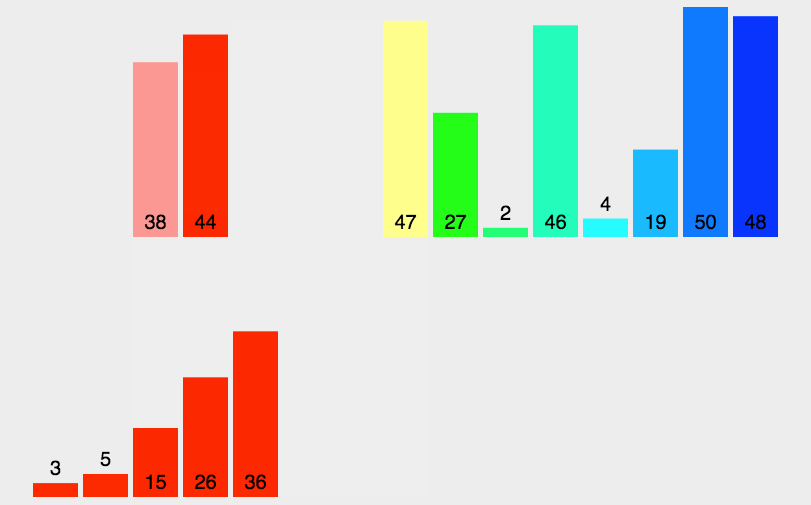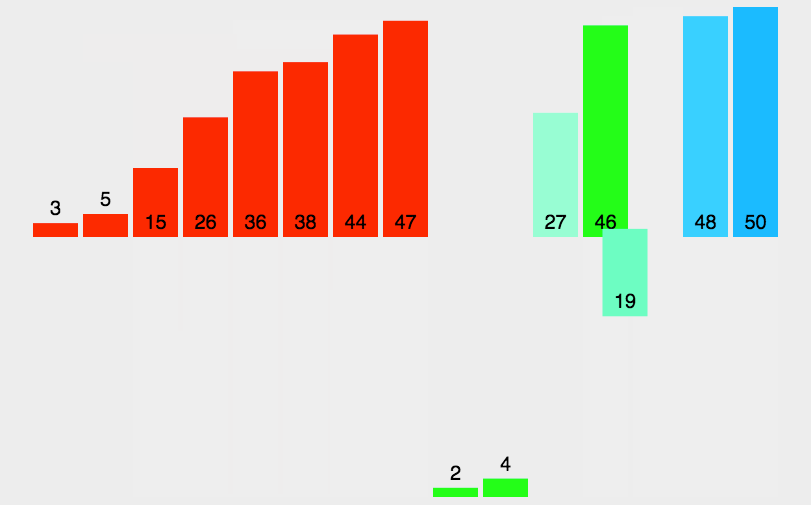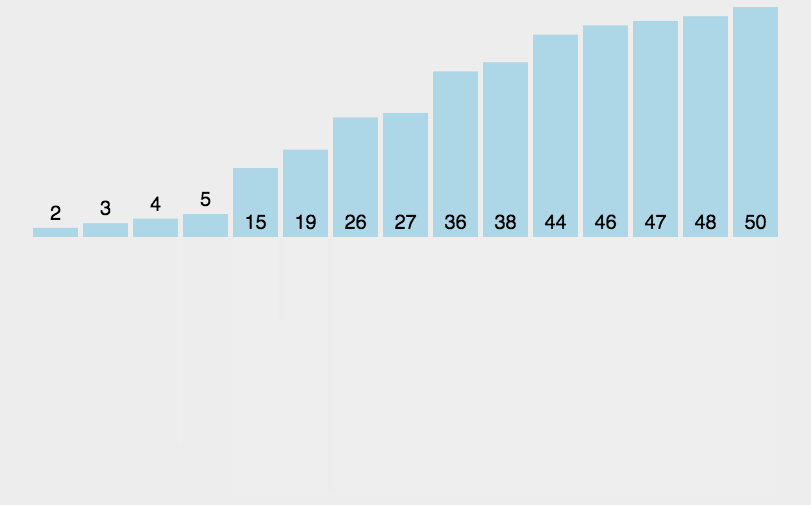 원본 배열을 절반씩 분할하면서 최대한 분할한 다음, 병합하는 과정에서 두 배열의 요소들의 서순을 비교 배치하면서 정렬하는 방식이다. 위의 그림에서 각각의 일치하는 색이 곧 병합 과정으로써 배치되는 과정이다.
원본 배열을 절반씩 분할하면서 최대한 분할한 다음, 병합하는 과정에서 두 배열의 요소들의 서순을 비교 배치하면서 정렬하는 방식이다. 위의 그림에서 각각의 일치하는 색이 곧 병합 과정으로써 배치되는 과정이다.
병합 정렬의 가장 큰 장점은 배열 자체를 절반으로 분리하면서 정렬을 수행하기 때문에 시간복잡도가 항상 일정하며, 앞선 세 개의 정렬보다 평균적으로 우수한 속도를 낼 수 있게 된다. 물론 장점만 존재하지는 않는데, 병합 과정에서의 정렬에 있어 임시로 배치를 위한 배열을 생성한 후에 원본 배열에 업데이트해주는 방식이 기본 골자여서, 추가적인 메모리 할당이 필요해진다.
물론 그것을 감안해도 앞선 정렬들에 비해 항상 빠른 속도를 내기 때문에 유용하게 활용되며 병합 정렬과 삽입 정렬을 합친 팀 솔트를 기반으로 한 파이썬의 sorted() 메소드가 예시가 될 수 있다.
시간복잡도 및 공간복잡도는 다음과 같다.
시간복잡도
- 최악 :
O(n logn)공간복잡도
O(n): 임시 배열 할당을 위한 별도의 메모리 소모가 필요
5) 기타 정렬(퀵, 힙)
아직 의사코드만 작성한 상태이고, 구현은 이뤄지지 않아서 추후 구현 완료 시 업데이트 예정
6) 알고리즘 구현
(1) 버블 정렬, 선택 정렬, 삽입 정렬
https://github.com/kimD0ngjun/algorithm_structure/blob/main/src/algorithm/sort/Sorts.java
(2) 병합 정렬
자바
https://github.com/kimD0ngjun/algorithm_structure/blob/main/src/algorithm/sort/MergeSort.java
파이썬
https://github.com/kimD0ngjun/algorithm_structure/blob/main/src/algorithm/sort/merge_sort.py
