9. 다익스트라 알고리즘
정렬, 탐색 등의 직관적인 이름인 알고리즘과 달리 얼마나 무시무시하면(?) 사람 이름이 들어갔을까... 걱정했던 알고리즘인 다익스트라. 덤으로 비공개글로 메모 작성 때 외에는 바빠서 엄두도 못 났던 블로깅
그래프 중에서 간선에 가중치가 존재하는 그래프와 관련해서는 프림 알고리즘으로 다뤄본 적이 있다. 다만 최소신장트리는 느낌이 전체를 아우르며 관통할 수 있는 최소 가중치 간선의 집합을 찾는다면, 다익스트라는 특정 정점을 기산점으로 삼아 다른 정점까지의 최단 경로를 탐색하게 된다.
처음에는 프림 알고리즘과 결합해서 생각하려고 했는데 역시 날먹은 업보로 돌려받는다. 꽤나 고생했다(...)
1) 최단 경로와 최소 가중치
사실 최소 가중치면 곧 최단 경로의 요소가 될 수 있는 거 아니냐고 생각하면서 정리했는데 맞는 말이긴 한데, 이걸 기반으로 프림 알고리즘이랑 유사하다고 생각한 내 멍충멍충한 사고를 탓해야 한다..(반성해라 나 자신)
원론적으로 프림과 다익스트라가 다를 수밖에 없는 이유는, 프림은 정점의 관점에서 바라보고, 다익스트라는 간선의 관점에서 바라보기 때문이다. 좀 뚱딴지 같은 소리지만(사실 그럴 수도 있다. 사견이 듬뿍 담긴 공부 기록이므로) 알고리즘을 직접 구현하면서 느낀 바였고 저 느낌이 곧 다익스트라를 이해하는 데에 큰 도움을 줬기 때문이다.
(1) 프림 알고리즘과의 차이점
프림과 다익스트라 둘 다 반복을 통해 탐색을 수행한다는 공통점이 있지만, 각 반복 분기에서의 행동 하나를 비교해보면 좋을 것 같다.
프림
반복 분기마다 탐색된 정점에게 인접한 간선들을 순회해서 최소 가중치를 계산한다.
다익스트라
반복 분기마다 탐색된 간선들을 순회해서 최소 가중치를 계산한다.
표현이 미묘하면서도 분명 다르다. 프림 알고리즘의 최소신장트리 형성 과정을 머릿속으로 생각해보자. 확장된 정점의 뭉치들에게 인접한 간선들을 전부 순회해서 그중 최소 가중치 간선을 뽑고, 그 간선과 인접된 정점을 뭉치에 포함시킨다. 그렇게 됨으로써 나머지 간선들은 더이상 고려 대상이 아니게 된다. 즉, 방문 처리를 위한 별도의 과정이 필요하단 뜻이다.
반대로, 다익스트라는 반복 분기마다 추출하는 것은 간선의 가중치 뿐이다. 물론 추출 과정에서 간선의 정보 역시 포함되지만, 그것은 순수하게 다음 간선의 정보들을 탐색해서 현재까지의 최소 거리를 힙 구조 등으로 선별하기 위한 추출용 보조 데이터에 불과할 뿐이지, 방문 처리가 필요하지 않다. 왜냐하면, 특정 정점을 기산점으로 두고 다른 정점들까지의 각각의 최단 경로 가중치를 탐색하는 과정에서 필요하다면 다른 최단 경로가 거쳐간 정점을 다시 거쳐야 할 필요성이 있기 때문이다.
(2) 최단 경로 및 가중치 탐색 과정
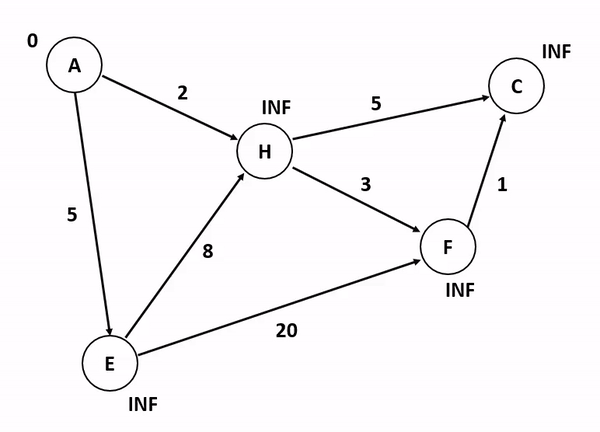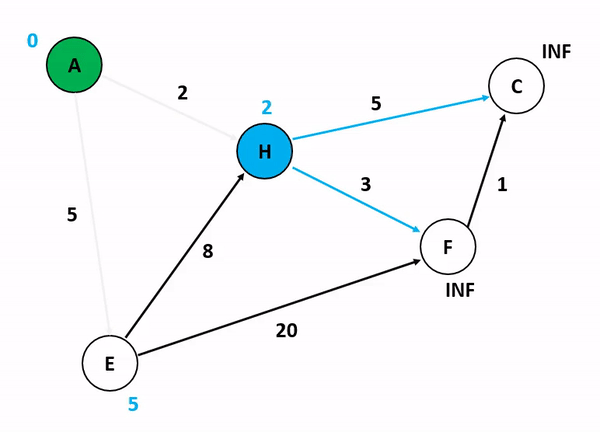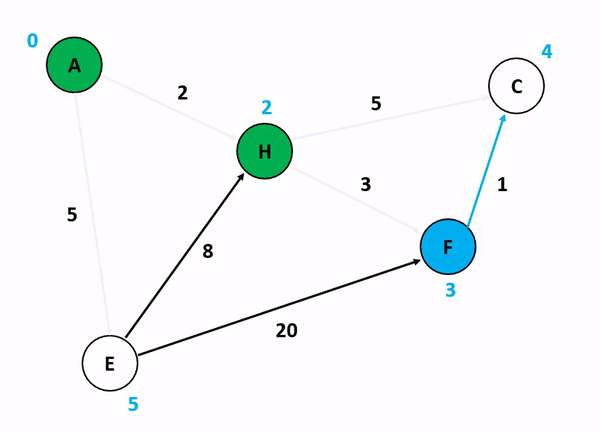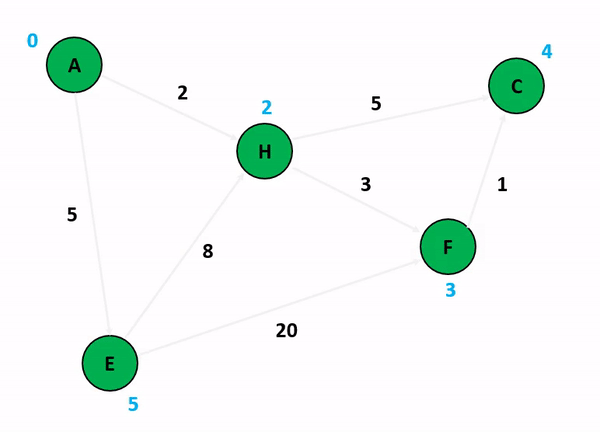
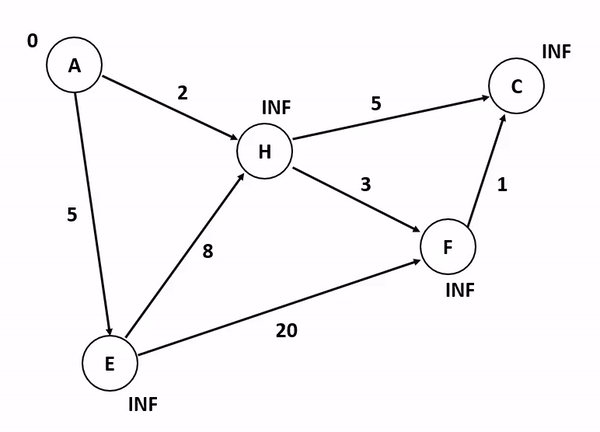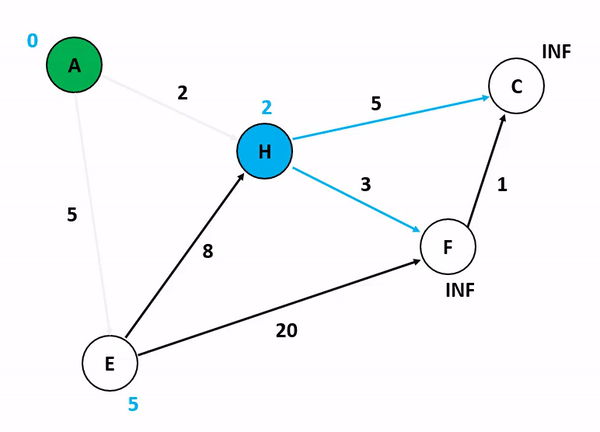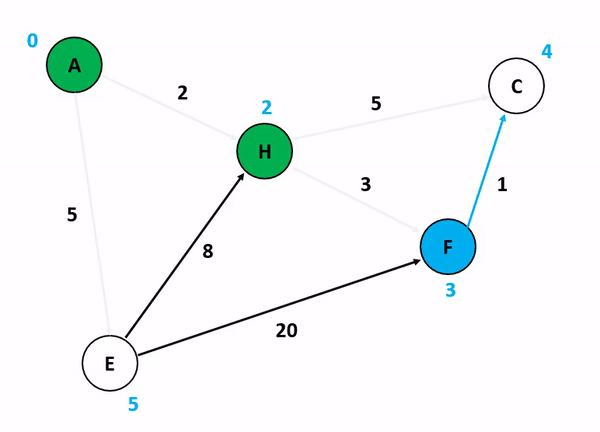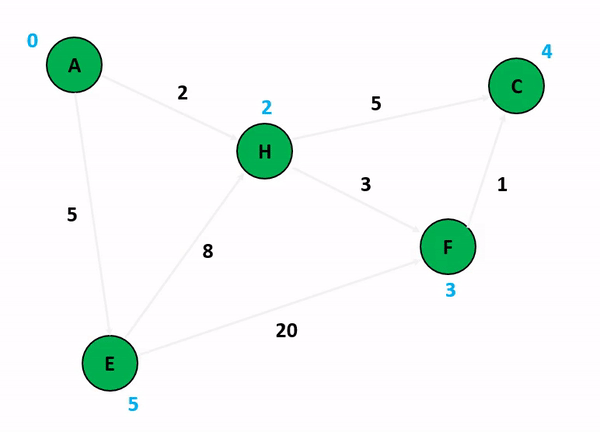
위의 그림은 다익스트라 알고리즘을 기반으로 정점 A에서 다른 정점들까지의 각 최단 경로 및 최소 가중치를 산정하는 과정이다. 저기서 A 정점에서 C 정점까지 가는 경우와 A 정점에서 F 정점까지 가는 경우를 생각해보자. 만약 여기서 정점의 방문 여부를 고려하게 된다면 A에서 C로 갈 수 있는 방법을 고려하는 것이 매우 복잡해진다. 앞서 말했듯이 다익스트라 알고리즘이 집중하는 것은 순수하게 인접 간선의 가중치를 더해서 특정 정점까지의 간선 가중치 합산 최소값을 업데이트하는 것이기 때문이다.
특이한 점은, 초기화 단계에서 도착 정점들까지의 최단 경로를 INF로 설정하는 것인데, 저것은 알고리즘 구현 언어 내부에서 고려할 수 있는 가장 최대값 혹은 값 비교가 무의미한 무한 상태로 초기화를 함으로써 반복 분기마다 지속적으로 얻어지는 최소값을 업데이트하기 위한 초기값인 셈이다.
유독 방문 처리와 관련해서 기록을 남기는 것은, 다익스트라의 구현 방법이 대표적으로 이중 리스트(혹은 배열)를 기반으로 한 순회 탐색과, 최소 힙 구조를 활용한 순회 탐색이 있기 때문이다. 이들 중, 이중 리스트 기반 구현 방식은 아까 내가 필요없다고 했던 방문 처리가 필요하다. 왜냐하면 최소 가중치 합산 산정 과정에서 만약 최단 경로 계산이 끝난 정점이 있어도 또 계산을 수행하며 무한루프에 빠지는 것을 방지하기 위해서다.내가 이래서 이중이란 단어를 싫어한다. 이중 리스트, 이중 배열, 이중 반복문, 이중사고, 이중인격, 이중중중중...
반대로 최소 힙 구조 활용 구현은 방문 처리가 필요 없다. 어차피 최소값을 추출하게 되고, 우선순위 큐가 비워질 때까지 반복하는데, 최소값으로 업데이트되지 못한 간선 가중치 합은 자연스럽게 배제(continue 등의 문법이나 if 조건문으로)될 것이기 때문이다.
2) 다익스트라 알고리즘 구현
다익스트라 알고리즘은 개념 이해 후에는 흐름이 빠르게 이해됐다. 하지만 이제 이걸 실전 문제풀이에서 능수능란하게 활용할 수 있냐는 다른 문제다. 내가 그래프에서 가장 어려워하는 유형이 사이클 판별 문제인데, 여기에 다익스트라 알고리즘 풀이 요구까지 겹친다? 나 죽어
정점의 개수가 V이고, 간선의 개수가 E인 그래프의 다익스트라 알고리즘 시간복잡도는 O(ElogV)로 계산된다.
구현 링크는 아래와 같으며, 구현 방식은 최소 힙 기반이다. 총 두 개의 메소드를 구현했는데, 하나는 기본적인 다익스트라 알고리즘 기반 그래프 최단 경로 탐색 메소드, 다른 하나는 다익스트라에서 확장해서 최단 경로를 출력하는 기능까지 덧붙여진 메소드다.
https://github.com/kimD0ngjun/algorithm_structure/blob/main/src/algorithm/pathFinder/dijkstra.py
