7. 최소신장트리
어제 내내 구현 유형에 갈리며 뇌를 말랑하다 못해 흐물하게 만드는 기이한 경험을 했다. 난해한 알고리즘보다는 구현 내용이 너무 많아서 문제의 단위화를 요구하는 유형이었는데... 이제 멀미가 난다.(우욱) 덕분에 어제 남겨야 했던 블로깅을 오늘 남기는 중...
트리는 그래프의 일종이다. 그래프에서 정점에 레벨 개념이 존재하고 자식이 두 부모를 가지지 않은 전제에서 루트 노드를 설정하면 그게 트리가 된다. 이 정의가 매우 중요하다. 오늘 기록을 남길 최소신장트리는 명칭은 트리지만, 활용은 그래프에서 활용되기 때문.
1) 최소신장트리 개념
(1) 정의
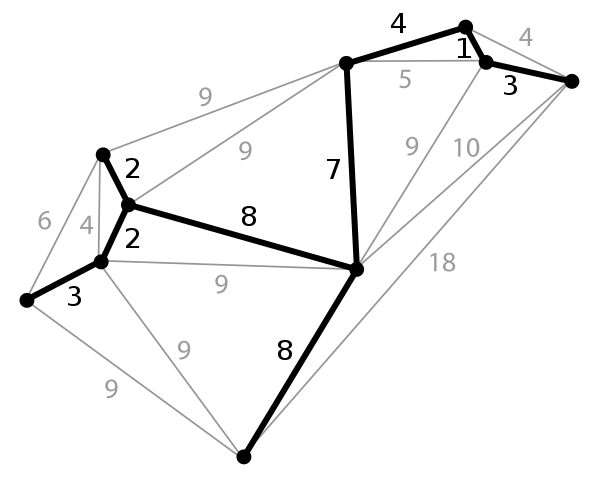
최소신장트리(Minimum Spanning Tree)는 최소 스패닝 트리라고도 하며, 간선에 가중치가 존재하는 그래프에서 최소 비용(가중치 할당량)만으로 모든 정점을 거치도록 하는 알고리즘이다. 즉 핵심은 연결된 간선들의 합이 최소여야 한다는 점이고, 총합이 최소이기 위해서는 탐색 분기에서 언제나 최소치의 간선을 선택해야 한다.
탐색 분기에서의 최선 선택이기 때문에 해당 알고리즘은 그리디에 속하며, 각 정점의 쌍을 모두 연결하는 간선들이 하나씩 존재하게 된다.
(2) 구현 방식
구현 방식은 다양하지만, 대표적으로 쓰이는 방식은 프림과 크루스칼 방식이 존재한다.
프림(Prim's Algorithm)
최소 힙을 바탕으로 구현된다. 동작 순서는 다음과 같다.
1. 시작 정점을 정한다.
2. 해당 정점과 연결된 간선(이웃하는 정점 객체)들을 탐색해서 최소 힙에 넣는다.
3. 최소 힙에서 최소치 간선을 추출해서 이웃 정점을 방문 처리한다.
4. 1번부터 3번까지의 과정을 반복해서 최소신장트리를 형성한다.
크루스칼(Kruskal’s Algorithm)
서로소 집합(분리 집합)을 바탕으로 구현된다. 동작 순서는 다음과 같다.
1. 가중치를 기준으로 간선 정보를 오름차순 정렬해서 최소치 간선을 추출한다.
3. 서로소 집합을 활용해서 현재까지의 간선들이 사이클을 형성하는지 확인한다.
4. 사이클을 형성하지 않는 간선을 추출하면 잇는다.
5. 1번부터 3번까지의 과정을 반복해서 최소신장트리를 형성한다.
정점의 개수가 n이고, 간선의 개수가 k라면 두 방식 전부 시간복잡도는 O(klogn)이 걸리게 된다. 간선의 개수가 증가할 수록 정렬 할당이 많아지기 때문에 간선이 적을수록 크루스칼이 유리하다. 반대로 간선의 개수가 적으면 최소 힙을 유지하는 것이 오히려 낭비일 수 있어서 간선이 많을수록 프림이 유리하다.
2) 프림 알고리즘 구현
크루스칼 알고리즘은 서로소 집합을 아직 구현하지 못해서 프림까지만 구현했다. 사실 프림을 구현하려면 최소 힙을 직접 커스터마이징해서 접목시키는 것이 옳지만 그렇게 되면 너무 효율성이 떨어지게 되므로 예전에 의사코드로 작성한 개념을 바탕으로 동작 원리를 이해하면서 python의 heapq 모듈을 기반으로 구현했다.
향후에 크루스칼 알고리즘도 구현해서 추가할 예정이지만, 그 전에 유니온 파인드 자료구조부터 이해해야 함...
프림 알고리즘 구현 전제조건과 링크는 아래와 같다.
- 그래프 정점은 정수형 데이터를 담는다.
- 간선 정보는 이웃 정점의 참조 객체와 가중치를 튜플로 관리한다.
- 그래프는 딕셔너리 구조를 바탕으로 정점 당 간선 정보를 담아 표현한다.
