힙에 관하여
이전 포스트에서 힙을 이용한 정렬인 힙 정렬에 대해 소개했다. 힙 정렬은 분명 훌륭한 알고리즘이지만 사실 나중에 소개할 퀵 정렬을 잘 구현하는 것이 일반적으로는 더 빠르다. 하지만 힙은 여러 방면으로 유용하게 사용할 수 있는데 이번 포스트에서는 힙을 가장 잘 응용하여 널리 쓰이고 있는 우선순위 큐를 소개해보려고 한다.
우선순위 큐
키라는 값을 가진 원소들을 다루기 위한 자료구조
보통의 큐는 FIFO를 구현한다. 따라서 우선순위에 상관없이 무조건 먼저 들어온 원소가 가장 먼저 나간다. 하지만 우선순위 큐에서는 우선순위에 따라 나가는 순서가 결정된다. 가장 나중에 들어온 원소이더라도 우선순위가 가장 높다면 가장 먼저 나가게 되는 것이다.
우선순위 큐의 종류
힙과 같이 우선순위 큐에도 최대 우선순위 큐와 최소 우선순위 큐로 나뉜다. 말 그대로 최대 우선순위 큐는 우선순위가 가장 높은 순서대로 아웃풋이 나가는 거고 최소 우선순위 큐는 우선순위가 가장 낮은 순서대로 나간다. 여기서는 최대 우선순위 큐를 중심으로 다뤄볼 것이다.
Ex)
1. 공유 컴퓨터 작업 순서 (최대 우선순위 큐)
일반적으로 공유 컴퓨터에서 작업 순서를 정하기 위해서는 그 작업의 우선순위에 따라 작업을 실행해야한다. 따라서 이 순서를 정하는데 최대 우선순위 큐를 사용한다면 중요도가 높은 순서대로 작업을 실행할 수 있다.
- 사건 반응형 시뮬레이터
한 사건의 시뮬레이션이 미래에 시뮬레이트되는 다른 사건에 영향을 줄 수 있으므로 시뮬레이션은 사건 발생 시간 순서대로 해야한다. 따라서 시뮬레이션 프로그램 최소 우선순위 큐를 사용하여 시뮬레이션을 진행할 수 있다.
기본 연산
1. Insert(S, x)
최대 우선순위 큐(S)에 원소 x를 새로 넣는다.
2. Maximum(S)
최대 우선순위 큐(S)에서 키값이 최대인 원소를 리턴한다.
3. Extract-Max(S)
최대 우선순위 큐(S)에서 키값이 최대인 원소를 제거한다.
4. Increase-Key(S, x, k)
원소 x의 키값을 k로 증가시킨다. 단 이때 k는 x의 원래 키값보다 작아지지는 않는다고 가정한다.
최소 우선순위 큐에서는 Insert를 제외한 모든 연산이 반대가 된다고 생각하면 된다.
기본 연산 구현
이제 실제로 위의 연산을 코드로 구현해보자. 가장 쉬운 것부터 시작하자면 Maximum이 가장 쉬울 것이다.
- Heap-Maximum
function HeapMaximum(A) {
return A[0]
}수행시간: O(1)
상수 시간안에 실행된다.
당연하지 이렇게 간단한데
작동원리:
- 루트 노드의 값을 반환한다.
그 다음으로 까다로운 연산은 가장 큰 값을 제거하는 것이다. 가장 큰 값을 제거하는 연산은 다음과 같이 구현할 수 있다.
- Heap-Extract-Max
function HeapExtractMax(A) {
if A.heapSize < 1 {
throw new Error("heap underflow");
};
max = A[0];
A[0] = A[A.heapSize];
A.heapSize = A.heapSize - 1;
MaxHeapify(A, 0)
return max
}수행시간: O(lg n)
MaxHeapify함수는 O(lg n)시간이 걸리고 나머지 코드들은 상수 시간만을 필요로 하기 때문에 Heap-Extract-Max함수의 수행시간은 O(lg n)이 된다.
작동원리:
1. 힙의 루트 노드의 값을 구한다.
2. 루트 노드의 위치에 가장 뒤에 있는 노드의 값을 끼워 넣는다.
3. 최대 힙 특성을 만족하기 위해 MaxHeapify함수를 실행한다.
- Heap-Increase-Key
function HeapIncreaseKey(A, i, key) {
A[i] = key
while(i > 1 && A[Parent(i)] < A[i]) {
A[i] = A[Parent(i)
A[Parent(i)] = A[i]
i = Parent(i)
}
}수행시간: O(lg n)
수행시간이 O(lg n)인 이유는 주어진 인덱스로부터 루트까지의 길이가 O(lg n)이기 때문이다.
작동원리:
1. 주어진 인덱스의 노드의 키를 입력받은 값으로 올린다.
2. 자신의 위치부터 루트 노드의 위치까지 올라가며 최대 힙 특성을 만족하는지 확인한다.
3. 만약 자신의 키가 부모의 키보다 크다면 while문을 반복하고 작다면 최대 힙 특성을 만족한다는 의미이기에 중단한다.
- Max-Heap-Insert
function MaxHeapInsert(A, key){
A.heapSize = A.heapSize + 1;
A[A.heapSize] = -∞
HeapIncreaseKey(A, A.heapSize, key)
}수행시간: O(lg n)
HeapIncreaseKey의 수행시간이 O(lg n)이기 때문 (나머지는 모두 상수 시간이 걸린다.)
작동원리:
1. 노드를 추가할 예정이기 때문에 heapSize를 1 늘린다.
2. 새로 들어오는 키 값은 원래 있던 값보다 작을 수 없기 때문에 새로 들어오는 키 값이 절대 작을 수 없도록 새로 들어올 노드의 키 값을 -∞로 설정한다.
3. HeapIncreaseKey를 실행시켜 새로 들어온 노드의 키값을 바꾸고 제자리로 옮긴다.
결론
위의 4가지 함수를 보다보면 1가지를 제외하고는 모두 같은 공통점이 보인다. 수행시간이 모두 O(lg n)이라는 것이다. 사실 우선순위 큐는 굳이 힙을 사용하지 않더라도 만들 수 있다. 하지만 다른 자료구조를 사용한 우선순위 큐의 치명적인 단점은 Insert에 소요되는 시간이 O(n)으로 너무 많다는 것이다.
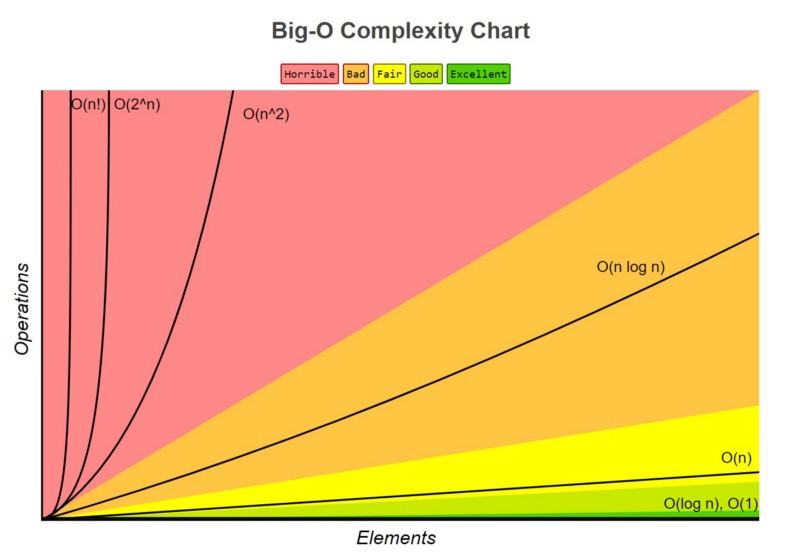
위에 사진을 보면 알 수 있듯이 O(lg n)과 O(n)사이에는 엄청난 차이가 있다. 따라서 많은 사람들이 우선순위 큐를 힙으로 구현한다.
사실 이전에 프로그래머스에서 연습 문제를 풀던 중 우선순위 큐를 사용하는 문제가 있었는데 그땐 이 멋진 우선순위 큐를 알지 못해서 그 문제를 풀지 못했다. 다음에 시간이 된다면 우선순위 큐를 사용하여 그 문제를 해결해 봐야겠다.

