퀵 정렬은 찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘이다. 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 퀵 정렬은 n개의 데이터를 정렬할 때, 최악의 경우에는 O(n²)번의 비교를 수행하고, 평균적으로 O(n log n)번의 비교를 수행한다. - 위키백과 -

1. 퀵 정렬?

퀵 정렬은 n개의 원소를 가진 배열을 최악의 경우에 O(n²)시간에 정렬하는 알고리즘이다. 이렇게 최악의 경우로만 봤을땐 퀵 정렬은 느리지만 평균 수행시간이 O(n lg n)으로 굉장히 효율적이고 O(n lg n)에 숨겨진 상수 인자도 굉장히 작다.

퀵 정렬은 병합 정렬과 마찬가지로 분할정복에 기반을 두고 있다. 따라서 퀵 정렬의 동작은 다음과 같이 설명할 수 있다.

분할: 배열 A[p..r]을 두 개의 부분 배열 A[p..q-1]과 A[q + 1..r]로 분할한다. A[p..q-1]에는 q보다 작거나 같은 원소를 A[q + 1..r]에는 q보다 크거나 같은 원소를 넣는다. 이 분할 과정을 위해 인덱스 q를 계산한다

정복: 퀵 정렬을 재귀 호출해서 A[p..q-1]과 A[q + 1..r] 두 부분 배열을 정렬한다.

결합: 부분 배열이 이미 정렬된 상태이기 때문에 이 작업은 필요가 없다.

자 이렇게만 보면 이게 무슨 복잡한 말인가 싶을 수 있다. 쉽게 설명하자면

1. 배열의 마지막 원소를 q로 정한다
2. 배열의 0번째 원소부터 q - 1번째 원소까지 q와 비교하여 q보다 작거나 같다면 왼쪽으로 크다면 오른쪽으로 나눈다.
3. 위의 과정을 재귀호출하여 더 이상 나눌 수 없을때까지 반복한다.

그림으로 보면 다음과 같다.

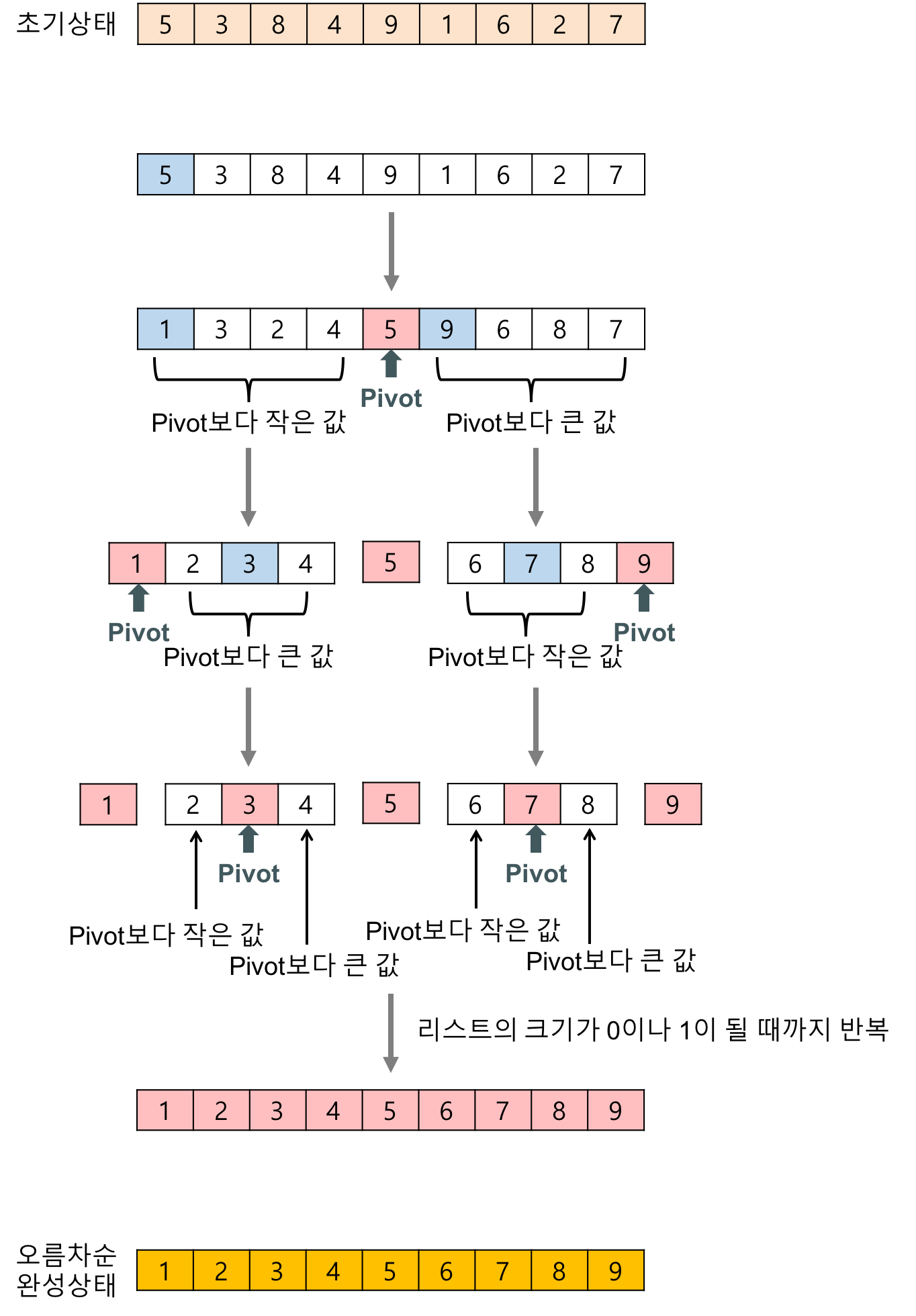
다음은 퀵 정렬을 구현한 코드이다.

def Quicksort(A, p, r):
 if p < r:
  q = Partition(A, p, r)
  Quicksort(A, p, q - 1)
  Quicksort(A, q + 1, r)

1. 배열이 충분히 큰지 확인한다.
2. 인덱스 q를 구하고 q의 크기에 따라 작은 값은 왼쪽으로 큰 값은 오른쪽으로 정렬한다.
3. Quicksort를 재귀 호출한다.

다음은 Partition의 코드이다

x = A[r]
i = p - 1
for j = p to r - 1:
 if A[j] <= x:
  i = i + 1
  A[i]와 A[j] 교환
A[i + 1]와 A[r] 교환
return i + 1

결론

퀵 정렬은 분할정복 방식을 이용한 정렬 알고리즘이다. 최악의 경우 O(n²)의 시간이 걸리지만 평균적으로 O(n lg n)시간에 끝나는 굉장히 효율적인 알고리즘이다. 심지어 나중에 설명하겠지만 대부분의 경우 굉장히 효율적으로 O(n lg n)시간에 끝나는 모습을 볼 수 있다. 다음 포스트에서는 퀵 정렬의 성능에 대해서 알아보자