Big-O-Notation (점근 표기법)

Big-O-Notation

• 알고리즘의 속도를 표현하는 방법이다

알고리즘의 속도는 초와 같은 단위로 나타낼 수 없다. 왜냐하면 같은 코드를 실행하더라도 코드를 돌리는 하드웨어에 따라 속도 차이가 천차만별이기 때문이다. 따라서 작업을 수행하는데 걸리는 Step에 따라 속도를 계산한다.

Ex) 수행하는데 5개의 스텝이 필요한 알고리즘이 10개의 스텝이 필요한 알고리즘보다 효율적임

• 코드의 실제 러닝 타임을 표시하는 것이 아니며, 인풋 데이터 증가율에 따른 알고리즘의 성능을 예측하기 위해 사용한다.

실제 러닝 타임을 표시하지 않는 이유는 만약 알고리즘이 4n + 9시간이 걸린다고 가정했을때 n이 10억이라면 이 알고리즘이 돌아가는데는 40억 + 9시간이 걸린다고 말하는 사람은 아무도 없을 것이다.

따라서 Big-O-Notation은 다음과 같은 규칙을 사용한다.

1. 가장 높은 차수만 남긴다.

O(n² + n) -> O(n²)   

차수가 없는 n은 알고리즘의 실행시간에 거의 영향을 미치지 못하기 때문

2. 계수 및 상수는 과감하게 버린다.

O(2n + 3) -> O(n)
O(3N) ➡ O(N)
O(N² +2) ➡ O(N²)

마찬가지로 계수 및 상수는 알고리즘의 실행시간에 영향을 끼치지 못한다.

예시

1. 상수 시간

function getFirstItem(arr) {
  return arr[0];
}

위 코드는 배열을 인풋으로 받아 첫번째 값을 리턴하고 있다. 이 경우 배열이 얼마나 큰지는 상관없이 무조건 첫번째 값을 리턴하기때문에 배열의 크기와 상관없이 시간이 결정된다.

따라서 위 함수의 시간복잡도는 constant time (상수 시간)이라고 할 수 있다.

그렇다면 만약에 위 코드를 다음과 같이 바꾸면 시간복잡도가 O(2)가 될 수 있을까?

function getFirstItem(arr) {
  console.log(arr[0]);
  console.log(arr[0]);
}

정답은 No!이다. 위에서 언급했듯이 Big-O에서는 코드에 디테일한 부분에는 별로 관심이 없다. 따라서 실행시간이 입풋 데이터의 영향을 받지 않는다면 모두 O(1)이라고 표시한다.

위와 같이 상수 시간에 실행되는 코드들은 항상 선호되지만 현실적으로 만들기 어렵다는 문제가 있다.

2. 선형 시간

def printAll(arr):
 for n in arr:
  print(n)

위 코드는 배열을 입력받아 배열의 각 아이템을 모두 출력한다. 배열의 크기가 10이라면 10번 출력하고 100이라면 100번 출력한다. 즉 이와 같은 시간 복잡도를 Big-O로 표기한다면 다음과 같다.

위와 같은 알고리즘들은 모두 입력의 크기와 속도가 비례한다.

3. 2차 시간

• 중첩 반복이 있을 경우 발생

def print_twice(arr):
 for n in arr:
  for x in arr:
   print(x, n)

위 코드는 배열의 각 아이템에 대해 루프를 반복하여 실행한다. 따라서 시간복잡도는 n^2가 되고 이 말은 10개의 아이템에 대하여 100개의 스텝이 필요하다는 말이다.

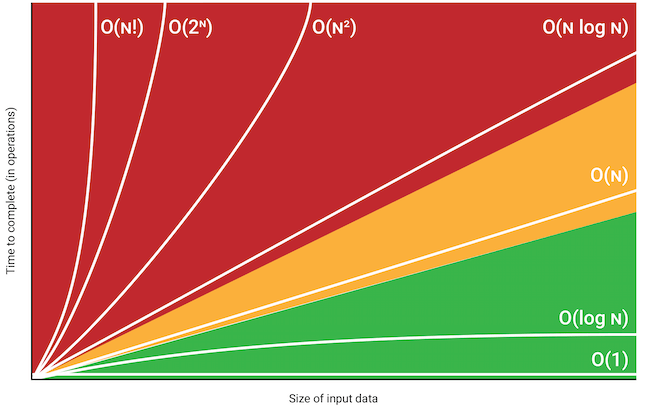
입력의 크기가 커질수록 시간이 기하급수적으로 증가하기에 별로 선호되지 않는 알고리즘이다.

4. 로그 시간
   먼저 로그에 대해 알아보자. 로그는 지수의 정 반대이다. 따라서 밑이 2인 로그에 32를 넣는다면 2^5가 32이기에 5가 결과로 나오게 된다. 이처럼 로그를 사용하면 엄청 입력에 비해 훨씬 작은 값이 나오게 되는데 그 결과 다음과 같은 그래프가 나오게 된다.

위 그래프를 보면 로그 시간은 선형 시간에 매우 근접해 있다는 것을 알 수 있다. 따라서 상수 시간 다음으로 가장 빠른 알고리즘에 속한다.