시작

오늘부터 Introduction to Algorithms에 대한 TIL을 진행하려고 한다.

왜 정렬 알고리즘인가?

수많은 컴퓨터 공학자가 정렬을 알고리즘 연구에서 가장 기본적인 문제로 여기고 있다고 저자는 말한다. 여기에는 몇가지 이유가 있는데

1. 정보를 정렬하는 것 자체가 필요한 응용 분야가 있다.
   Ex) 은행에서는 고객 청구서를 준비하기 위해 수표를 수표 번호순으로 정렬해야 한다.

2. 많은 알고리즘이 자주 정렬을 사용한다.
   Ex) 층을 이루는 물체를 그리는 프로그램은 밑바닥부터 꼭대기까지 순서대로 그릴 수 있도록 상하관계에 따라서 정렬해야한다.

3. 정렬 알고리즘은 종류가 다양하고 많은 기술이 적용된다.

힙

힙 자료구조는 완전 이진 트리로 볼 수 있는 배열 객체이다.

완전 이진 트리가 뭐지...?

완전 이진 트리: 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조

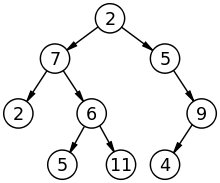
이 트리에서의 한 노드는 곧 배열에서 한 원소를 의미한다.

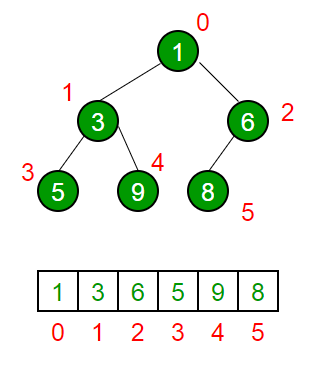
위 그림에서 볼 수 있듯이 트리는 마지막 층을 제외하고는 모두 가득 차 있고, 마지막 층은 왼쪽에서부터 차례대로 채운다.

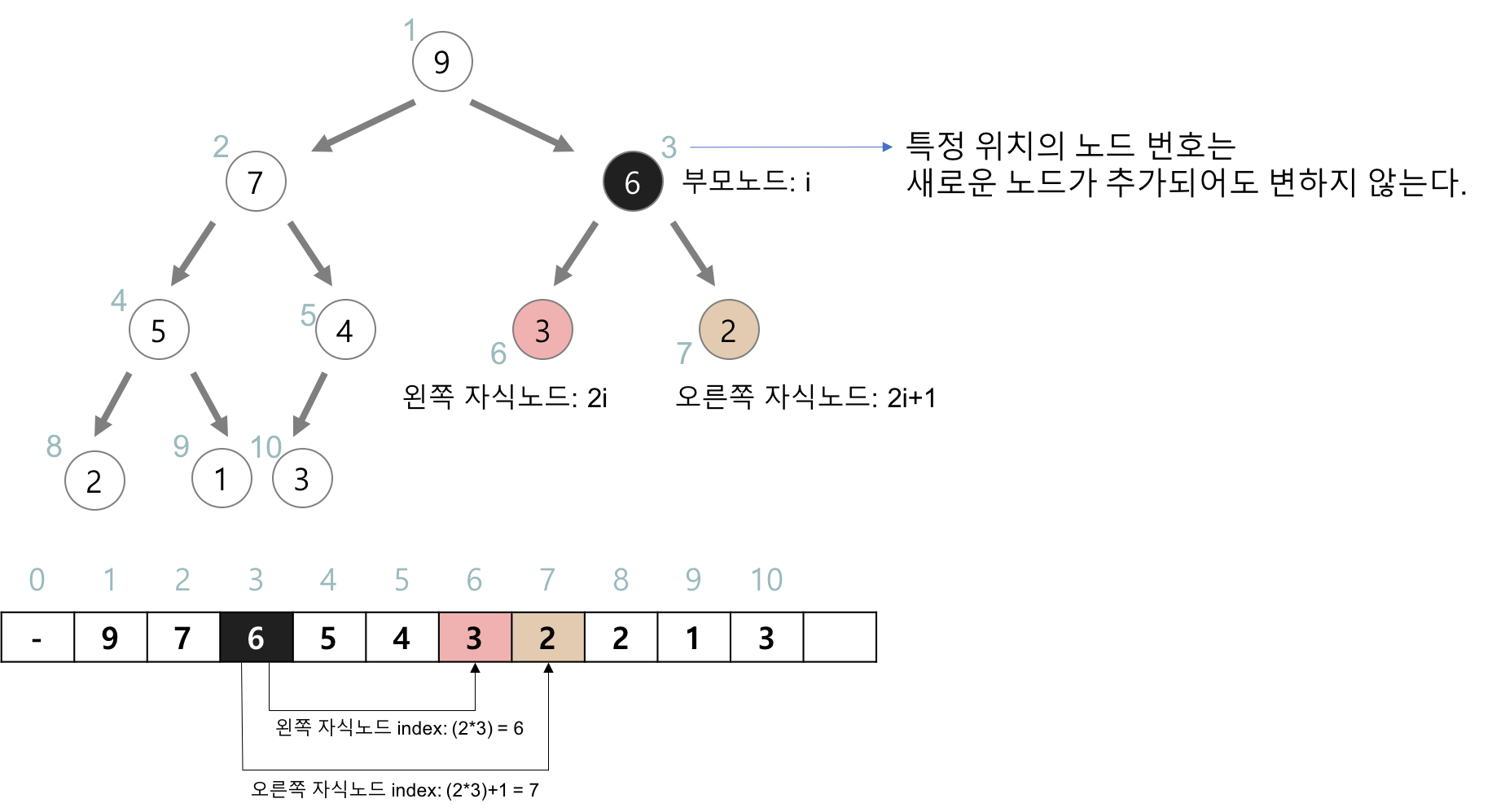
만약 노드의 인덱스가 주어진다면 그 노드의 부모, 왼쪽 자식, 오른쪽 자식은 다음의 식으로 간단히 구할 수 있다. (엄청 신기하다.)

부모 = i/2
왼쪽 자식 = 2i
오른쪽 자식 = 2i + 1

힙의 종류

1) 최대 힙

책에서는 최대 힙에 특성에 대해 다음과 같은 식으로 표현하고 있다.

A[Parent(i)] >= A[i]

당최 무슨 말인지 이해하기 힘들지만 쉽게 말하자면 부모 노드는 자식 노드보다 작을 수 없다는 것이다.

2) 최소 힙

이 또한 책에서는 A[Parent(i)] <= A[i] 라는 직관적으로 이해하기 어려운 식을 사용하여 설명하는데 말 그대로 최대 힙의 반대인만큼 가장 위에 있는 노드가 가장 작은 값이 된다는 것이다.

힙의 높이

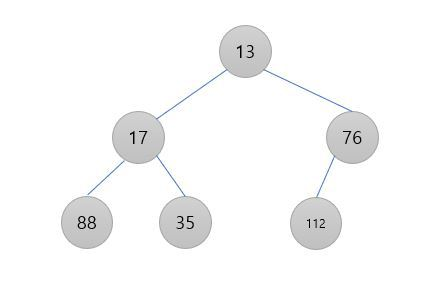
힙을 트리로 보는 관점에서 노드의 높이를 그 노드에서 리프에 이르는 하향 경로 중 가장 긴 것의 간선 수로 정의한다. 그리고 힙의 높이는 루트의 높이로 한다.

리프: 자식이 없는 노드 (가장 밑바닥에 있는 노드들)

정말 무슨 말인지 이해하기 어렵지만 사진과 함께 보면 이해하기 쉽다.

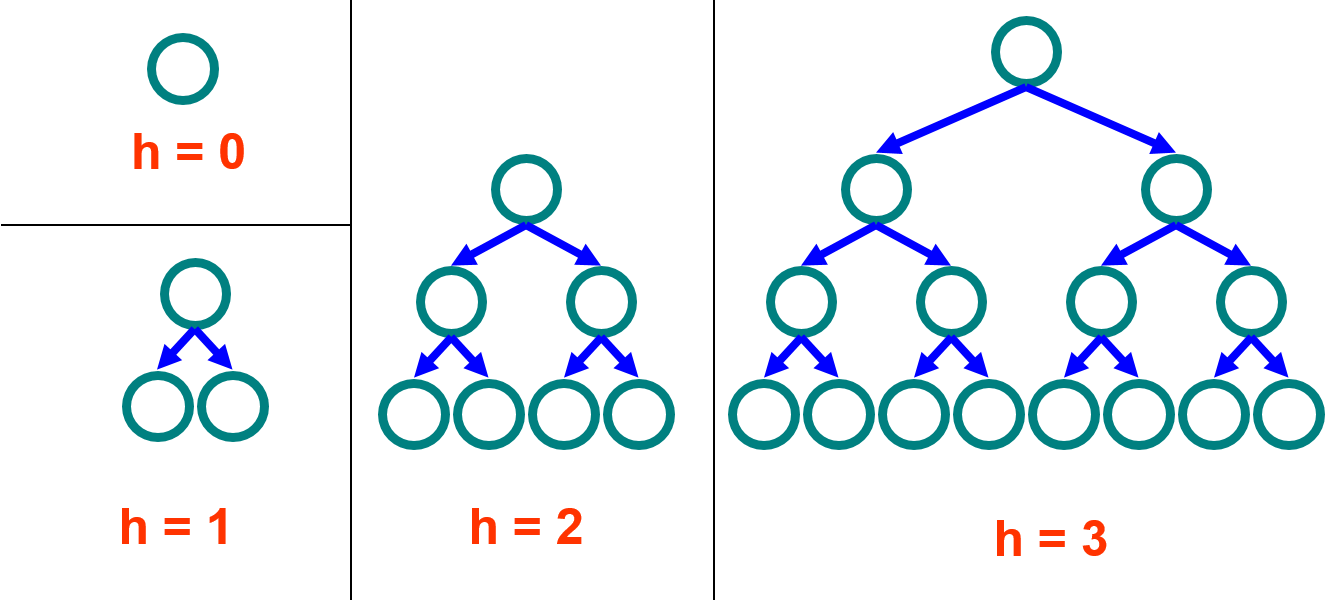
그냥 우리가 트리 한층 한층 세는 것처럼 세면 높이를 구할 수 있다. 그리고 힙의 높이는 가장 위에 있는 노드의 높이로 한다.

기본 연산

힙에 대한 기본 연산의 수행시간은 오래 걸려도 힙의 높이에 비례하는 정도이기 때문에 O(lg n) 이다.

1. Max-Heapify

• 최대 힙 특성을 유지하는데 핵심 역할을 한다.
• O(lg n) 시간에 실행된다.

2. Build-Max-Heap

• 정렬되지 않은 배열로부터 최대 힙을 만든다.
• 선형 시간에 실행된다.

3. Heapsort

• 배열을 내부 정렬한다.
• O(n lg n) 시간에 실행된다.

힙 특성 유지하기

최대 힙 특성을 유지하기 위해선 Max-Heapify를 사용한다. Max-Heapify는 입력으로 배열 A와 인덱스 i를 받는다.

function Max_Heapify(A, i) {
  let largest;
  const l = Left(i); // i의 왼쪽 자식
  const r = Right(i); // r의 오른쪽 자식

  if l <= A.heap-size && A[l] > A[i] { // l이 트리 안에 있고 l이 i보다 더 크다면
    largest = l;
  } else {
    largest = i;
  }

  if r <= A.heap-size && A[r] > A[largest] // r이 트리 안에 있고 r이 위에서 가장 컸던 값보다 더 크다면 {
      largest = r;
  }

  if largest != i { // i가 가장 큰 값이 아니라면 i와 가장 큰 값의 위치를 바꾸고 Max_Heapify를 다시 호출한다
    A[largest] = A[i]; 
    A[i] = A[largest] ;
    Max_Heapify(A, largest);
  }
}

사진으로 보면 다음과 같다.

각 단계에서 i, 왼쪽 자식, 오른쪽 자식 중 가장 큰 값이 정해지고 그 값의 인덱스를 largest에 저장한다. i가 최대값이라면 최대 힙 특성을 만족하므로 함수를 종료하지만 그렇지 않다면 i와 largest를 교환하여 노드 i와 그 자식이 최대 힙 특성을 만족하도록 한다. 그러나 이제 largest 위치의 노드는 원래의 A[i]값을 가지므로 largest를 루트로 하는 서브 트리가 최대 힙 특성과 맞지 않을 수 있다. 따라서 Max-Heapify는 그 서브 트리로 재귀 호출되어야 한다.

힙 만들기

정렬되지 않은 배열을 최대 힙으로 바꾸기 위해서는 Max-Heapify를 바닥에서부터 위로 올라가는 식으로 이용하여아 한다. 부분 배열 A[([n/2] + 1)..n]의 원소는 모두 트리의 리프다. 따라서 다음과 같은 코드를 만들 수 있다.

Build_Max_Heap(A)
A.heap_size = A.length
for i = [A.length/2] downto 1
	Max_Heapify(A, i)

책에서는 이 함수가 정확하게 동작함을 증명하기 위해 루프 불변성을 이용한다.

루프 불변성:

• 알고리즘이 타당하다는 사실을 증명하기 위해 사용된다
• 세 가지 특성을 만족해야 한다

1. 초기조건: 루프가 첫 번째 반복을 시작하기 전에 루프 불변성이 참이어야 한다.
2. 유지조건: 루프의 반복이 시작되기 전에 루프 불변성이 참이었다면 다음 반복이 시작되기 전까지도 계속 참이어야 한다.
3. 종료조건: 루프가 종료될 때 그 불변식이 알고리즘의 타당성을 보이는 데 도움이 될 유용한 특성을 가져야 한다.

Ex) 삽입정렬 알고리즘

1. 초기조건: 정렬 시작 전 배열[:1] 이 정렬되어 있어야 한다.
2. 유지조건: 매 반복시마다 배열[:index]가 정렬되어있어야 한다
3. 종료조건: 배열이 정렬되어있어야 한다

위의 Build-Max-Heap은 다음과 같은 루프 불변성을 이용한다.

2-3행에 있는 for 루프에서 반복을 시작할 때마다 노드 i+1, i+2, ...n은 모두 최대 힙의 루트가 된다.

1. 초기조건: 첫 번째 반복 전에 i = [n/2]이다. 각 노드 [n/2] + 1, [n/2] + 2,...n은 리프이므로 이들은 모두 최대 힙의 루트가 된다.

2. 유지조건: 각 반복에서 루프 불변성이 유지되는지를 보기 위해 노드 i의 인덱스보다 자식들의 인덱스가 크다는 점을 기억하자. 루프 불변성에 따라 자식들은 모두 최대 힙의 루트가 된다. 이는 노드 i를 최대 힙의 루트로 만들기 위해 Max-Heapify(A, i)를 호출할 때 필요한 조건이다. 게다가 Max-Heapify 호출은 노드 i+1, i+2, ...n이 모두 최대 힙의 루트라는 특성을 깨뜨리지 않는다. for 루프에서 i를 줄임으로써 다음 반복에서도 루프 불변성을 유지한다.

3. 종료조건: 종료할 때 i = 0이다. 루프 불변성에 따르면 노드 1,2,...n은 각각 최대 힙의 루트다. 특히, 노드 1이 최대 힙의 루트가 된다.

위에 어려운 말들을 아래 사진이 친절하게 설명하고 있다.

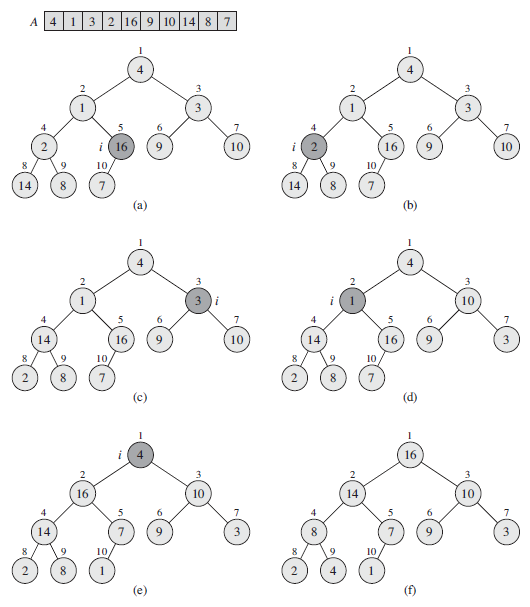
힙 정렬하기

드디어 제목인 힙 정렬이 등장했다. 하지만 조금만 생각해본다면 최대 힙으로 배열을 정렬하는 것이 얼마나 쉬운 일인지 깨닫게 될 것이다. (힌트: 최대 힙의 루트 노드는 배열에서 가장 큰 값이다.)

Heapsort(A){
  Build_Max_Heap(A); // 배열을 최대 힙으로 만들기
  for (i = A.length; i > 1; i--) {
    A[1] = A[i];
    A[i] = A[1];
    A.heap_size = A.heap_size - 1;
    Max_Heapify(A, 1)
  }
}

Build_Max_Heap이 O(n) 시간 걸리고 Max_Heapify를 n-1번 실행하는 것이 각각 O(lg n) 시간이 걸리므로 Heapsort의 수행시간은 O(n lg n)이다.

위 코드를 설명하자면 먼저 배열을 최대 힙으로 만든다. 그 후 배열의 가장 뒤에 값과 가장 앞에 값을 바꿔치긴한다. 그 후 루트 노드가 최대 힙 특성을 만족하지 못할 수 있기 때문에 Max_Heapify를 호출해서 최대 힙 특성을 유지해 준다. 그 후 위의 과정을 반복하면 값이 큰 순서대로 배열의 뒤쪽으로 오게 되고 그 결과, 정렬된 배열을 얻을 수 있다.

결론

오늘은 항상 궁금했던 힙이라는 자료구조와 그 특성 또한 이 구조를 통해 어떻게 배열을 정렬할 수 있는지까지 알아봤다. 대학 교재라는 점 때문에 여러가지 증명이 많고 복잡한 편이지만 그래도 하나 하나 천천히 하다보니 생각보다 엄청 어렵지는 않은 것 같다. (물론 루프 불변성과 시간 복잡도는 아직도 어렵다...) 다음 글은 우선순위 큐에 대해서 알아보자.