이번 시간에는 VAE(Variational Autoencoders)에 대해서 알아보겠습니다.
자세한 설명에 들어가기 앞서 VAE는 구조상 AE와 똑같지만 목적이 다릅니다.
AE는 manifold learning이 목적입니다. 즉 인코더에 포커스가 맞춰져 있습니다.
VAE는 Generative model입니다. 즉 데이터를 생성하기 위한 디코더에 포커스가 맞춰져 있는데 공교곱게도 AE와 구조가 같아졌을뿐 목적이 전혀 다르다는점을 알아야 합니다.
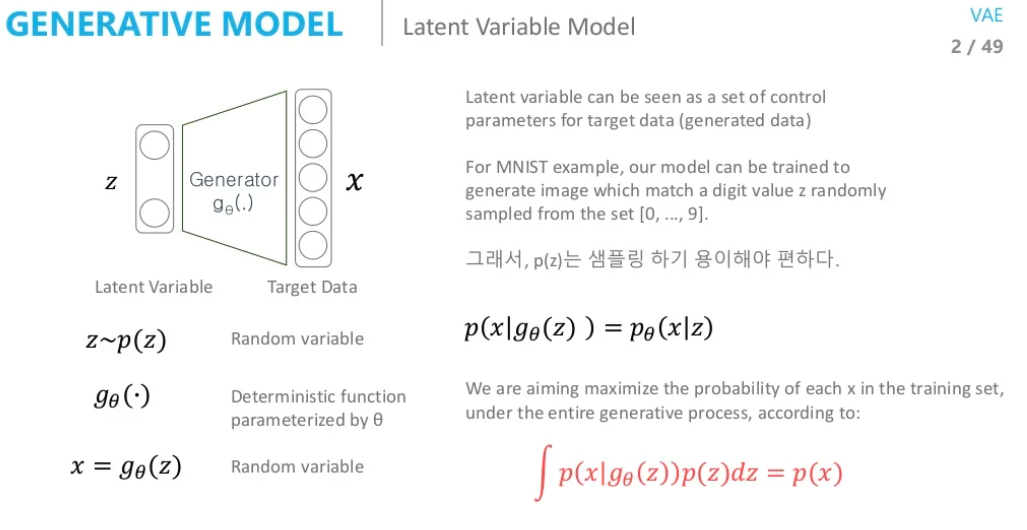
VAE 네트워크의 latent variable 로 부터 데이터 분포를 구해 새로운 데이터를 생성하려고 합니다.

우리는 z를 다루기 쉬운 normal, uniform distrinution과 같이 간단한 분포라고 가정을 하고 sampling을 수행하게 됩니다. manifold에 대해서 설명했을때 이 sub space는 매우 복잡해 보였는데 이렇게 간단한 분포로 가정을 해도 문제가 없을까요? 위 슬라이드를 보시면 가능하다고 합니다. 결론적으로 Deep Neural Network이기 때문에 우리가 구하려고 하는 manifold 분포가 복잡하다 하더라도 처음 한 두개의 layer에서는 manifold를 잘 찾기 위한 역할을 수행한다고 합니다.

그렇다면 해당 가우시안 분포에서 sampling한 데이터를 통해 새로운 데이터를 생성하고 원래 데이터와의 MSE를 직접적으로 하면 되지 않을까요? 정답은 불가능 합니다. 그 이유는 위 이미지를 보시면 알 수 있습니다. 를 실제 데이터 라고 하겠습니다. 는 앞 부분을 자른 이미지이고 는 를 오른쪽으로 한칸 이동시킨 이미지입니다. 의미적으로 와 가 더 가까워야 하고 MSE또한 와 가 더 크길 바랍니다. 하지만 결과는 와 의 MSE값이 더 큽니다. 이처럼 MSE값이 큰게 사실 의미적으로 더 가까울 수 있는 경우가 많기 때문에 Prior 에서 sampling을 하게 되면 문제가 발생합니다.
VI(Variational Inference)
위의 문제점을 정리해보겠습니다.
-
z의 분포를 구하고 싶지만 현실적으로 불가능하다.
-
의미적으로 더 가까운 이상적인 z의 값을 알 수 없다.
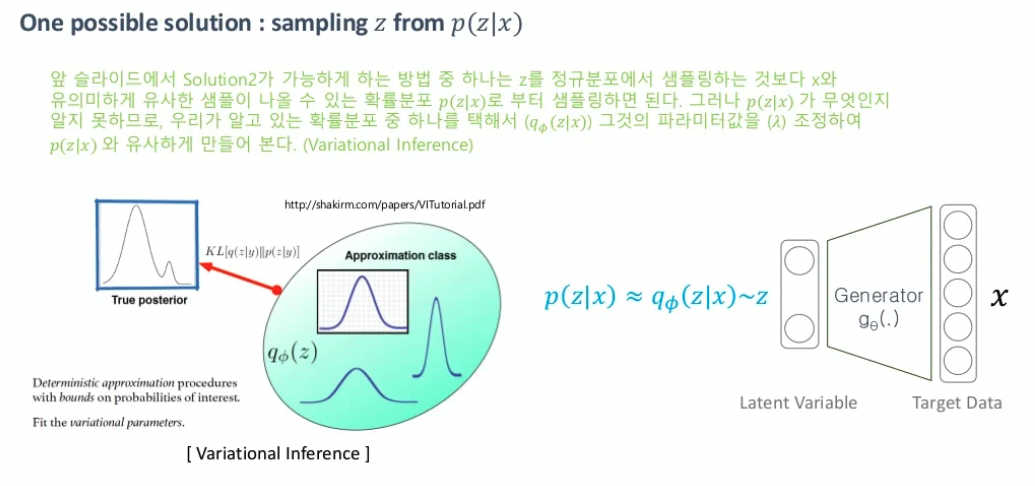
그렇다 보니 그냥 prior 에서 sampling 하지말고 를 통해서 이상적인 를 sampling 할 수 있는 함수를 만들어보자 입니다. 하지만 이상적인 sampling 함수 는 우리가 알 수 없습니다. 따라서 우리는 간단한 분포를 가지는 를 가정하고 이 를 에 approximation하여 를 사용하기로 합니다. 이렇게 모르는 확률분포를 추정을 할때 사용하는 것이 Variational Inference입니다.
ELBO (Evidence LowerBOund)
정보이론편에서 어떤 두 분포의 차이를 계산할때 사용할 수 있는 방법으로 KLD(Kullback-Leibler divergence)를 소개했습니다. 우리의 목적 또한 를 에 근사시키는 것이기 때문에 KLD를 minimize하는 방향으로 학습하면 됩니다.
이 식을 베이지안 정리에 따라 식을 바꿔보겠습니다.
또한 데이터 를 통해 구해야 하기 때문에 로 쓸 수 있습니다.
위의 식에서 는 1이기 때문에 아래와 같이 정리할 수 있습니다.
우변의 은 를 의미하고 는 로 나타낼 수 있습니다.
최종적으로
위와 같은 식으로 정리할 수 있습니다.
우리가 원하는 값을 최소화 하기 위해서는 그 뒤에 있는 수식을 최대화 하면 된다는 접근을 할 수 있습니다. 여기서 최대화를 하려는 수식을 ELBO라 말합니다.
를 최대화 하는 방향으로 학습하는 것은 를 최소화 하는 것과 같은 의미이고 encoder의 parameter를 decoder의 파라미터를 라 했을 때 최종 optimization 함수는 아래와 같습니다.
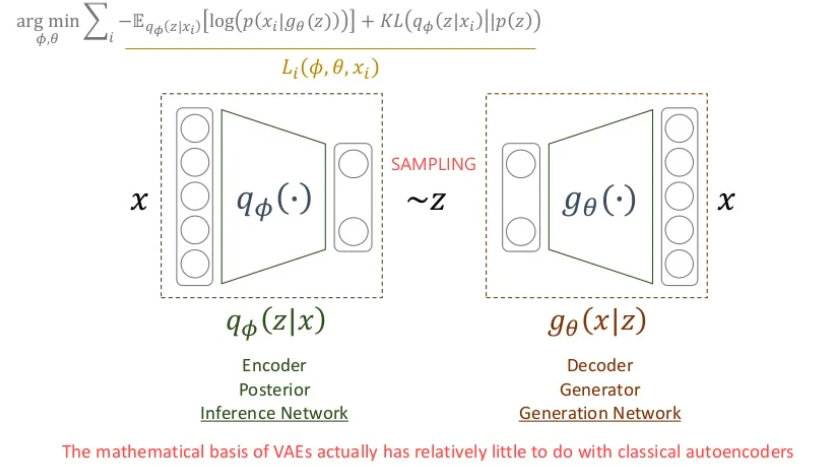
지금까지의 흐름을 정리해 보겠습니다.
-
우리는 generator를 잘 학습하고 싶다.
-
prior에서 sampling하니 성능이 좋지 않다.
-
우리는 이상적인 sampling함수를 구하는 방향으로 문제를 해결하려고 한다.
-
를 모르기 때문에 를 도입했다.
-
이상적인 를 찾는 방법은 term을 대해 maximize하는 것을 의미한다.
-
sampling한 로 부터 가 나올 확률이 최대가 되도록 하는 것은 term을 에 대해 maximize하는 것을 의미한다.
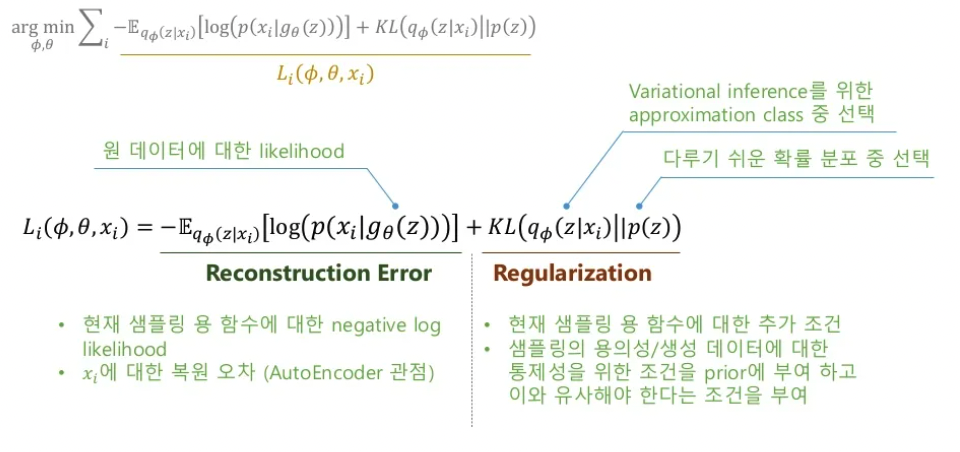
loss function은 위와 같습니다.
Reconstruction Error
로 부터 샘플링 된 가 로 잘 복원되었는지를 판단하는 term입니다.
가 최대값이 될수록 loss는 줄어들도록 학습되게 됩니다.
Regularization
와 prior 가 같아지도록 학습이 진행되게 하는 term입니다.
KL term 계산

가정 1. 를 multivariate gaussian distribution이며 diagonal covariance이 공분산 행렬이다.
가정 2. prior는 multivariate normal distribution이며 평균이 0, 분산이 1이다.
정리하자면 Encoder의 네트워크로 를 평균이 0, 분산이 1인 정규분포 로 approximation하는 것 입니다.
그렇다면 KL term을 계산만 할 수 있으면 코드로 구현을 할 수 있는데 계산하는 방법은 아래와 같습니다.

Reparameterization Trick
다음은 Reconstruction Error에 대한 계산입니다.
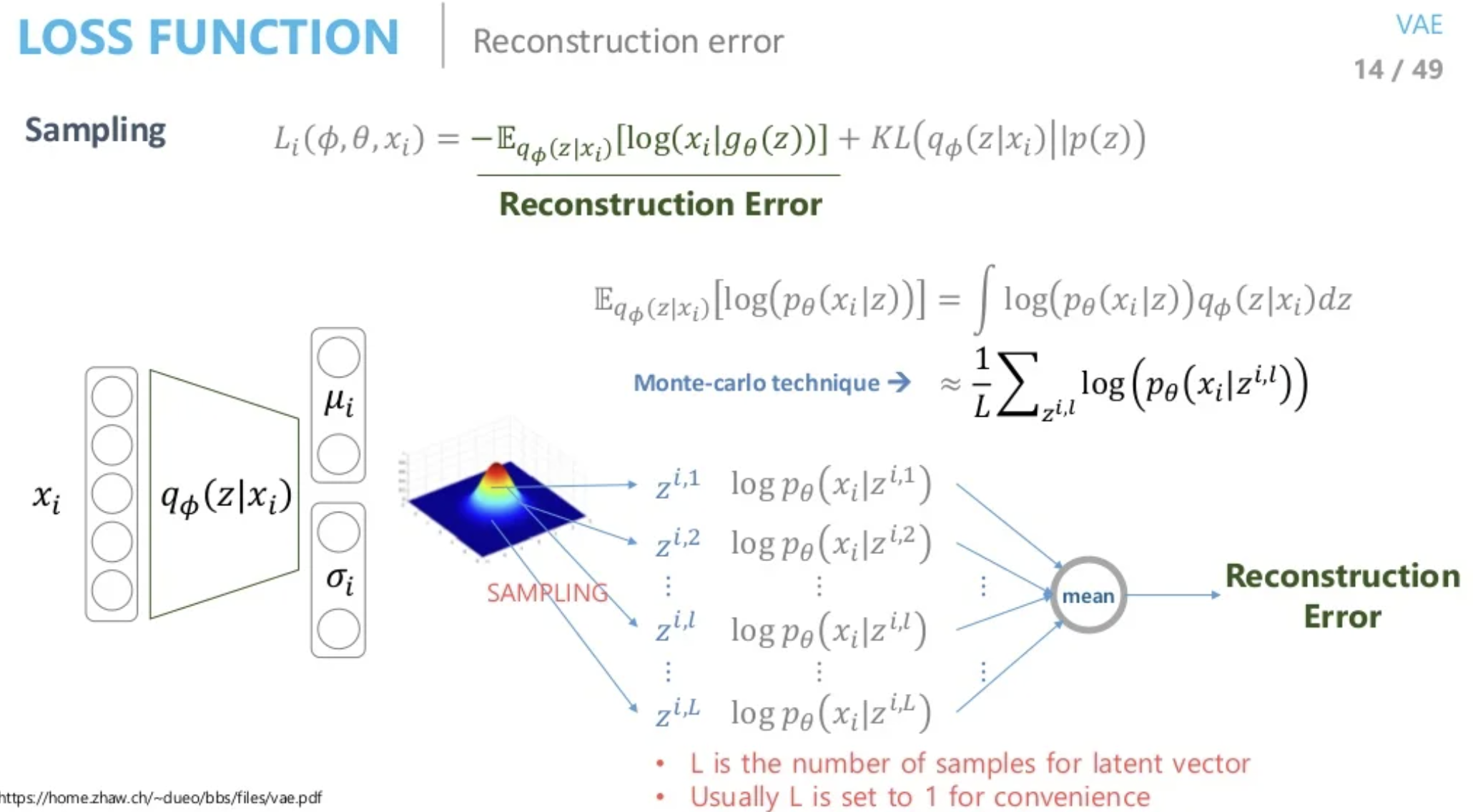
는 가우시안으로 가정을 한 상태이므로 와 가 정해진 상태입니다. 이 분포를 통해서 를 sampling하게 되는데 모든 에 대하여 적분을 하는것은 불가능 하기 때문에 Monte Carlo 기법을 사용하여 충분히 많은 개를 평균값을 사용하게 됩니다. 이 개를 계산하는 작업도 상당히 오래걸리기 때문에 개가 아닌 1개만 sampling하고 추출된 가 전체를 대표한다는 가정을 하게 됩니다. 이 sample을 decoder에 태우게 되고 likelihood를 최대화 하도록 적절한 파마리터를 찾게 됩니다. 하지만 여기서 마지막 문제는 sampling을 하는 단계입니다. 이 단계는 back propagation할때 문제가 되는데 sampling은 randomly한 방식이기 때문에 매번 학습할때마다 바뀌게 되어 계산이 불가능합니다. 이 문제를 피하기 확률분포를 그대로 유지하며 back propagation이 가능하도록 하게 만드는 기술이 Reparameterization Trick 입니다.

randomly한 sampling이 아닌 평균이 0, 분산이 1인 분포에서 sampling한 후 encoder를 통해 구한 평균과 분산을 각각 더하고 곱하여 사용하여 문제를 해결할 수 있습니다.

decoder의 확률분포를 베르누이 분포라고 가정하면 결국 cross entropy를 의미하는 식이 됩니다.

decoder의 확률분포를 가우시안 분포라고 가정하면 MSE를 의미하는 식이 됩니다.
정리
마지막 최종 정리를 해보겠습니다.
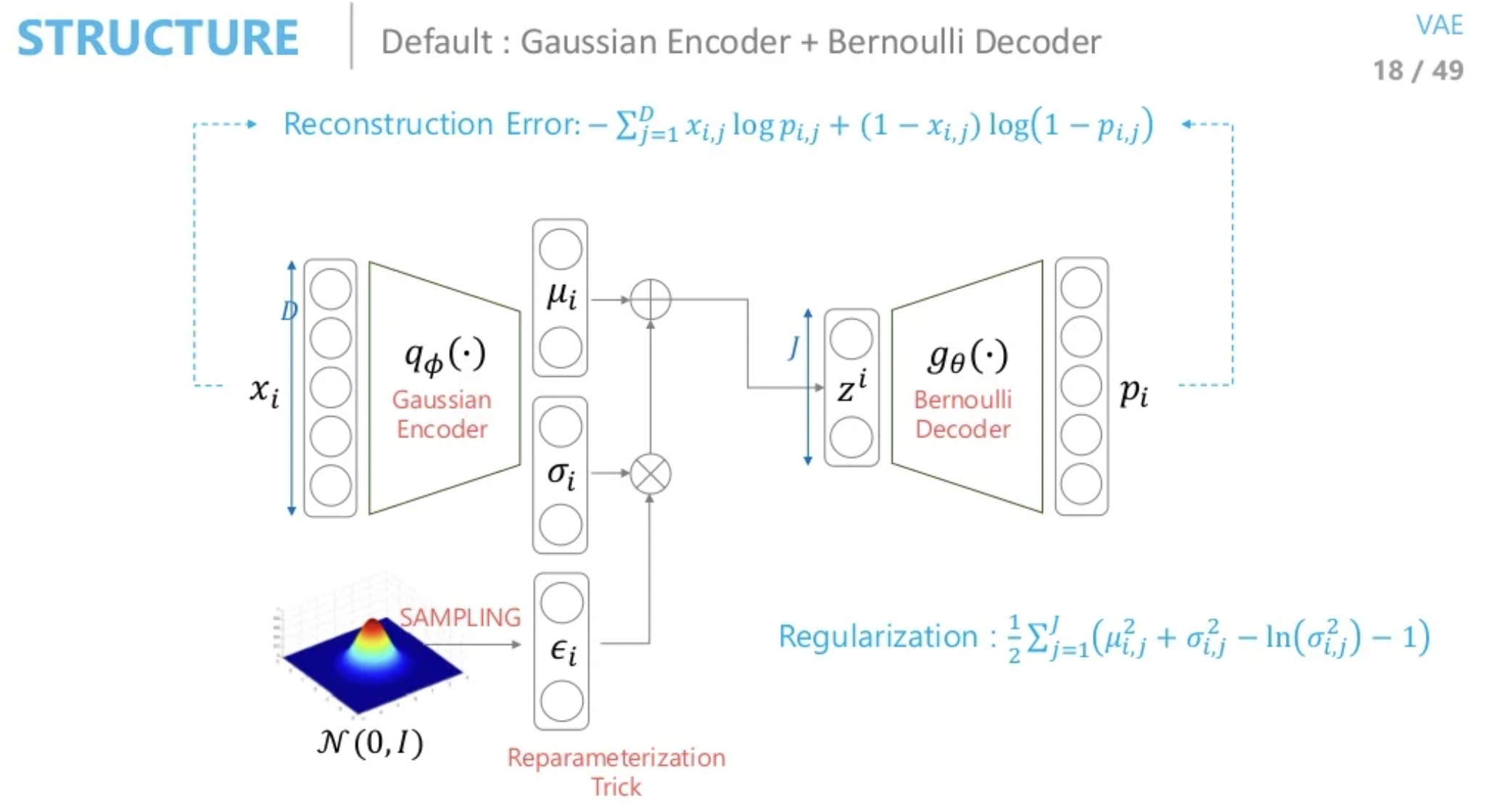
- Encoder(Gaussian) + Decoder(Bernoulli)
-
데이터를 생성하기 위해 적절한 를 sampling할 수 있는 함수를 찾고 싶다.
-
그냥 찾을 수 없으니 를 evidence로 사용하여 를 로 근사한다.
-
가우시안이라고 가정하면 와 를 찾아 reparameterization을 통해 sampling 한다.
-
sample 를 decoder에 태우는데 베르누이를 따른다 하면 네트워크의 출력값과 입력값이 cross entropy로 계산된다.
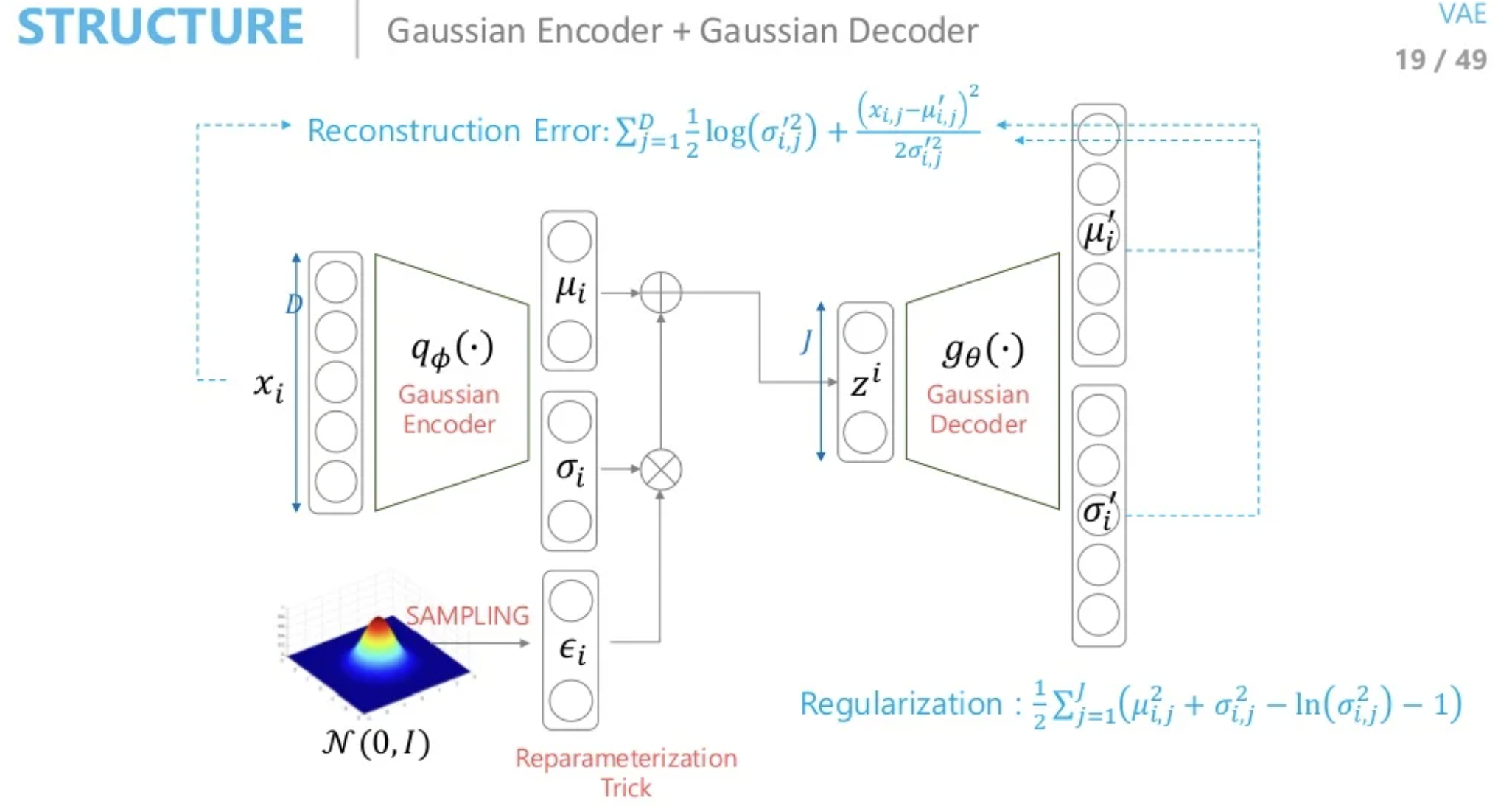
- Encoder(Gaussian) + Decoder(Gaussian)
Regularization은 바뀌지 않지만 네트워크 출력값으로 평균과 분산을 추정할 경우 위와 같은 식으로 Reconstruction Error가 정의됩니다.
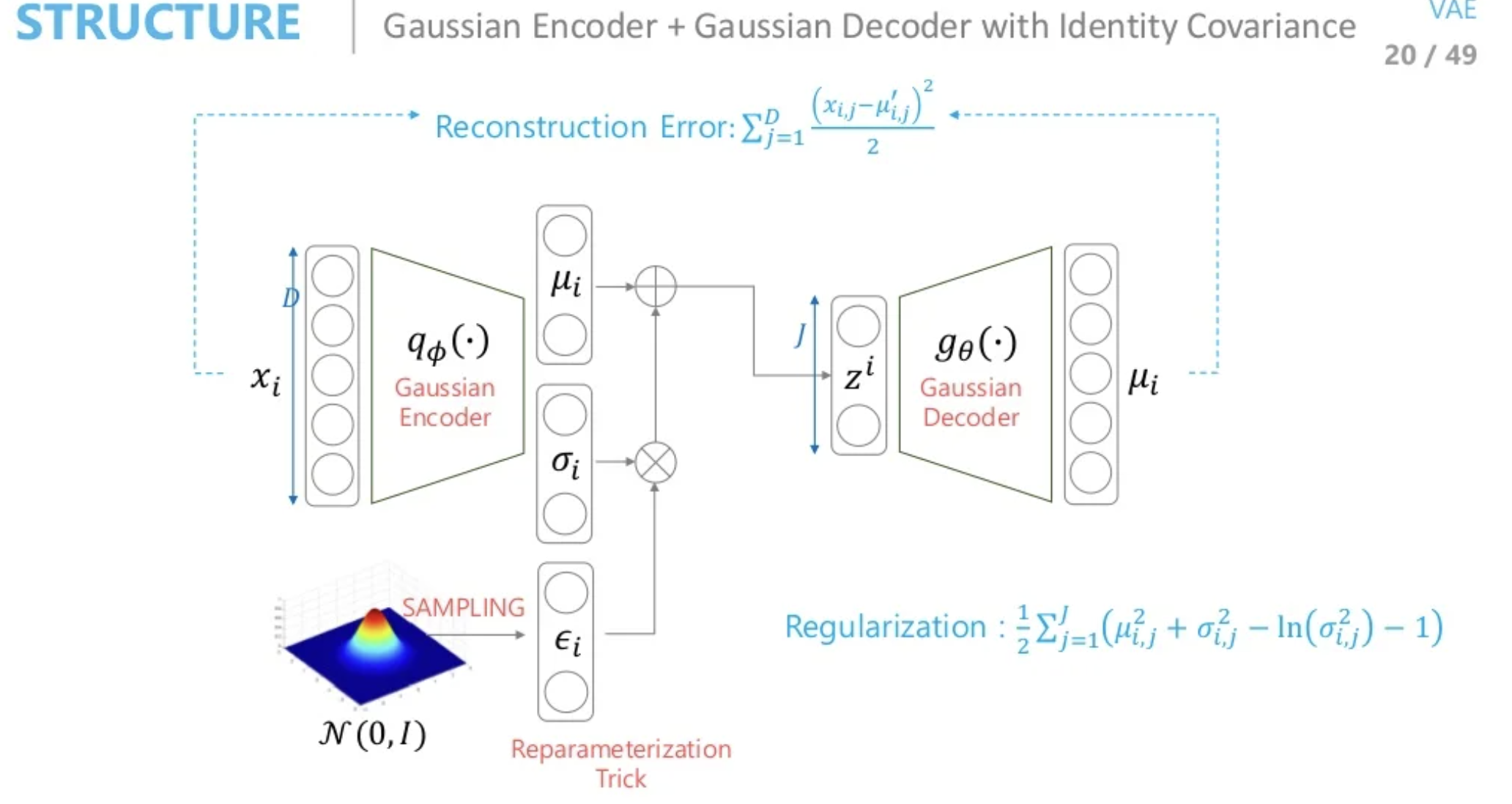
- Encoder(Gaussian) + Decoder(Gaussian) with identity Covariance
네트워크 출력값으로 평균만 추정할 경우 Reconstruction Error는 MSE와 같게 됩니다.
지금까지 AE부터 VAE까지 알아보았는데 개념적으로는 애초에 서로 목적이 다르지만 코드상에선 뭐가 다를까요?
코드상의 차이점은 1개의 라인만 다르다고 볼 수 있습니다. VAE의 Reconstruction Error는 sampling하는 z를 사용하는 것을 제외하면 AE도 똑같습니다. 차이점은 바로 KL을 통해서 를 prior의 분포와 같아지도록 학습했다는 점입니다.
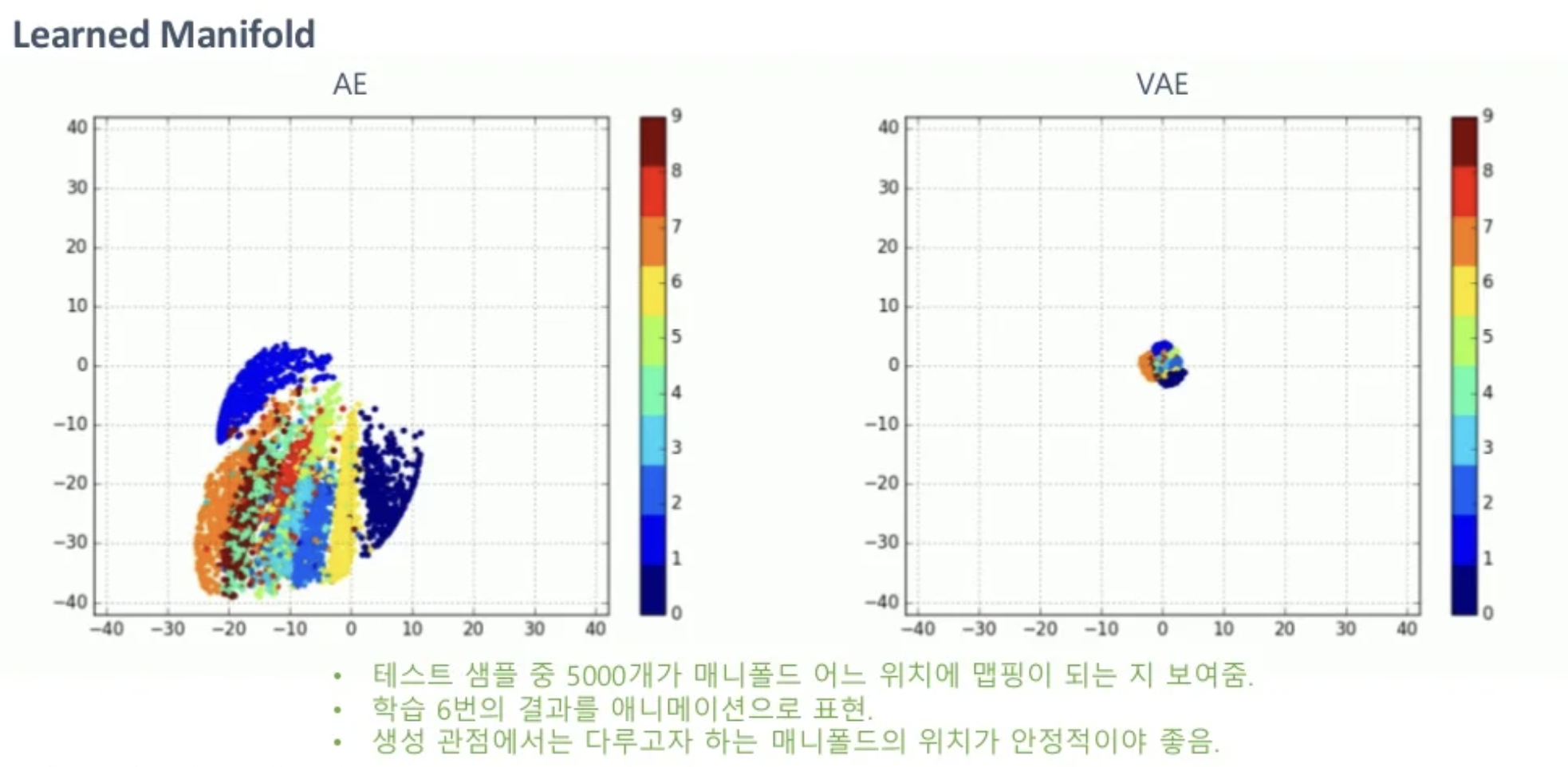
따라서 학습이 끝났을 때 AE와 VAE의 공간을 보면 위와 같습니다. AE는 학습을 할때마다 공간의 위치가 계속 바뀌게 되지만 VAE는 normal하게 됩니다. 따라서 데이터를 생성하고 싶을때 AE는 z를 sampling할 수 없고 VAE는 prior에서 sampling하면 됩니다.
지금까지 한 두번 보고는 이해하기 힘든 VAE를 정리해보았습니다.
다음에는 아직 남은 CVAE, AAE에 대해서 정리해보겠습니다.