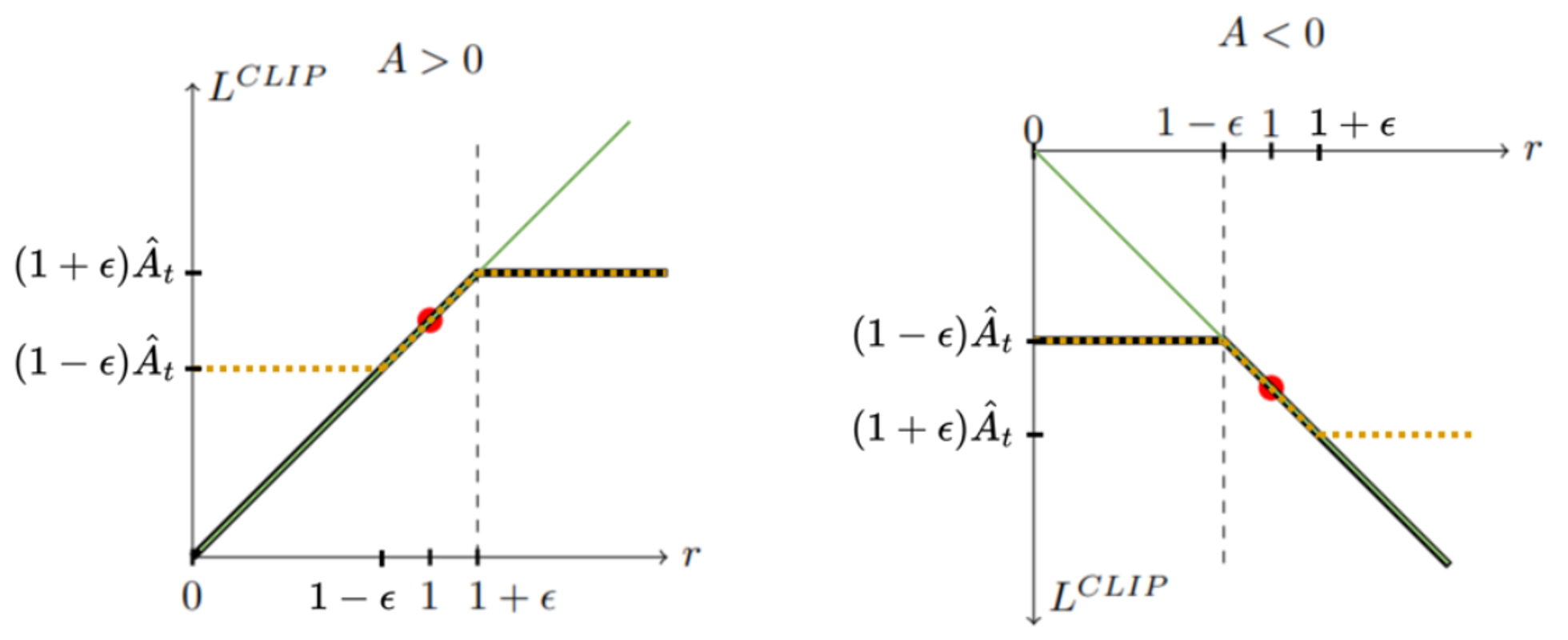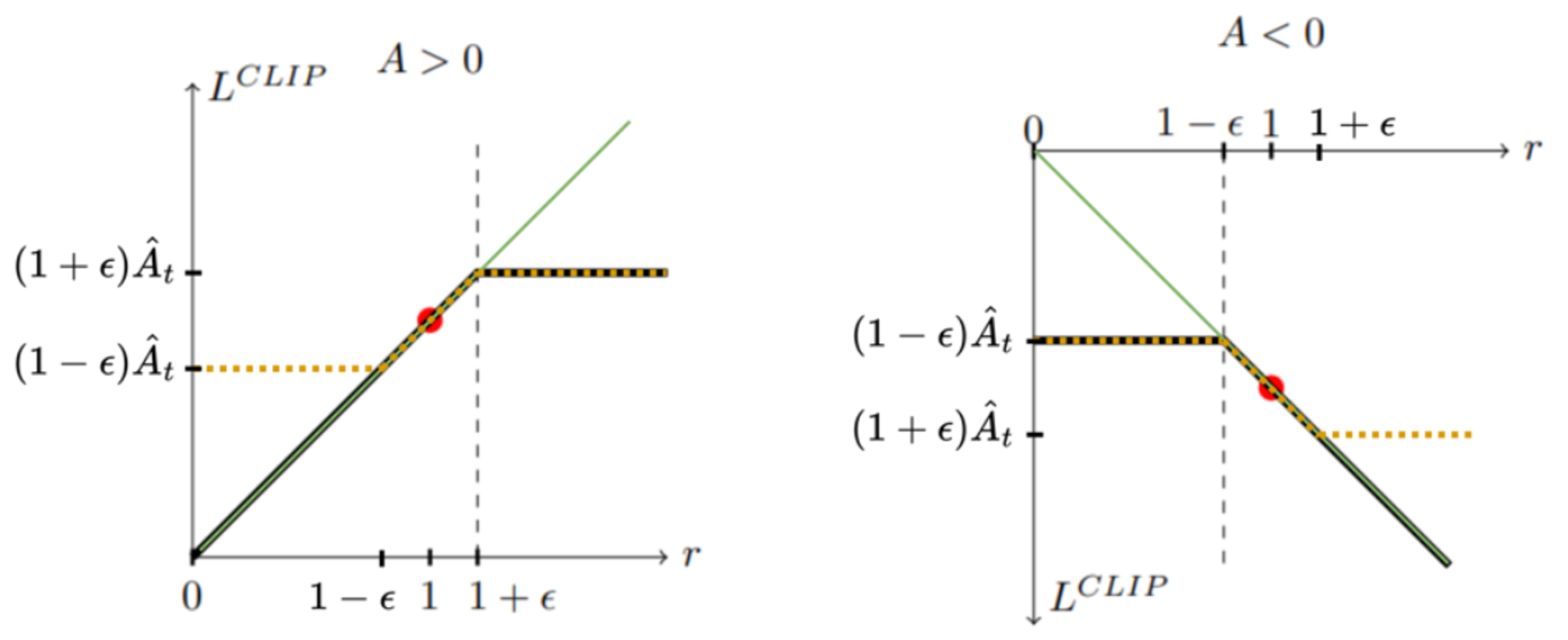Proximal Policy Optimization (PPO) 간단 정리

Trust Region PO vs Proximal PO

• PPO는 이전 TRPO 알고리즘을 조금 더 실용적으로 발전시킨 논문
  • Policy gradient 계열의 알고리즘으로, 성능이 우수하면서도 구현이 간단하여 performance와 complexity 간의 밸런스가 잘 잡힌 알고리즘으로 알려짐
• PPO와 TRPO는 주어진 데이터로 현재 policy를 최대한 큰 step만큼 빠르게 향상시키면서, 너무 발산할 정도로 큰 step으로 업데이트하는 것은 억제하고자 하는 동일한 motivation을 가짐

• TRPO에서는 objective term $\frac{\pi_\theta(a|s)}{\pi_\text{old}(a|s)}\hat{A}_t$를 최대화하면서, penalty term $KL[\pi_\text{old}||\pi_\theta]$를 최소화하는 것을 목표
  • 즉 목적식을 통해 policy의 improvement step을 최대한 크게 가져가면서, 동시에 penalty term에서 old policy와 new policy 간의 차이가 너무 커지지 않도록 KL divergence를 통해 제한하는 역할까지
• PPO에서는 objective term $\frac{\pi_\theta(a|s)}{\pi_\text{old}(a|s)}\hat{A}_t$을 최대화하는 부분은 TRPO와 동일하나 penalty term을 KL divergence 대신 clipping으로 변경
  • 이를 통해 second-order method가 아닌 first-order method로 계산이 가능해져 구현 상의 실용성을 얻게 됨

PPO의 메커니즘

Surrogate Objective

• Policy gradient 알고리즘은 목적 함수 $J(\pi_\theta)$를 최대화하기 위해 policy gradient $\nabla J$ 방향으로 정책 $\pi_\theta$를 업데이트
  $J(\pi_\theta)=\mathbb{E}_{s\sim\rho_{\pi_\theta},a\sim\pi_\theta}[A_{\pi_\theta}]=\sum_s\rho_{\pi_\theta}(s)\sum_a\pi_\theta(a|s)A_{\pi_\theta}(s,a)$
  • 목적함수를 어떻게 정의했는지에 따라 policy gradient는 다양하게 표현할 수 있으며, advantage $A_{\pi_\theta}$를 이용한 목적함수는 위와 같음
  • $\rho_{\pi_\theta}(s)=P(s_0=s)+\gamma P(s_1=s)+\gamma^2 P(s_2=s)+\cdots$는 discounted visitation frequencies로 state가 $s$를 방문할 확률
• 여기서 $\pi_\text{old}\rightarrow\pi_\theta$로 policy가 충분히 작게 업데이트 된다면, $\rho_{\pi_\theta}(s)$를 $\rho_{\pi_\text{old}}(s)$로 대체할 수 있고, 이를 surrogate objective $L(\pi_\theta)$라고 정의
  $J(\pi_\theta)=\sum_s\rho_{\pi_\theta}(s)\sum_a\pi_\theta(a|s)A_{\pi_\theta}(s,a) \\ L(\pi_\theta)=\sum_s\rho_{\pi_\text{old}}(s)\sum_a\pi_\theta(a|s)A_{\pi_\theta}(s,a)$
  • 따라서, policy가 충분히 작은 만큼만 변화했을 때는 $J(\pi_\theta)$ 대신 $L(\pi_\theta)$을 이용해 최적화를 수행해도 동일한 결과를 얻을 수 있음
  • 이 때문에 policy update에 대한 constraint가 추후 penalty term으로 추가됨

Importance Sampling

[Importance Sampling]
함수 $f(x)$의 확률분포 $p(x)$의 기댓값을 구할 때 $\mathbb{E}_{x\sim p}[f(x)]=\int f(x)p(x)dx$를 수식적으로 계산하기 어려운 경우, 큰 수의 법칙에 따라 sampling을 통해 $x^{(n)}$을 추출한 후 기댓값을 근사하는 방법을 Monte Carlo 기법이라고 한다.
Importance sampling은 이러한 상황에서 본래의 분포 $p(x)$가 아닌, 다른 확률분포 $q(x)$에서 추출된 sample들을 이용해 기댓값 $\mathbb{E}_{x\sim p}[f(x)]$를 계산하는 방법이다.

$\mathbb{E}_{x\sim p}[f(x)] \simeq \underset{\text{Monte Carlo}}{\underbrace{\frac{1}{N}\sum^N_{n=1}f(x^{(n)})}} \simeq\underset{\text{Importance Sampling}}{\underbrace{\frac{1}{N}\sum^N_{n=1}\frac{p(x)}{q(x)}f(x^{(n)})}}$

$x\sim p$로부터의 sampling이 불가능하거나 비효율적인 경우 사용한다.

• Sample 기반 추정을 위해 surrogate objective를 expectation으로 표현하고, importance sampling을 활용해 식을 변형하면 아래와 같이 나타낼 수 있음
  $L(\pi_\theta) =\mathbb{E}_{s\sim\rho_{\pi_\text{old}},a\sim\pi_\theta}[A_{\pi_\theta}(s,a)] =\mathbb{E}_{s\sim\rho_{\pi_\text{old}},a\sim\pi_\text{old}}[\frac{\pi_\theta(a|s)}{\pi_\text{old}(a|s)}A_{\pi_\theta}(s,a)]$
  • Importance sampling을 통해 기존 policy $\pi_\text{old}$로부터 생성된 sample들을 이용해 업데이트 된 policy $\pi_\theta$를 평가할 수 있음
  • 즉, 새로 업데이트 된 policy를 평가할 때마다 새로운 sample을 생성할 필요 없이 old policy로부터 생성된 sample을 재사용할 수 있다는 뜻
• $\hat{\mathbb{E}}_t$가 sample 평균을 의미할 때, 위 식은 아래 처럼 표현될 수 있음
  $L(\theta)=\hat{\mathbb{E}}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_\text{old}(a_t|s_t)}\hat{A}_t]$
  • 이로 인해 PPO는 한 번의 episode에서 획득한 sample들을 여러 번 재사용해 policy 업데이트를 할 수 있음

Clipping

• Policy의 과도한 업데이트를 막기 위해 PPO는 clipping과 adaptive KL penalty의 두 방식을 제안했으나, 일반적으로 clipping 방식이 널리 알려져 있음

• Surrogate objective에서 $r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_\text{old}(a_t|s_t)}$로 치환할 수 있고, 이는 특정 action을 취할 old policy와 new policy의 확률 비율을 의미

  • 때문에 policy가 업데이트 되지 않아 $\pi_\theta=\pi_\text{old}$인 경우, $r_t(\theta)=1$이 성립하게 됨

• Clipping은 이 $r_t(\theta)$를 $[1-\epsilon,1+\epsilon]$ 사이로 제한해 policy가 업데이트되어도 특정 action을 수행할 확률이 너무 급격히 증감하는 것을 억제

  $L^\text{CLIP}(\theta)=\min(r_t(\theta)\hat{A}_t,\;\text{clip}(r_t(\theta),1-\epsilon,1+\epsilon))$
  • Clipping은 최종적으로는 위 수식처럼 $r_t(\theta)\hat{A}_t$와 $\text{clip}(r_t(\theta),1-\epsilon,1+\epsilon)$ 중 더 작은 값을 선택
  • 결과적으로 advantage가 양수일 때는 $1+\epsilon$, 음수일 때는 $1-\epsilon$에 의해서만 clipping이 발생

• $L^\text{CLIP}$은 PPO가 최대화하고자 하는 목적 함수

  

  • $A>0$일 때는 $r$을 증가시키는 것이 좋은 action을 선택할 확률을 강화시키는 것으로 $L^\text{CLIP}$이 증가
  • $A<0$일 때는 $r$을 감소시키는 것이 나쁜 action을 선택할 확률을 약화시키는 것으로 $L^\text{CLIP}$이 증가
  • 여기서 PPO는 $A>0$일 때 $1+\epsilon$으로 $r$을 clipping, $A<0$일 때 $1-\epsilon$으로 $r$을 clipping 해줌으로써, 한 번에 너무 많은 $L^\text{CLIP}$이 증가하는 방향으로 policy가 업데이트되는 것을 피하고자 함

Generalized Advantage Estimation (GAE)

• Trajectory로부터 추정된 기존의 advantage는 high variance error를 가지고 있음
  $\text{Advantage function}: \quad\hat{A}_t=-V(s_t)+r_t+\gamma r_{t+1}+\cdots+\gamma^{T-t+1}r_{T-1}+\gamma^{T-t}V(s_T) \\ \text{(Truncated) GAE}: \quad\hat{A}_t=\delta_t+(\gamma\lambda)\delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\delta_{T-1} \\ \quad\text{where}\quad\delta_t=r_t+\gamma V(s_{t+1})-V(s_t)$
  • PPO에서는 기존의 advantage variance를 낮추기 위해 truncated GAE를 사용
  • GAE는 파라미터 $\lambda$의 조절을 통해 bias-variance 사이의 trade-off를 조절 ($\lambda=0$일 때 high-bias/low-variance, $\lambda=1$일 때 low-bias/high-variance)

PPO 알고리즘

[Pseudo code of PPO algorithm]

for iteration=1, 2, ..., N do
    for actor=1, 2, ..., N do
        Run policy π_{θ_old} in environment for T timesteps
        Compute advantage estimates Â_1, ..., Â_t
    end for
    Optimize surrogate L w.r.t. θ, with K epochs and minibatch size M ≤ NT
    θ_old ← θ
end for

• PPO는 environment와의 상호 작용 시 한 번의 step만 진행해야할 필요는 없으며, 고정된 길이의 trajectory (또는 episode) 단위로 상호작용할 수 있음
  • 또한 여러 actor를 병렬 수행해 sample을 획득할 수 있음
  • 따라서, 해당 과적으로는 $N$개의 actor가 environment와 상호작용하여 $T$ timesteps 길이의 sample 획득
• 결과적으로 $NT$개의 timesteps 데이터가 수집되며, 이를 바탕으로 surrogate objective를 계산
  • PPO는 importance sampling으로 surrogate objective를 최적화하기 위한 파라미터 업데이트를 $K$ epochs 만큼 반복하여 수행할 수 있게 되고, 한 번의 iteration이 끝나면 다시 environment와의 상호 작용 수행을 위해 과정을 반복하게 됨