[ML] 의사결정나무

PhilAI·2023년 2월 6일

머신러닝 쉽게 배우자! 💻

목록 보기

4/5

엔트로피란?

예시를 들어서 알려드리면 쉬울 것 같아요! 확률에 빠지지 않는 동전 예시를 들어볼게요. 한 동전은 얼굴면 숫자면으로 이루어져 있습니다.
Case 1
동전은 던졌을때, 각 면이 나올 확률은 어떻게 될까요?
얼굴: 50%
숫자: 50%
어떤 면이 나올지를 확신이 없기때문에 불확실성이 높습니다.

Case 2
동전에 두면 모두 얼굴그림이 박혀있다면 사람그림이 나올 확률은 얼마나 될까요?
이 경우 어떻게 던지든 간에 사람그림이 나오기 때문에 불확실성이 없습니다.

Case 3
동전이 굽어있어 던졌을 때 얼굴면과 숫자면이 나올 확률을 아래와 같습니다:
얼굴: 90%
사진: 10%
이 경우 불확실성이 있지만 case 1의 불확실성보단 낮을 겁니다.

이처럼 특정 사건의 불확실성을 나타내는 정도를 엔트로피(Entropy)로 나타내게 됩니다. 엔트로피의 공식은 아래와 같습니다:

$H(X) = - \sum_{i=1}^{n}p_i\log_2p_i$

그렇다면 다시 동전 예시를 들어 각 케이스의 엔트로피를 계산해보도록 할까요?

케이스	얼굴면 확률	숫자면 확률	공식대입	엔트로피
1	50%	50%	$-(0.5\log_20.5 + 0.5\log_20.5)$	1
2	100%	0%	$-(1.0\log_21.0 + 0\log_21.0)$	0
3	90%	10%	$-(0.9\log_20.9 + 0.1\log_20.1)$	0.47

여기서 두가지 사실을 알수가 있습니다.
1. 엔트로피가 높을수록 불확실성이 높고, 엔트로피가 낮을수록 불확실성이 낮다.
2. 엔트로피는 0과 같거나 크고 1과 같거나 작다. ( $0 \leq entropy \leq$ )

동전은 경우 사람면, 숫자면으로 해서 분류가 기준이 binary합니다.
이 경우 최대 엔트로피는 1이지만 8개의 분류로 나뉘는 경우는 어떻게 될까요?
$8= 2^3$
최대 엔트로피는 "3" 입니다.
그렇다면 16개의 분류로 나뉘는 경우는 어떻게 될까요?
$16= 2^4$
최대 엔트로피는 "4" 입니다.

의사결정나무

엔트로피의 개념을 익혔다면, 이를 활용한 "의사결정나무"를 알아보도록 하겠습니다. 말 그대로 가지를 그려 데이터를 특정 기준으로 나누는 것을 의사결정 나무 트리라고 합니다.

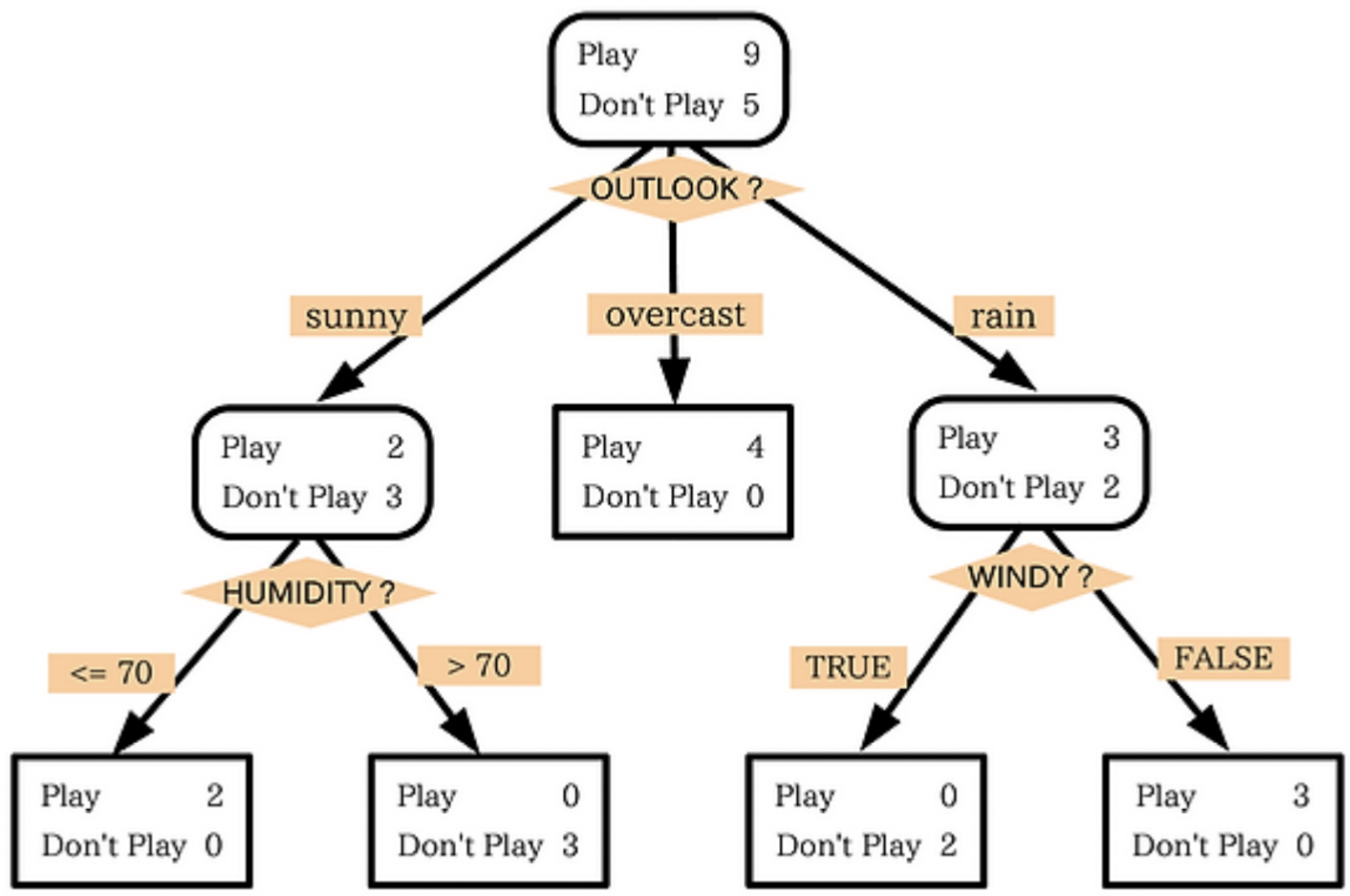
의사결정나무는 보시다시피 매우 직관적이라 결과를 해석하고 예측하기가 엄청 쉽다는 장점을 갖습니다.
하지만 단점도 존재합니다. 연속형 변수를 범주형 값으로 취급하기 때문에 분리의 경계점 부근에서 에측 오류가 클수 있습니다. 이 뿐아니라 노이즈 데이터에 영향을 크게 받습니다... :(

의사결정나무를 만들때 가장 중요한 것은 더 중요한 특징을 구분해주는 것이 뽀인트입니다! 여기서 중요한 특징이라는 것은 "확실한" 특징을 말합니다.
이부분도 이해를 돕고자 예시를 들어서 설명을 해보겠습니다.

아래의 데이터은 두가지 특징으로 분류가 가능합니다.
1. 특정 사람이 군대를 갔다왔는지.
2. 짧은 머리스타일을 가지고 있는지.
이 두 특징중 어떤 특징이 의사결정나무에 더 좋은 특징인지를 알아보도록 할겠습니다.

사람	군대을 갔다왔는지	짧은 머리스타일을 가지고 있는지	성별
1	yes	no	남
2	no	no	여
3	yes	no	남
4	no	yes	여
5	yes	no	남
6	no	no	여

1. 군대 특징을 분류했을 때

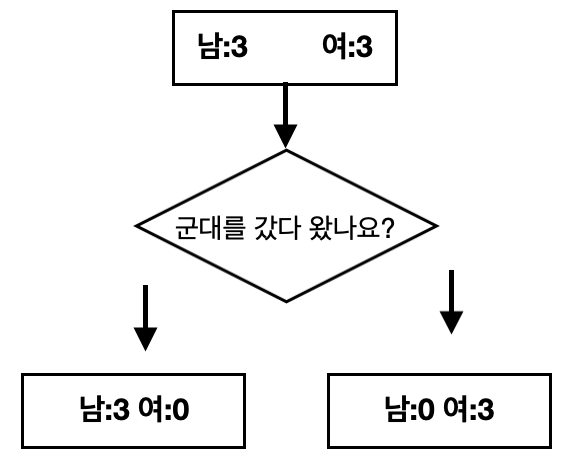
남:3 여:0) $\frac{3}{6}(-\frac{3}{3}\log_2\frac{3}{3} - \frac{3}{3}\log_2\frac{3}{0})$
남:0 여:3) $\frac{3}{6}(-\frac{3}{3}\log_2\frac{3}{3} - \frac{3}{3}\log_2\frac{3}{0})$

둘값을 더하면, 전체 엔트로피 값은"0"입니다.

2. 짧은 헤어스타일의 여부로 분류했을 때

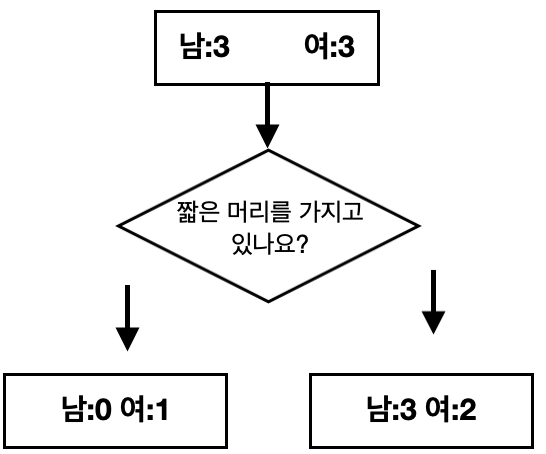
남:0 여:1) $\frac{1}{6}(-\frac{0}{1}\log_2\frac{0}{1} - \frac{1}{1}\log_2\frac{1}{1})$
남:3 여:2) $\frac{5}{6}(-\frac{3}{5}\log_2\frac{3}{5} - \frac{2}{5}\log_2\frac{2}{5})$