[ML] 로지스틱 회귀 (Logistic Regression)

PhilAI·2023년 8월 13일

머신러닝 쉽게 배우자! 💻

목록 보기

3/5

📌 로지스틱 회귀란?

로지스틱 회귀는 데이터를 분류하는 데 사용되는 알고리즘입니다. 이진 분류 문제에서 두 개의 가능한 클래스 중 하나에 데이터를 할당합니다. 예를 들어, 이메일이 스팸인지 아닌지를 예측하거나, 환자가 질병을 가지고 있는지 없는지를 판단하는 데 사용될 수 있습니다.

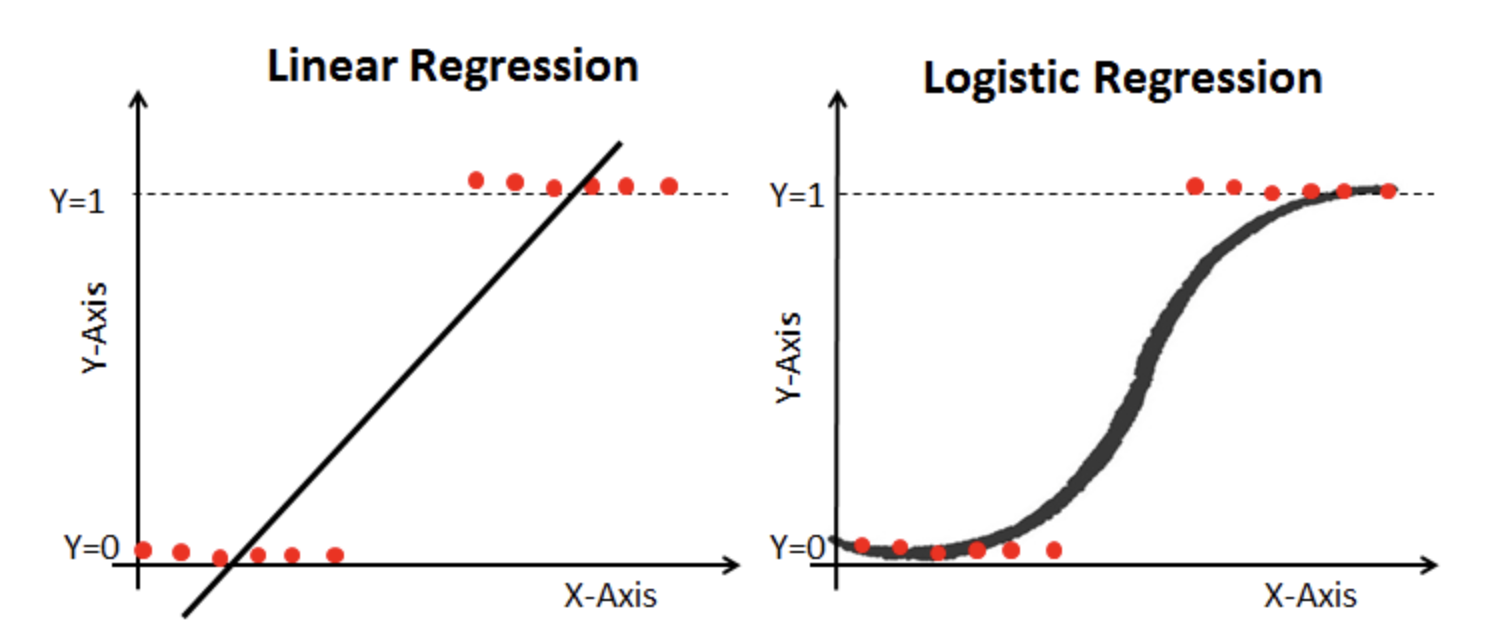
로지스틱 회귀에서 데이터가 특정 범주에 속할 확률을 예측하기 위해 아래와 같은 단계를 거칩니다. 간단하게 설명해보겠습니다.

1. 초기화

모든 속성(또는 특성)의 계수와 절편을 0으로 초기화합니다.

2. 로그-오즈 계산

각 속성의 값에 해당 속성의 계수를 곱하여 모든 속성의 계수를 합한 선형 결합을 계산합니다. 이는 로그-오즈를 생성하는 단계입니다.
로그-오즈는 입력 데이터의 가중치 합을 나타냅니다.

3. Sigmoid 함수 적용

로그-오즈 값을 sigmoid 함수에 넣어서 [0, 1] 범위의 확률 값을 구합니다.
sigmoid 함수는 S자 모양의 곡선으로, 입력 값에 대해 0과 1로 수렴하게 됩니다.
이 확률은 특정 데이터가 특정 범주에 속할 확률을 나타냅니다.

간단하게 말하면, 로지스틱 회귀는 데이터의 속성과 각 속성의 계수를 조합하여 선형 결합을 계산한 후, 이를 sigmoid 함수에 넣어서 확률을 추정하는 과정입니다. 이를 통해 데이터가 특정 범주에 속할 확률을 예측할 수 있습니다.

(이해 못해도 괜찮아요! 찬찬히 설명할거에요 😃 )

📌 오즈란?

오즈(Odds)는 어떤 사건의 발생 확률과 그 사건이 발생하지 않을 확률의 비율을 나타내는 개념입니다. 오즈의 공식은 아래와 같습니다

오즈 = P / (1 - P)

예를 들어, 동전 던지기를 생각해봅시다.

동전의 앞면이 나올 확률을 P라고 하면, 동전의 뒷면이 나올 확률은 1 - P입니다. 이때, 오즈는 다음과 같이 정의됩니다:
동전이 공평하다면, 즉 앞면과 뒷면이 나올 확률이 각각 0.5라면:
오즈 = 0.5 / (1 - 0.5) = 1

즉, 앞면이 나올 확률과 뒷면이 나올 확률의 비율은 1입니다. 오즈가 1이라는 것은 앞면과 뒷면의 확률이 동일하다는 의미입니다.

더 복잡한 예시를 들어볼겠습니다.

축구 경기에서 특정 팀이 이길 확률을 생각해봅시다. 특정 팀의 승리 확률을 P라고 하면, 팀이 패배할 확률은 1 - P입니다. 오즈의 공식에 대입해봅니다.
만약 특정 팀의 승리 확률이 0.7이라면:
오즈 = 0.7 / (1 - 0.7) = 2.333

이 경우, 오즈가 2.333이므로 해당 팀의 승리 오즈는 2.333배입니다.다르게 말해 팀의 승리 오즈가 2.333배라는 것은 팀이 승리할 확률이 패배할 확률보다 약 2.333배 높다는 의미입니다.

📌 오즈비란?

오즈비(Odds Ratio)는 두 개의 다른 그룹 또는 조건 간의 오즈를 비교하는 데 사용되는 개념입니다. 두 그룹의 오즈비를 계산하면 어떤 그룹이나 조건이 다른 그룹이나 조건보다 얼마나 더 높은 확률로 특정 사건이 발생하는지를 파악할 수 있습니다.

오즈비 = (오즈 그룹 A) / (오즈 그룹 B)

예시를 들어서 설명해보도록 하겠습니다!!
한 연구에서 특정 질병에 걸릴 가능성과 유전적인 요인 간의 관련성을 조사하고자 합니다. 연구 대상은 500명으로, 250명은 해당 질병에 걸린 사람들(질병 그룹), 나머지 250명은 건강한 사람들(비질병 그룹)입니다.

	질병에 걸림 (A)	질병에 걸리지 않음 (B)	합계
질병 그룹	150	100	250
비질병 그룹	50	200	250
-----------------	----------------	-----------------------	-----------
합계	200	300	500

질병과 비질병의 오즈를 계산해봅시다:

질병 그룹의 오즈: (0.6 / 0.4) = 1.5
비질병 그룹의 오즈: (0.2 / 0.8) = 0.25

오즈비의 계산을 해봅시다. 오즈비의 공식은 앞에도 말씀드렸다시피 두 그룹의 비율을 나누면됩니다.

오즈비 = (질병 그룹의 오즈) / (비질병 그룹의 오즈) = 1.5 / 0.25 = 6

오즈비가 6이라는 것은 질병 그룹에서 해당 질병에 걸릴 확률이 비질병 그룹에 비해 6배 높다는 것을 나타냅니다. 오즈비가 1보다 크므로 이 두 그룹 간에 양의 상관 관계가 있다고 해석할 수 있습니다. 즉, 유전적인 요인이 해당 질병과 관련이 있을 가능성이 높습니다.

📌 로짓

로짓(Logit)은 오즈비에 로그를 씌운 것과 같습니다. 우선 앞에 사용한 예시를 들어 수학적으로 설명해보겠습니다 (다 이해하실 필요 없습니다!! 뒤에 딱 이해하게끔 설명해뒀습니다)

저희가 가지는 종속변수는 0과 1입니다. 다르게 말해 있다/없다, 이다/아니다, 발병한다/발병하지 않는다로 의미할 수 있습니다.
이러한 경우에 가장 극단적인 두 경우가 존재합니다.

1) 모두가 질병에 걸렸다 -> 오즈비 최솟값인 0이 된다 -> 로그변환 -> $\lim_{x \to 0^+} \ln(x) = -\infty$
2) 모두가 질병에 걸리지 않았다. -> 오즈비 최댓값인 무한대가 된다. -> $\lim_{x \to \infty} \ln(x) = \infty$

(주의! 1%(1-1)이라는 계산은 불가능 하지만 분모를 0에 가까운 0이 아닌 작은 수라고 가정한다. 그러경우 오즈비는 무한대가 된다.)

극단적이 두 경우를 종합해서 정리하자면 오즈비에 로그를 씌우면 로짓이 되는데, 로짓이 되면 0,1의 값을 가지는 종속변수가 음수 무한대에서 양수 무한대로 가는 값의 범위를 갖습니다.마치 연속변수 처럼말입니다.

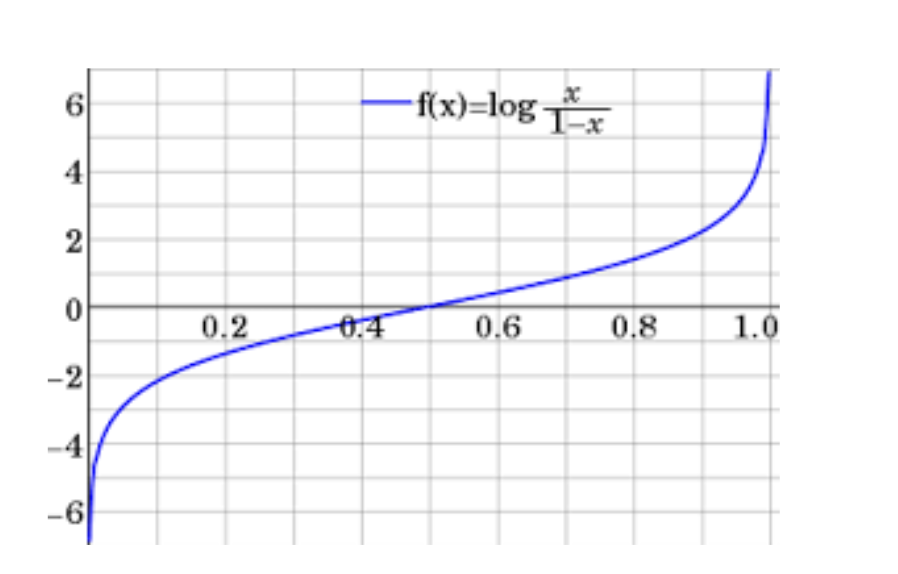
📌 시그모이드(sigmoid)

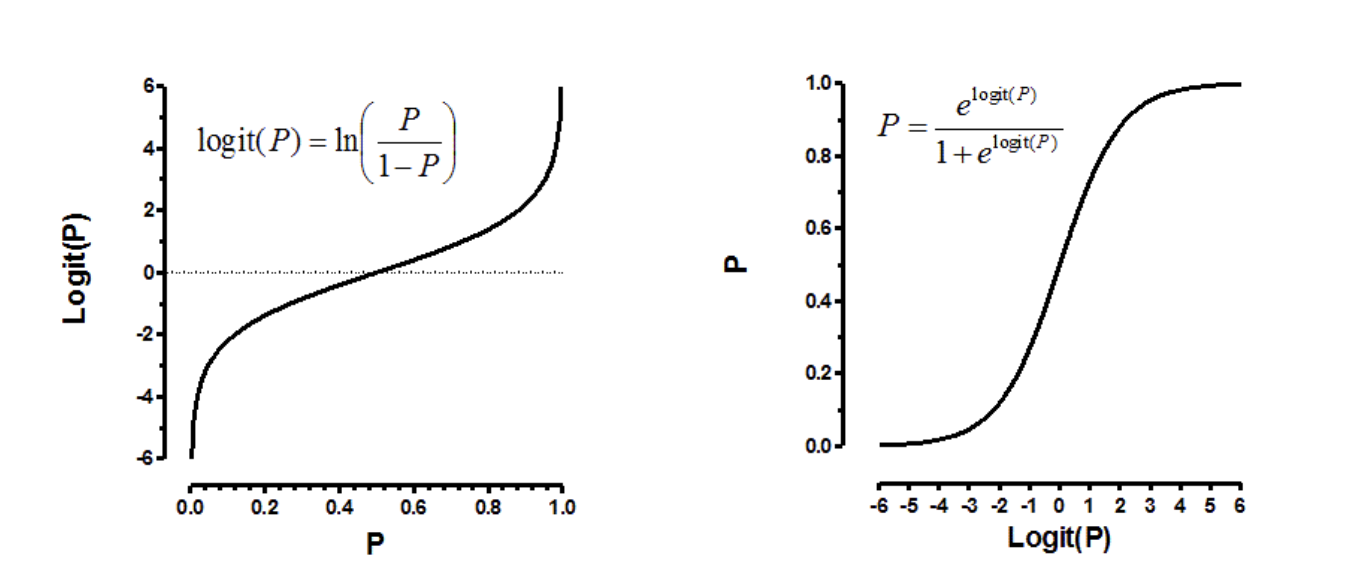
오즈비에 로그를 씌워 로짓으로 만들어 연속 변수처럼 만들었지만 음수무한대에서 양수의 무한대로 가기 때문에 그 자체로 해석하기가 힘듭니다. 이를 위해 시그모이드 함수를 적용하여 확률 값으로 변환합니다.

시그모이드 함수는 S자 모양의 곡선을 가지며, 입력 값이 증가함에 따라 1로 수렴하고, 감소함에 따라 0으로 수렴합니다. 이 함수를 로지스틱 회귀에 적용하면 로짓을 확률 값으로 변환할 수 있습니다. 즉, 로짓 값을 시그모이드 함수에 입력으로 넣으면 [0, 1] 범위의 확률 값이 출력됩니다. 이렇게 변환된 확률 값은 특정 데이터가 특정 범주에 속할 확률을 나타내며, 분류 문제에서 예측 결과로 활용됩니다.

쉽게 말해 로지스틱 회귀에서 시그모이드 함수를 적용하는 이유는 로짓의 값을 [0, 1] 범위의 확률 값으로 변환하여 분류 문제의 예측 결과로 사용하기 위해서입니다.