📌 과적합 문제의 이해

선형 회귀는 데이터 포인트들 사이의 관계를 나타내는 직선을 찾는 모델입니다. 하지만 때로는 데이터가 복잡하거나 과도하게 피팅될 수 있어서 모델이 과적합될 수 있습니다. 이때 regularization은 모델을 개선하고 일반화 능력을 향상시키는 강력한 도구입니다.

과적합(overfitting)은 모델이 훈련 데이터에 지나치게 맞추어져 새로운 데이터에 대한 예측 능력이 떨어지는 상황을 말합니다. 아래 그림을 통해 살펴보겠습니다.

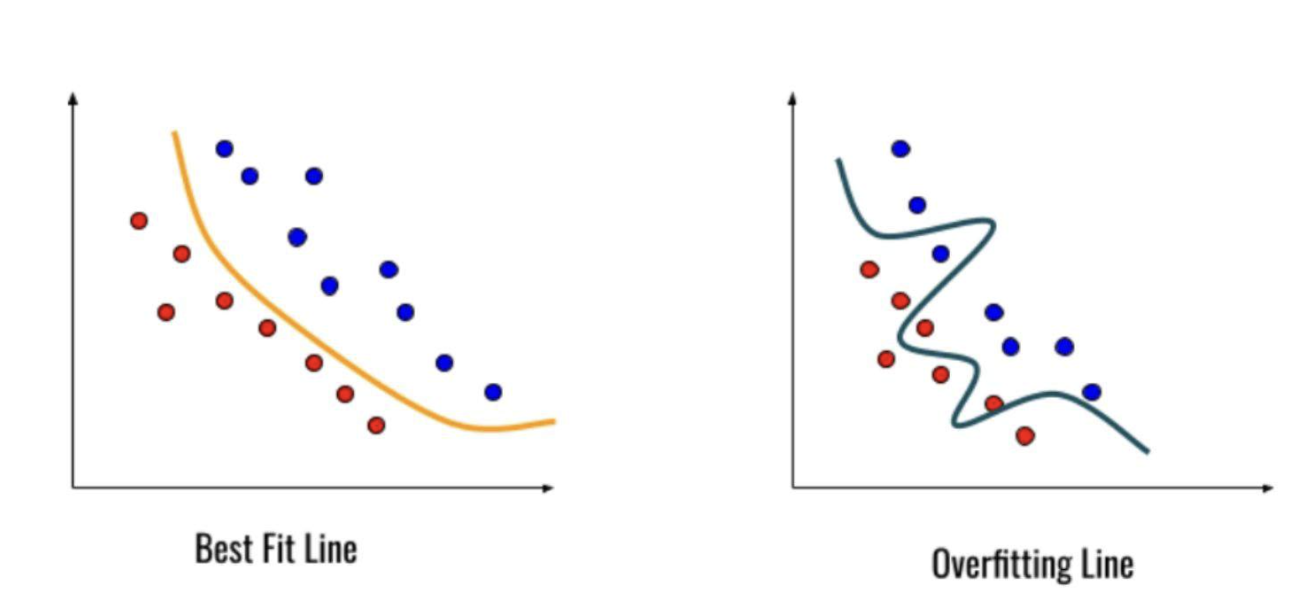
오른쪽 과적합 모델은 새로운 데이터에 대한 예측이 제대로 되고 있지 않는 모습을 보입니다. 이러한 과적합을 완화하기 위해서는 크게 3가지를 고려해볼 수 있습니다.

• Training Data
• Batch Normalization
• Weight Regularization
• Drop-Out

이번 글에서는 Regularization에 대해 설명하도록 하겠습니다!

📌 Regularization의 필요성

학습을 진행할 때, 학습 데이터에 따라 특정 weight의 값이 커지게 되며 이로 인해 과적합이 일어날 가능성이 아주 높습니다. L1 norm , L2 norm을 적용해 을 가져와 학습에 영향을 미치는 cost function을 조정하게 됩니다.

1️⃣ L1 Norm & L2 Norm 이해

Norm은 벡터나 행렬의 크기를 측정하는 방법이며, 일반적으로 벡터의 길이나 크기를 나타내는 지표입니다. 벡터를 공간에서 얼마나 멀리 떨어져 있는지를 측정하는 역할을 합니다. Norm은 수학적으로 다양한 방식으로 정의될 수 있지만, 주로 사용되는 Norm은 L1 Norm과 L2 Norm입니다. L1은 보통 맨해튼 거리법으로, L2는 유클리드 거리법으로 표현됩니다.

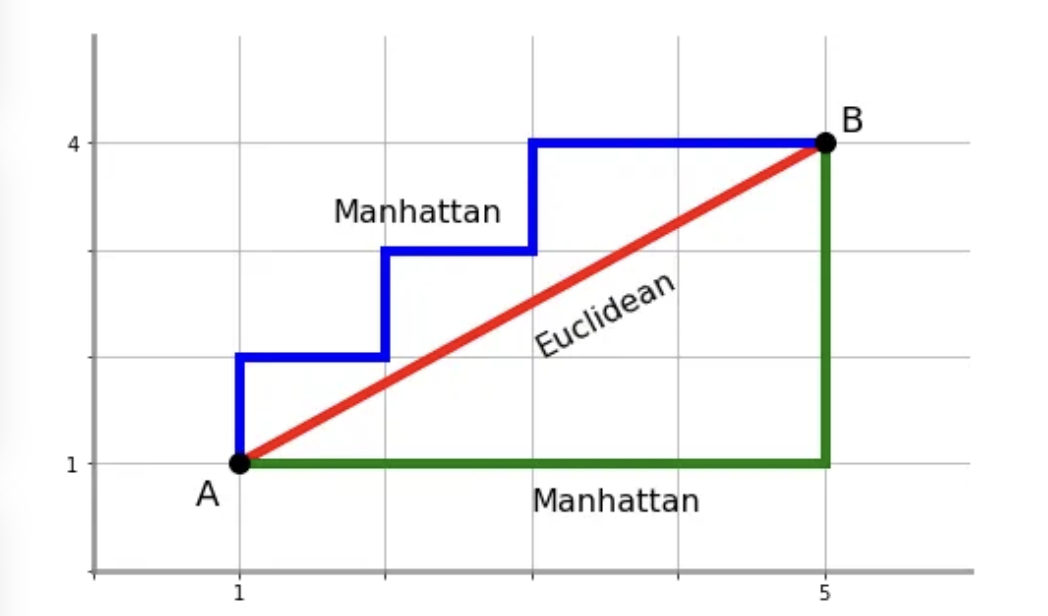
L1 Norm

L1 norm에 의해 도출되는 거리를 L1 distance 또는 Manhattan distance로 표현할 수 있습니다. L1 Norm은 벡터의 각 원소의 절대값을 모두 더한 것을 의미합니다.

$\|x\|_1 = |x_1| + |x_2| + \ldots + |x_n|$

L1 Norm의 특징은 각 원소의 절대값의 합으로 표현되기 때문에, 벡터 공간에서 각 원소가 축에 대해 얼마나 떨어져 있는지를 계산합니다. L1 Norm은 변수의 선택이나 피처 선택을 강조하고, 일부 원소를 0으로 만들어 차원을 축소하는 효과를 가지며, 이는 변수 간의 상대적인 영향력을 다루기에 유용합니다.

L2 Norm

L2 Norm은 벡터의 각 원소의 제곱을 모두 더한 후, 그 제곱근을 구한 것을 의미합니다. Euclidean distance로도 알려져 있습니다.

$\|x\|_2 = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}$

L2 Norm의 특징은 각 원소의 제곱의 합의 제곱근으로 표현되기 때문에, 벡터 공간에서 원점(0, 0)으로부터 얼마나 떨어져 있는지를 계산합니다. L2 Norm은 변수들의 영향력을 골고루 분산시키며, 가중치들이 작은 값으로 편향되는 경향을 가집니다.

2️⃣ L1 규제(Lasso) & L2 규제(Ridge) 이해

모델을 학습시킨다는 것은 모델의 가중치(Weight)를 조정하여 입력 데이터와 관련된 패턴을 학습하는 것을 의미합니다. 그러나 때로는 모델의 가중치 중 일부가 학습 과정에서 과도하게 커지는 현상이 발생할 수 있습니다. 이러한 상황에서는 해당 가중치가 특정 입력에 극단적으로 의존하게 되어 모델의 예측이 불안정해지고, 일반화 능력이 저하될 수 있습니다.
이러한 문제를 해결하기 위해 L1 Norm, L2 Norm의 컨셉을 가지고와 L1 및 L2 규제를 하게됩니다. 다르게 표현해 규제를 하게되면 가중치에 "락(Lock)"을 거는 역할을 합니다. 즉, 네트워크가 어떤 특성에 지나치게 의존하지 않도록 하며, 모델이 더 일반화된 특징을 학습하도록 유도합니다.

L1 규제 (Lasso)

L1 규제ㅈ는 모델의 가중치에 절댓값을 적용한 뒤, 이 값을 최소화하도록 하는 방식입니다. 이로 인해 일부 가중치가 0이 되거나 0에 가까워집니다. 즉, Lasso는 예측에 중요하지 않은 변수의 회귀계수를 감소시킴으로써 변수선택(Feature Selection)하는 효과를 냅니다.

$Loss_L1 = Original_Loss + λ * ∑(|w_i|)$

• L1 e는 원래의 손실 함수에 가중치의 절댓값 합을 추가합니다. 이로 인해 가중치가 작아지도록 유도합니다.
• 모델을 편미분하여 가중치에 대한 최적값을 구하게 되면, 가중치 값이 상수로 대체됩니다. 따라서 이때 가중치의 부호에 따라 최적값이 양수 혹은 음수가 결정됩니다.
• 가중치가 너무 작아지게 되면, 가중치에 곱해지는 상수 또한 작아지게 됩니다. 이에 따라 가중치가 0에 가까워질 가능성이 높아집니다.
• 결과적으로 L1 규제화는 일부 중요한 가중치만을 남기고 나머지는 0으로 만들어 모델의 특성 선택을 유도합니다. 중요한 특성만을 활용하는 sparse한 모델을 생성하게 됩니다.

L2 규제 (Ridge)

L2 규제화는 모델의 가중치에 제곱을 적용한 뒤, 이 값을 최소화하도록 하는 방식입니다. L2 규제화는 가중치의 크기를 작게 유지하여 모델이 데이터에 덜 민감하게 반응하도록 합니다.

$Loss_L2 = Original_Loss + λ * ∑(w_i^2)$

• L2 규제화는 원래의 손실 함수에 가중치의 제곱 합을 추가합니다. 이로 인해 가중치가 작아지도록 유도합니다.
• 모델을 편미분하여 가중치에 대한 최적값을 구하게 되면, 가중치 값이 상수로 대체됩니다. 이때 가중치 값의 크기와 부호 모두에 의해 최적값이 결정됩니다.
• 가중치가 작아지면, 가중치에 곱해지는 상수 또한 작아지게 됩니다. L2 규제화는 가중치가 0으로 수렴하지는 않지만, 크기를 제한하여 가중치가 작게 유지됩니다.
• L2 규제화는 모델의 가중치들을 고르게 분포시켜 모델이 모든 특성을 중요하게 고려하도록 돕습니다.

---

참고

• https://huidea.tistory.com/154
• https://hwanii-with.tistory.com/58
• https://junklee.tistory.com/29