[ML] 선형 회귀 (Linear Regression)

선형 회귀란?

머신러닝의 말 그대로 기계를 학습시켜 답을 구하는 것이라고 할 수 있습니다
그래서 어떤 값을 넣었을 때 발생할 수 결과 값을 예측할 수 있습니다.

이때 우리가 가장 직관적이고 간단하게 결과값을 구하는 방법은 선입니다.
중학교 수학시간에 배운 직선 그래프를 생각해본다면, y= ax+b로 표현하죠.
이때 x값에 값을 넣으면 y값을 구할 수 있는 원리 처럼 선형회귀 또한 실제 데이터를 가장 잘 예측할 수 있는 최적의 a(기울기), b(절편)를 구하는 겁니다!

잘 예측하는 선형회귀란?

어떤 모델이 잘 예측한다고 말할 수 있을까요?
실제 값과 예측 값의 차이가 적은 모델이라고 할 수 있을 겁니다.

이해를 돕기 위해서 예시를 들어서 설명해 보도록 할께!
우선 x축을 키,y축은 몸무게로 산점도 그래프를 만들어보세요.

import matplotlib.pyplot as plt

height1 = [160, 165, 174]
weight1 = [67, 70, 87]

plt.scatter(height1, weight1)
plt.ylabel('weights')
plt.xlabel('heights')
plt.axis([155, 175, 50, 90])
plt.show()코드를 입력하세요

그럼 아래와 같이 그래프가 나오게 됩니다.

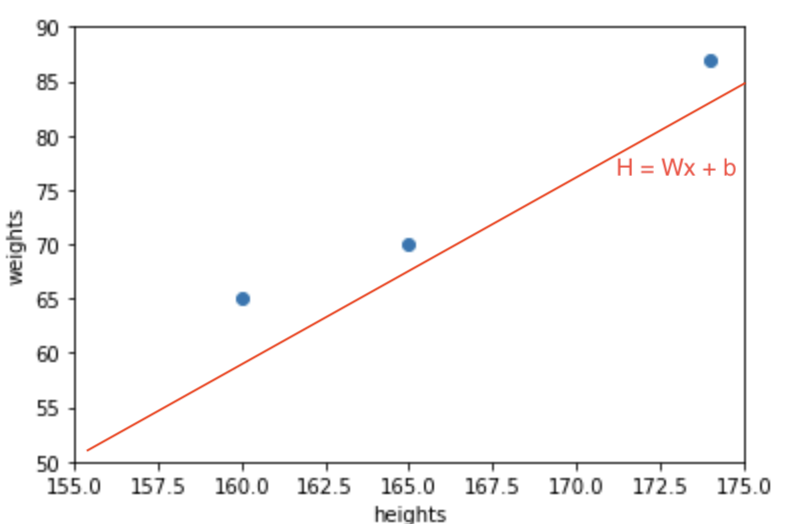
빨간색은 초기 예측 그래프이며, 파란색 점은 실제 데이터 값을 의미합니다.
저희가 빨간색선의 기울기와 y절편을 조정하며 파란색 선을 맞춰나가야만 더 좋은 예측 모델을 만들수 있을 겁니다.

우선 초기모델이 실제 그래프와 얼마나 다른지 확인할 필요가 있습니다.
3개의 점은 예측그래프와 각각 3,1,2가 차이 난다고 가정해봅시다.
각 차이를 제곱하여 3으로 나눈다면 $\frac{14}{3}$ 라는 결과를 가지게 됩니다.
이 값이 클수록 예측그래프의 값(W,b)이 많이 잘못됐음을 의미합니다.
이처럼 목표와 가설의 차이를 계산하는 것을 비용함수라고 하며, 최소제곱법을 사용하게 되는 것입니다.
비용함수는 아래와 같습니다

$Cost(w,b) = \frac{1}{m} \times \sum_{i=1}^{m} (wx_i+b -y_i)^2$

선형회귀의 비용을 줄일 수 있는 방법은?

선형 회귀의 초기 모델의 비용를 알았다면 이를 서서히 줄여나가는 것이 과제될 것입니다.
오차를 줄이는 방법은 다양하지만 이중 가장 많이 사용하는 "경사하강법" 을 알려드리도록 하겠습니다.

$Cost(w,b) = \frac{1}{m} \times \sum_{i=1}^{m} (wx_i+b -y_i)^2$

비용의 함수에서 w와 b에 대하여 편미분을 해야합니다:

w기울기 = $\frac{\partial cost(w,b)}{\partial w}= \frac{1}{m} \times \sum_{i=1}^{m} (2(x_i)^2w+2x_ib-2x_iy_i)$
b기울기 = $\frac{\partial cost(w,b)}{\partial b}= \frac{1}{m} \times \sum_{i=1}^{m} (2x_iw-2y_i+2b)$

이렇게 구해진 편미분 값을 초기의 w,b 값에 빼주며 기울기와 절편을 조정해줍니다.
$w: = w - \alpha(\frac{\partial cost(w,b)}{\partial w})$
$b: = b - \alpha(\frac{\partial cost(w,b)}{\partial b})$
이때 각 편미분의 기울기가 크기 때문에 $\alpha$를 곱하여 그 크기를 줄여주게 됩니다. 이러한 $\alpha$를 "learning rate" 를 라고 부릅니다.

이러한 과정을 통해 예측모델을 조정하게 되는데, 이를 "epoch" 라고 부르게됩니다.