군집화란?
이미 일상 속에서 군집화의 개념을 사용하고 있습니다.
비슷한 사람끼리 잘 어울리는 걸보면 "유유상종", "끼리끼리 사이언스" 등이라고 말하죠?
이처럼 비슷한 데이터끼리 묶어 그룹을 만드는 것을 "군집화"라고 부릅니다.
말이 어렵지, 데이터들이 속할 그룹을 지정해주는 거라고 생각하시면 됩니다 ㅎㅎ
군집화를 잘한다는 건 어떤 의미지?
군집화를 잘했다는 건 그룹내, 그룹외의 두가지 관점으로 볼수 있어요!
- 그룹 간에 특징이 서로 상이하다
- 그룹 내 데이터들이 서로 유사하다
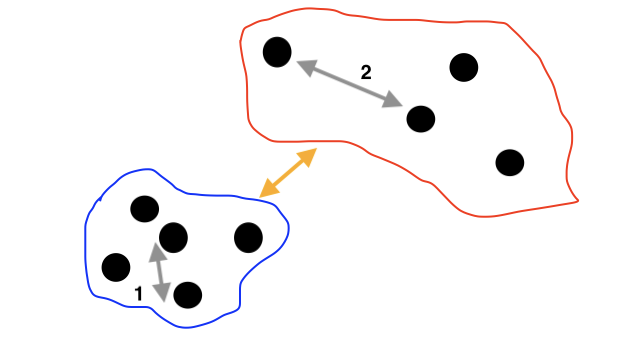
파란색과 빨간색으로 군집화를 시켰다고 가정하면 위와 같은 이미지처럼 보이겠죠.
1. 그룹 간에 특징이 서로 상이하다
파란색과 빨간색이 너무 가깝지도 않고 겹치지도 않으니 각 그룹은 서로 확실히 다름을 알수 있습니다.
2. 그룹 내 데이터들이 서로 유사하다
그룹별로 더 자세히 들여다 보면 그룹내 데이터 점 사이의 거리를 확인할 수 있습니다.
1번은 2번선의 길이 보다 짧은 걸 보아 1번 데이터들은 2번 그룹보다서로 유사하다고 말할수 있어요!
군집화를 어떤 방법으로 하면 될까?
군집화를 하는데 여러 방법이 있지만, 제목에 적어둔 대로 K-Means와 Hierarchical clustering(계층적 군집화)에 대해서만 정리하도록 하겠습니다.
1. K-Means
K-Means라는 군집화 방법이 어떻게 흘러가는지 step by step으로 이미지와 함께 설명드리도록 할께요.
1) 우선 K의 갯수를 정해주세요
우선 K-Means의 K는 저희가 넣을 수 있는 숫자를 의미합니다.
저는 3이라고 가정해볼께요!

3이라는 갯수만큼 가상의 포인트가 생기게 됩니다.
여기서 주목 해야하는건 가상의 포인트를 만들기에 real random으로 찍히게 됩니다!
2) 데이터와 가상의 포인트의 거리를 계산하여, 어떤 가상의 포인트와 가까운지 확인하고 이를 그룹화합니다.
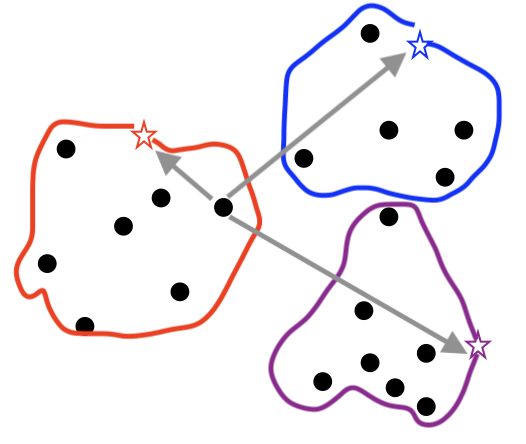
한 점을 꼭 집어서 말씀드리면, 한점에서 각 색깔별 가상의 점의 길이를 구하게 됩니다.
눈으로 보니 빨간색 점과 가장 가까워 보이네요. (사실 데이터는 너무너무 가까운 경우도 많아요. 하지만이해를 돕기위해 엄청 확대 했다고 생각해보세요~)
그러면 그 점은 빨간색 그룹에 속하게 됩니다.
이를 모든 점에 대해 실행하게 되면 아래와 같은 군집이 만들어집니다.
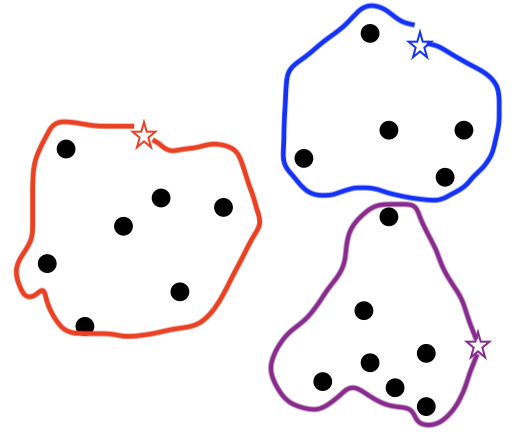
3) 그룹별 중심점을 찾아서, 여전히 데이터들이 새로운 중심점과 가까운지 확인합니다.
가상의 점 --> 군집의 중심점으로 옮기게 됩니다.
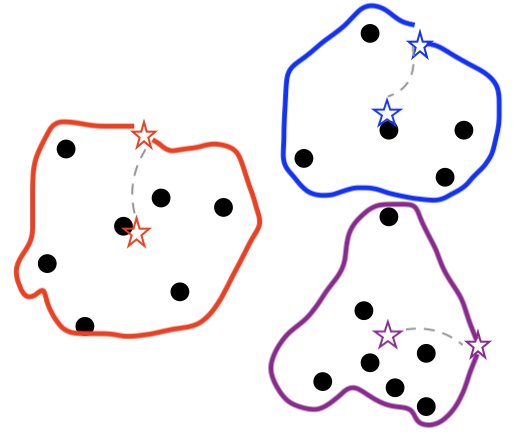
그리고 2번과 같이 데이터점과 3개의 점사이의 거리를 계산하게 됩니다.
만약 다른 군집의 중심점과 더 가깝다면 군집의 모양이 변경됩니다.
한점은 초기에는 보라색 그룹에 속했으나, 중심점으로 기준을 옮기니 파란색 그룹에 가깝게 되었습니다.
그래서 군집의 모양이 바뀌게 되었습니다.
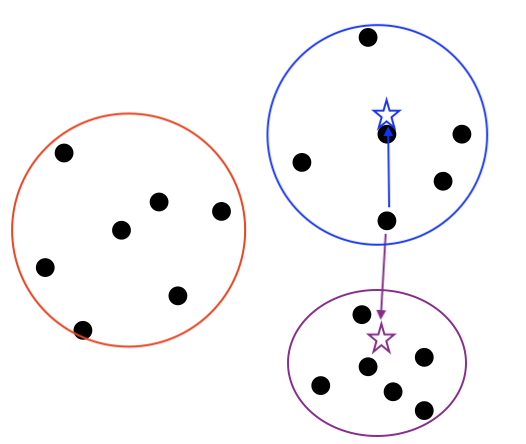
4) 군집의 중심이 변경이 없을 때 까지 2-3번 과정을 반복해주세요.
2. Hierarchical clustering (계층적 군집화)
To be continued...
쉬운 설명으로 다시 돌아올께요 ㅎㅎ